700. 二叉搜索树中的搜索">700. 二叉搜索树中的搜索
98. 验证二叉搜索树">98. 验证二叉搜索树
530. 二叉搜索树的最小绝对差">530. 二叉搜索树的最小绝对差
501. 二叉搜索树中的众数">501. 二叉搜索树中的众数
- 思路一：当成普通二叉树来处理
- 思路二：
236. 二叉树的最近公共祖先">236. 二叉树的最近公共祖先
- 思路：用后序遍历遍历整根树
235. 二叉搜索树的最近公共祖先">235. 二叉搜索树的最近公共祖先
- 按照一般的二叉树处理
- 利用二叉搜索树的性质
  - 递归
  - 迭代
701. 二叉搜索树中的插入操作">701. 二叉搜索树中的插入操作
- 递归
  - 带返回值的递归函数
  - 不带返回值的递归函数
- 迭代
450. 删除二叉搜索树中的节点">450. 删除二叉搜索树中的节点
- 递归
- 迭代
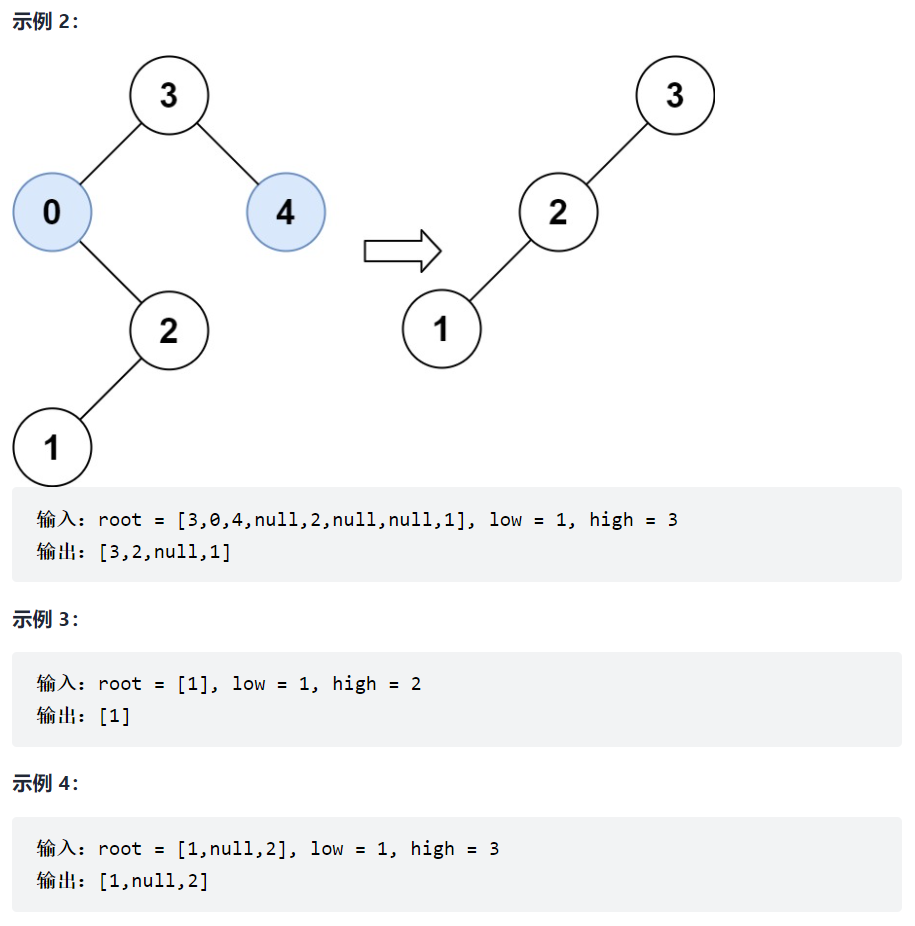
669. 修剪二叉搜索树">669. 修剪二叉搜索树
- 递归
- 迭代法
108. 将有序数组转换为二叉搜索树">108. 将有序数组转换为二叉搜索树
- 递归
- 迭代
1382. 将二叉搜索树变平衡">1382. 将二叉搜索树变平衡
538. 把二叉搜索树转换为累加树">538. 把二叉搜索树转换为累加树
- 递归
- 迭代法

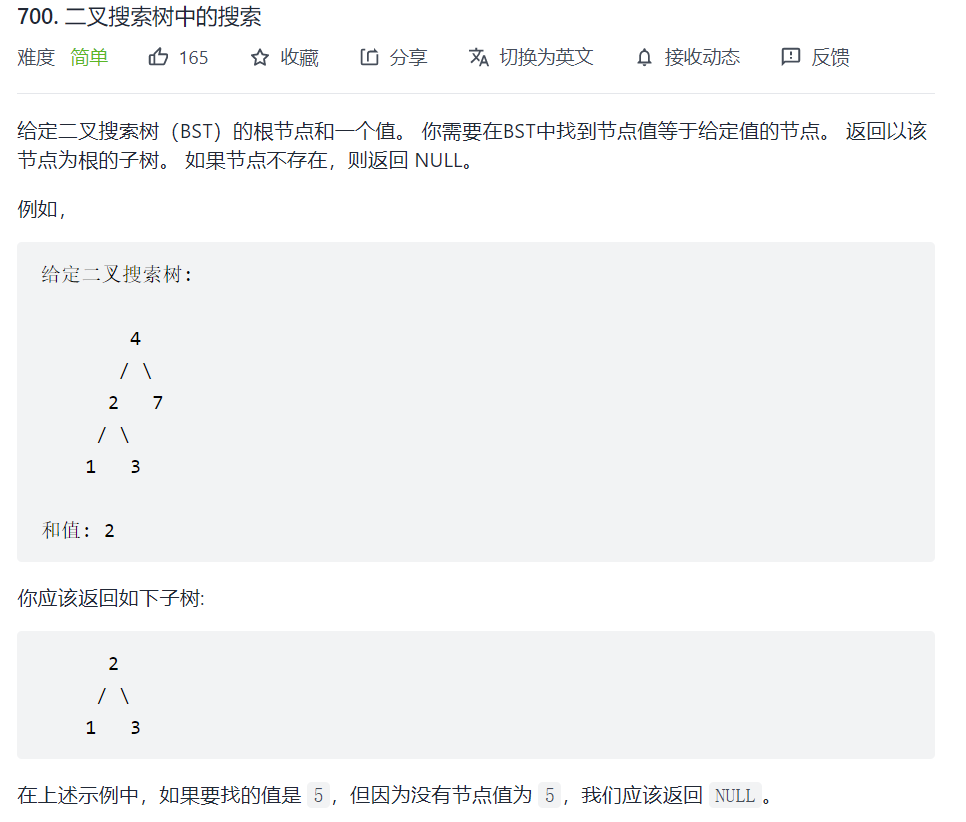
700. 二叉搜索树中的搜索

递归法

递归的参数和返回值

返回root->val == val的子树，因此，返回值为TreeNode*
参数为节点和val

递归终止条件

当节点为空时，返回nullptr

单层递归的逻辑

二叉搜索树就是比当前节点大的点在右子树上，比它小的点在左子树上，因此：

如果当前节点值大于val，递归处理左子树
如果当前节点值小于val，递归处理右子树
如果相等，返回当前节点

完整代码：

class Solution {
public:
    TreeNode* searchBST(TreeNode* root, int val) {
        if (!root) return nullptr;
        if (root->val > val) return searchBST(root->left, val);
        else if (root->val < val) return searchBST(root->right, val);
        return root;
    }
};

迭代法

这道题用迭代法可能更好一些，甚至不需要用额外的存储空间
思路：

如果当前节点值大于val，对比左孩子
如果当前节点值小于val，对比右孩子
如果相等，返回当前节点
最后没找到的话，返回nullptr

class Solution {
public:
    TreeNode* searchBST(TreeNode* root, int val) {
        while (root) {
            if (root->val > val) root = root->left;
            else if (root->val < val) root = root->right;
            else return root;
        }
        return nullptr;
    }
};

总结

其实这就是个二分查找
时间复杂度为log，最坏为N

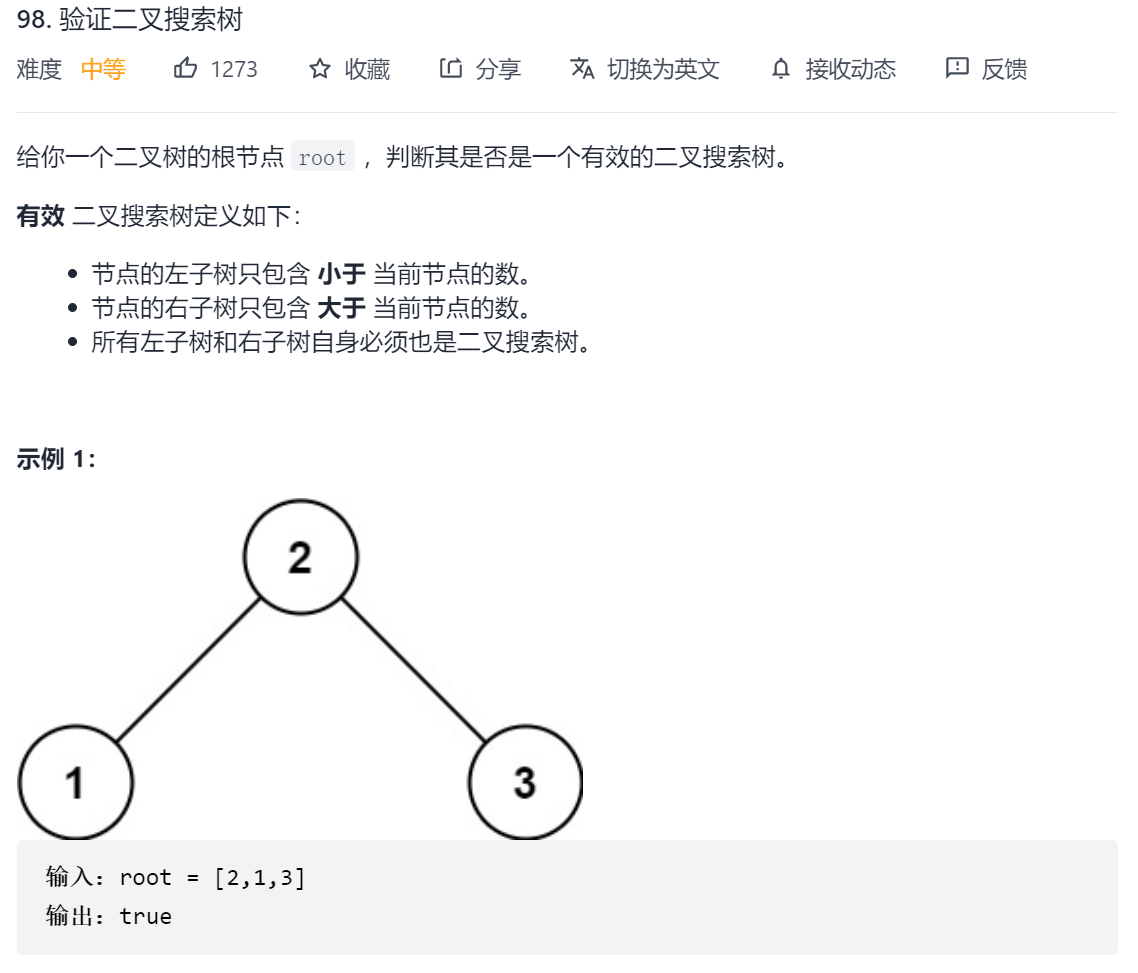
98. 验证二叉搜索树

陷阱

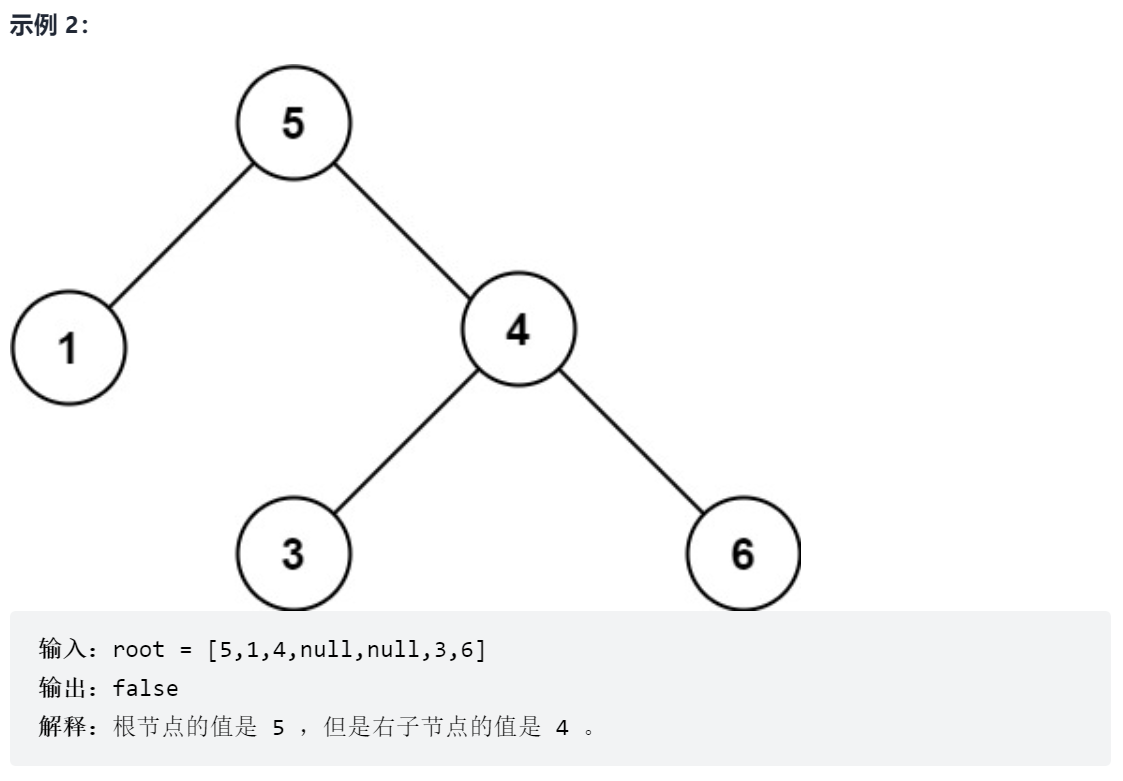
陷阱一：不能单纯的比较根结点和左右子节点，因为搜索树要求子树的所有节点都必须满足大于或小于根结点，比如下面这个树

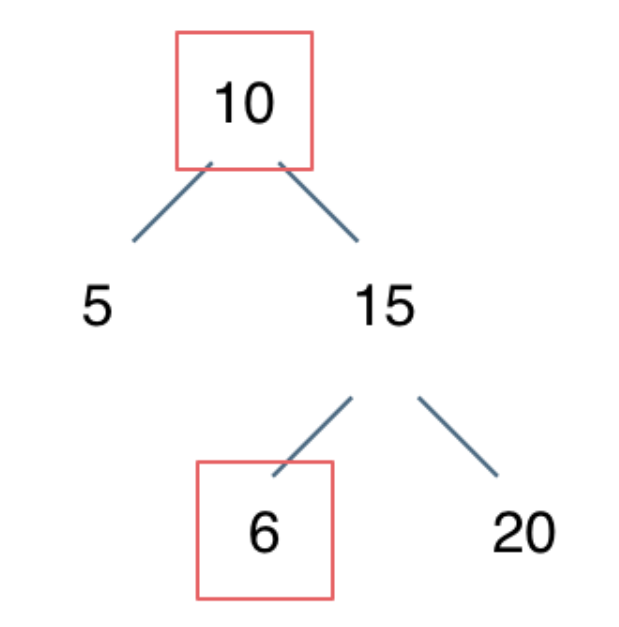
陷阱二：样例中最小节点可能是int的最小值，如果这样使用最小的int来比较也是不行的。此时可以初始化比较元素为longlong的最小值。问题可以进一步演进：如果样例中根节点的val 可能是longlong的最小值又要怎么办呢？

最开始提交的代码就是犯了直接比较节点的错误，结果一直提交都没通过

class Solution {
public:
    bool isValidBST(TreeNode* root) {
        if (!root) return true;
        if (!root->left && !root->right) return true;
        if (root->left && root->left->val >= root->val)
            return false;
        if (root->right && root->right->val <= root->val)
            return false;

        return isValidBST(root->left) && isValidBST(root->right);

    }
};

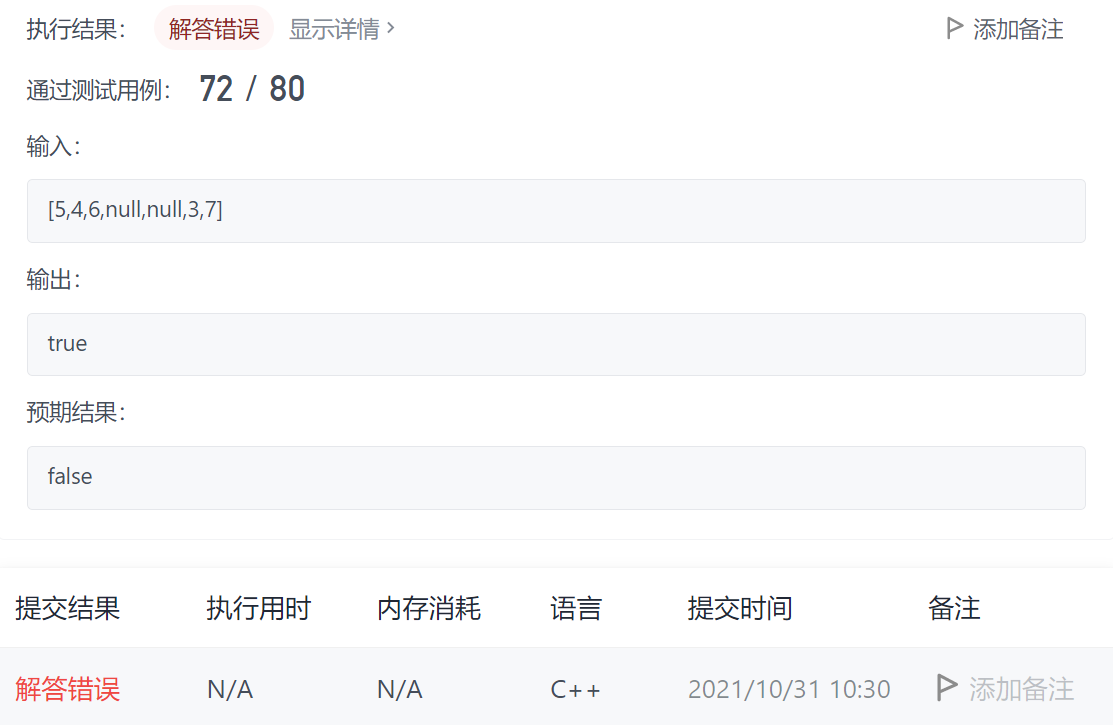
下面看一下正确思路

思路一

二叉搜索树如果中序遍历得到一个数组的话，这个数组一定是有序（单调递增）的，那么我们把它转化为数组，再判断是否有序好了

class Solution {
public:
    void inTraversal(TreeNode* root, vector<int>& nums) {
        if (!root) return;
        inTraversal(root->left, nums);
        nums.push_back(root->val);
        inTraversal(root->right, nums);
    }
    bool isValidBST(TreeNode* root) {
        vector<int> nums;
        inTraversal(root, nums);

        for (int i = 0; i < nums.size() - 1; i++) {
            if (nums[i] >= nums[i + 1]) // 二叉树不能有重复元素，严格单调，所以要加等号
                return false;
        }
        return true;
    }
};

终于通过了，泪目了！

思路二

在递归的过程中直接判断是否有序，不需要额外数组

确定参数和返回值

返回类型为bool，参数是节点

终止条件

如果节点为空，返回true

单层递归逻辑中序

搜索树中序遍历的结果为递增的，因此采用中序遍历的方法来处理

首先递归处理左子树
然后比较当前节点的值和保存的最大值：
- 如果当前节点的值大于maxValue，更新maxValue
- 否则，说明左子树中有节点大于当前节点，返回false
递归处理右子树

因为测试样例中有int的最小值，所以用long long类型的最小值记为初值

class Solution {
public:
    long long maxVal = LONG_MIN; // 因为后台测试数据中有int最小值
    bool isValidBST(TreeNode* root) {
        if (!root) return true;
        bool left = isValidBST(root->left);

        if (maxVal < root->val) maxVal = root->val;
        else return false;

        bool right = isValidBST(root->right);
        return left && right;
    }
};

如果想要避免使用long long类型，可以通过记录前一个节点的方式来比较节点的值

class Solution {
public:
    TreeNode* pre;
    // 如果当前访问节点小于等于前一个节点时，return false
    bool isValidBST(TreeNode* cur) {
        if (cur == nullptr) return true;
        bool left = isValidBST(cur->left);
        if (!left) return false; // 剪枝
        if (pre != nullptr && cur->val <= pre->val) {
            return false;
        }
        pre = cur;
        bool right = isValidBST(cur->right);
        return right && left;
    }
};

思路三迭代

可以用栈来模拟树的中序遍历，然后在处理根结点的时候进行值的对比

class Solution {
public:

    // 如果当前访问节点小于等于前一个节点时，return false
    bool isValidBST(TreeNode* root) {
        if (root == nullptr) return true;
        TreeNode* pre = nullptr;
        TreeNode* cur = root;
        stack<TreeNode*> st;
        while (cur != nullptr || !st.empty()) {
            while (cur) {
                st.push(cur);
                cur = cur->left;
            }
            cur = st.top();
            st.pop();
            if (pre != nullptr && cur->val <= pre->val)
                return false;
            pre = cur;
            cur = cur->right;
        }
        return true;
    }
};

530. 二叉搜索树的最小绝对差

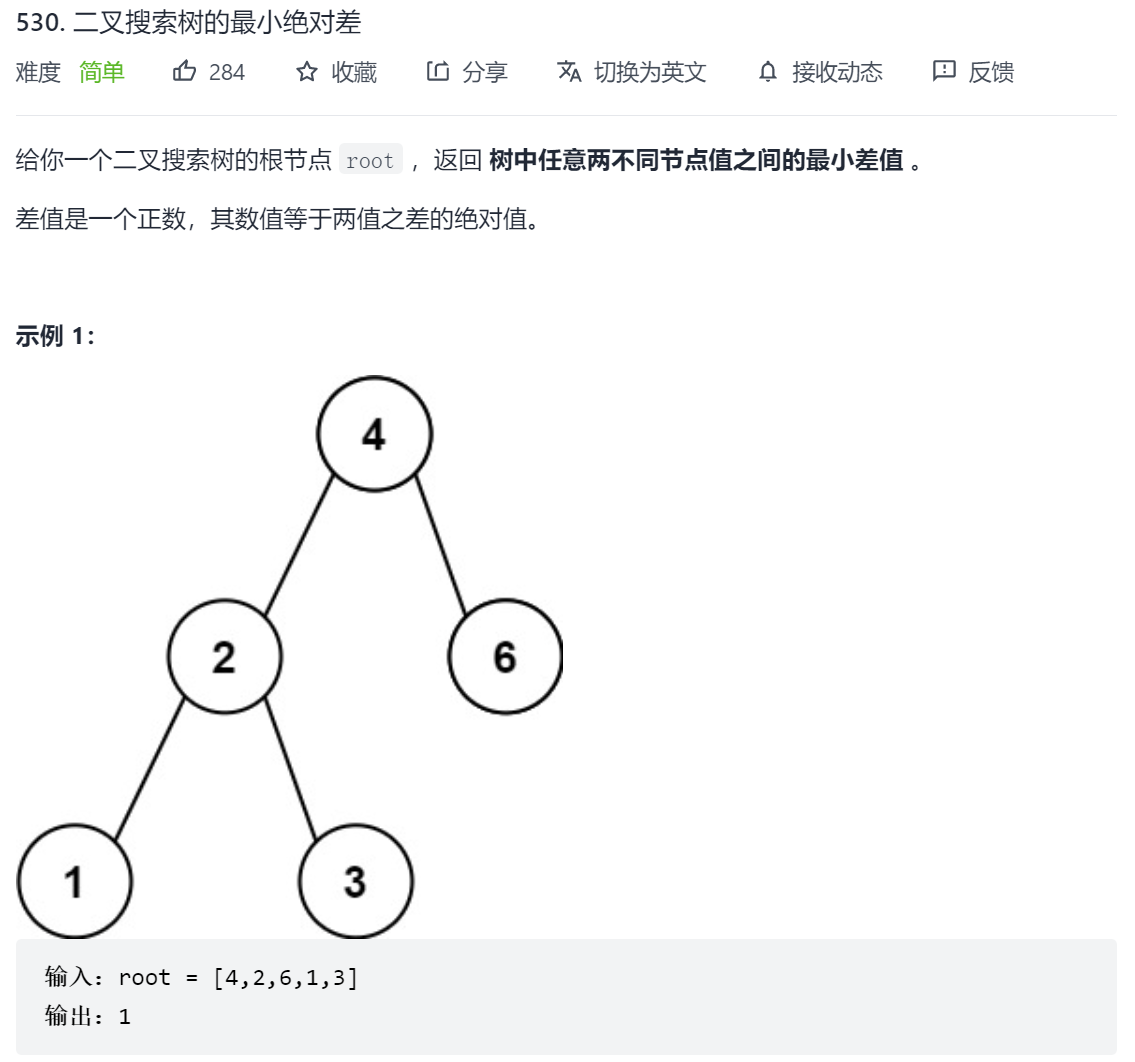
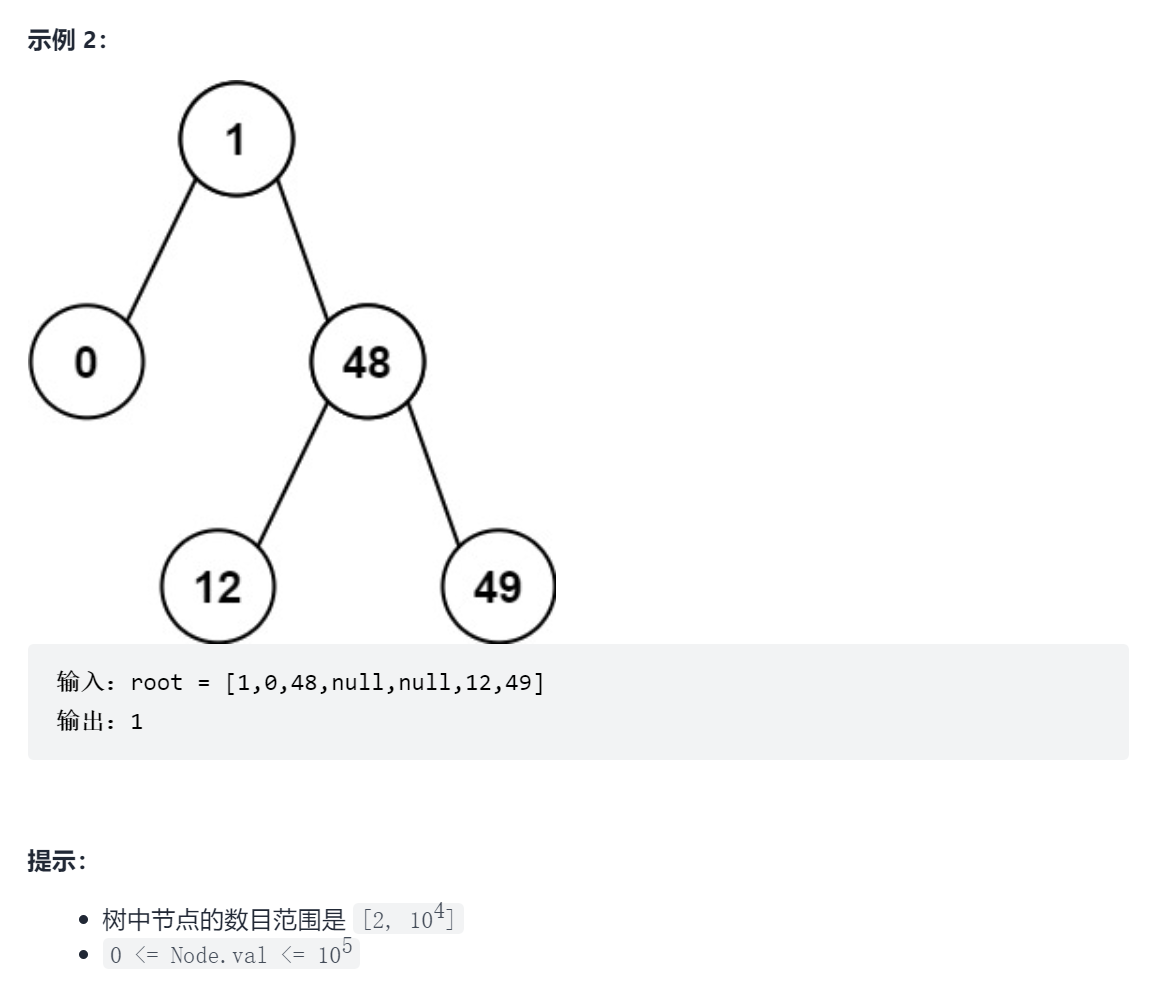
思路一：将树转换为数组

二叉搜索树中序遍历后得到的数组是严格单调的，因此可以先中序遍历得到这个数组，然后从数组中找到最小绝对值之差

因为绝对值之差最下的一定出现在相邻的两个数，只需要遍历一次二叉树，遍历一次数组即可，时间复杂度O(n)

class Solution {
public:
    void traversal(TreeNode* root, vector<int>& nums) {
        if (!root) return;
        traversal(root->left, nums);
        nums.push_back(root->val);
        traversal(root->right, nums);
    }

    int getMinimumDifference(TreeNode* root) {
        vector<int> nums;
        traversal(root, nums);
        int minAbs = INT_MAX;
        for (int i = 1; i < nums.size(); i++) {
            minAbs = min(minAbs, nums[i] - nums[i - 1]);
        }
        return minAbs;
    }
};

思路二：在遍历树的过程中记录差值

其实时有序数组，那么找最小差值只要比较相邻的两个元素就可以了

class Solution {
public:
    TreeNode* pre;
    int res = INT32_MAX;
    void inorder(TreeNode* root) {
        if (root == nullptr) return;
        inorder(root->left);
        if (pre != nullptr) {
            res = min(root->val - pre->val, res);
        }
        pre = root;
        inorder(root->right);
    }

    int getMinimumDifference(TreeNode* root) {
        inorder(root);
        return res;
    }
};

这样将时间复杂度降为O(N)级别

思路三：用栈来模拟中序遍历

class Solution {
public:
    int getMinimumDifference(TreeNode* root) {
        int minAbs = INT_MAX;
        stack<TreeNode*> st;
        TreeNode* cur = root;
        TreeNode* pre = nullptr;
        while (cur || !st.empty()) {
            if (cur) {
                st.push(cur);
                cur = cur->left; // 左
            } else {
                // 中
                cur = st.top(); st.pop();
                if (pre)
                    minAbs = min(minAbs, cur->val - pre->val);
                pre = cur;

                cur = cur->right; // 右
            }
        }
        return minAbs;
    }
};

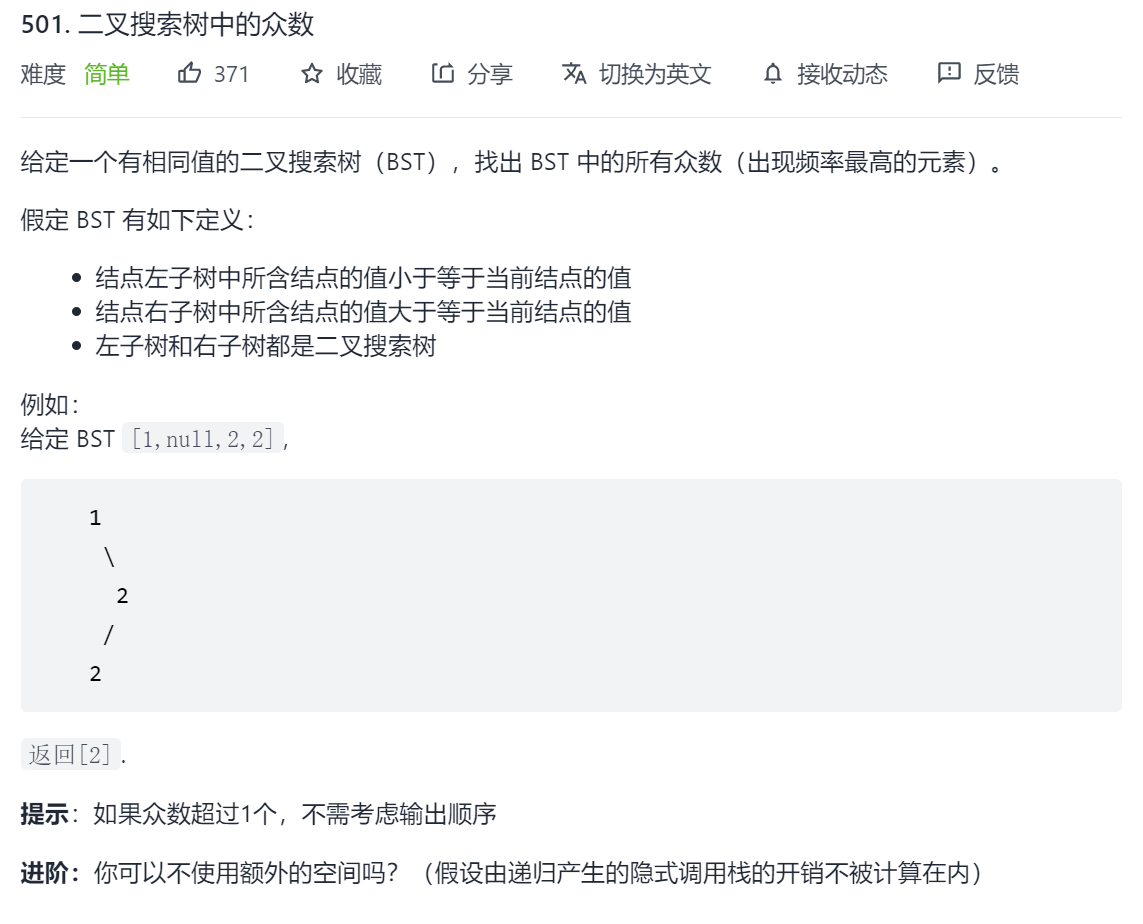
501. 二叉搜索树中的众数

思路一：当成普通二叉树来处理

普通的二叉树，数值位置没有什么规律，因此做法就是遍历整个二叉树，然后用map来统计频率，按频率排序，然后取频率最高的几个

class Solution {
public:
    void traversal(TreeNode* root, unordered_map<int, int>& map) {
        if (!root) return;
        map[root->val]++;
        traversal(root->left, map);
        traversal(root->right, map);
    }

    vector<int> findMode(TreeNode* root) {
        unordered_map<int, int> map;
        traversal(root, map);
        // 先把map转化为vector再排序
        vector<pair<int, int>> vec(map.begin(), map.end());
        // 用lambda，让元素按照second降序
        sort(vec.begin(), vec.end(), [](const pair<int, int>& a, const pair<int, int>& b)->bool{
            return a.second > b.second;
        });
        vector<int> res;
        res.push_back(vec[0].first);
        for(int i = 1; i < vec.size(); i++) {
            if (vec[i].second == vec[0].second)
                res.push_back(vec[i].first);
            else break;
        }
        return res;
    }
};

思路二：

转化为数组处理

class Solution {
public:
    void traversal(TreeNode* root, vector<int>& nums) {
        if (!root) return;
        traversal(root->left, nums);
        nums.push_back(root->val);
        traversal(root->right, nums);
    }

    vector<int> findMode(TreeNode* root) {
        vector<int> nums, res;
        traversal(root, nums);
        int count = 1, maxCount = 1;
        res.push_back(nums[0]);
        for(int i = 1; i < nums.size(); i++) {
            if (nums[i] == nums[i - 1]) {
                count++;
            } else {
                count = 1;
            }
            if (count == maxCount) { // 如果计数和最大一样，那么记录该值
                res.push_back(nums[i]);
            }
            if (count > maxCount) { // 如果大于maxCount，那么清空res，然后记录该值
                maxCount = count;
                res.clear();
                res.push_back(nums[i]);
            }
        }

        return res;
    }
};

直接在中序遍历中进行统计

和前面的题一样，需要用一个指针来记录访问的前一个节点

class Solution {
public:
    int count, maxCount;
    vector<int> res;
    TreeNode* pre;
    void inorder(TreeNode* cur) {
        if (!cur) return;
        inorder(cur->left);
        if (pre && cur->val == pre->val) {
            ++count;
        } else {
            count = 1;
        }

        if (count == maxCount) {
            res.push_back(cur->val);
        } else if (count > maxCount) {
            maxCount = count;
            res.clear();
            res.push_back(cur->val);
        }
        pre = cur;
        inorder(cur->right);
    }

    vector<int> findMode(TreeNode* root) {
        count = 1;
        maxCount = 1;
        inorder(root);
        return res;
    }
};

用栈来模拟中序遍历的迭代法

套用中序遍历的模板，处理中间结点的逻辑一样，直接复制

class Solution {
public:
    vector<int> findMode(TreeNode* root) {
        int count = 0, maxCount = 0;
        TreeNode* pre = nullptr;
        TreeNode* cur = root;
        stack<TreeNode*> st;
        vector<int> res;

        while (cur || !st.empty()) {
            if (cur) {
                st.push(cur);
                cur = cur->left; // 左
            } else {
                // 中
                cur = st.top(); st.pop();

                if (!pre) {
                    count = 1;
                } else if (pre->val == cur->val) {
                    count++;
                } else {
                    count = 1;
                }
                pre = cur;
                if (count == maxCount) {
                    res.push_back(cur->val);
                }
                if (count > maxCount) {
                    maxCount = count;
                    res.clear();
                    res.push_back(cur->val);
                }
                cur = cur->right; // 右
            }
        }
        return res;
    }
};

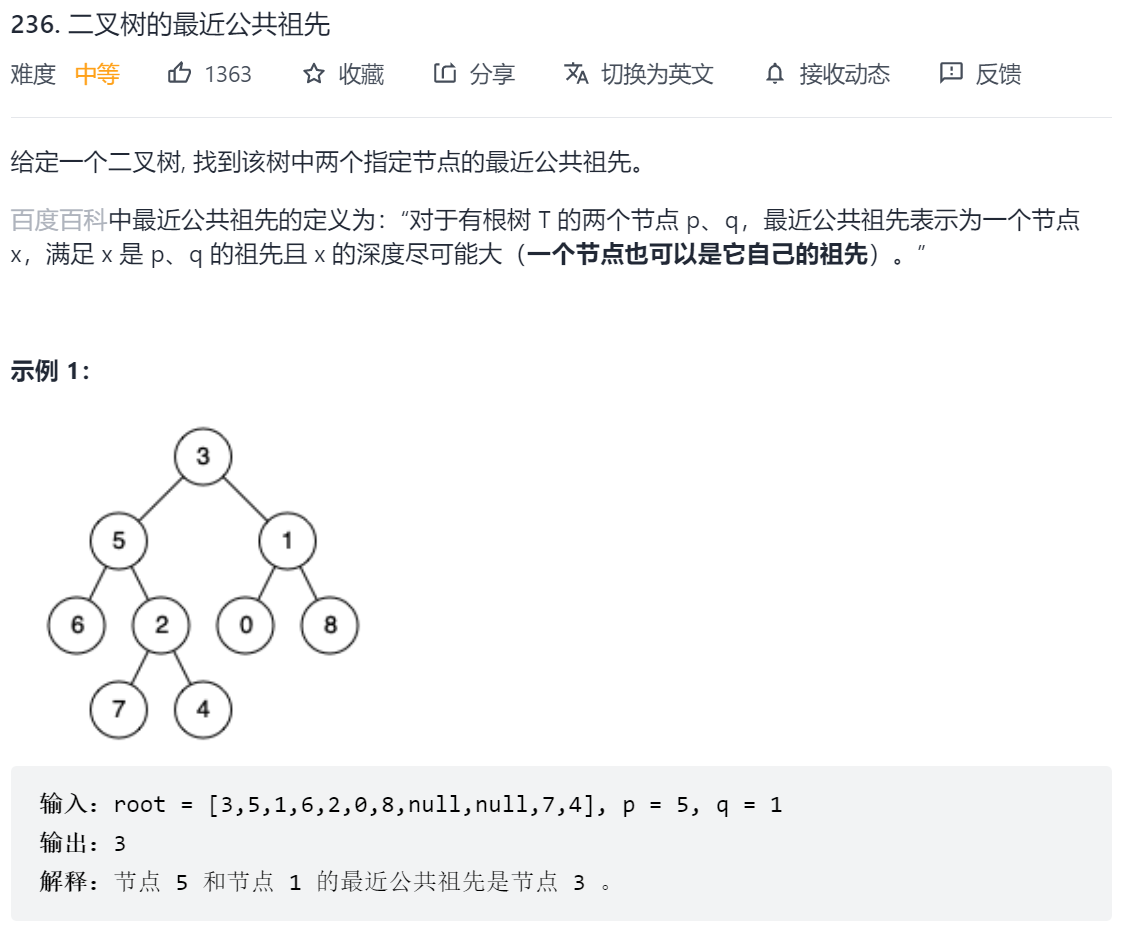
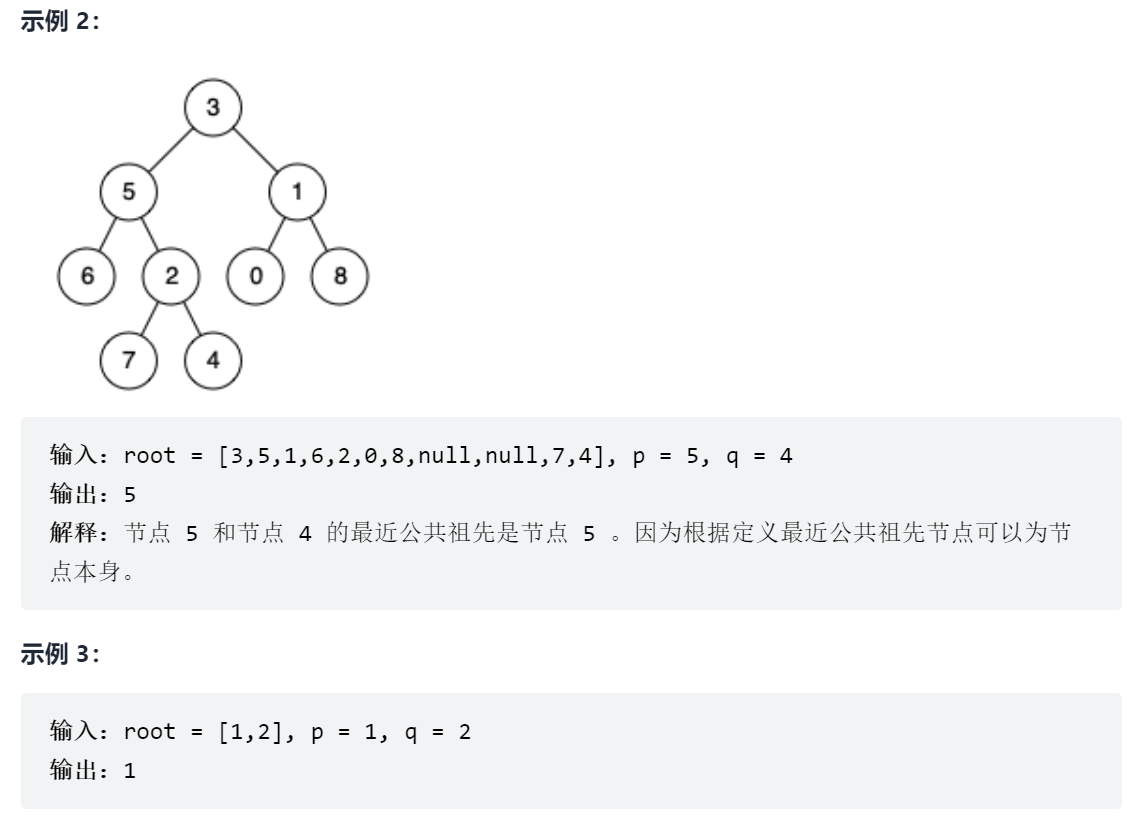
236. 二叉树的最近公共祖先

思路：用后序遍历遍历整根树

这道题找公共祖先，所以要先找到p、q两个节点，然后再向上寻找他们的祖先，也就是需要自底向上遍历整个树。自底向上当然就是回溯了，后序遍历是天然的回溯，本题可以用后序遍历来处理

递归终止条件
如果节点为空，或者找到了p或者q，那么返回当前节点
if (!root || root == p || root == q) return root;

单层递归的逻辑
先用left和right接受递归的返回值，然后判断：

如果right和left都不空，两个都不空，说明一个子树找到了p，一个子树找到了q，那么当前节点就是公共祖先，返回root。
如果right和left有一个空，一个不空，那么返回不空的那一个，表示找到了p、q之一

如果right和left都空，那么返回nullptr

if (right && left) {
  return root;
} else if (left && !right) {
  return left;
} else if (!left && right) {
  return right;
} else {
  return nullptr;
}

完整代码：

class Solution {
public:
  TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
      // 终止条件
      if (!root || root == p || root == q) return root;
      TreeNode* left = lowestCommonAncestor(root->left, p, q);
      TreeNode* right = lowestCommonAncestor(root->right, p, q);
      // 处理left和right的逻辑
      if (right && left) {
          return root;
      } else if (left && !right) {
          return left;
      } else if (!left && right) {
          return right;
      } else {
          return nullptr;
      }
  }
};

精简后：

class Solution {
public:
  TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
      // 终止条件
      if (!root || root == p || root == q) return root;

      TreeNode* left = lowestCommonAncestor(root->left, p, q);
      TreeNode* right = lowestCommonAncestor(root->right, p, q);

      // 处理left和right的逻辑
      if (left && right) return root;
      if (!left) return right;
      return left;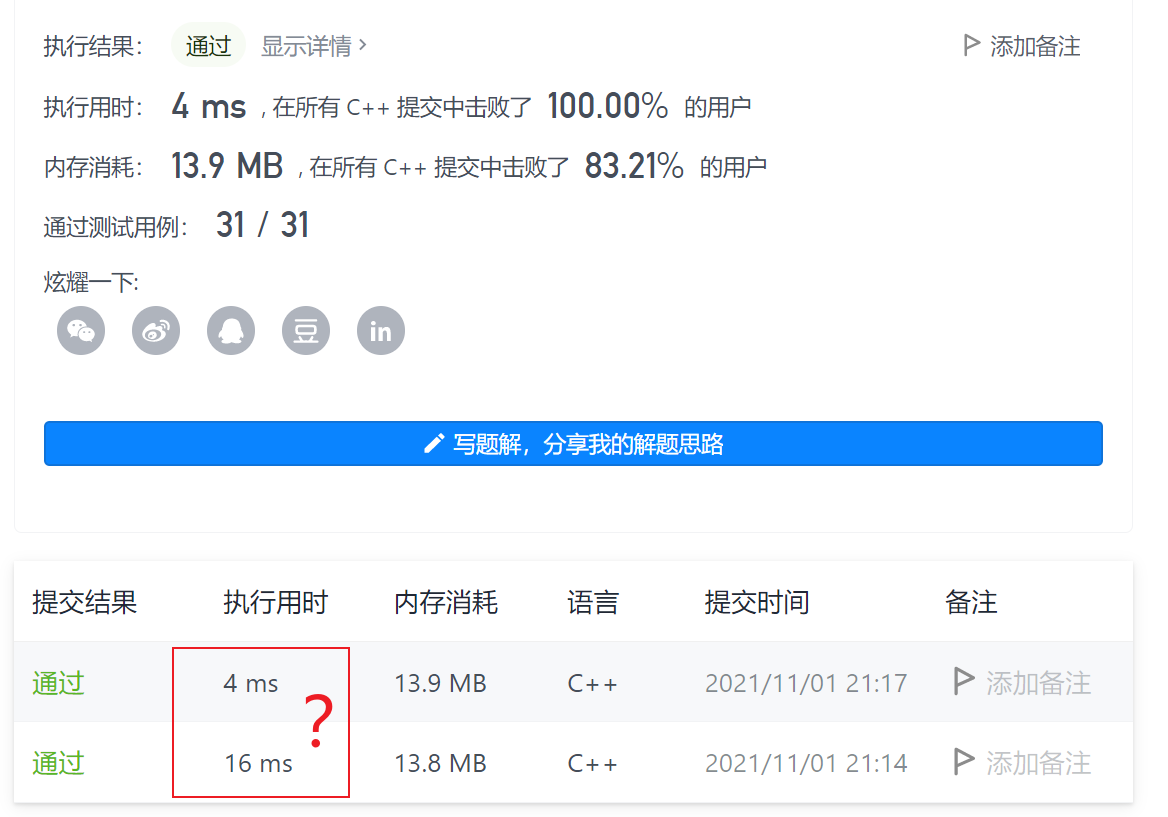
  }
};

精简了一下改了个判断的逻辑为何时间差这么多？
通过此题，对后序遍历和回溯又有了新的认识。

235. 二叉搜索树的最近公共祖先

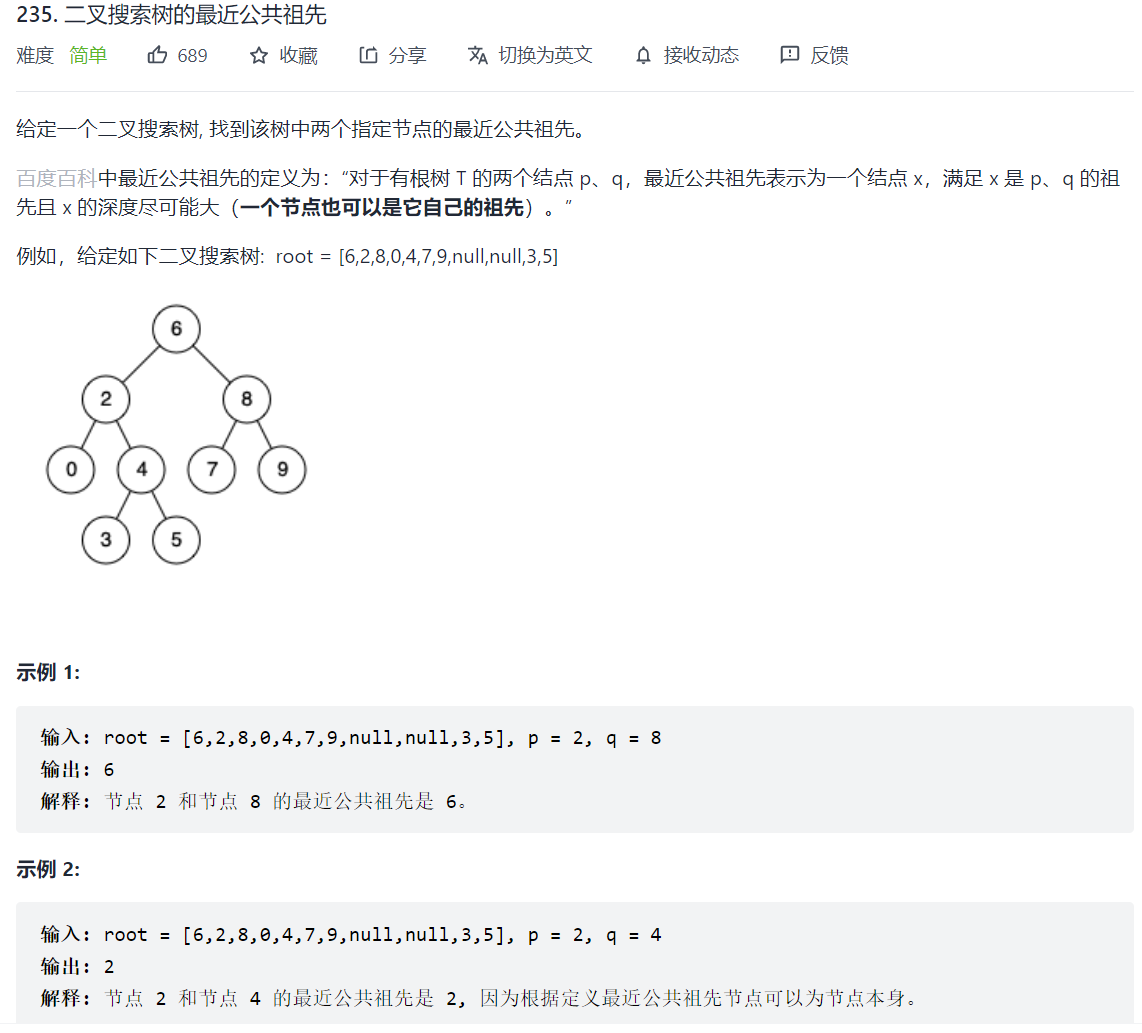
按照一般的二叉树处理

class Solution {
public:
    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
        if (root == p || root == q || !root) return root;

        TreeNode* left = lowestCommonAncestor(root->left, p, q);
        TreeNode* right = lowestCommonAncestor(root->right, p, q);

        if (left && right) return root;
        if (!left) return right;
        return left;
    }
};

利用二叉搜索树的性质

利用二叉树有序的特性，不用回溯，简单的很
搜索树是有序的，每次访问当前节点的时候，假设p->val < q->val,如果当前节点的值在[p->val, q->val]（左闭右闭）之间的话，这个节点一定是公共祖先，因为p一定在左子树上，q一定在右子树上。所以只需判断访问节点是否在区间内即可：

如果在区间内，返回此节点
如果区间在此节点的左边，递归遍历左子树

如果区间在此节点的右边，递归遍历右子树

递归

class Solution {
public:
  TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
      if (!root) return nullptr;

      if (root->val > p->val && root->val > q->val) 
          return lowestCommonAncestor(root->left, p, q);
      else if (root->val < p->val && root->val < q->val)
          return lowestCommonAncestor(root->right, p, q);
      return root;

  }
};

迭代

迭代法就更简单了，直接找就完了

class Solution {
public:
  TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
      while (root) {
          if (root->val > p->val && root->val > q->val) 
              root = root->left;
          else if (root->val < p->val && root->val < q->val)
              root = root->right;
          else break;
      }
      return root;        
  }
};

701. 二叉搜索树中的插入操作

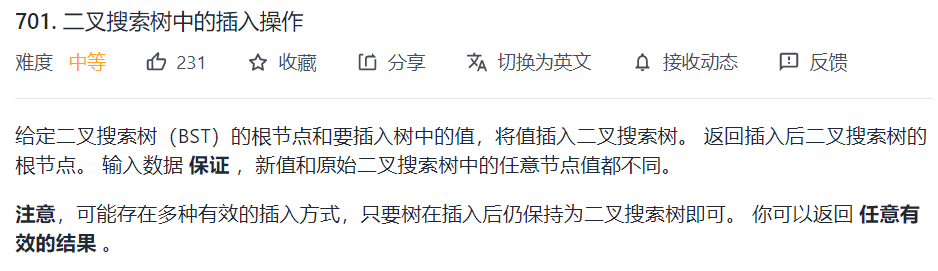
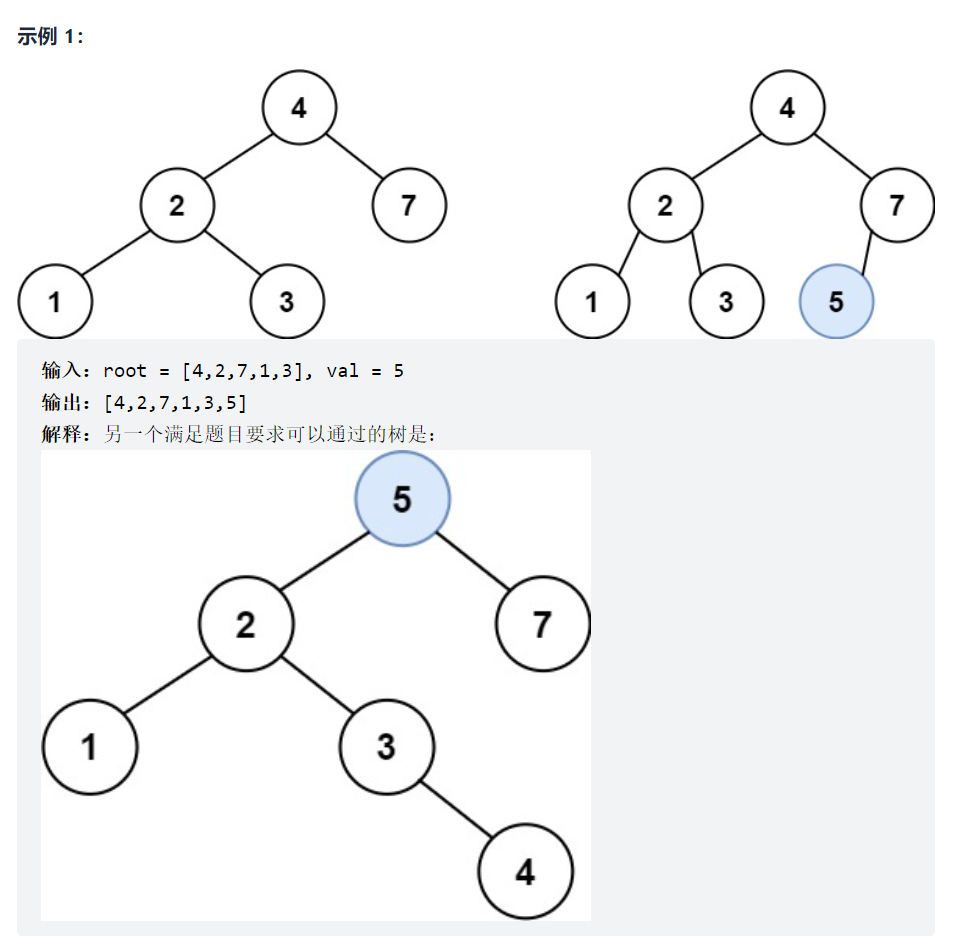
如果不考虑结果的多样性，直接按照方向去遍历，遇到空节点插入就可以了

递归

带返回值的递归函数

使用有返回值的递归函数，可以再遇到空节点后，构造一个新的节点，并让父节点指向它。

递归的参数和返回值

返回值为节点，参数为节点和val

递归的终止条件

如果遇到了空节点，那么就用val构造新的节点并将其返回

if (!root) {
    TreeNode* node = new TreeNode(val);
    return node;
}

单层递归的处理逻辑

如果节点的值大于val，那么搜索左子树
如果节点的值小于val，那么搜索右子树
最后返回根结点

完整代码：

class Solution {
public:
    TreeNode* insertIntoBST(TreeNode* root, int val) {
        if (!root) {
            TreeNode* node = new TreeNode(val);
            return node;
        }

        if (root->val > val) root->left = insertIntoBST(root->left, val);
        if (root->val < val) root->right = insertIntoBST(root->right, val);
        return root;
    }
};

不带返回值的递归函数

递归函数不用返回值也可以，找到插入的节点位置，直接让其父节点指向插入节点，结束递归，也是可以的。

class Solution {
public:
    TreeNode* parent = nullptr;
    void traversal(TreeNode* cur, int val) {
        if (!cur) { // 遇到空节点了
            TreeNode* node = new TreeNode(val);
            if (parent->val > val) parent->left = node;
            else parent->right = node;
            return;
        }
        parent = cur;

        if(cur->val > val) traversal(cur->left, val);
        if(cur->val < val) traversal(cur->right, val);
        return;
    }


    TreeNode* insertIntoBST(TreeNode* root, int val) {
        if (!root) {
            TreeNode* node = new TreeNode(val);
            return node;
        }
        traversal(root, val); // 进入递归是，第一个cur一定不空，parent会被赋值为root
        return root;
    }
};

可以看到有返回值的递归函数还是要方便不少的

迭代

二叉搜索树的迭代就是一个while循环，都一样


class Solution {
public:
    TreeNode* insertIntoBST(TreeNode* root, int val) {
        if (!root) {
            TreeNode* node = new TreeNode(val);
            return node;
        }
        TreeNode* parent = root;
        TreeNode* cur = root;
        while (cur) {
            parent = cur;
            if (cur->val > val) cur = cur->left;
            else cur = cur->right;
        }
        // 找到空节点之后
        TreeNode* node = new TreeNode(val);
        if (parent->val > val) parent->left = node;
        else parent->right = node;

        return root;
    }
};

450. 删除二叉搜索树中的节点

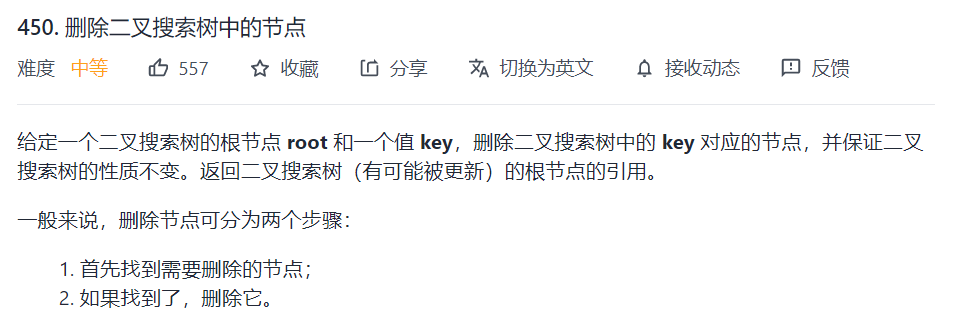
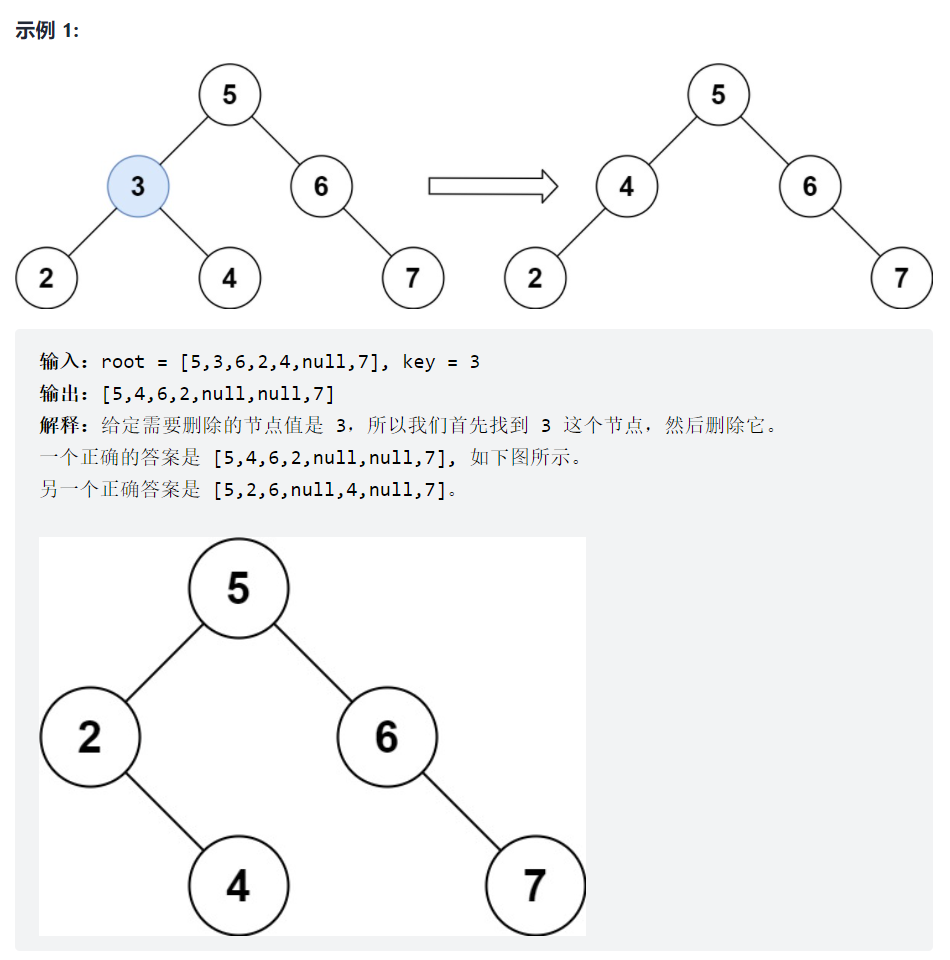
搜索树的节点删除要比增加复杂很多

递归

参数和返回值

类比通过返回值添加节点，通过返回值来删除节点
TreeNode* deleteNode(TreeNode* root, int key)

终止条件

遇到空返回，其实这也说明没找到删除的节点，遍历到空节点直接返回了
if (root == nullptr) return root;

单层递归的逻辑

删除节点遇到的五种情况：

第一种情况：没找到删除的节点，遍历到空节点直接返回了
找到删除的节点
- 第二种情况：左右孩子都为空（叶子节点），直接删除节点，返回NULL为根节点
- 第三种情况：删除节点的左孩子为空，右孩子不为空，删除节点，右孩子补位，返回右孩子为根节点
- 第四种情况：删除节点的右孩子为空，左孩子不为空，删除节点，左孩子补位，返回左孩子为根节点
- 第五种情况：左右孩子节点都不为空，则将删除节点的左子树头结点（左孩子）放到删除节点的右子树的最左面节点的左孩子上，返回删除节点右孩子为新的根节点。（将右子树放到左子树最右端也是可以的）

第五种情况动画：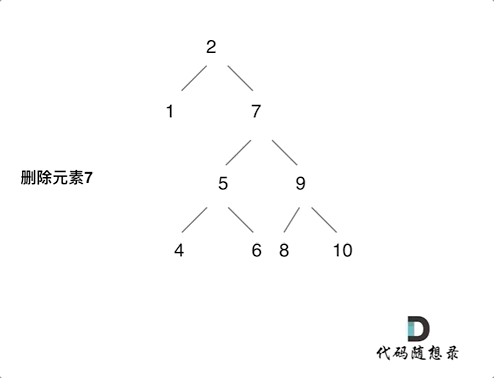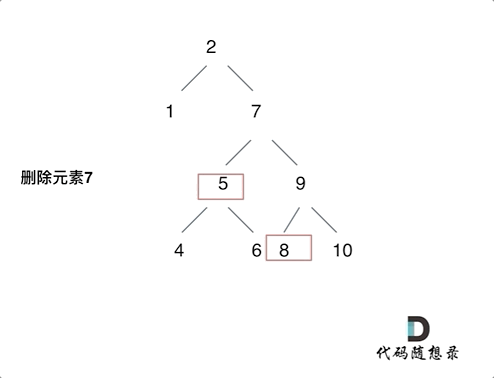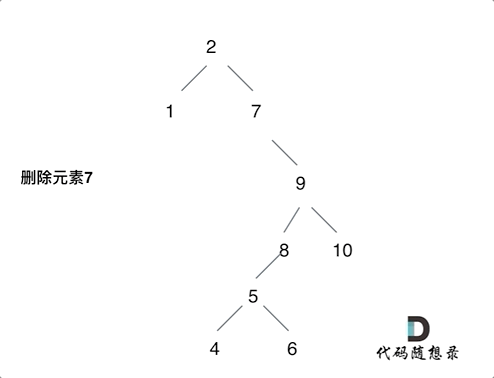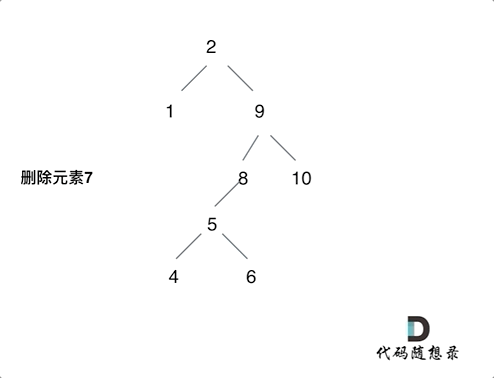

将左子树放到右子树最左端的解法

class Solution {
public:
    TreeNode* deleteNode(TreeNode* root, int key) {
        // 没有找到要删除的节点，遇到空节点直接返回
        if (!root) return root;
        // 找到要删除的节点
        if (root->val == key) {
            // 左右孩子都为空，返回nullptr
            // 左右孩子有一个为空，删除节点，不空的补位
            if (!root->left) return root->right;
            else if (!root->right) return root->left;
            // 左右孩子都不空，将要删除节点的左子树接到右子树最左边的节点上
            else {
                // 寻找右子树最左端的节点
                TreeNode* cur = root->right;
                while(cur->left) {
                    cur = cur->left;
                }
                cur->left = root->left;
                TreeNode* tmp = root;
                root = root->right;
                delete tmp;
                return root;
            }

        }
        if (root->val > key) root->left = deleteNode(root->left, key);
        if (root->val < key) root->right = deleteNode(root->right, key);
        return root;
    }
};

将右子树放到左子树最右端的解法

class Solution {
public:
    TreeNode* deleteNode(TreeNode* root, int key) {
        // 没有找到要删除的节点，遇到空节点直接返回
        if (!root) return root;
        // 找到要删除的节点
        if (root->val == key) {
            // 左右孩子都为空，返回nullptr
            // 左右孩子有一个为空，删除节点，不空的补位
            if (!root->left) return root->right;
            else if (!root->right) return root->left;
            // 左右孩子都不空，将要删除节点的左子树接到右子树最左边的节点上
            else {
                // 寻找右子树最左端的节点
                TreeNode* cur = root->left;
                while(cur->right) {
                    cur = cur->right;
                }
                cur->right = root->right;
                TreeNode* tmp = root;
                root = root->left;
                delete tmp;
                return root;
            }

        }
        if (root->val > key) root->left = deleteNode(root->left, key);
        if (root->val < key) root->right = deleteNode(root->right, key);
        return root;
    }
};

迭代

class Solution {
public:
    TreeNode* deleteOneNode(TreeNode* node) {
        if (!node) return nullptr;
        if (!node->right) return node->left;
        TreeNode* cur = node->right;
        while (cur->left) {
            cur = cur->left;
        }
        cur->left = node->left;
        return node->right;
    }
    TreeNode* deleteNode(TreeNode* root, int key) {
        TreeNode* cur = root;
        TreeNode* pre = nullptr; // cur的父节点，用于删除cur
        while (cur) {
            if (cur->val == key) break;
            pre = cur;
            if (cur->val > key) cur = cur->left;
            else cur = cur->right;
        }
        if (!pre) // 根结点就是要删的值
            return deleteOneNode(cur);

        // pre 要知道是删左孩子还是右孩子
        if (pre->left && pre->left->val == key) {
            pre->left = deleteOneNode(cur);
        }
        if (pre->right && pre->right->val == key) {
            pre->right = deleteOneNode(cur);
        }
        return root;
    }
};

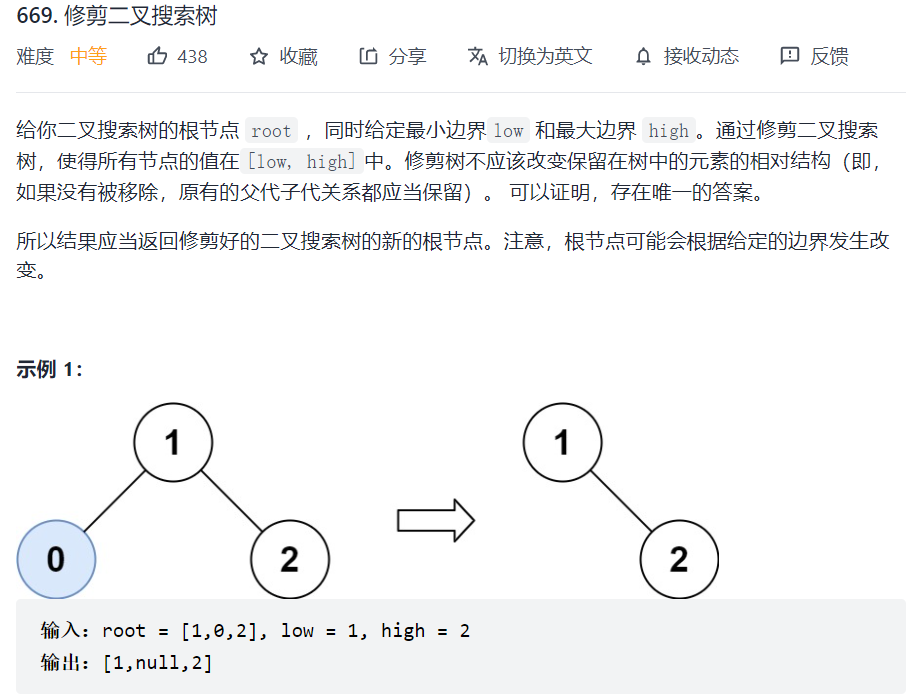
669. 修剪二叉搜索树

递归

这道题不需要重构BST

参数和返回值

需要遍历整棵树，从二叉树中移除节点（用其他节点覆盖），返回值为TreeNode*
参数数节点和区间的上下限

终止条件

当遇到空节点时，返回nullptr

单层递归的逻辑

如果当前节点在区间内，那么去左右子树查找不符合条件的节点
如果节点的值比high要大，那么要将左子树处理的结果赋值给这个节点
如果节点的值比low要小，那么要将右子树处理的结果赋值给这个节点

if (root->val < low) {
    return trimBST(root->right, low, high); // 符合条件的节点一定在右子树
}
if (root->val > high) {
    return trimBST(root->left, low, high);  // 符合条件的节点一定在左子树
}
// 节点在区间内，处理左右子树
root->left = trimBST(root->left, low, high); // root->left接入符合条件的左孩子
root->right = trimBST(root->right, low, high); // root->right接入符合条件的右孩子
return root;

完整代码：

class Solution {
public:
    TreeNode* trimBST(TreeNode* root, int low, int high) {
        if (!root) return nullptr;
        if (root->val < low) return trimBST(root->right, low, high); 
        if (root->val > high) return trimBST(root->left, low, high);
        root->left = trimBST(root->left, low, high); // root->left接入符合条件的左孩子
        root->right = trimBST(root->right, low, high); // root->right接入符合条件的右孩子
        return root;
    }
};

迭代法

class Solution {
public:
    TreeNode* trimBST(TreeNode* root, int L, int R) {
        if (!root) return nullptr;

        // 处理头结点，让root移动到[L, R] 范围内，注意是左闭右闭
        while (root != nullptr && (root->val < L || root->val > R)) {
            if (root->val < L) root = root->right; // 小于L往右走
            else root = root->left; // 大于R往左走
        }
        TreeNode *cur = root;
        // 此时root已经在[L, R] 范围内，处理左孩子元素小于L的情况
        while (cur != nullptr) {
            while (cur->left && cur->left->val < L) {
                cur->left = cur->left->right;
            }
            cur = cur->left;
        }
        cur = root;

        // 此时root已经在[L, R] 范围内，处理右孩子大于R的情况
        while (cur != nullptr) {
            while (cur->right && cur->right->val > R) {
                cur->right = cur->right->left;
            }
            cur = cur->right;
        }
        return root;
    }
};

108. 将有序数组转换为二叉搜索树

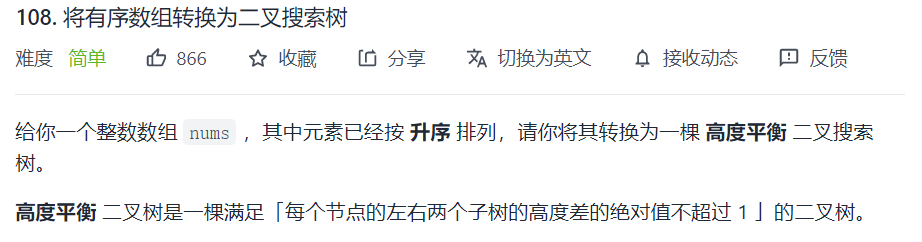
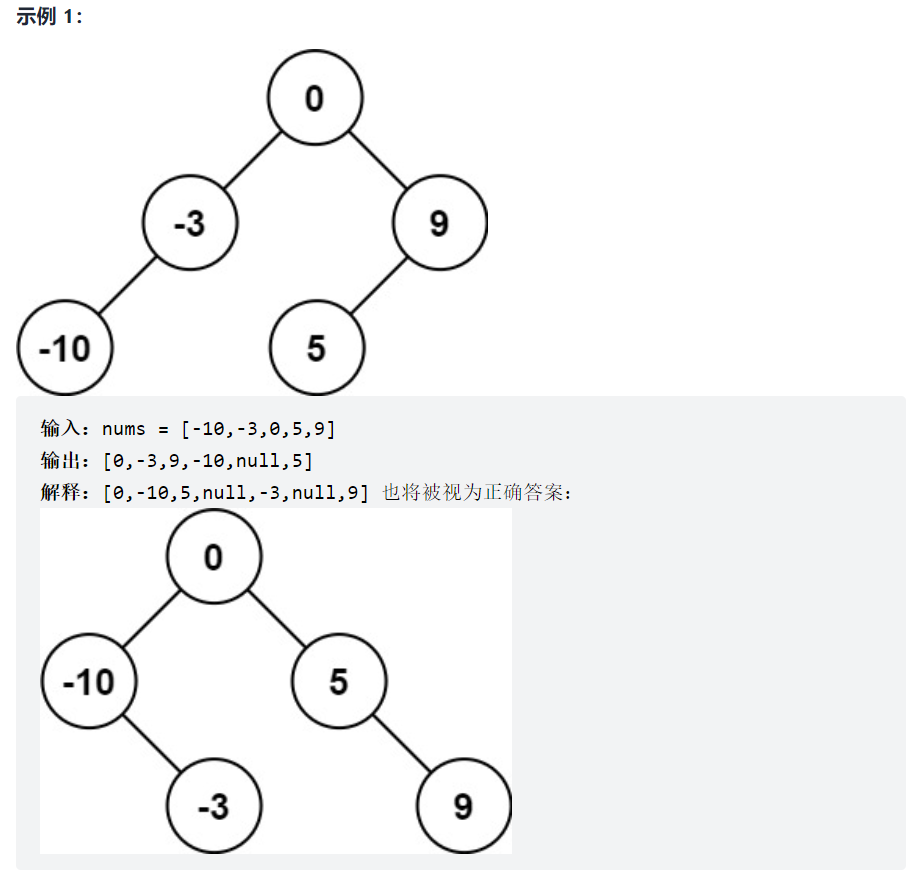
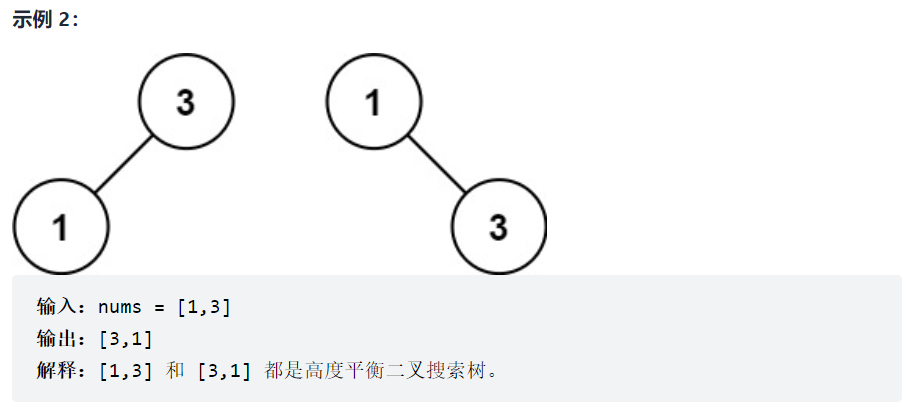
数组本身有序，从数组的中间节点（如果数组长度为偶数，取左边的，取右边也可，这是结果不唯一的原因）开始构造二叉搜索树，构造出来的本身就是平衡的。不要从头添加再去调平衡，那样很麻烦

递归

参数和返回值

返回节点的指针，用于构造树，参数为有序数组和处理的范围
TreeNode* buildBST(vector<int>& nums, int left, int high)

终止条件

左闭右闭，left > right时是空节点
if(left > right) return nullptr;

单层递归的逻辑

为了避免越界，查找mid这么写：int mid = left + ((right - left) >> 1);
注：int mid = (left + right) / 2;，这么写的话，left和right中有一个是最大整数就越界了

用mid来构造节点

TreeNode* root = new TreeNode(nums[mid]);
root->left = traversal(nums, left, mid - 1);
root->right = traversal(nums, mid + 1, right);
return root;

完整代码：

class Solution {
public:
    TreeNode* buildBST(vector<int>& nums, int left, int right) {
        if (left > right) return nullptr;
        int mid = left + ((right - left) >> 1);
        TreeNode* root = new TreeNode(nums[mid]);
        root->left = buildBST(nums, left, mid - 1);
        root->right = buildBST(nums, mid + 1, right);
        return root;
    }
    TreeNode* sortedArrayToBST(vector<int>& nums) {
         return buildBST(nums, 0, nums.size() - 1);
    }
};

迭代

class Solution {
public:
    TreeNode* sortedArrayToBST(vector<int>& nums) {
        if (nums.size() == 0) return nullptr;

        TreeNode* root = new TreeNode(0);   // 初始根节点
        queue<TreeNode*> nodeQue;           // 放遍历的节点
        queue<int> leftQue;                 // 保存左区间下表
        queue<int> rightQue;                // 保存右区间下表
        nodeQue.push(root);                 // 根节点入队列
        leftQue.push(0);                    // 0为左区间下表初始位置
        rightQue.push(nums.size() - 1);     // nums.size() - 1为右区间下表初始位置

        while (!nodeQue.empty()) {
            TreeNode* curNode = nodeQue.front();
            nodeQue.pop();
            int left = leftQue.front(); leftQue.pop();
            int right = rightQue.front(); rightQue.pop();
            int mid = left + ((right - left) / 2);

            curNode->val = nums[mid];       // 将mid对应的元素给中间节点

            if (left <= mid - 1) {          // 处理左区间
                curNode->left = new TreeNode(0);
                nodeQue.push(curNode->left);
                leftQue.push(left);
                rightQue.push(mid - 1);
            }

            if (right >= mid + 1) {         // 处理右区间
                curNode->right = new TreeNode(0);
                nodeQue.push(curNode->right);
                leftQue.push(mid + 1);
                rightQue.push(right);
            }
        }
        return root;
    }
};

1382. 将二叉搜索树变平衡

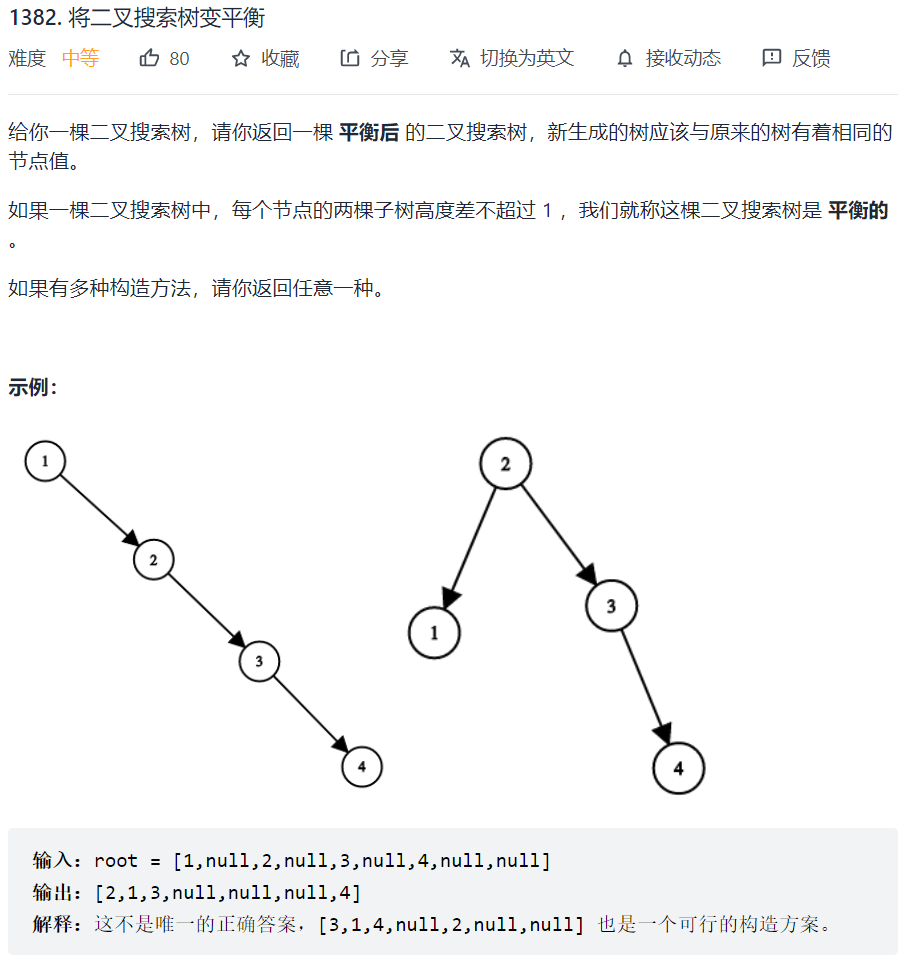
先中序遍历得到有序数组，然后就变成了用有序数组构造二叉搜索树，和108. 将有序数组转换为二叉搜索树一样了

class Solution {
public:
    void traversal(TreeNode* root, vector<int>& nums) {
        if (!root) return;
        traversal(root->left, nums);
        nums.push_back(root->val);
        traversal(root->right, nums);
    }
    TreeNode* build(vector<int>& nums, int left, int right) {
        if (left > right) return nullptr;
        int mid = left + ((right - left) >> 1);
        TreeNode* root = new TreeNode(nums[mid]);
        root->left = build(nums, left, mid - 1);
        root->right = build(nums, mid + 1, right);
        return root;
    }
    TreeNode* balanceBST(TreeNode* root) {
        vector<int> nums;
        traversal(root, nums);
        return build(nums, 0, nums.size() - 1);
    }
};

538. 把二叉搜索树转换为累加树

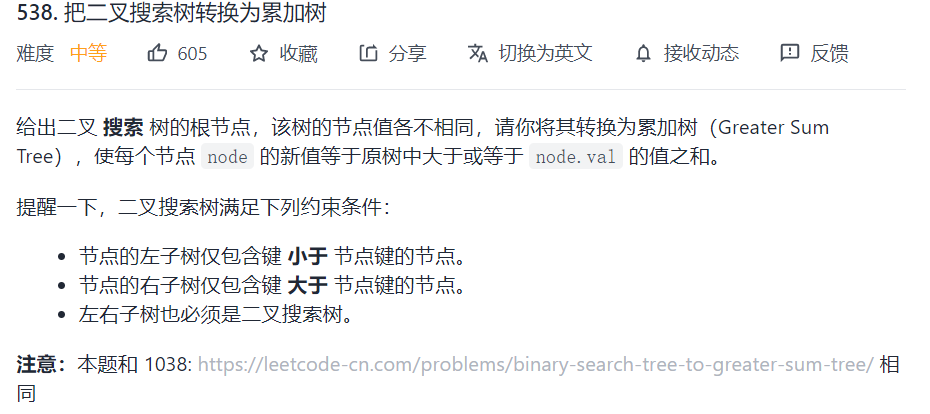
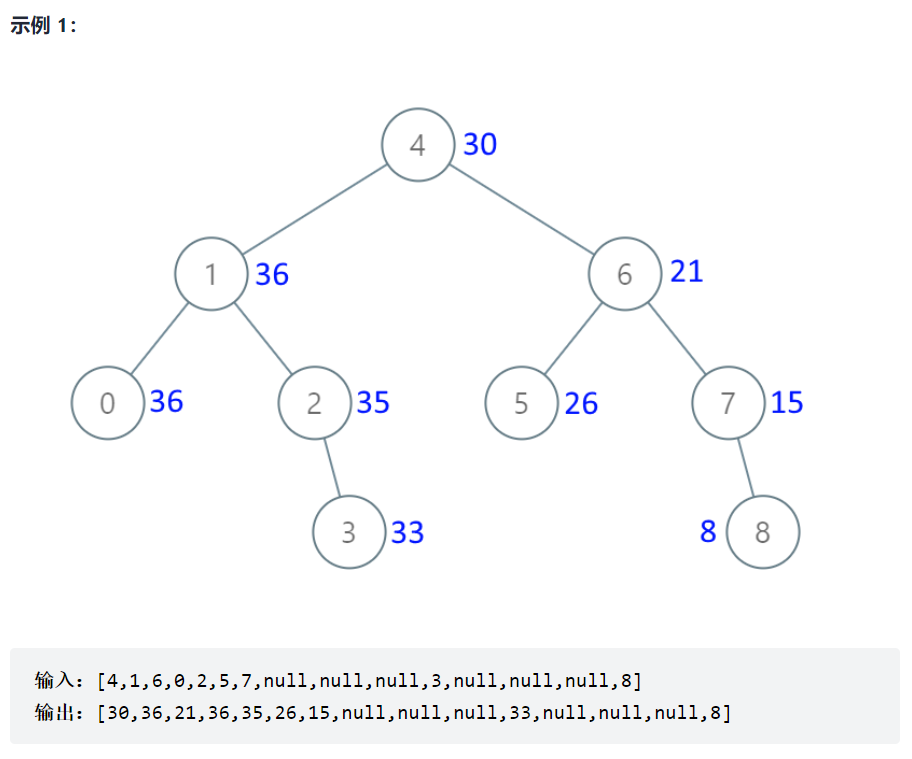
这道题就是右中左的遍历顺序，并用一个值来记录已经访问过的节点和（这个节点和就是上一个访问的节点的值），或者用一个指针记录上一次访问的节点，每当访问一个新的节点时，将值加到上面就可以了

递归

递归函数无返回值

class Solution {
public:
    void traversal(TreeNode* cur, int& sum) {
        if (!cur) return;
        traversal(cur->right, sum); // 右
        // 中
        int tmp = cur->val;
        cur->val += sum;
        sum += tmp;
        traversal(cur->left, sum); // 左
    }
    TreeNode* convertBST(TreeNode* root) {
        int sum = 0;
        traversal(root, sum);
        return root;
    }
};

递归函数有返回值

class Solution {
public:
    int sum = 0;
    TreeNode* convertBST(TreeNode* root) {
        if (!root) return nullptr;
        root->right = convertBST(root->right);
        int tmp = root->val;
        root->val += sum;
        sum += tmp;
        root->left = convertBST(root->left);
        return root;
    }
};

用pre记录前一个节点的版本

class Solution {
public:
    TreeNode* pre = nullptr;
    TreeNode* convertBST(TreeNode* root) {
        if (!root) return nullptr;
        root->right = convertBST(root->right); // 右
        // 中
        if (pre)
            root->val += pre->val;
        pre = root;

        root->left = convertBST(root->left); // 左
        return root;
    }
};

迭代法

写一个右中左的反向中序遍历

class Solution {
public:

    TreeNode* convertBST(TreeNode* root) {
        if (!root) return nullptr;
        int pre = 0;
        TreeNode* cur = root;
        stack<TreeNode*> st;
        while (cur || !st.empty()) {
            if (cur) {
                st.push(cur);
                cur = cur->right; // 右
            } else {
                // 中
                cur = st.top(); st.pop();
                cur->val += pre;
                pre = cur->val;

                cur = cur->left; // 左
            }
        }
        return root;
    }
};

迭代法还挺快。

二叉搜索树

递归法

迭代法

总结

陷阱

思路一

思路二

思路三 迭代

思路一：将树转换为数组

思路二：在遍历树的过程中记录差值

思路三：用栈来模拟中序遍历

思路一：当成普通二叉树来处理

思路二：

转化为数组处理

直接在中序遍历中进行统计

用栈来模拟中序遍历的迭代法

思路：用后序遍历遍历整根树

按照一般的二叉树处理

利用二叉搜索树的性质

递归

迭代

递归

带返回值的递归函数

不带返回值的递归函数

迭代

递归

迭代

递归

迭代法

递归

迭代

递归

迭代法

思路三迭代