1091. 二进制矩阵中的最短路径

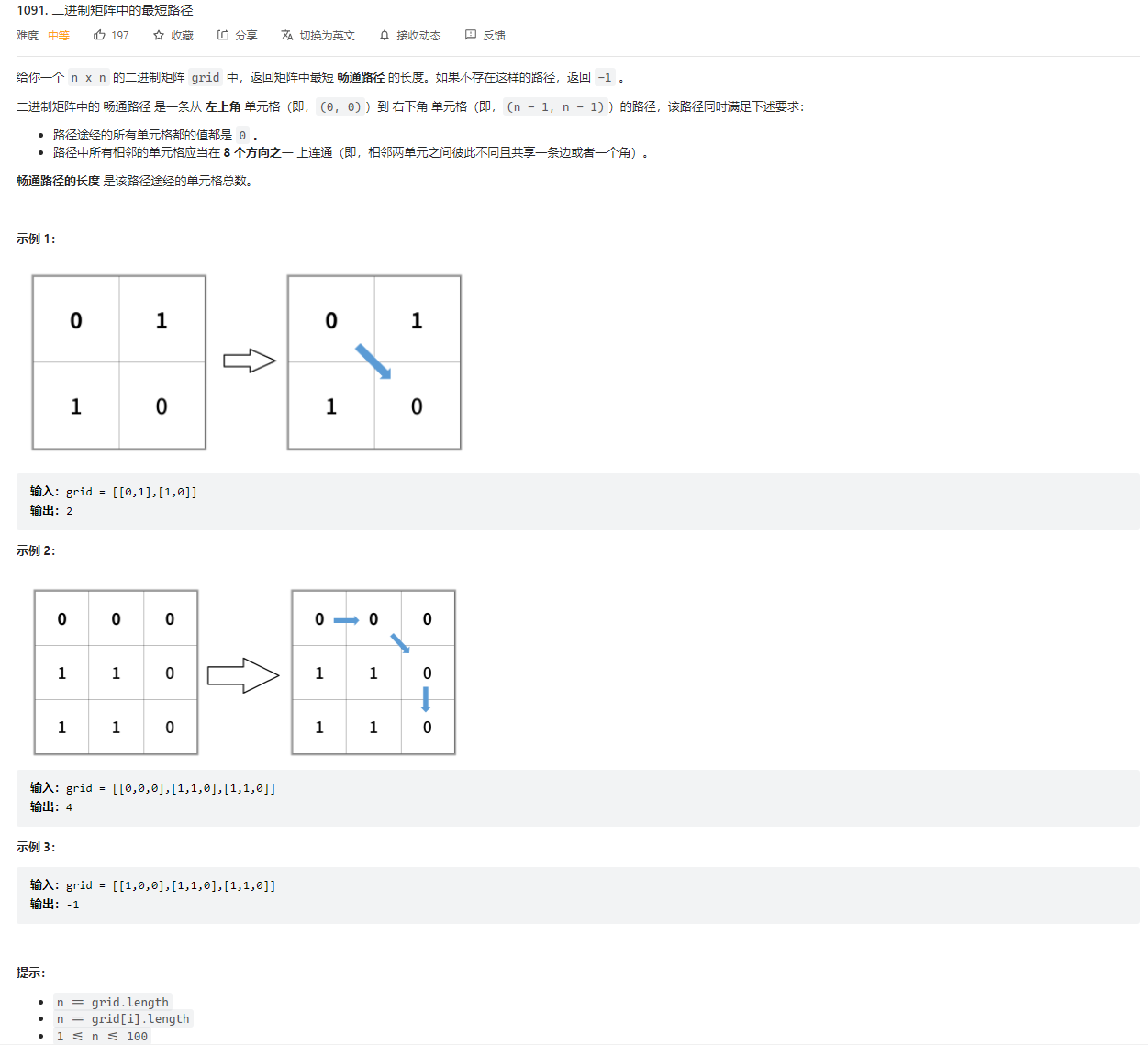
class Solution {
public:
    typedef pair<int, int> PII;
    int shortestPathBinaryMatrix(vector<vector<int>>& grid) {
        if (grid[0][0] == 1) return -1;
        int dx[8] = {1, 0, -1, 0, 1, 1, -1, -1}, dy[8] = {0, 1, 0, -1, 1, -1, -1, 1};
        int n = grid.size();
        vector<vector<int>> d(n, vector<int>(n, -1));
        queue<PII> q;
        q.push({0, 0});
        d[0][0] = 1;
        while (!q.empty()) {
            auto t = q.front();
            q.pop();
            for (int i = 0; i < 8; i++) {
                int x = t.first + dx[i], y = t.second + dy[i];
                if (x >= 0 && x < n && y >= 0 && y < n && grid[x][y] == 0 && d[x][y] == -1) {
                    d[x][y] = d[t.first][t.second] + 1;
                    q.push({x, y});
                }
            }
        }
        return d[n - 1][n - 1];
    }
};

773. 滑动谜题

class Solution {
public:
    int dx[4] = {1, 0, -1, 0}, dy[4] = {0, 1, 0, -1};
    int bfs(string state) {
        queue<string> q;
        unordered_map<string, int> d;
        string end = "123450";

        q.push(state);
        d[state] = 0;

        while (!q.empty()) {
            auto t =  q.front();
            q.pop();
            if (t == end) return d[t];

            int distance = d[t];
            int k = t.find('0');
            int x = k / 3, y = k % 3;
            for (int i = 0; i < 4; i++) {
                int a = x + dx[i], b = y + dy[i];
                if (a >= 0 && a < 2 && b >= 0 && b < 3) {
                    swap(t[k], t[a * 3 + b]);
                    if (!d.count(t)) {
                        d[t] = distance + 1;
                        q.push(t);
                    }
                    swap(t[k], t[a * 3 + b]);
                }
            }
        }
        return -1;
    }
    int slidingPuzzle(vector<vector<int>>& board) {
        string start;
        for (const auto& v : board) {
            for (const auto& n : v) {
                start.push_back(n + '0');
            }
        }
        return bfs(start);
    }
};

面试题 08.02. 迷路的机器人

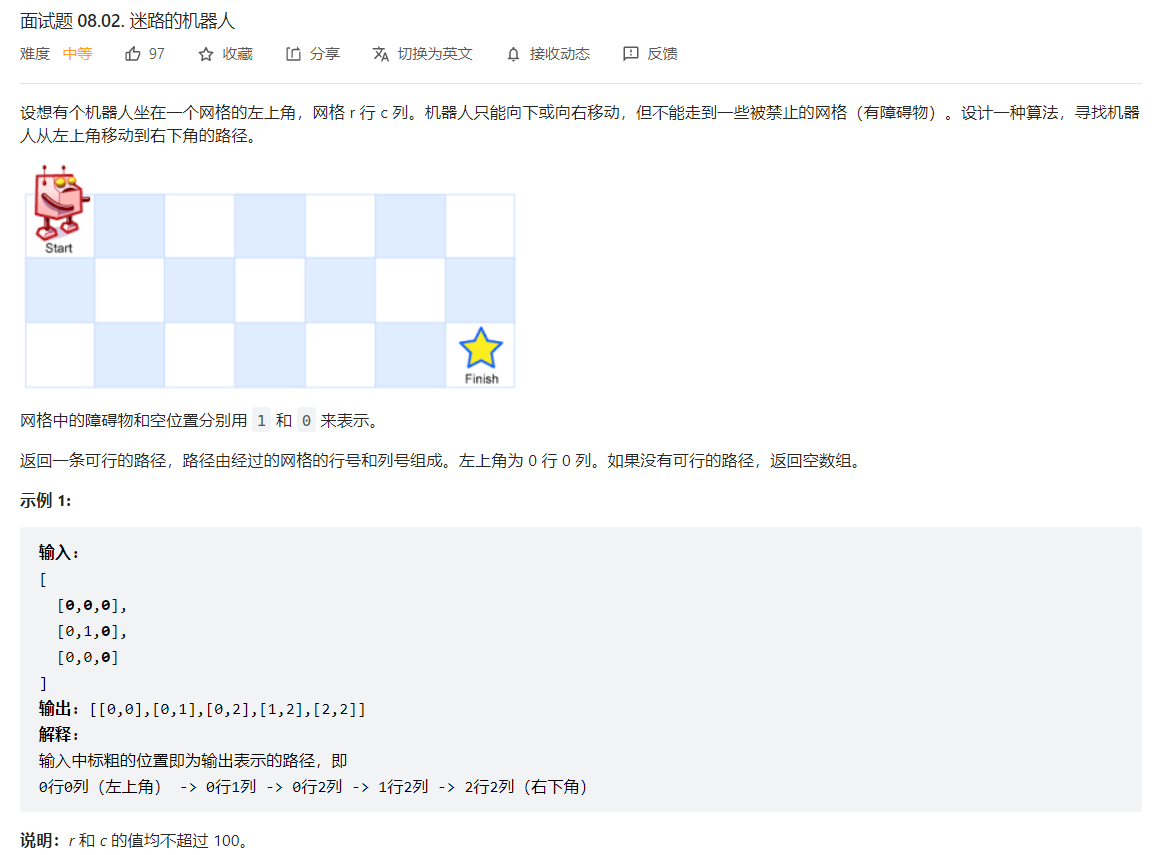
dp记录转移位置

class Solution {
public:
    vector<vector<int>> pathWithObstacles(vector<vector<int>>& obstacleGrid) {
        int m = obstacleGrid.size(), n = obstacleGrid[0].size();
        vector<vector<int>> res;
        if (obstacleGrid[0][0] == 1 || obstacleGrid[m - 1][n - 1] == 1) return res;

        vector<vector<int>> path(m, vector<int>(n, -1));
        path[0][0] = 0;

        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++) {
                if ((i == 0 && j == 0) || obstacleGrid[i][j] == 1) continue;
                if (i > 0 && path[i - 1][j] >= 0)
                    path[i][j] = (i - 1) * n + j;
                if (j > 0 && path[i][j - 1] >= 0)
                    path[i][j] = i * n + j - 1;
            }
        }

        int i = m - 1, j = n - 1;
        if (path[i][j] == -1) return {};

        while (i != 0 || j != 0) {
            res.push_back({i, j});
            int t = path[i][j];
            i = t / n;
            j = t % n;
        }
        res.push_back({i, j}); // 插入起点
        reverse(res.begin(), res.end());
        return res;
    }
};

BFS记录转移位置

class Solution {
public:
    vector<vector<int>> pathWithObstacles(vector<vector<int>>& obstacleGrid) {
        int m = obstacleGrid.size(), n = obstacleGrid[0].size();
        vector<vector<int>> res;
        if (obstacleGrid[0][0] == 1 || obstacleGrid[m - 1][n - 1] == 1) return {};
        vector<vector<int>> path(m, vector<int>(n, -1));
        path[0][0] = 0;
        int dx[2] = {1, 0}, dy[2] = {0, 1};

        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++) {
                if (obstacleGrid[i][j] == 1 || path[i][j] == -1) continue;
                for (int k = 0; k < 2; k++) {
                    int x = i + dx[k], y = j + dy[k];
                    if (x < m && y < n && obstacleGrid[x][y] != 1 && path[x][y] == -1) {
                        path[x][y] = i * n + j; // 记录来的位置
                    }
                }
            }
        }

        int i = m - 1, j = n - 1;
        if (path[i][j] == -1) return {};

        res.push_back({i, j});
        while (i > 0 || j > 0) {
            int t = path[i][j];
            i = t / n;
            j = t % n;
            res.push_back({i, j});
        }
        reverse(res.begin(), res.end());
        return res;
    }
};