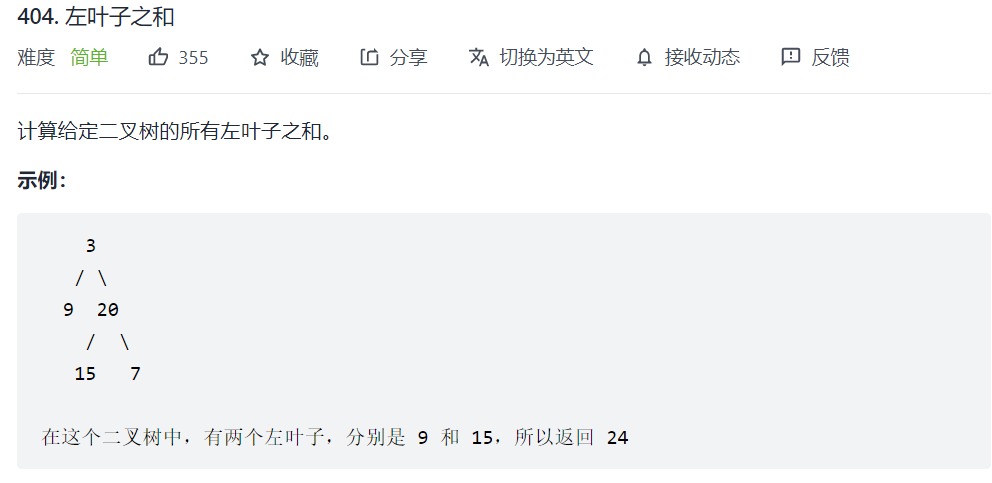
404. 左叶子之和
递归法
class Solution {
public:
int sumOfLeftLeaves(TreeNode* root) {
if (!root) return 0;
int sum = 0;
if (root->left && !root->left->left && !root->left->right) // root->left是左叶子
sum = root->left->val;
return sum + sumOfLeftLeaves(root->left) + sumOfLeftLeaves(root->right);
}
};
迭代法
迭代法处理左叶子节点的逻辑和递归法是一样的,只不过要用栈来模拟递归的过程
class Solution {
public:
int sumOfLeftLeaves(TreeNode* root) {
if (!root) return 0;
int sum = 0;
stack<TreeNode*> stk;
stk.push(root);
while (!stk.empty()) {
TreeNode* cur = stk.top();
stk.pop();
if (cur->left && !cur->left->left && !cur->left->right)
sum += cur->left->val;
if (cur->right) stk.push(cur->right);
if (cur->left) stk.push(cur->left);
}
return sum;
}
};
 速度还挺快的!!
速度还挺快的!!
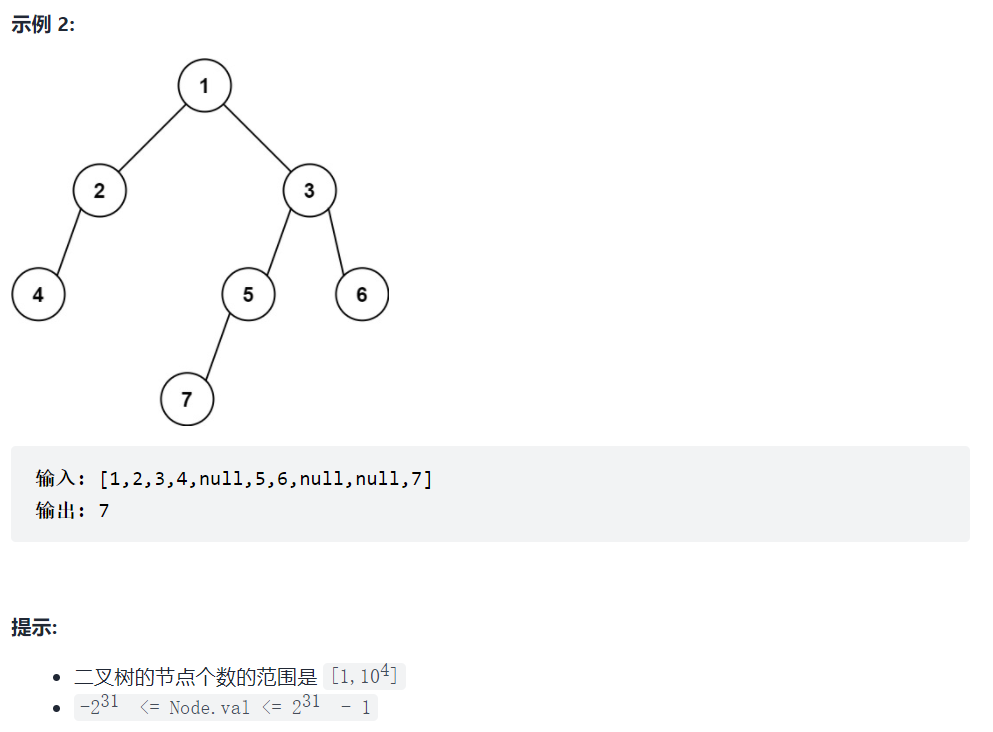
513. 找树左下角的值
迭代法
捕捉关键字,最底层、最左边
看到最底层,立马想到用层序遍历可能会比较简单
那么可以利用层序遍历的模板,稍微修改一下,用一个变量记录每一层的最左边的节点,那么层序遍历结束后,这个变量的值就是最底层 最左边的节点的值了
class Solution {
public:
int findBottomLeftValue(TreeNode* root) {
// 二叉树至少有一个节点,因此不写判空条件
queue<TreeNode*> que;
que.push(root);
int res;
while (!que.empty()) {
int size = que.size();
//记录每一层最左节点的值
res = que.front()->val;
for (int i = 0; i < size; i++) {
TreeNode* cur = que.front();
que.pop();
if (cur->left) que.push(cur->left);
if (cur->right) que.push(cur->right);
}
}
return res;
}
};
递归法
相较于迭代法,递归法就要麻烦许多了
首先要判断最底层,这时候要用到求节点的深度,然后用前序遍历优先搜索左面,记录深度最大的叶子结点,此式就是树的最后一行最左边的值
- 确定递归函数的参数和返回值
参数必须有要遍历的树的根节点,还有就是一个int型的变量用来记录最长深度。 这里就不需要返回值了,所以递归函数的返回类型为void。
本题还需要类里的两个全局变量,maxLen用来记录最大深度,maxleftValue记录最大深度最左节点的数值。
int maxLen = INT_MIN; // 全局变量 记录最大深度
int maxleftValue; // 全局变量 最大深度最左节点的数值
void traversal(TreeNode* root, int leftLen)
- 确定终止条件
当遇到叶子节点的时候,就需要统计一下最大的深度了,所以需要遇到叶子节点来更新最大深度。
if (root->left == NULL && root->right == NULL) {
if (leftLen > maxLen) {
maxLen = leftLen; // 更新最大深度
maxleftValue = root->val; // 最大深度最左面的数值
}
return;
}
- 确定单层递归的逻辑
在找最大深度的时候,递归的过程中依然要使用回溯,代码如下:
if (root->left) { // 左
leftLen++; // 深度加一
traversal(root->left, leftLen);
leftLen--; // 回溯,深度减一
}
if (root->right) { // 右
leftLen++; // 深度加一
traversal(root->right, leftLen);
leftLen--; // 回溯,深度减一
}
return;
完整代码:
class Solution {
public:
int maxLen = INT_MIN;
int maxleftValue;
void traversal(TreeNode* root, int leftLen) {
if (root->left == NULL && root->right == NULL) {
if (leftLen > maxLen) {
maxLen = leftLen;
maxleftValue = root->val;
}
return;
}
if (root->left) {
leftLen++;
traversal(root->left, leftLen);
leftLen--; // 回溯
}
if (root->right) {
leftLen++;
traversal(root->right, leftLen);
leftLen--; // 回溯
}
return;
}
int findBottomLeftValue(TreeNode* root) {
traversal(root, 0);
return maxleftValue;
}
};
精简一下:
class Solution {
public:
int maxLen = INT_MIN;
int maxleftValue;
void traversal(TreeNode* root, int leftLen) {
// 先序遍历一定先访问左节点,如果左节点是叶子节点,那么处理
if (root->left == NULL && root->right == NULL) {
if (leftLen > maxLen) {
maxLen = leftLen;
maxleftValue = root->val;
}
return;
}
if (root->left) {
traversal(root->left, leftLen + 1); // 隐藏着回溯
}
if (root->right) {
traversal(root->right, leftLen + 1); // 隐藏着回溯
}
return;
}
int findBottomLeftValue(TreeNode* root) {
traversal(root, 0);
return maxleftValue;
}
};