什么是动态规划
动态规划,英文:Dynamic Programming,简称DP,如果某一问题有很多重叠子问题,使用动态规划是最有效的。
所以动态规划中每一个状态一定是由上一个状态推导出来的,这一点就区分于贪心,贪心没有状态推导,而是从局部直接选最优的
动态规划和贪心的区别:动规是由前一个状态推导出来的,而贪心是局部直接选最优的。
两个角度思考:
- 状态表示:
- dp数组的含义
- max,min …
- 状态计算
- 集合的划分
背包问题
背包九讲—对于找工作面试来说,掌握01背包和完全背包就可以了
背包问题九讲 2.0.pdf
背包问题是一种组合优化的 NP 完全问题:有 N 个物品和容量为 W 的背包,每个物品都有
自己的体积 w 和价值 v,求拿哪些物品可以使得背包所装下物品的总价值最大。大概分为两种:
- 0-1 背包问题:限定每种物品只能选择 0 个或 1 个
- 无界背包问题或完全背包问题:不限定每种物品的数量,一个物品可以拿多次
0-1背包
有N件物品和一个最多能背重量为W 的背包。第i件物品的重量是weight[i],得到的价值是value[i] 。每件物品只能用一次,求解将哪些物品装入背包里物品价值总和最大。
每件物品都有选与不选两种情况,那么这个问题完全可以用回溯法来暴力搜索,时间复杂度为,因为暴力解法时间复杂度太高,所以才要用动态规划优化
二维dp
定义二维dp数组,dp[i][j] 表示前i件物品在体积不超过j的情况下的最大价值
- 不选第i件物品:dp[i][j] = dp[i-1][j]
- 选第i件物品:dp[i][j] = dp[i - 1][j - w] + v
前 i 件物品的最大价值取决于前 i-1 件物品的最大价值,如果第 i 件商品放入背包,假设其价值为v,重量为w,那么应该,前 i-1 件商品重量不能超过 j-w,其中dp[i-1][j-w] 表示背包容量为 j-w 时不放物品i的最大值
那么可以得到状态转移方程:
j的范围为1 ~ N,也就是假设一共N个背包,每个背包都要求最优解,假如说我要把这件物品放入背包j,就必须满足在背包最大容量为 j - w的情况下,加上这件物品的价值后,背包里物品的总价值比我不把这件商品放进去要大才行。
总时间复杂度和空间复杂度都为 O(NW)。
int knapsack(vector<int> weights, vector<int> values, int N, int W) {// weights : 每件商品的重量// values: 每件商品的价值// N : 商品的件数// W : 背包的容量vector<vector<int>> dp(N + 1, vector<int>(W + 1, 0));for (int i = 1; i <= N; ++i) {int w = weights[i - 1], v = values[i - 1]; // 取当前物品的重量和价值for (int j = 1; j <= W; ++j) { // 处理背包容量不同的情况if (j >= w) {//背包还能装下//取装和不装的最大值dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - w] + v);} else { // 背包装不下了dp[i][j] = dp[i - 1][j];}}}return dp[N][W];}
例子: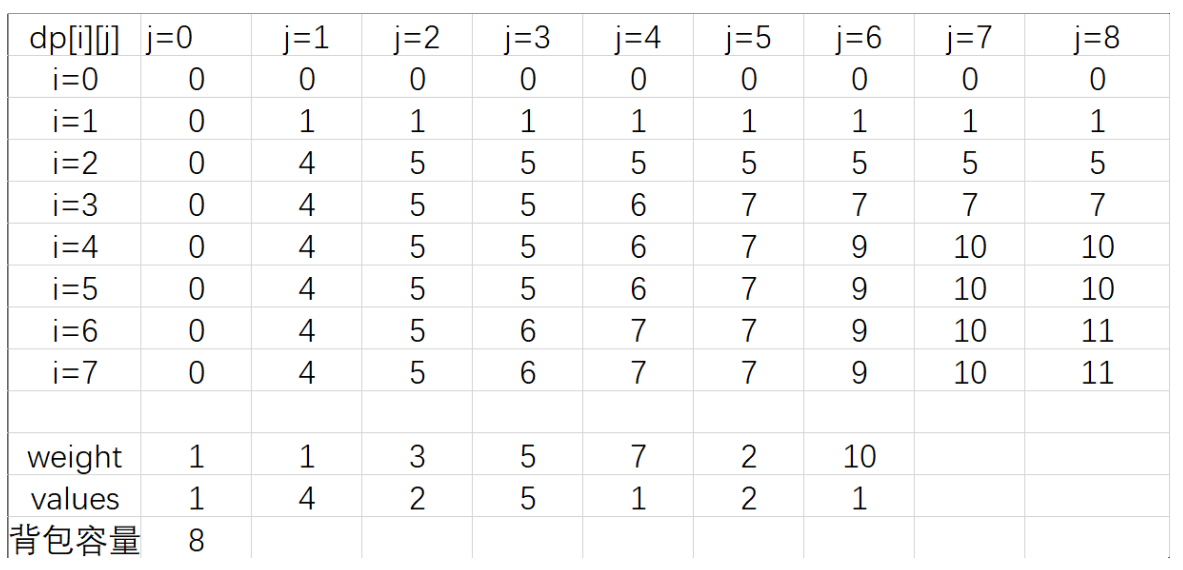
优化空间复杂度
我们可以进一步对 0-1 背包进行空间优化(滚动数组),将空间复杂度降低为 O(W)。如图所示,假设我们目前考虑物品
i = 2,且其体积为 w = 2,价值为 v = 3;对于背包容量 j,我们可以得到
这里可以发现我们永远只依赖于上一排 i = 1 的信息,之前算过的其他物品都不需要再使用。因此我们可以去掉 dp 矩阵的第一个维度,在考虑物品 i 时变成。这里要注意我们在遍历每一行的时候必须逆向遍历,这样才能够调用上一行物品 i-1 时 dp[j-w] 的值;若按照从左往右的顺序进行正向遍历,则 dp[j-w] 的值在遍历到 j 之前就已经被更新成物品 i 的值了。
int knapsack(vector<int> weights, vector<int> values, int N, int W) {
// weights : 每件商品的重量
// values: 每件商品的价值
// N : 商品的件数
// W : 背包的容量
vector<int> dp(W + 1, 0);
for (int i = 1; i <= N; ++i) {
int w = weights[i - 1], v = values[i - 1];
for (int j = W; j >= w; --j) {
dp[i][j] = max(dp[j], dp[j - w] + v);
}
}
return dp[W];
}
背包恰好装满的情况
上面讨论的都是不考虑背包是否装满的情况,假如要求背包恰好装满时,最大的价值是多少,就需要将dp[0],置为0,其他元素全部置为负无穷,如果dp[i]的值不是从dp[0]转移而来,那么dp[j]的值会是负数,最后迭代完成后,如果dp[W]是正数,则说明存在最大值,反之不存在。
代码:
int knapsack(vector<int> weights, vector<int> values, int N, int W) {
// weights : 每件商品的重量
// values: 每件商品的价值
// N : 商品的件数
// W : 背包的容量
vector<int> dp(W + 1, INT32_MIN);
dp[0] = 0;
for (int i = 1; i <= N; ++i) {
int w = weights[i - 1], v = values[i - 1];
for (int j = W; j >= w; --j) {
dp[i][j] = max(dp[j], dp[j - w] + v);
}
}
if (dp[W] < 0)
dp[W] = 0; // 无解记为0
return dp[W];
}
完全背包问题
01背包每件物品只可以选择一次,完全背包问题每件物品可以选择无限次
首先根据01背包问题的思路思考完全背包问题
记dp[i][j]为背包容量为j时,在前i件物品中取一定数量的物品,每件物品可以拿多次,得到的最大价值
假设每件物品拿的次数为k,那么在遍历时可以加一层循环,来遍历k取不同值时背包的价值,取最大值即可
dp[i - 1][j - k v[i]] + k w[i]表示第i件物品取k件的价值
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 1010;
int m, n; // m 是物品件数 n是背包容积
int v[N], w[N], dp[N][N];
int main() {
cin >> m >> n;
for (int i = 1; i <= m; ++i) cin >> v[i] >> w[i];
for (int i = 1; i <= m; ++i)
for (int j = 0; j <= n; ++j)
for (int k = 0; k * v[i] <= j; ++k)
dp[i][j] = max(dp[i][j], dp[i - 1][j - k * v[i]] + k * w[i]);
cout << dp[m][n] << endl;
return 0;
这样写时间复杂度很高,第一层循环为N次,第二层为V次,遍历k最坏的情况下也要执行j次,因此最坏也取V,总复杂度为
接下来思考如何优化
由
将其枚举:

发现
当前状态的每一项都比上一个状态多一个w[i],既然这样那么最大值也是比上一个状态的最大值多一个w[i]
那么可以得到状态转移方程:
表示:
- 从[0, i -1]中每件物品取无数次,重量不超过j的最大价值
- 从[0, i]中每件物品取无数次,但是重量不超过 j - w (留下再放一件物品的空间)的最大价值
背包容量为 j 时,在考虑放几件第i件物品时,其实在背包容量为j-v[i]时已经考虑过了,在dp[i][j - v[i]]的基础上加上一个w,就是再放一件物品i,能够得到的最大价值,当然有可能不放这件物品i价值最大,这时候最大价值取dp[i - 1][j]。
这样就可以把k这一维度删去,将时间复杂度降为O(NV)
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 1010;
int m, n;
int v[N], w[N], dp[N][N];
int main() {
cin >> m >> n;
for (int i = 1; i <= m; ++i) cin >> v[i] >> w[i];
for (int i = 1; i <= m; ++i)
for (int j = 0; j <= n; ++j) {
dp[i][j] = dp[i - 1][j];
if (j >= v[i])
dp[i][j] = max(dp[i][j], dp[i][j - v[i]] + w[i]);
}
cout << dp[m][n] << endl;
return 0;
}
然后同样可以优化空间复杂度,将dp变为1维
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 1010;
int m, n;
int v[N], w[N], dp[N];
int main() {
cin >> m >> n;
for (int i = 1; i <= m; ++i) cin >> v[i] >> w[i];
for (int i = 1; i <= m; ++i)
for (int j = v[i]; j <= n; ++j)
dp[j] = max(dp[j], dp[j - v[i]] + w[i]);
cout << dp[n] << endl;
return 0;
}
在这里列出01背包和完全背包的递推式进行对比
01背包:
完全背包:
可以看出,因为01背包每件物品只考虑一次,因此添加i物品时背包里不能有i物品,而完全背包每件物品可以添加多次,因此此次添加i物品时,背包里可能还有i物品,所以01背包是由dp[i - 1][j - v] + w 转移而来,而完全背包是由dp[i][j - v]转移来。这也就是为什么01背包遍历背包容量时采用的反向遍历(用上一行的结果推导),而完全背包采用的是正向遍历(用已经更新过的数据推导)
可以得出结论:
- 01背包:每件物品只取一次,反向遍历,dp[i][j] = max(dp[i-1][j], dp[i - 1][j - v] + w
- 完全背包:每件物品取多次,正向遍历,dp[i][j] = max(dp[i-1][j], dp[i][j - v] + w
多重背包
有N种物品和一个容量为V 的背包。第i种物品最多有Mi件可用,每件耗费的空间是Ci ,价值是Wi 。求解将哪些物品装入背包可使这些物品的耗费的空间 总和不超过背包容量,且价值总和最大。
多重背包问题,对每件物品的件数有了限制
例如:背包最大重量为10,表中数据为物品重量、价值、数量,问背包能背的物品最大价值是多少?
| 重量 | 价值 | 数量 | |
|---|---|---|---|
| 物品0 | 1 | 15 | 2 |
| 物品1 | 3 | 20 | 3 |
| 物品2 | 4 | 30 | 2 |
完全背包暴力破解思路
完全背包中每件物品有无数件,多重背包物品件数有限制,因此按照完全背包的思路,在遍历k时加上数量约束即可
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 1010;
int n, V, v[N], w[N], s[N], dp[N][N];
int main(){
cin >> n >> V;
for (int i = 1; i <= n; ++i) cin >> v[i] >> w[i] >> s[i];
for (int i = 1; i <= n; ++i)
for (int j = 0; j <= V; ++j)
for (int k = 0; k <= s[i] && k * v[i] <= j; ++k) // k最多为s[i]件
dp[i][j] = max(dp[i][j], dp[i - 1][j - k * v[i]] + k * w[i]);
cout << dp[n][V] << endl;
return 0;
}
时间复杂度为O(NVS) S是物品件数
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 1010;
int n, V, v[N], w[N], s[N], dp[N];
int main(){
cin >> n >> V;
for (int i = 1; i <= n; ++i) cin >> v[i] >> w[i] >> s[i];
for (int i = 1; i <= n; ++i)
for (int j = V; j >= 0; --j)
for (int k = 0; k <= s[i] && k * v[i] <= j; ++k)
dp[j] = max(dp[j], dp[j - k * v[i]] + k * w[i]);
cout << dp[V] << endl;
return 0;
}
转化为01背包
下面将每件物品的数量限制为1,那么多重背包就转化成了01背包问题
| 重量 | 价值 | 数量 | |
|---|---|---|---|
| 物品0 | 1 | 15 | 1 |
| 物品0 | 1 | 15 | 1 |
| 物品1 | 3 | 20 | 1 |
| 物品1 | 3 | 20 | 1 |
| 物品1 | 3 | 20 | 1 |
| 物品2 | 4 | 30 | 1 |
| 物品2 | 4 | 30 | 1 |
#include <iostream>
#include <cstring>
#include <algorithm>
#include <vector>
using namespace std;
const int N = 1010;
int n, V, dp[N];
int main(){
cin >> n >> V;
int a, b, c;
vector<int> v, w;
for (int i = 1; i <= n; ++i) {
cin >> a >> b >> c;
while (c--) {
v.push_back(a);
w.push_back(b);
}
}
for (int i = 0; i < v.size(); ++i)
for (int j = V; j >= v[i]; --j)
dp[j] = max(dp[j], dp[j - v[i]] + w[i]);
cout << dp[V] << endl;
return 0;
}
- 时间复杂度:O(m n k) m:物品种类个数,n背包容量,k单类物品数量
二进制优化
二进制数转化为十进制数比如:1011 = 2^3 + 0 * 2^2 + 2^1 + 1 = 11
由二进制转化为十进制的算法可以知道,任意一个十进制数x,都可以由(其中
表示不超过x的2的最大次幂)和a(
)表示出来
比如200,可以用1,2,4,8,16,32,64和73表示
证明:1,2,4,8,16,32,64 可表示的范围为 0000000 ~ 1111111 即 0 ~ 127,加上73可以表示的范围为73 ~ 200,那么用1,2,4,8,16,32,64,73可以表示0~200内的任意一个数
因此可以用对物品的个数s[i]分组,分组后转换为01背包问题
时间复杂度由O(NVS)降为O(NVlogS)
分组和加起来不能超过x,因为物品一共就x件
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 24000;
int v[N], w[N], dp[N];
int n, V;
int main() {
cin >> n >> V;
int idx = 0;
for (int i = 1; i <= n; ++i) {
int a, b, c;
cin >> a >> b >> c;
int k = 1;
while (k <= c) {
idx++;
v[idx] = a * k;
w[idx] = b * k;
c -= k;
k *= 2;
}
if (c > 0) {
idx++;
v[idx] = a * c;
w[idx] = b * c;
}
}
n = idx;
for (int i = 1; i <= n; ++i)
for (int j = V; j >= v[i]; --j)
dp[j] = max(dp[j], dp[j - v[i]] + w[i]);
cout << dp[V] << endl;
return 0;
}
分组背包
有N组物品和容量为V的背包,每组物品只能选择一个,求背包最大价值
定义dp[i][j]为从前i组物品中,每组选择不超过一件物品,且容积不超过j的最大价值
那么
完全背包是从一件物品选k件,分组背包是从k件物品中选1件,那么只需要枚举这k件取最大值即可
因为每次更新用的是上一行的数据,因此遍历背包体积时从大到小遍历
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 110;
int n, V;
int v[N][N], w[N][N], s[N], dp[N];
int main() {
cin >> n >> V;
for (int i = 1; i <= n; ++i) {
cin >> s[i];
for (int j = 1; j <= s[i]; ++j) cin >> v[i][j] >> w[i][j];
}
for (int i = 1; i <= n; ++i) // 枚举组
for (int j = V; j >= 0; --j) // 枚举背包体积
for (int k = 1; k <= s[i]; ++k) // 选择每组的第k件
if (j >= v[i][k])
dp[j] = max(dp[j], dp[j - v[i][k]] + w[i][k]);
cout << dp[V] << endl;
return 0;
}


