面试题 02.07. 链表相交

思路一：迭代

本来很简洁明了的一道题，让题目描述搞的云里雾里的。
简单来说，就是求两个链表交点节点的指针。 这里要注意，交点不是数值相等，而是指针相等。
为了方便举例，假设节点元素数值相等，则节点指针相等。
看如下两个链表，目前curA指向链表A的头结点，curB指向链表B的头结点：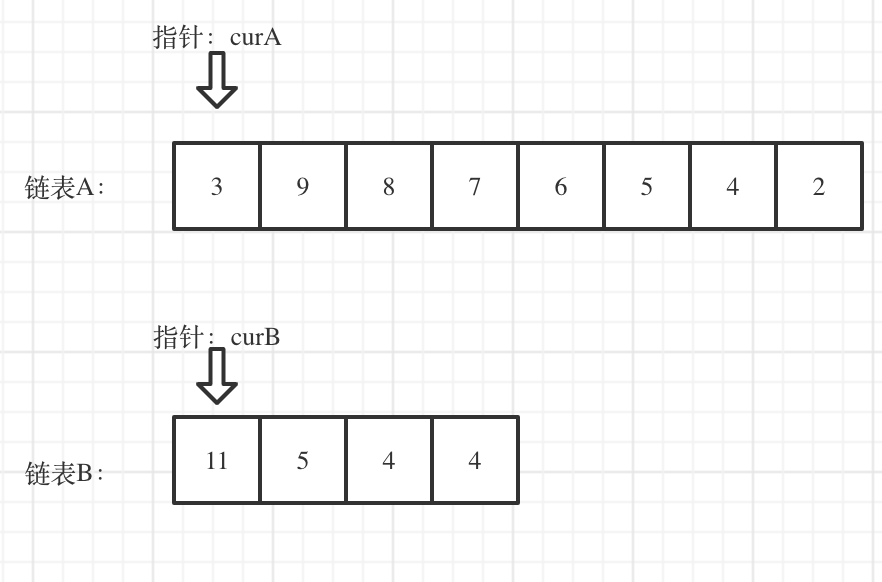
链表相交 - 图1
我们求出两个链表的长度，并求出两个链表长度的差值，然后让curA移动到，和curB 末尾对齐的位置，如图：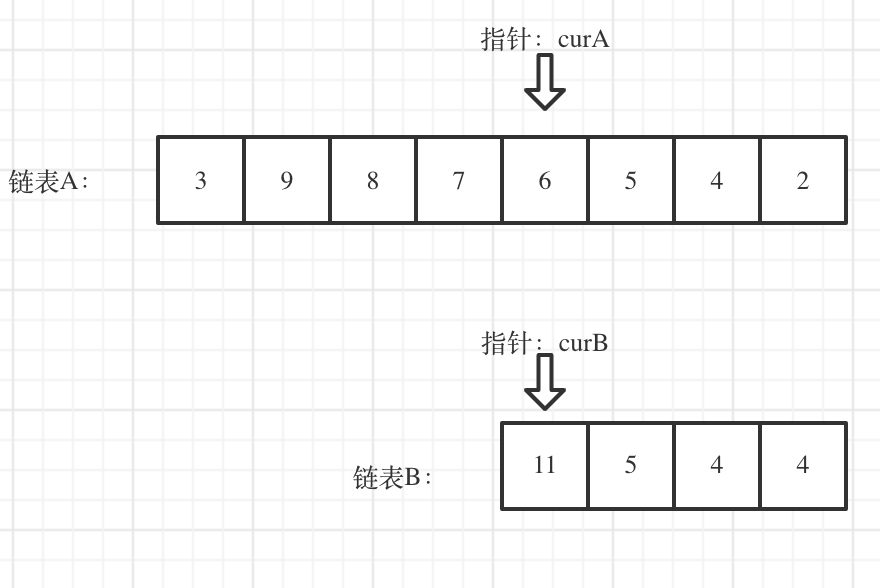
链表相交 - 图2
此时我们就可以比较curA和curB是否相同，如果不相同，同时向后移动curA和curB，如果遇到curA == curB，则找到交点。
否则循环退出返回空指针。

  1. /**
  2.  * Definition for singly-linked list.
  3.  * struct ListNode {
  4.  *     int val;
  5.  *     ListNode *next;
  6.  *     ListNode(int x) : val(x), next(NULL) {}
  7.  * };
  8.  */
  9. class Solution {
  10. public:
  11.     ListNode *getIntersectionNode(ListNode *headA, ListNode *headB) {
  12.         ListNode* curA = headA;
  13.         ListNode* curB = headB;
  14.         int lenA = 0, lenB = 0;
  15.         while (curA != NULL) { // 求链表A的长度
  16.             lenA++;
  17.             curA = curA->next;
  18.         }
  19.         while (curB != NULL) { // 求链表B的长度
  20.             lenB++;
  21.             curB = curB->next;
  22.         }
  23.         curA = headA;
  24.         curB = headB;
  25.         // 让curA为最长链表的头，lenA为其长度
  26.         if (lenB > lenA) {
  27.             swap (lenA, lenB);
  28.             swap (curA, curB);
  29.         }
  30.         // 求长度差
  31.         int gap = lenA - lenB;
  32.         // 让curA和curB在同一起点上（末尾位置对齐）
  33.         while (gap--) {
  34.             curA = curA->next;
  35.         }
  36.         // 遍历curA 和 curB，遇到相同则直接返回
  37.         while (curA != NULL) {
  38.             if (curA == curB) {
  39.                 return curA;
  40.             }
  41.             curA = curA->next;
  42.             curB = curB->next;
  43.         }
  44.         return NULL;
  45.     }
  46. };

思路二：双指针

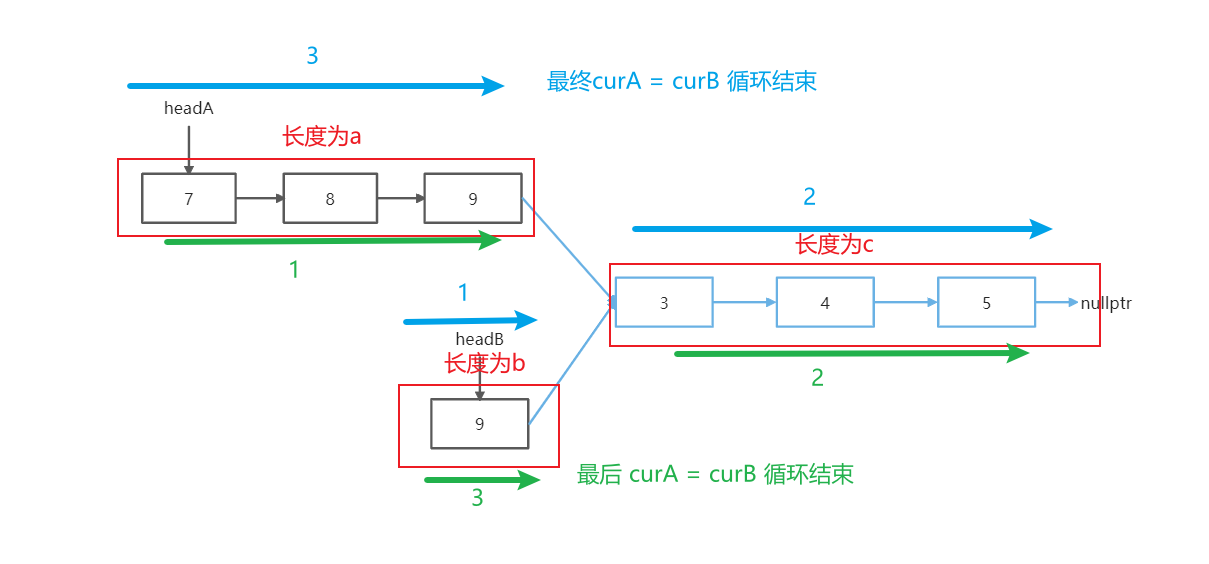
假设链表一除了相交部分的长度为a，链表二除了相交部分的长度为b，相交部分长度为c
则 a + c + b = b + c + a,如果不想交的话a + b = b + a,也就是说两个指针都扫描a+b+c个节点后，最终会指向交点，如果不存在交点，最终都指向NULL

链表相交 - 图3

image.png

  1. /**
  2.  * Definition for singly-linked list.
  3.  * struct ListNode {
  4.  *     int val;
  5.  *     ListNode *next;
  6.  *     ListNode(int x) : val(x), next(NULL) {}
  7.  * };
  8.  */
  9. class Solution {
  10. public:
  11.     ListNode *getIntersectionNode(ListNode *headA, ListNode *headB) {
  12.         ListNode* curA = headA;
  13.         ListNode* curB = headB;
  14.         while (curA != curB) {
  15.             curA = curA == NULL ? headB : curA->next;
  16.             curB = curB == NULL ? headA : curB->next;
  17.         }
  18.         return curA;
  19.     }
  20. };

时间复杂度O(M+N)
空间复杂度O(1)

思路三：哈希

先遍历链表A，并将所有节点存入集合，然后遍历链表B，碰到第一个存在于集合中的节点，就是第一个相交的节点，如果集合中没有，返回NULL

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode(int x) : val(x), next(NULL) {}
 * };
 */
class Solution {
public:
    ListNode *getIntersectionNode(ListNode *headA, ListNode *headB) {
        unordered_set<ListNode*> us;
        ListNode* cur = headA;
        while (cur) {
            us.insert(cur);
            cur = cur->next;
        }
        cur = headB;
        while (cur) {
            if (us.count(cur)) {
                return cur;
            }
            cur = cur->next;
        }
        return NULL;
    }
};

时间复杂度O(M+N)
空间复杂度O(M)