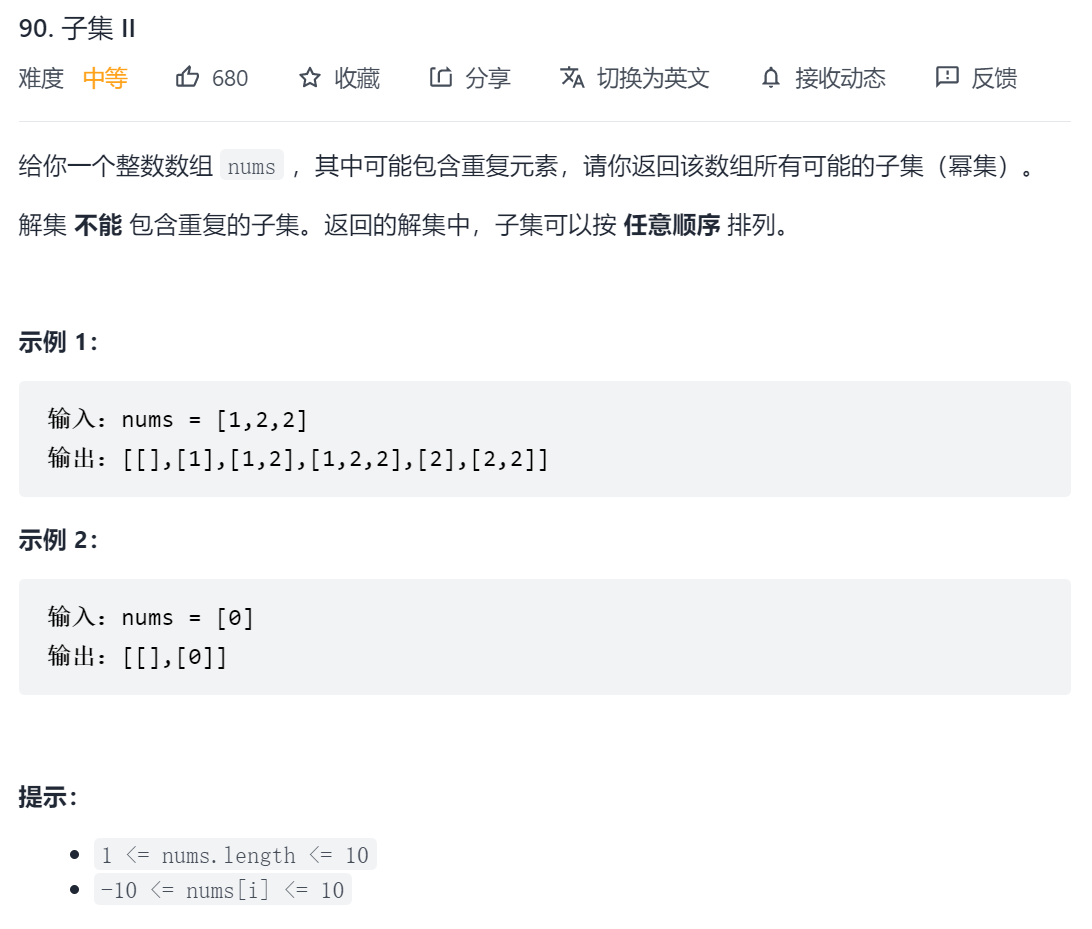
78. 子集

image.png

回溯

子集问题和组合问题类似，可以先从集合的元素中按照顺序选择，然后递归处理余下的元素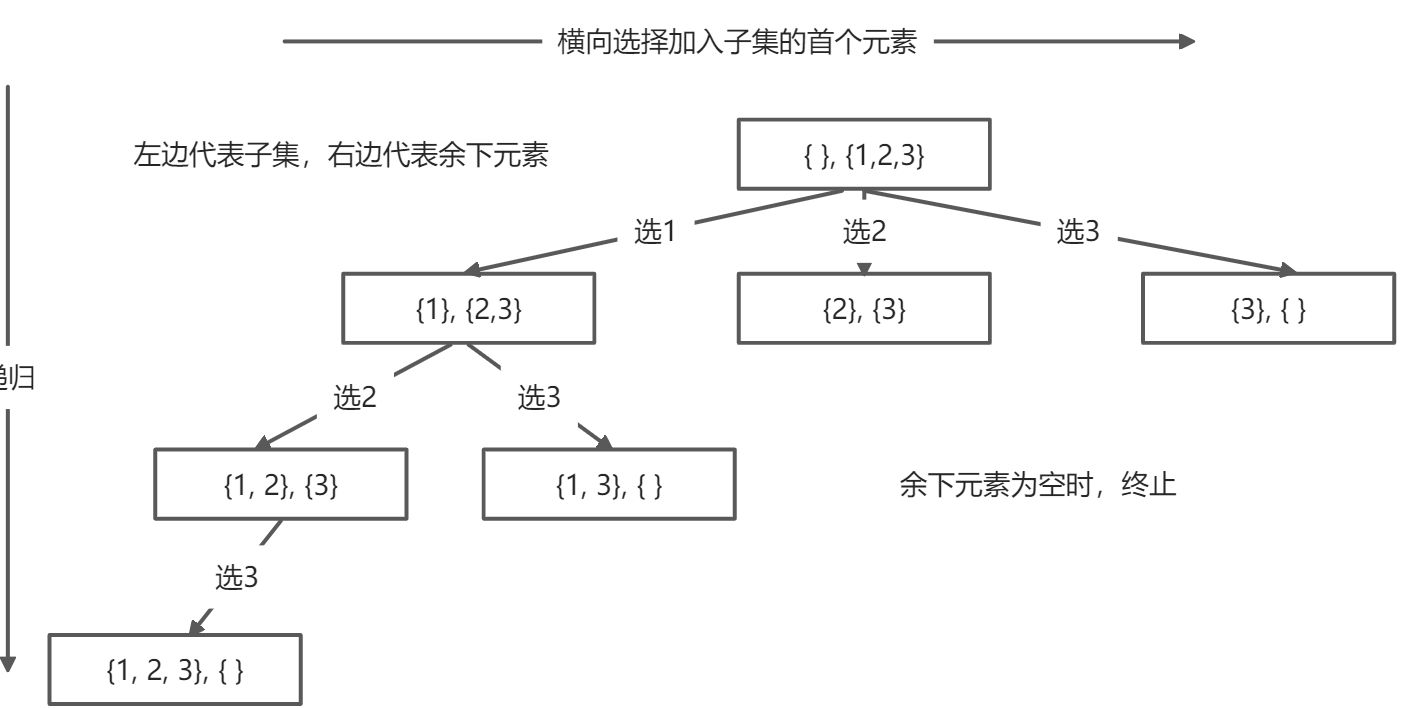
子集问题 - 图2
回溯三部曲

  1. 参数

要处理的数组
startIndex起始元素，此次要加入子集的元素索引

  1. 终止条件

startIndex达到数组大小时，表示已经无元素可以加入到子集，return

  1. if (startIndex >= nums.size())
  2.     return;

for循环中已经判断了startIndex，其实不加终止条件也可以

  1. 单层递归的逻辑

将startIndex指向的元素加入path中，递归处理余下的部分，回溯，然后continue。

  1.         for (int i = startIndex; i < nums.size(); i++) {
  2.             path.push_back(nums[i]); // 将当前元素加入子集
  3.             backtracking(nums, i + 1); //处理[i + 1, nums.size()-1]
  4.             path.pop_back();
  5.         }

完整代码：

  1. class Solution {
  2. public:
  3.     vector<vector<int>> res;
  4.     vector<int> subset;
  5.     void dfs(vector<int>& nums, int start) {
  6.         res.push_back(subset); // 空集也是子集
  7.         if (start >= nums.size()) return;
  8.         for (int i = start; i < nums.size(); ++i) {
  9.             subset.push_back(nums[i]);
  10.             dfs(nums, i + 1);
  11.             subset.pop_back();
  12.         }
  13.     }
  14.     vector<vector<int>> subsets(vector<int>& nums) {
  15.         dfs(nums, 0);
  16.         return res;
  17.     }
  18. };

二进制位运算

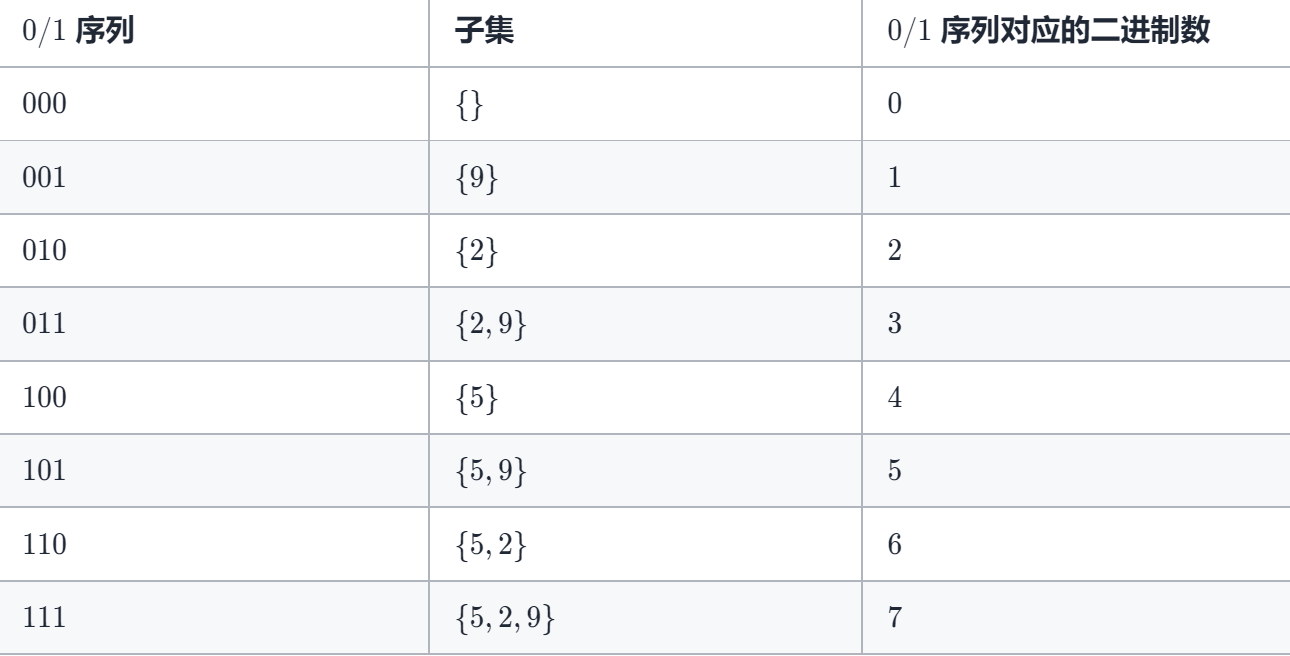
image.png
用二进制选择取子集的哪一个元素，位是1，则取对应位置的元素，位是0，则不取
子集个数一个 2^n 个，所以循环的次数为 2^n 次：每次循环中，将1位对应的元素加入到子集中

  1. class Solution {
  2. public:
  3.     vector<vector<int>> subsets(vector<int>& nums) {
  4.         vector<vector<int>> result;
  5.         vector<int> subset;
  6.         int n = nums.size();
  7.         for (int mask = 0; mask < (1 << n); mask++) {
  8.             subset.clear();
  9.             for (int i = 0; i < n; i++) {
  10.                 if (mask & (1 << i)) {// 如果在二进制中i对应的位置为1，则加入子集
  11.                     subset.push_back(nums[i]);
  12.                 } 
  13.             }
  14.             result.push_back(subset);
  15.         }
  16.         return result;
  17.     }
  18. };

image.png位运算迭代法，快的一批！

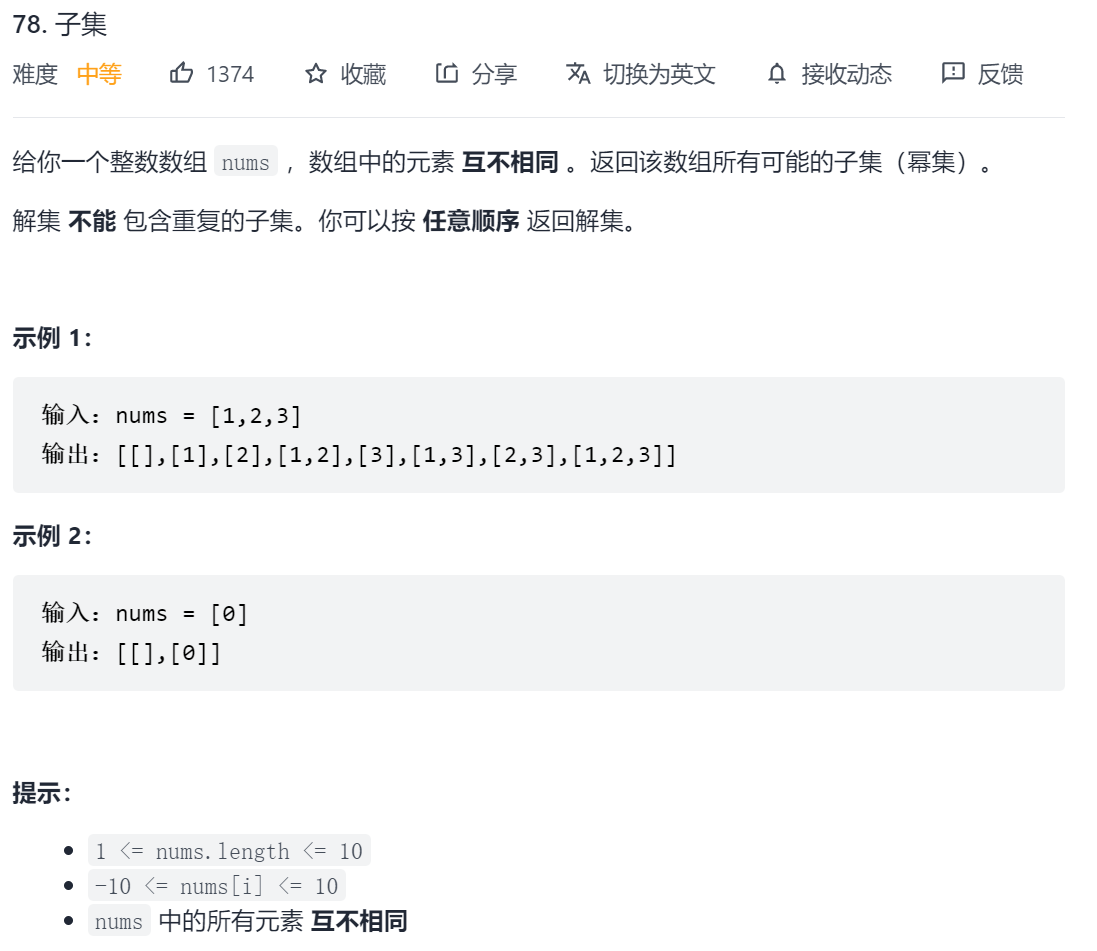
90. 子集 II

image.png

回溯

想一下组合问题有重复元素是怎么处理的，先排序，然后横向遍历时，如果nums[i] = nums[i - 1]，那么continue
组合、子集、排列去重都是这个套路，理解树枝去重和树层去重很重要。

class Solution {
public:
    vector<vector<int>> result;
    vector<int> path;
    void backtracking(vector<int>& nums, int startIndex) {
        result.push_back(path);
        if (startIndex >= nums.size())
            return;
        for (int i = startIndex; i < nums.size(); i++) {
            if (i > startIndex && nums[i] == nums[i - 1])
                continue;
            path.push_back(nums[i]);
            backtracking(nums, i + 1);
            path.pop_back();
        }
    }
    vector<vector<int>> subsetsWithDup(vector<int>& nums) {
        sort(nums.begin(), nums.end());
        backtracking(nums, 0);
        return result;
    }
};

二进制迭代

先套用78题的代码，然后增加去重逻辑
考虑数组 [1,2,2]，选择前两个数，或者第一、三个数，都会得到相同的子集。
也就是说，对于当前选择的数 x，若前面有与其相同的数 y，且没有选择 y，此时包含 x 的子集，必然会出现在包含 y 的所有子集中。
我们可以通过判断这种情况，来避免生成重复的子集。代码实现时，可以先将数组排序；迭代时，若发现没有选择上一个数，且当前数字与上一个数相同，则可以跳过当前生成的子集。

class Solution {
public:
    vector<int> t;
    vector<vector<int>> ans;

    vector<vector<int>> subsetsWithDup(vector<int> &nums) {
        sort(nums.begin(), nums.end());
        int n = nums.size();
        for (int mask = 0; mask < (1 << n); ++mask) {
            t.clear();
            bool flag = true;
            for (int i = 0; i < n; ++i) {
                if (mask & (1 << i)) {
                    if (i > 0 && (mask >> (i - 1) & 1) == 0 && nums[i] == nums[i - 1]) {
                        flag = false;
                        break;
                    }
                    t.push_back(nums[i]);
                }
            }
            if (flag) {
                ans.push_back(t);
            }
        }
        return ans;
    }
};

491. 递增子序列

image.png

寻找递增子序列，给的数组nums不能排序后再处理，因此不能用带重复元素的组合子集中的那种去重逻辑，可以用哈希表来记录当前元素是否在同一层使用过。

子序列最少含有两个元素，当path.size() > 1 时，保存结果

if (path.size() > 1)
    result.push_back(path);

先判断该层是否使用过这个数值：

  • 使用过：continue
  • 没使用过：如果path不空，并且当前元素大于等于path.back()，将其加入子序列中

题目给定的数值范围为-100 <= x <= 100，那么显然可以用一个数组来记录元素是否使用过，新建数组，默认值都是0，如果用过，给它置为1，省去了遍历的过程

class Solution {
public:
    vector<vector<int>> res;
    vector<int> seq;
    void dfs(vector<int>& nums, int start) {
        if (seq.size() > 1) { // 子序列最少两个，当元素个数满足要求时，保存结果
            res.push_back(seq);
        }
        bool hash[201] = {false};
        for (int i = start; i < nums.size(); ++i) { // 处理当前层，选择递增子序列某个位置的元素
            if (hash[nums[i] + 100] || (!seq.empty() && nums[i] < seq.back())) continue;
            hash[nums[i] + 100] = true;
            seq.push_back(nums[i]);
            dfs(nums, i + 1); // 查找下一个元素
            seq.pop_back(); // 回溯，这一个位置为nums[i]的所有子序列查找完毕，下一次for循环将更新此位置的值
        }

    }
    vector<vector<int>> findSubsequences(vector<int>& nums) {
        dfs(nums, 0);
        return res;
    }
};

image.png速度对比。

注：本题也可以归类为深度优先搜索（DFS）