27. 移除元素

双指针法：
一个指针用来遍历，一个指针用来记录移动的位置，每当nums[i] == val时，j++，否则将元素向前移动 j 个单位，最后返回的 nums.size() - j

class Solution {
public:
    int removeElement(vector<int>& nums, int val) {
        int n = nums.size();
        int i = 0, j = 0;
        while(i < n) {
            if (nums[i] == val) 
                j++;
            else {
                nums[i - j] = nums[i];
            }
            i++;
        }
        return n - j;
    }
};

双指针快慢指针：快指针用来遍历，慢指针用来记录元素移动的位置

// 时间复杂度：O(n)
// 空间复杂度：O(1)
class Solution {
public:
    int removeElement(vector<int>& nums, int val) {
        if (nums.size() == 0) return 0;
        int slow = 0;
        for (int fast = 0; fast < nums.size(); ++fast) {
            if (nums[fast] != val) {
                nums[slow++] = nums[fast];
            }
        }
        return slow;
    }
};

26. 删除有序数组中的重复项

双指针法，fast遍历数组，slow记录待保留元素的位置，就是最后要求数组的下标，循环结束后slow应该是最后一个元素的下标，因此数组长度为slow+1

class Solution {
public:
    int removeDuplicates(vector<int>& nums) {
        if(nums.size() == 0) return 0;
        int slow = 0;
        for(int fast = 1; fast < nums.size(); ++fast)
            if(nums[slow] != nums[fast]) // 和慢指针指向的元素比较
                nums[++slow] = nums[fast]; // 如果不同，那么增加一个元素，slow先—+1再赋值
        // slow 为处理后的数组的最后一个元素下标，数组长度为slow+1        
        return slow + 1;
    }
};

80. 删除有序数组中的重复项 II

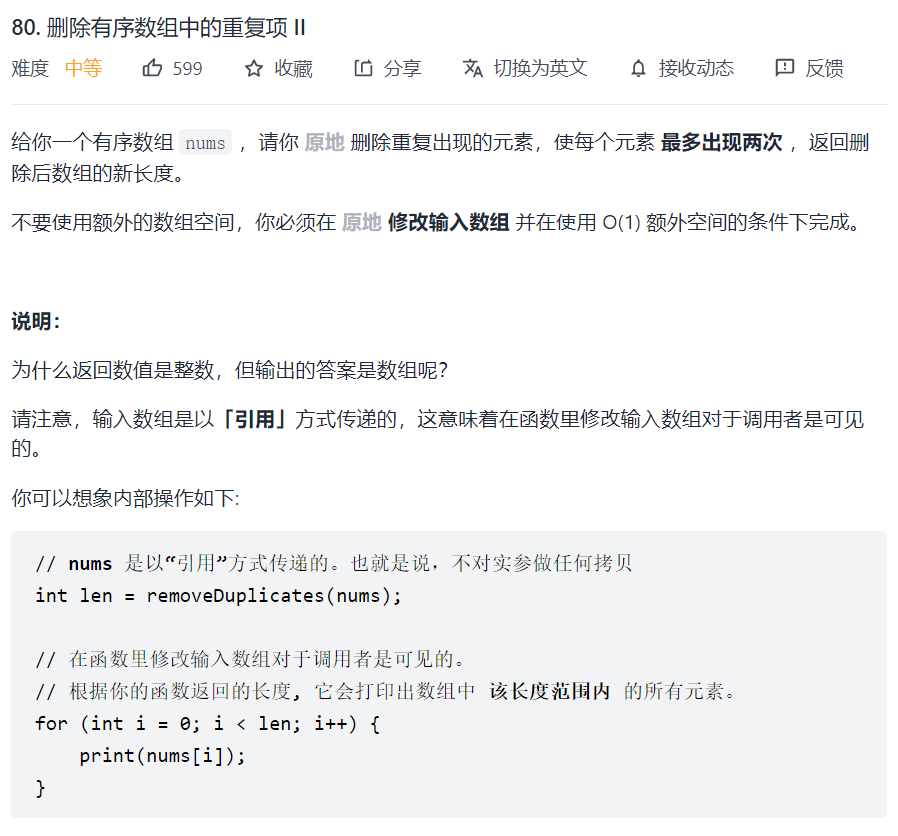
解法：参照（LeetCode26题），

class Solution {
public:
  int removeDuplicates(vector<int>& nums) {
      if (nums.size() < 2) return nums.size();
      int slow = 2;
      for (int fast = 2; fast < nums.size(); ++fast) {
          // 元素可以出现两次，所以快指针和慢指针的前两个元素进行比较即可
          if (nums[slow - 2] != nums[fast]) {
              nums[slow++] = nums[fast];
          }
      }
      return slow;
  }
};

283. 移动零

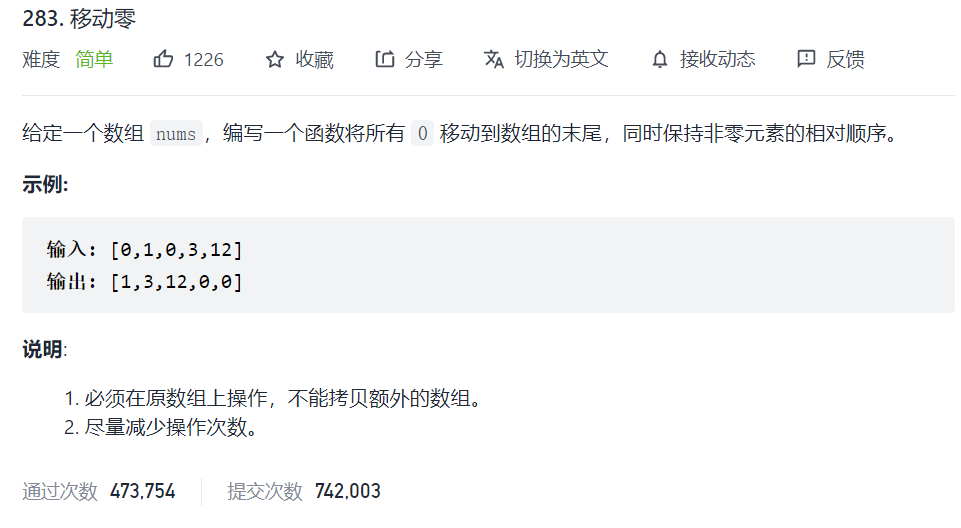
这道题很简单，
思路一：先把零删了再补零
用两个指针，把所有的非零元素都移至数组前方，前半部分的下标由慢指针来记录，快指针用来遍历数组，然后将slow到 nums.size()之间的所有元素填充为零即可

class Solution {
public:
  void moveZeroes(vector<int>& nums) {
      int slow = 0;
      for (int fast = 0; fast < nums.size(); ++fast) {
          if (nums[fast] != 0)
              nums[slow++] = nums[fast];
      }

      for (int i = slow; i < nums.size(); ++i) {
          nums[i] = 0;
      }
  }
};

思路二：使用双指针，左指针指向当前已经处理好的序列的尾部，右指针指向待处理序列的头部。
右指针不断向右移动，每次右指针指向非零数，则将左右指针对应的数交换，同时左指针右移。
注意到以下性质：

左指针左边均为非零数；
右指针左边直到左指针处均为零。

因此每次交换，都是将左指针的零与右指针的非零数交换，且非零数的相对顺序并未改变。
这种解法的好处是可以不使用补零循环，比较省时间

class Solution {
public:
    void moveZeroes(vector<int>& nums) {
        int left = 0;
        for (int right = 0; right < nums.size(); ++right) {
            if (nums[right] != 0) {
                swap(nums[right], nums[left++]);
            }
        }
    }
};

844. 比较含退格的字符串

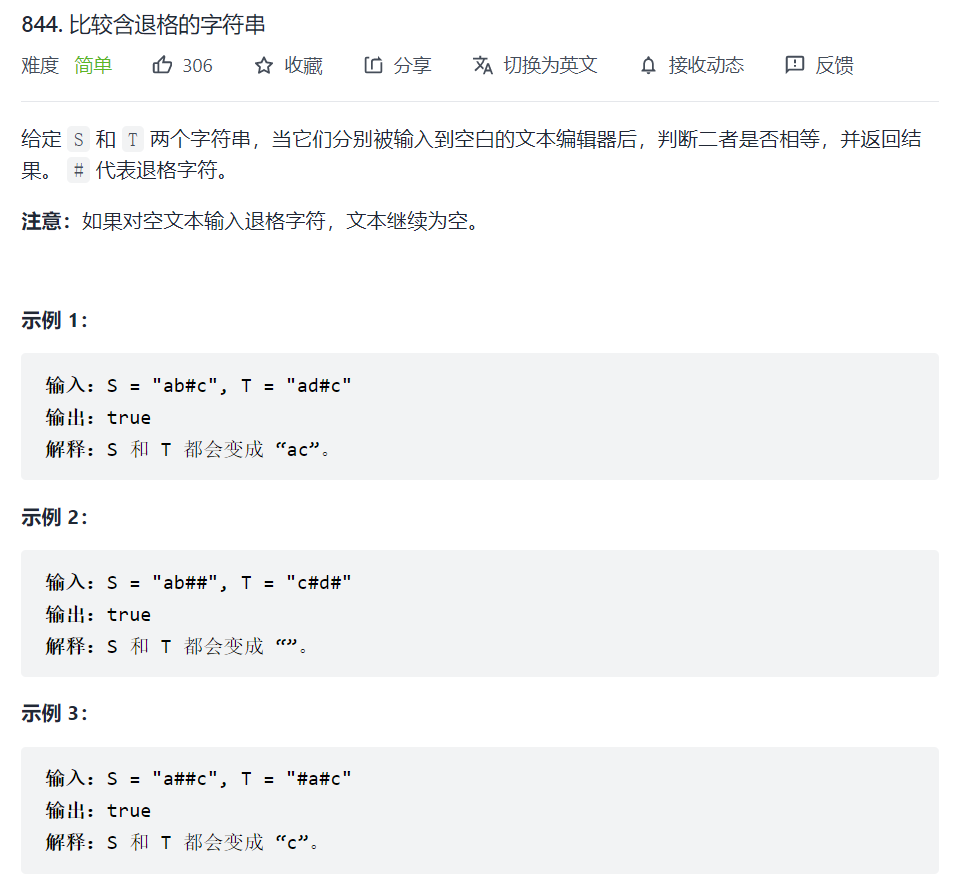
思路1：双指针
首先定义一个函数用来处理字符串，和删除元素类似，双指针，快指针来扫描字符串，慢指针指向处理字符串的末尾后一个位置
与删除元素不同的时，每当遇到 # ，慢指针需要回退一个，除非慢指针指向0

class Solution {
public:
    bool backspaceCompare(string s, string t) {
        int len1 = dealStr(s), len2 = dealStr(t);
        if (len1 != len2)
            return false;
        for (int i = 0; i < len1; ++i) {
            if (s[i] != t[i])
                return false;

        }
        return true;
    }

    int dealStr(string &s) {
        int slow = 0;
        for (int fast = 0; fast < s.size(); ++fast) {
            if (s[fast] != '#') {
                s[slow++] = s[fast];
            } else {
                if (slow > 0) slow--;
            }
        }
        return slow;
    }
};

思路二：栈
每当碰到‘#’时，如果栈不为空，则弹出栈顶元素，否则将元素压入栈中

class Solution {
public:
    bool backspaceCompare(string s, string t) {
        return dealStr(s) == dealStr(t);
    }

    string dealStr(string &s) {
        string str;
        for (auto & c : s) {
            if (c != '#')
                str.push_back(c);
            else if (!str.empty())
                str.pop_back();
        }
        return str;
    }
};

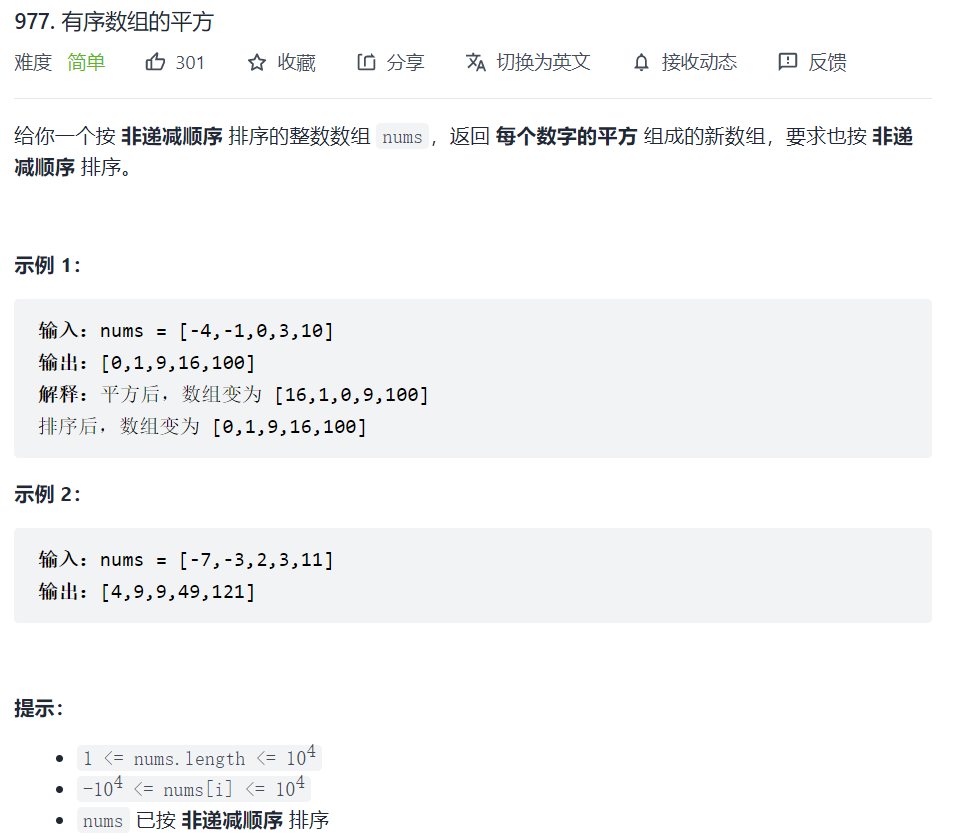
977. 有序数组的平方

思路一：直接平方后排序

class Solution {
public:
    vector<int> sortedSquares(vector<int>& nums) {
        for (auto& num : nums) num *= num;
        sort(nums.begin(), nums.end());
        return nums;
    }
};
// class Solution {
// public:
//     vector<int> sortedSquares(vector<int>& nums) {
//         for (int i = 0; i < nums.size(); i++) {
//             nums[i] = nums[i] * nums[i];
//         }
//         sort(nums.begin(), nums.end());
//         return nums;
//     }
// };

时间复杂度O(nlogn) 为排序的复杂度
空间复杂度都为O(1)

思路二：归并

找到正负的分界线，然后用类似于归并排序的方法处理

class Solution {
public:
    vector<int> sortedSquares(vector<int>& nums) {
        int negative = -1, n = nums.size();//如果最后negative仍是负数，说明没有负数
        for (int i = 0; i < n; ++i) {
            if (nums[i] >= 0) break;
            else negative++;
        }
        vector<int> ans(n);
        int pos = 0, noNegative = negative + 1;//noNegative记录第一个非负数的下标
        while (negative >= 0 && noNegative < n) {
            if (nums[negative] * nums[negative] <= nums[noNegative] * nums[noNegative]) {
                ans[pos++] = nums[negative] * nums[negative];
                negative--;
            }  
            else {
                ans[pos++] = nums[noNegative] * nums[noNegative];
                noNegative++;
            }        
        }
        while (negative >= 0) {
            ans[pos++] = nums[negative] * nums[negative];
                negative--;
        }
        while (noNegative < n) {
            ans[pos++] = nums[noNegative] * nums[noNegative];
                noNegative++;
        }
        return ans;
    }
};

思路三：双指针

一个指针指向数组头，一个指针指向数组尾，每次选择平方较大者插入新的数组

class Solution {
public:
    vector<int> sortedSquares(vector<int>& nums) {
        int left = 0, right = nums.size() - 1, index = right;
        vector<int> ans(nums.size());
        while (left <= right) {
            if (nums[right] * nums[right] <= nums[left] * nums[left]) {
                ans[index--] = nums[left] * nums[left];
                ++left;
            } else {
                ans[index--] = nums[right] * nums[right];
                --right;
            }
        }
        return ans;
    }
};