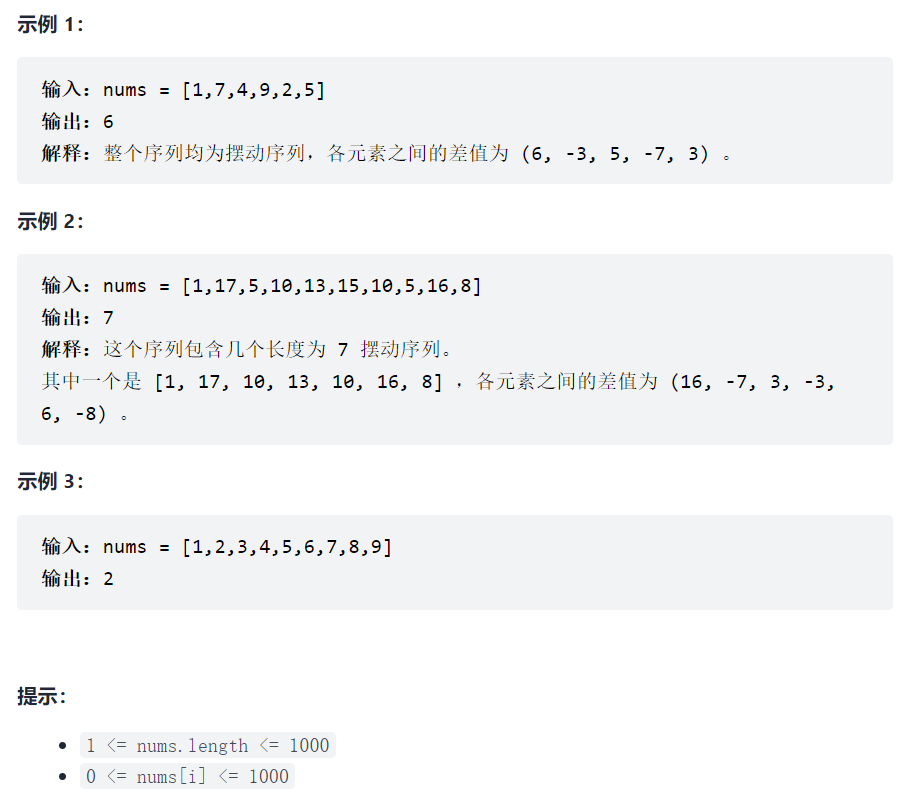
376. 摆动序列💦

思路一：动态规划

记最后一个元素呈上升趋势的摆动子序列为上升摆动序列
最后一个元素呈下降趋势的摆动子序列为下降摆动序列
用数组up[i]记录以前i各元素中某几个为结尾的最长上升摆动序列的长度
用数组down[i]记录以前i各元素中某几个为结尾的最长下降摆动序列的长度

分析up：

• 当nums[i] <= nums[i - 1]时，以nums[i]为结尾的上升摆动序列的结尾都可以用nums[i - 1]来替换，因此up[i] = up[i - 1]
• 当nums[i] > nums[i - 1]时：
  • 从down[i - 1]转移：一定存在前i - 1个元素中的最长下降摆动序列的最后一个元素小于num[i]，那么加上nums[i]这个元素可以组成一个长度为down[i - 1] + 1的上升摆动序列
  • 从up[i - 1]转移：假如上升摆动序列的最后一个元素小于nums[i]，那么长度不变；最后一个元素大于nums[i]，要继续保持为上升摆动序列，最后一个元素不改变，长度保持不变，有up[i] = up[i - 1]

同理可以分析出down[i]的转移方程。

综上所述，有状态转移方程：

代码：

class Solution {
public:
    int wiggleMaxLength(vector<int>& nums) {
        int n = nums.size();
        if (n < 2) return n;
        vector<int> up(n), down(n);
        up[0] = down[0] = 1;
        for (int i = 1; i < n; i++) {
            if (nums[i] > nums[i - 1]) {
                up[i] = max(up[i - 1], down[i - 1] + 1);
                down[i] = down[i - 1];
            } else if (nums[i] < nums[i - 1]){
                up[i] = up[i - 1];
                down[i] = max(up[i - 1] + 1, down[i - 1]);
            } else {
                up[i] = up[i - 1];
                down[i] = down[i - 1];
            }
        }
        return max(up[n - 1], down[n - 1]);
    }
};

复杂度分析：

• 时间复杂度O(N)
• 空间复杂度O(N)

因为每次更新只需要前一个数据，可以维护两个变量来代替数组

class Solution {
public:
    int wiggleMaxLength(vector<int>& nums) {
        int n = nums.size();
        if (n < 2) return n;
        int up = 1, down = 1;
        for (int i = 1; i < n; i++) {
            if (nums[i] > nums[i - 1]) {
                up = max(up, down + 1);
            } else if (nums[i] < nums[i - 1]){
                down = max(up + 1, down);
            }
        }
        return max(up, down);
    }
};

复杂度分析：

• 时间复杂度O(N)
• 空间复杂度O(1)

  思路二：贪心

  统计峰和谷的个数即可

  class Solution {
  public:
    int wiggleMaxLength(vector<int>& nums) {
        int n = nums.size();
        if (n < 2) return n;
        int pre = nums[1] - nums[0];
        int res = pre ? 2 : 1; // 如果前两个元素相等，初始化为1，二者取一
        for (int i = 2; i < n; i++) {
            int cur = nums[i] - nums[i - 1];
            // 如果发生摆动，那么增加计数
            // 前一个高度差为0，那么无论当前高度差的正负结果都会增加一个
            if ((pre <= 0 && cur > 0) || (pre >= 0 && cur < 0)) {
                res++;
                pre = cur;
            }
        }
        return res;
    }
  };
  

53. 最大子序和

暴力解法

第一层for设置起始位置，第二层for循环遍历数组寻找最大值
时间复杂度：O(n^2) 空间复杂度：O(1) (超时)

class Solution {
public:
    int maxSubArray(vector<int>& nums) {
        int result = INT32_MIN;
        int count = 0;
        for (int i = 0; i < nums.size(); i++) {
            count = 0;
            for (int j = i; j < nums.size(); j++) {
                count += nums[j];
                result = max(result, count);
            }
        }
        return result;
    }
};

贪心

前面的和如果是正的，那么累加，如果是负的，那么就扔掉它自立门户

class Solution {
public:
    int maxSubArray(vector<int>& nums) {
        if (nums.empty()) return 0;
        int res = nums[0], sum = nums[0];
        for (int i = 1; i < nums.size(); i++) {
            sum = sum > 0 ? sum + nums[i] : nums[i];
            res = max(res, sum);
        }
        return res;
    }
};

class Solution {
public:
    int maxSubArray(vector<int>& nums) {
        int result = INT32_MIN;
        int count = 0;
        for (int i = 0; i < nums.size(); i++) { // 设置起始位置
            count += nums[i];
            result = max(count, result);// result 记录最大的子序和
            if (count <= 0) // 当前连续子序列的和为负数或者0了
                count = 0; // 重置累计和
        }
        return result;
    }
};

动态规划

假设nums数组的长度为n，下标范围为0 ~ n-1
可以设f(i)为以nums[i]为结尾的最大子序和，用dp数组来存储f(i)的值，那么最后的结果应该是dp数组的最大值，dp[i]的状态转移方程为

class Solution {
public:
    int maxSubArray(vector<int>& nums) {
        int n = nums.size();
        if (n == 1) return nums[0]; // nums.length >= 1

        vector<int> dp(n, 0);
        dp[0] = nums[0];
        for (int i = 1; i < n; ++i) {
            dp[i] = max(nums[i], dp[i - 1] + nums[i]);
        }

        return *max_element(dp.begin(), dp.end());
    }
};

将空间复杂度由O(n)减小为O(1)

class Solution {
public:
    int maxSubArray(vector<int>& nums) {
        int n = nums.size();
        if (n == 1) return nums[0]; // nums.length >= 1
        int res = nums[0];
        int pre = 0;
        for (int i = 0; i < n; ++i) {
            pre = max(nums[i], pre + nums[i]);
            res = max(res, pre);
        }
        return res;
    }
};

或者

class Solution {
public:
    int maxSubArray(vector<int>& nums) {
        int pre = 0, res = nums[0];
        for (const auto & num : nums) {
            pre = max(num, pre + num);
            res = max(res, pre);
        }
        return res;
    }
};

2021.11.10日更新
测试样例应该是更新了，和两个月前的结果差距有点大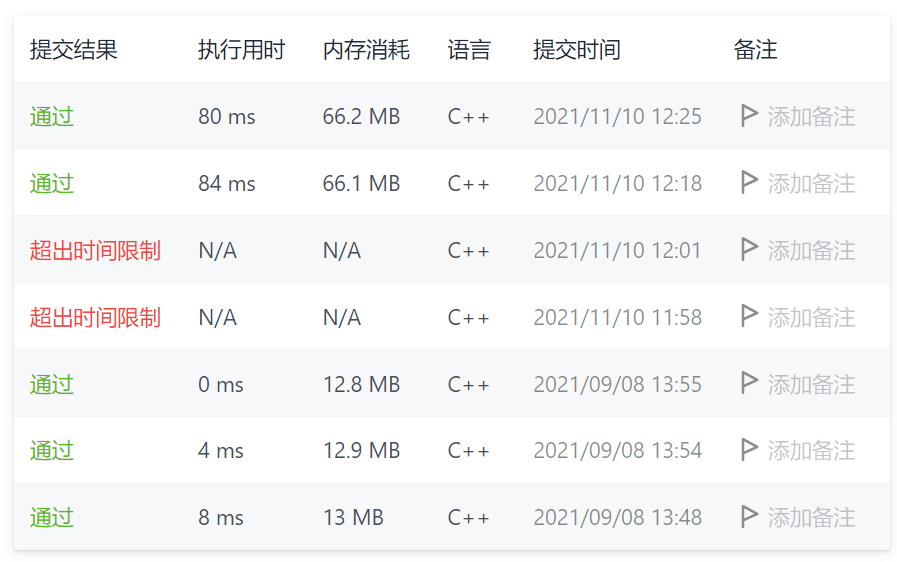

1005. K 次取反后最大化的数组和

按绝对值排序

贪心策略，要想最后的数组和最大，要尽可能的取反绝对值大的负数和绝对值小的正数，这样才能使最后的和最大
那么可以先将数组按照绝对值从大到小排序，然后遍历数组，当遇到负数的时候就给他取反（排序后先取反的一定是绝对值大的）
如果把所有负数都取反了，k还没用完，有两种情况：

• 如果k是偶数，来回翻转能够保证最后数仍是正的，所以不用动
• 如果k是奇数，那么将绝对值最小的正数取反一次即可

class Solution {
public:
    int largestSumAfterKNegations(vector<int>& nums, int k) {
        sort(nums.begin(), nums.end(), [](int& a, int& b){ return abs(a) > abs(b);});
        for (auto & num : nums) { // 这里使用引用很重要，不然不会改变原数组的值
            if (num < 0 && k >0) {
                num *= -1;
                k--;
            }
        }
        if (k % 2 == 1) nums[nums.size() - 1] *= -1;
        int sum = 0;
        for (auto num : nums)
            sum += num;
        return sum;
    }
};

升序排序

直接从小到大排序，绝对值大的负数在左边，优先反转左边元素，如果所有负数反转完毕，k还未用完且为奇数，那么反转最小整数（可以用一个索引来记录最小正数的位置，当然反转完负数后要更新一下，有可能反转后的负数比原来的那个正数小）

class Solution {
public:
    int largestSumAfterKNegations(vector<int>& nums, int k) {
        int n = nums.size();
        sort(nums.begin(), nums.end());
        int idx = 0;
        while (idx < n && nums[idx] < 0) idx++; // 找到第一个非负数
        for (int i = 0; i < idx && k; i++) {
            nums[i] *= -1;
            k--;
        }
        if (k % 2 != 0) {
            // 所有负数变正了，k有剩余，更新一下最小整数，然后将其反转
            // 如果原本数组都是负的，或者反转后出现更小正数
            if ((idx > 0 && nums[idx - 1] < nums[idx]) || idx == n) idx--;
            nums[idx] *= -1;
        }
        return accumulate(nums.begin(), nums.end(), 0);
    }
};