106. 从中序与后序遍历序列构造二叉树

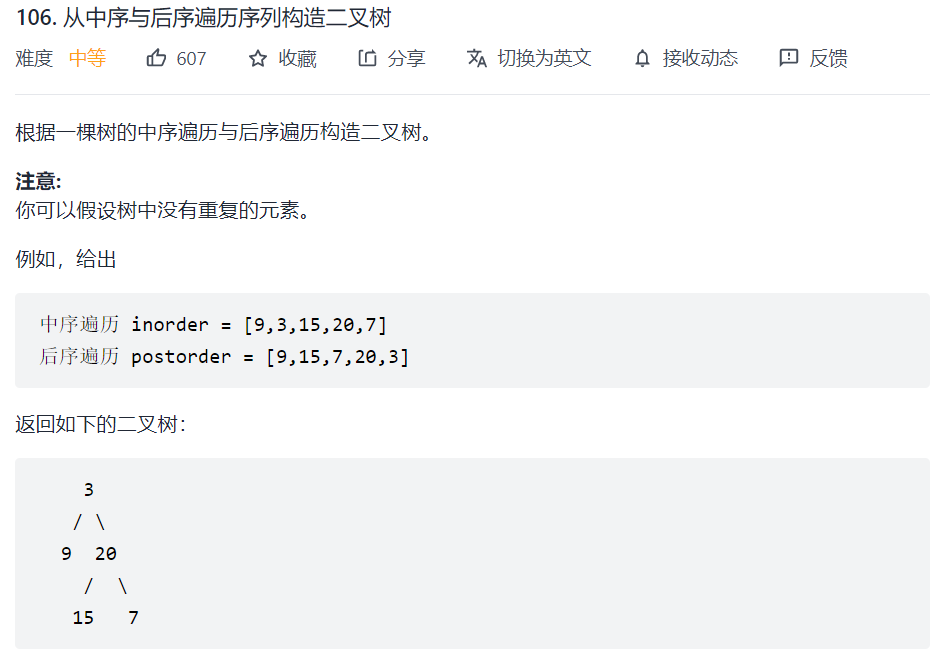
image.png
以 后序数组的最后一个元素为切割点，先切中序数组，根据中序数组，反过来在切后序数组。一层一层切下去，每次后序数组最后一个元素就是节点元素。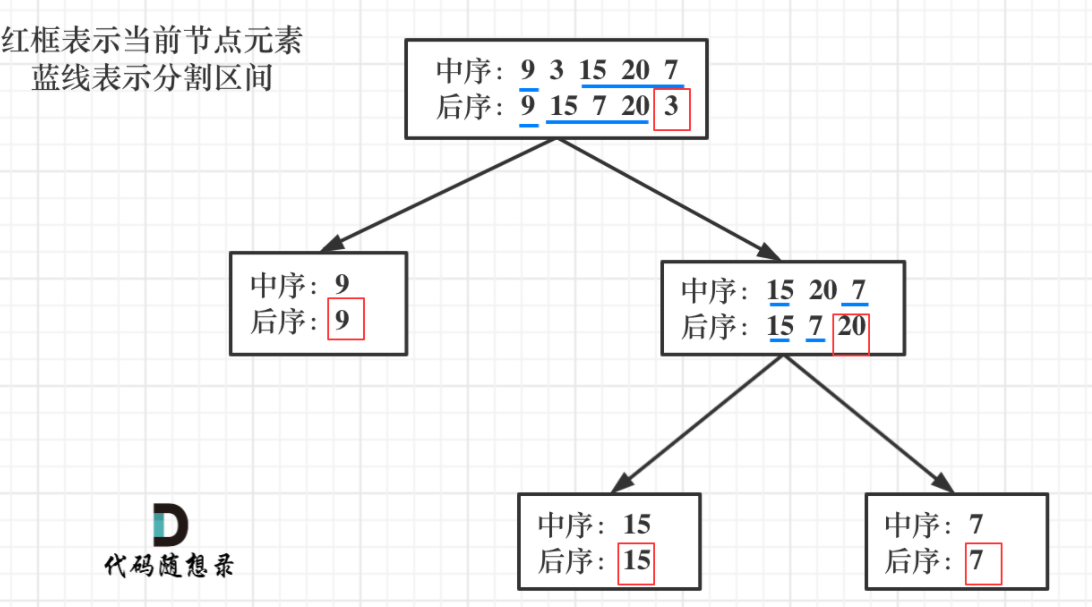
image.png

递归法

涉及到一层一层处理，肯定是要递归的，先捋一下思路，写个伪代码：

  1. TreeNode* traversal(indorder, postorder) {
  2.     if (postorder.empty()) return nullptr; // 序列为空，直接返回空节点
  4.     // 将后序遍历的最后一个元素取出，为根结点
  5.     int rootValue = postorder[size - 1];
  6.     TreeNode* root = new TreeNode(rootValue);
  8.     // 在inorder上找分割点，用于将其分为左右两部分
  9.     int index;
  10.     for (index = 0; index < inorder.size(); index++)
  11.         if (inorder[index] == rootValue) break;
  13.     // 切割中序数组 左闭右开 
  14.     // [0, index)
  15.     leftInorder = inorder(0, index);
  16.     // [index + 1, end)
  17.     rightInorder = inorder(index + 1, end);
  19.     // 切割后序数组 虽然元素位置不确定，但是后序子数组和中序子数组的长度是一样的
  20.     leftPostorder = inorder(0, index);
  21.     rightPostorder = inorder(index, end);
  23.     // 递归处理做数组和右数组
  24.     root->left = traversal(leftInorder, rightPostorder);
  25.     root->right = traversal(leftPostorder, rightInorder);
  27.     return root;
  28. }

完整代码：

  1. class Solution {
  2. public:
  3.     TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {
  4.         if (postorder.empty()) return nullptr;
  5.         // 取出根结点
  6.         int rootValue = *(postorder.end() - 1);
  7.         TreeNode* root = new TreeNode(rootValue);
  8.         // 寻找切割位置
  9.         int index = 0;
  10.         for(; index < inorder.size(); index++) {
  11.             if (inorder[index] == rootValue) break;
  12.         }
  13.         // 切割中序数组
  14.         vector<int> leftInorder(inorder.begin(), inorder.begin() + index);
  15.         vector<int> rightInorder(inorder.begin() + index + 1, inorder.end());
  16.         // 切割后序数组
  17.         vector<int> leftPostorder(postorder.begin(), postorder.begin() + index);
  18.         vector<int> rightPostorder(postorder.begin() + index, postorder.end() - 1);
  20.         //递归处理
  21.         root->left = buildTree(leftInorder, leftPostorder);
  22.         root->right = buildTree(rightInorder, rightPostorder);
  24.         return root;
  26.     }
  27. };

上面的代码每次都考重新构造vector，浪费时间和空间，可以改成用下标来递归，这样比较快

  1. class Solution {
  2. public:
  3.     TreeNode* traversal(vector<int>& inorder, int iBegin, int iEnd, vector<int>& postorder, int pBegin, int pEnd) {
  4.         if (pBegin == pEnd) return nullptr;
  5.         // 取出根结点
  6.         int rootValue = postorder[pEnd - 1];
  7.         TreeNode* root = new TreeNode(rootValue);
  9.         if (pEnd - pBegin == 1) return root;
  11.         // 寻找切割位置
  12.         int index = iBegin;
  13.         for(; index < iEnd; index++) {
  14.             if (inorder[index] == rootValue) break;
  15.         }
  17.         //递归处理
  18.         root->left = traversal(inorder, iBegin, index, postorder, pBegin, pBegin + index - iBegin);
  19.         root->right = traversal(inorder, index + 1, iEnd, postorder, pBegin + index - iBegin, pEnd - 1);
  21.         return root;
  22.     }
  25.     TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {
  26.         return traversal(inorder, 0, inorder.size(), postorder, 0, postorder.size());
  27.     }
  28. };

这个索引容易找错，草稿纸上多分析分析！！

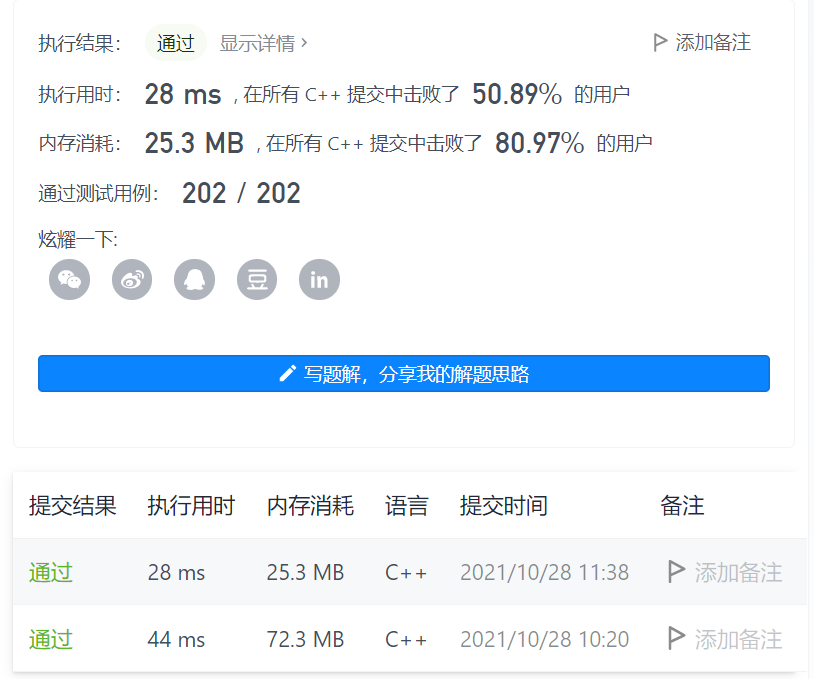image.png可以看到用索引进行递归，在时间和空间上都要省不少。

迭代法

先空着

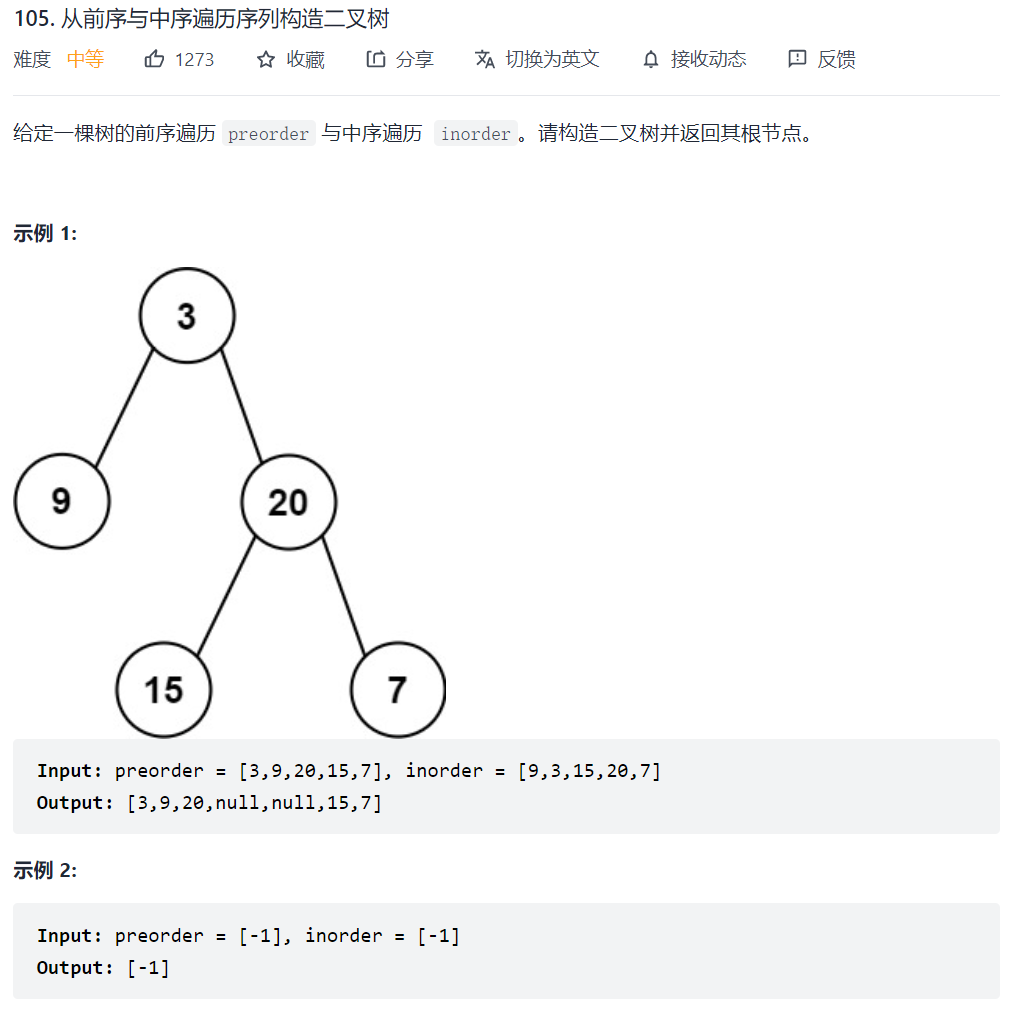
105. 从前序与中序遍历序列构造二叉树

image.png

递归法

这道题与上一道题一样，先序遍历的第一个元素一定是根结点，用它来将中序遍历分割为左右子树，然后递归划分，同样要注意索引的选取

class Solution {
public:
    TreeNode* build(vector<int>& preorder, int pBeg, int pEnd, vector<int>& inorder, int iBeg, int iEnd) {
        if (pBeg >= pEnd) {
            return nullptr;
        }
        TreeNode* root = new TreeNode(preorder[pBeg]);
        if (pBeg == pEnd - 1) {
            return root;
        }
        int index = iBeg;
        while (index < iEnd && inorder[index] != preorder[pBeg]) ++index;

        root->left = build(preorder, pBeg + 1, pBeg + index - iBeg + 1, inorder, iBeg, index);
        root->right = build(preorder, pBeg + index - iBeg + 1, pEnd, inorder, index + 1, iEnd);
        return root;
    }
    TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
        return build(preorder, 0, preorder.size(), inorder, 0, inorder.size());
    }
};

654. 最大二叉树

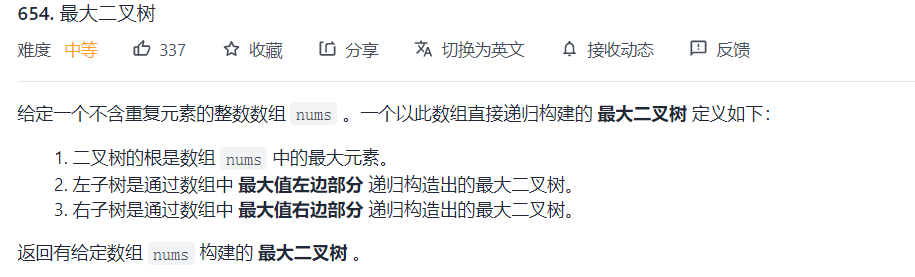
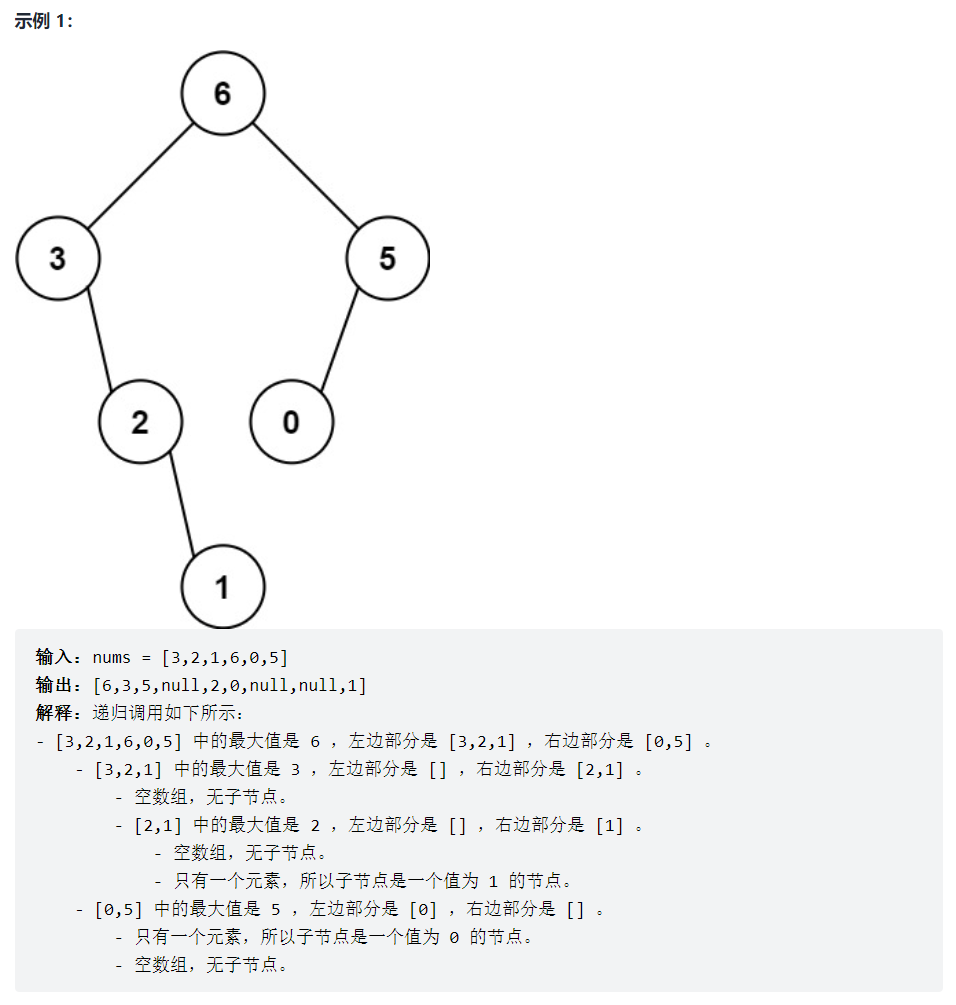
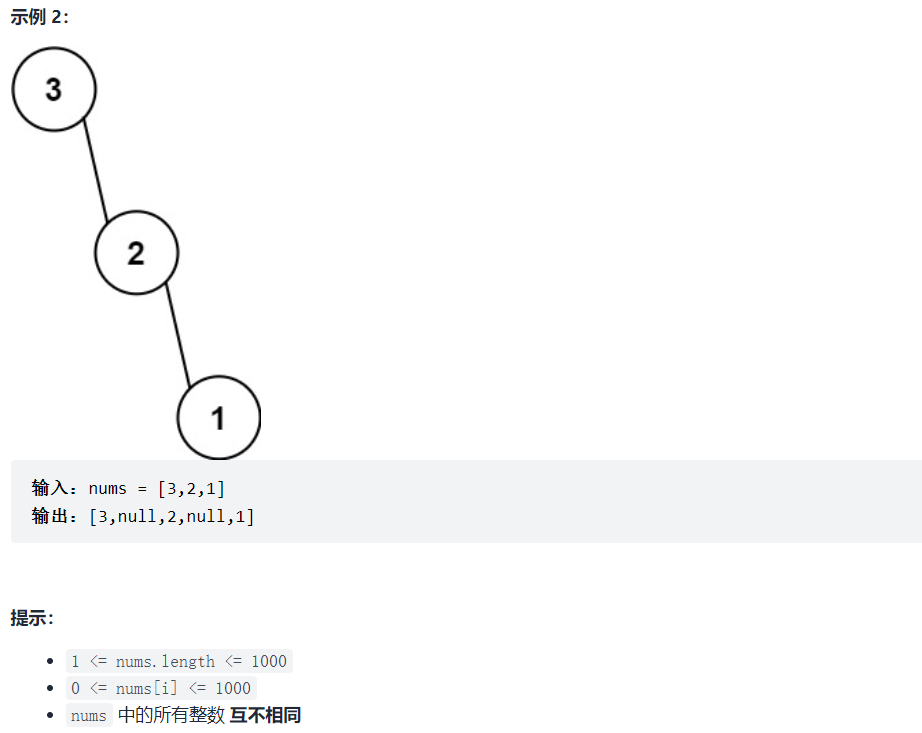
image.png
image.png
image.png

与从中序和后序（先序）遍历构造二叉树思路一样

  1. 递归的返回值和参数

构造一个数，所以肯定返回的是节点的指针
参数肯定要有数组nums，因为要根据最大值将数组划分为两部分，所以递归的参数要有起始下标

  1. 终止条件

坚持左闭右开原则，如果起始下标重叠，返回nullptr

  1. 单层递归的逻辑

寻找最大元素的位置，然后用最大元素构造根结点，划分数组，递归构造左右子树

class Solution {
public:
    TreeNode* traversal(vector<int>& nums, int begin, int end) {
        if (begin == end)
            return nullptr;
        int max_index = begin;
        for (int i = begin; i < end; i++) {
            if (nums[max_index] < nums[i])
                max_index = i;
        }
        TreeNode* root = new TreeNode(nums[max_index]);

        root->left = traversal(nums, begin, max_index);
        root->right = traversal(nums, max_index + 1, end);

        return root;

    }
    TreeNode* constructMaximumBinaryTree(vector<int>& nums) {
        return traversal(nums, 0, nums.size());
    }
};

image.png一次AC

617. 合并二叉树

image.png

递归法

  1. 递归的参数和返回值

返回树的节点，参数为两个节点

  1. 递归终止条件

如果两个节点都空，那么返回nullptr

  1. 单层递归逻辑
  • 有一个节点为空，那么返回不空的那个节点（这样就不用再递归了，因为返回的那个节点相当于返回了子树）
  • 两个节点都不空，构造新的节点，节点的值为两节点值之和
    • 递归构造左子树
    • 递归构造右子树

完整代码：（一遍AC）

class Solution {
public:
    TreeNode* mergeTrees(TreeNode* root1, TreeNode* root2) {
        if (!root1 && !root2) return nullptr;
        TreeNode* newRoot;
        if (!root1) 
            newRoot = root2;
        else if (!root2)
            newRoot = root1;
        else {
            newRoot = new TreeNode(root1->val + root2->val);
            newRoot->left = mergeTrees(root1->left, root2->left);
            newRoot->right = mergeTrees(root1->right, root2->right);
        }
        return newRoot;
    }
};

image.png
这个用的是前序遍历，中序和后序也是可以的，就是处理根结点的位置换一下
当然也可以不构造新的二叉树，直接把root1或者root2覆盖

迭代法

迭代法可以按照相同的树的做法，使用层序遍历来进行两根二叉树的合并

class Solution {
public:
    TreeNode* mergeTrees(TreeNode* root1, TreeNode* root2) {
        if (!root1) return root2;
        if (!root2) return root1;
        queue<TreeNode*> que;
        que.push(root1);
        que.push(root2);
        while (!que.empty()) {
            TreeNode* cur1 = que.front(); que.pop();
            TreeNode* cur2 = que.front(); que.pop();
            // 两节点一定都不为空
            cur1->val += cur2->val; 

            // cur1左节点cur2的左节点都不为空，加入队列
            if (cur1->left && cur2->left) {
                que.push(cur1->left);
                que.push(cur2->left);
            }
            // cur1右节点cur2的右节点都不为空，加入队列
            if (cur1->right && cur2->right) {
                que.push(cur1->right);
                que.push(cur2->right);
            }
            // 第一根树为最后返回的树，因此只考虑cur1子树为空的情况，进行赋值，赋值后就不用入队再处理了
            // cur1的左节点为空, cur2的左节点不为空
            if (!cur1->left && cur2->left)
                cur1->left = cur2->left;

            // cur1的右节点为空, cur2的左节点不为空
            if (!cur1->right && cur2->right)
                cur1->right = cur2->right;
        }
        return root1;
    }
};

image.png
好像还不如递归好用，重在理解思路