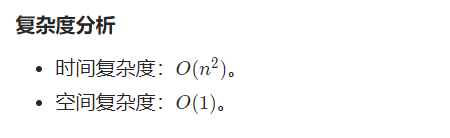- 300. 最长递增子序列">300. 最长递增子序列
- 674. 最长连续递增序列">674. 最长连续递增序列
- 718. 最长重复子数组">718. 最长重复子数组
- 1143. 最长公共子序列">1143. 最长公共子序列
- 1035. 不相交的线">1035. 不相交的线
- 53. 最大子序和">53. 最大子序和
- 392. 判断子序列">392. 判断子序列
- 115. 不同的子序列">115. 不同的子序列
- 583. 两个字符串的删除操作">583. 两个字符串的删除操作
- 72. 编辑距离(全文背诵😊)">72. 编辑距离(全文背诵😊)
- 647. 回文子串">647. 回文子串
- 5. 最长回文子串">5. 最长回文子串
- 516. 最长回文子序列">516. 最长回文子序列
- 10. 正则表达式匹配💦">10. 正则表达式匹配💦
- 32. 最长有效括号">32. 最长有效括号
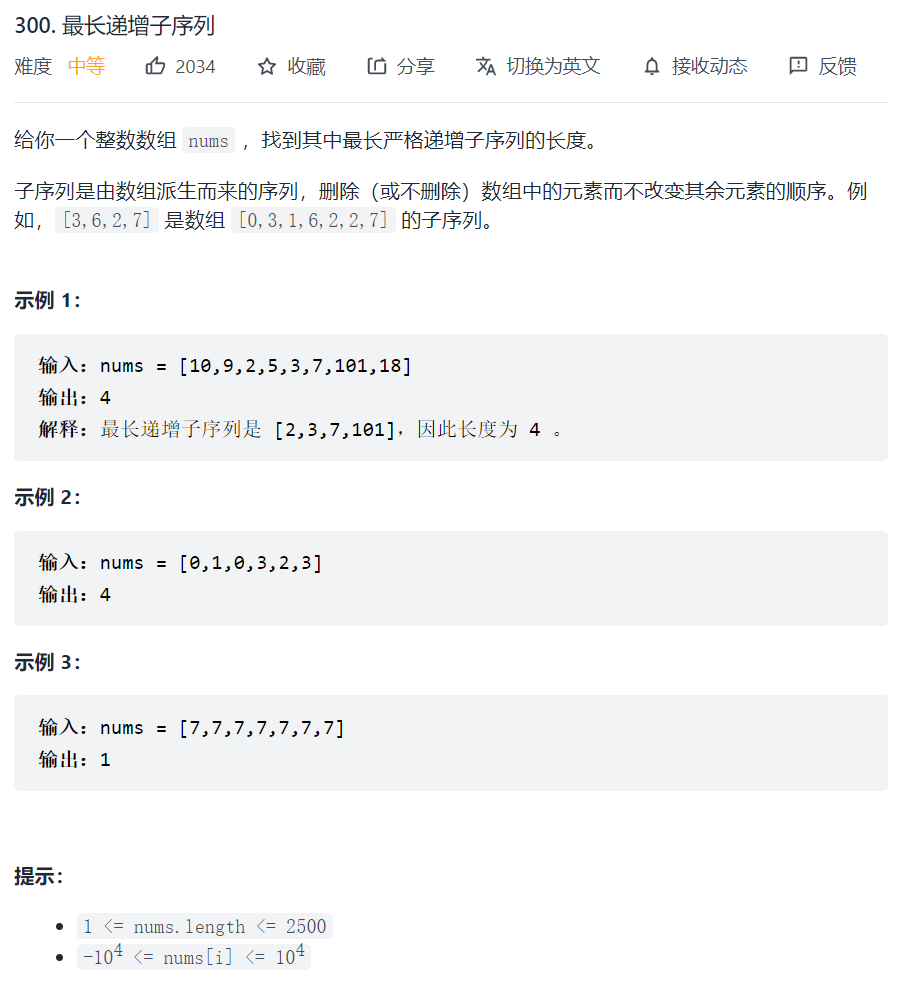
300. 最长递增子序列
思路1:动态规划
用一个dp数组,dp[i]代表以nums[i]为结尾的最大递增子序列长度,两个循环,外面循环遍历Nums,i从 0 - n-1,内部循环j由 0 - i , 每当nums[i] > nums[j] 的时候,就要判断是否更新dp数组
dp[i] = max(dp[i], dp[j] + 1)
最大的递增子序列的长度就是max(dp[i])
这种解法遍历所有情况,时间复杂度为O(n^2)
class Solution {public:int lengthOfLIS(vector<int>& nums) {int n = nums.size();if (n <= 1) return n;vector<int> dp(n, 1); // 初始长度为1,就是nums[i]自身int maxLen = 1;for (int i = 0; i < n; i++) { // 循环判断以nums[i]为结尾的最长递增子序列长度for (int j = 0; j < i; j++) {if (nums[j] < nums[i]) dp[i] = max(dp[i], dp[j] + 1); //每当nums[i]比nums[j]大的时候,都要判断是否更新}maxLen = max(maxLen, dp[i]);}return maxLen;}};
思路2:贪心+动态规划
这种方法可以找到最长递增子序列之一
用贪心 + 二分查找来将时间复杂度降为O(nlogn)
我们定义一个 dp 数组,其中 dp[k]表示长度为 k+1 的最长递增子序列的最后一个数字。
遍历每一个位置 i:
- 如果其对应的数字大于 dp 数组中所有数字的值,那么我们把它放在 dp 数组尾部,表示最长递增子序列长度加 1;
- 如果我们发现这个数字在 dp 数组中比数字 a 大、比数字 b 小,则我们将 b 更新为此数字,使得之后构成递增序列的可能性增大。(贪心策略:用小的替换大的,访问下一个元素时能够将其添加到递增子序列的可能性更大)
引用一个题解下评论区老哥的例子:
比如序列是78912345,前三个遍历完以后tail是789,这时候遍历到1,就得把1放到合适的位置,于是在tail二分查找1的位置,变成了189(如果序列在此时结束,因为res不变,所以依旧输出3),再遍历到2成为129,然后是123直到12345
如果例子中每次替换的都是dp数组的最后一个元素,那么就很难理解。其实当我们用一个较小的元素去替换dp中的任意一个元素时,由于替换后,数组的长度并不会发生改变,数组中的元素也不一定是要返回的那个最长上升子序列。但是正是因为替换不会改变数组长度,我们可以通过替换,让遍历数组后面的元素时,形成更长的上升子序列的可能更大,这就是贪心的策略。
最后最大递增子序列的长度应该是dp数组的长度
例子:
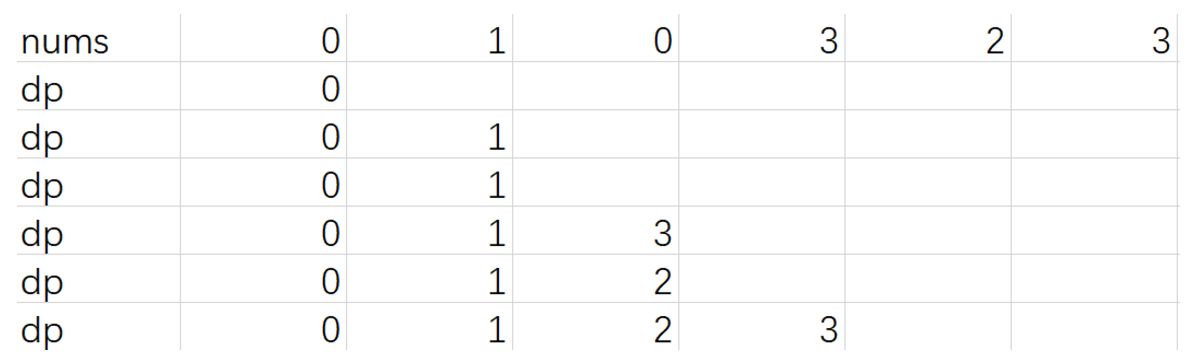
以这种方式维护的 dp 数组永远是递增的,因此可以用二分查找加速搜索。
1:二分查找使用STL lower_bound(dp.begin(), dp.end(), x);
class Solution {
public:
int lengthOfLIS(vector<int>& nums) {
int n = nums.size();
if (n <= 1) return n;
vector<int> dp; // 维护这个单调递增子序列 其实不应该叫dp了
// dp.push_back(nums[0]);
for (auto num : nums) {
if (dp.empty() || dp.back() < num) {
dp.push_back(num);
} else {
auto it = lower_bound(dp.begin(), dp.end(), num);
*it = num;
}
}
return dp.size();
}
};
2.手撸二分查找
class Solution {
public:
int lengthOfLIS(vector<int>& nums) {
int n = nums.size();
if (n <= 1) return n;
vector<int> dp;
dp.push_back(nums[0]);
for (int i = 1; i < n; i++) {
if (dp.back() < nums[i]) dp.push_back(nums[i]);
else { // 使用二分查找找第一个比nums[i]大的元素,并将其替换为nums[i]
int l = 0, r = dp.size() - 1;
while (l <= r) {
int mid = l + r >> 1;
if (dp[mid] < nums[i]) {
l = mid + 1;
} else {
r = mid - 1;
}
}
dp[l] = nums[i]; // 已经排除了所有元素都比nums[i]小的情况
}
}
return dp.size();
}
};
674. 最长连续递增序列

这道题和 300.最长自增子序列 不同,要子序列连续,连续子序列就是数组
思路一:动态规划
因为要求子序列连续,所以状态转移方程有所不同,当nums[i] > nums[i - 1]时,dp[i] = dp[i - 1] + 1,在刚才的基础上,长度加一,否则什么都不做
class Solution {
public:
int findLengthOfLCIS(vector<int>& nums) {
int n = nums.size();
if (n <= 1) return n;
vector<int> dp(n, 1);
int res = 0;
for (int i = 1; i < n; i++) {
if (nums[i] > nums[i - 1]) dp[i] = dp[i - 1] + 1;
res = max(res, dp[i]);
}
return res;
}
};
空间复杂度优化:
class Solution {
public:
int findLengthOfLCIS(vector<int>& nums) {
int n = nums.size();
if (n <= 1) return n;
vector<int> dp(n, 1);
int res = 0, a = 1;
for (int i = 1; i < n; i++) {
if (nums[i] > nums[i - 1]) a += 1;
else a = 1;
res = max(res, a);
}
return res;
}
};
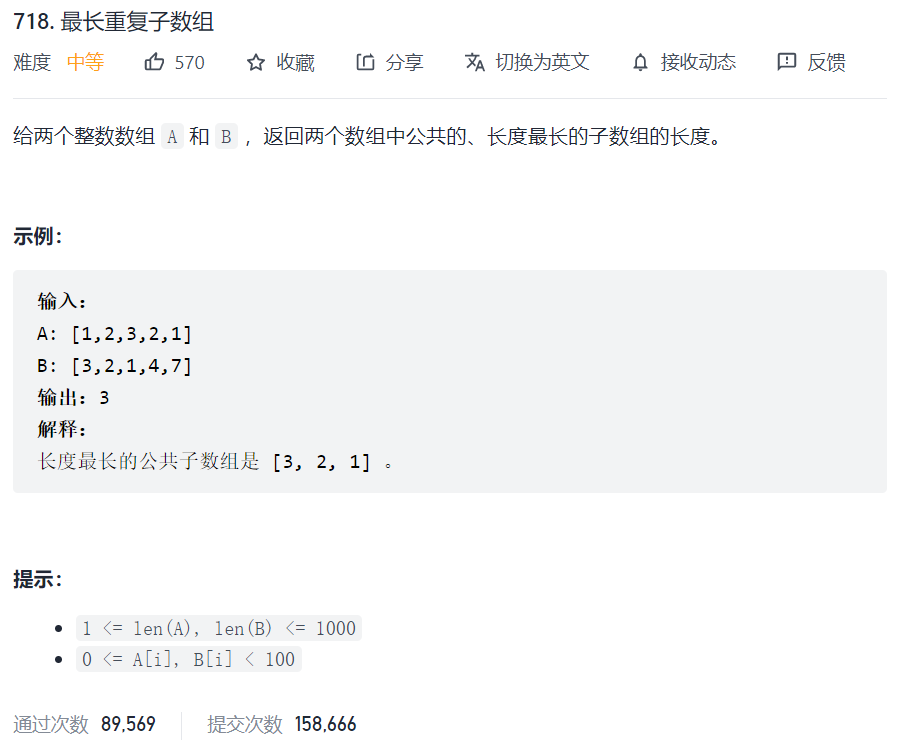
718. 最长重复子数组
思路一:动态规划
与最长公共子序列类似,还是要区分一点力扣的题目,子数组是连续的,而子序列可以不连续,因此最长公共子序列要比这道题难一些。
首先明确一点,最长重复子数组就是最长连续且相等的子数组
二维dp[i][j]表示 字符串A以 i - 1 结尾,字符串B以 j - 1 结尾的最长连续子数组的长度,
如果 nums1[i - 1] = nums2[j - 1]的话,dp[i][j] = dp[i - 1][j - 1] + 1
class Solution {
public:
int findLength(vector<int>& nums1, vector<int>& nums2) {
int m = nums1.size(), n = nums2.size();
vector<vector<int>> dp(m + 1, vector<int>(n + 1, 0));
int res = 0;
for (int i = 1; i <= m; i++) {
for (int j = 1; j <= n; j++) {
if (nums1[i - 1] == nums2[j - 1]) { // 如果两个数字相等的话,在之前最长子数组的基础上 + 1
dp[i][j] = dp[i - 1][j - 1] + 1;
}
res = max(res, dp[i][j]); // res 更新为最长的结果
}
}
return res;
}
};
- 时间复杂度O(n * m) n 为A长度,m为B长度
- 空间复杂度O(n * m)
滚动数组优化
dp[i][j]由dp[i - 1][j - 1]推来,因此可以将dp数组压缩为一维,类似于背包问题,为了使用上一层的元素,需要从后向前遍历
class Solution {
public:
int findLength(vector<int>& nums1, vector<int>& nums2) {
int m = nums1.size(), n = nums2.size();
vector<int> dp(n + 1, 0);
int res = 0;
for (int i = 1; i <= m; i++) {
for (int j = n; j > 0; j--) {
if (nums1[i - 1] == nums2[j - 1]) { // 如果两个数字相等的话,在之前最长子数组的基础上 + 1
dp[j] = dp[j - 1] + 1;
} else {
dp[j] = 0; // 不相等要更新为0
}
res = max(res, dp[j]); // res 更新为最长的结果
}
}
return res;
}
};
- 时间复杂度O(n * m) n 为A长度,m为B长度
- 空间复杂度O(m)
思路二:滑动窗口💦
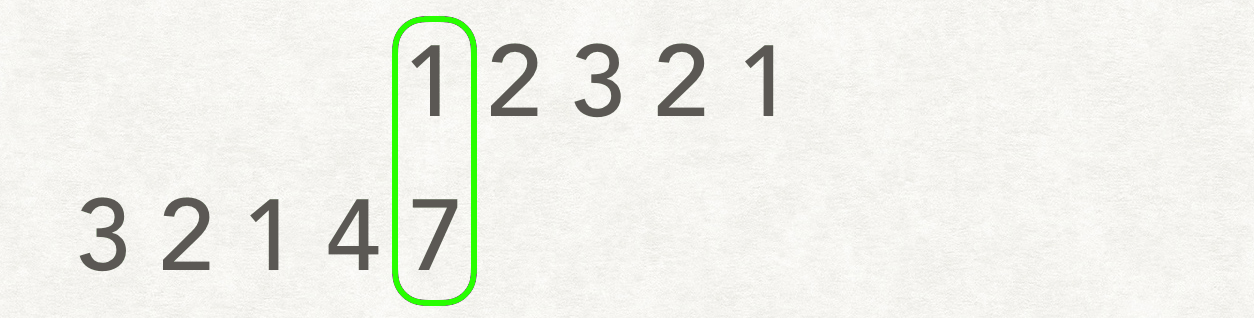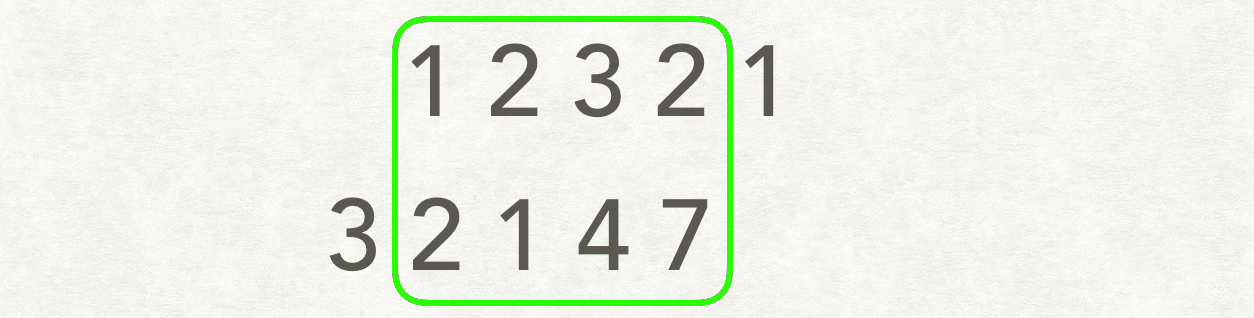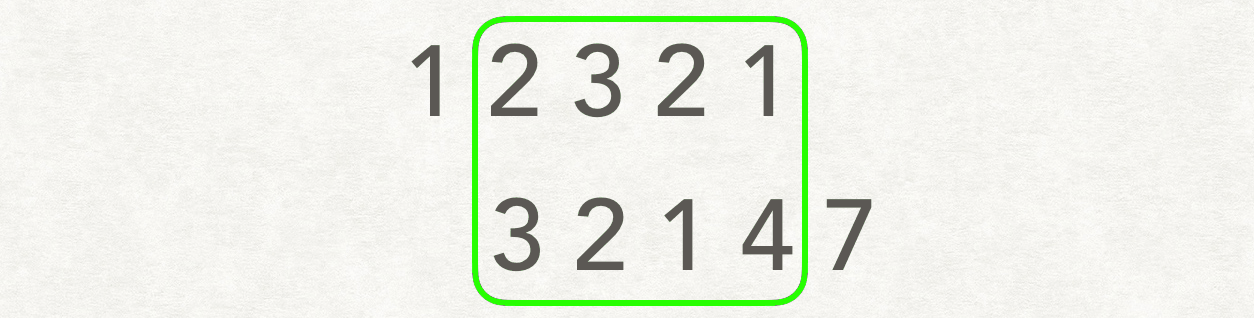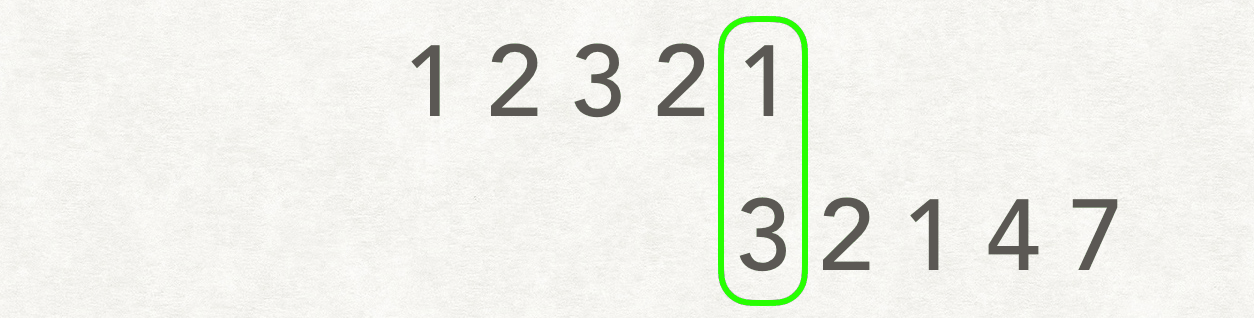
将两个数组不同位置对齐,然后比较这个“窗口”内最长的重复子数组
class Solution {
public:
int maxLen(vector<int>& nums1, vector<int>& nums2, int a, int b, int len) { // 将索引a,b对齐
int res = 0, k = 0;
for (int i = 0; i < len; i++) {
if (nums1[i + a] == nums2[i + b]) k++;
else k = 0;
res = max(k, res);
}
return res;
}
int findLength(vector<int>& nums1, vector<int>& nums2) {
int m = nums1.size(), n = nums2.size();
int res = 0, maxL = 0;
for (int i = 0; i < m; i++) {
int len = min(n, m - i); // 窗口的长度
maxL = maxLen(nums1, nums2, i, 0, len);
res = max(res, maxL);
}
for (int i = 0; i < n; i++) {
int len = min(m, n - i);
maxL = maxLen(nums1, nums2, 0, i, len);
res = max(res, maxL);
}
return res;
}
};
- 时间复杂度 O(M + N) * min(M, N)
1143. 最长公共子序列

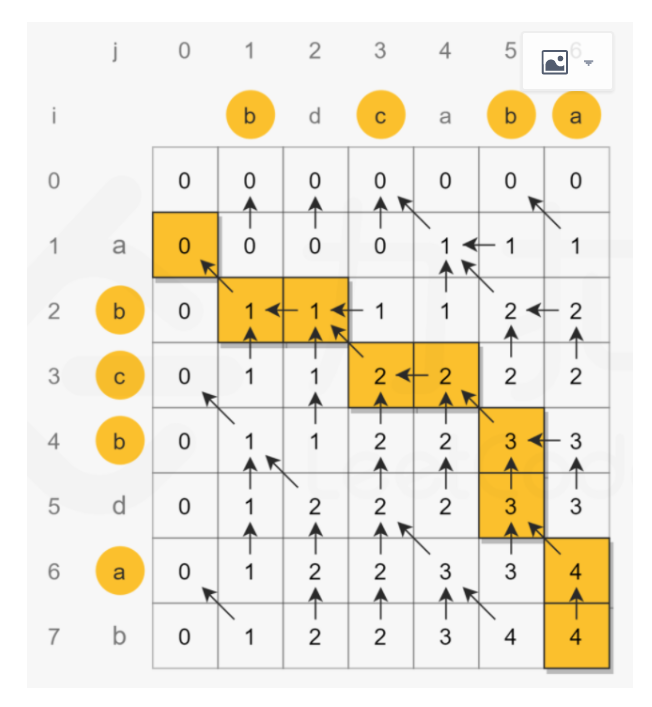
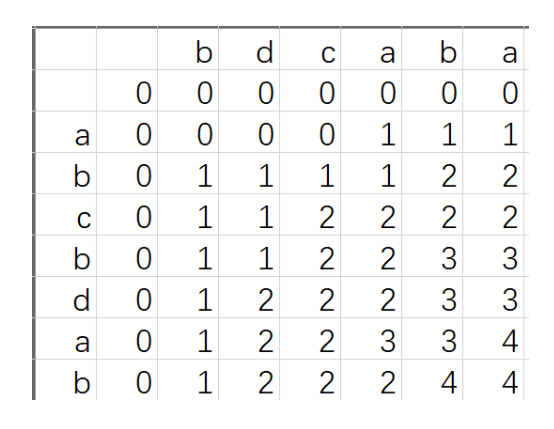
假设字符串 text1和 text2 的长度分别为m和n, 创建 m+1 行 n+1 列的二维数组 dp,其中 dp[i][j] 表示 text1[0 : i) 和 text2[0 : j)的最长公共子序列的长度
其中:text1[0 : i]表示text1长度为i的前缀,text2[0 : j]表示text2长度为j的前缀
如果text1[i] 和 text[j] 相等的话 ,那么必然最大公共子序列的长度为 dp[i-1][j-1] + 1
如果text1[i] 和 text[j] 不相等的话,最大公共子序列的长度应该取 dp[i-1][j] 和 dp[i][j-1]的最大值
class Solution {
public:
int longestCommonSubsequence(string text1, string text2) {
int m = text1.size(), n = text2.size();
vector<vector<int>> dp(m + 1, vector<int>(n + 1, 0));
for (int i = 1; i <= m; i++) {
for (int j = 1; j <= n; j++) {
if (text1[i - 1] == text2[j - 1]) {
dp[i][j] = dp[i - 1][j - 1] + 1;
} else {
dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);
}
}
}
return dp[m][n];
}
};
1035. 不相交的线

不相交的线实际上就是求两个数组的最长公共子序列,两个相同的数字可以连一根线,只要保证不改变数字的相对位置,那么线就不会相交。
所以这一题与1143题代码一样
class Solution {
public:
int maxUncrossedLines(vector<int>& nums1, vector<int>& nums2) {
int m = nums1.size(), n = nums2.size();
vector<vector<int>> dp(m + 1, vector<int>(n + 1, 0));
for (int i = 1; i <= m; i++) {
for (int j = 1; j <= n; j++) {
if (nums1[i - 1] == nums2[j - 1]) {
dp[i][j] = dp[i - 1][j - 1] + 1;
} else {
dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);
}
}
}
return dp[m][n];
}
};
53. 最大子序和


假设nums数组的长度为n,下标范围为0 ~ n-1
可以设f(i)为以nums[i]为结尾的最大子序和,用dp数组来存储f(i)的值,那么最后的结果应该是dp数组的最大值,dp[i]的状态转移方程为
class Solution {
public:
int maxSubArray(vector<int>& nums) {
int n = nums.size();
vector<int> dp(n);
dp[0] = nums[0];
int res = dp[0];
for (int i = 1; i < n; i++) {
dp[i] = max(dp[i - 1] + nums[i], nums[i]);
res = max(res, dp[i]);
}
return res;
}
};
将空间复杂度由O(n)减小为O(1)
class Solution {
public:
int maxSubArray(vector<int>& nums) {
int n = nums.size();
if (n == 1) return nums[0]; // nums.length >= 1
int res = nums[0];
int pre = 0;
for (int i = 0; i < n; ++i) {
pre = max(nums[i], pre + nums[i]);
res = max(res, pre);
}
return res;
}
};
或者
class Solution {
public:
int maxSubArray(vector<int>& nums) {
int pre = 0, res = nums[0];
for (const auto & num : nums) {
pre = max(num, pre + num);
res = max(res, pre);
}
return res;
}
};

392. 判断子序列

双指针
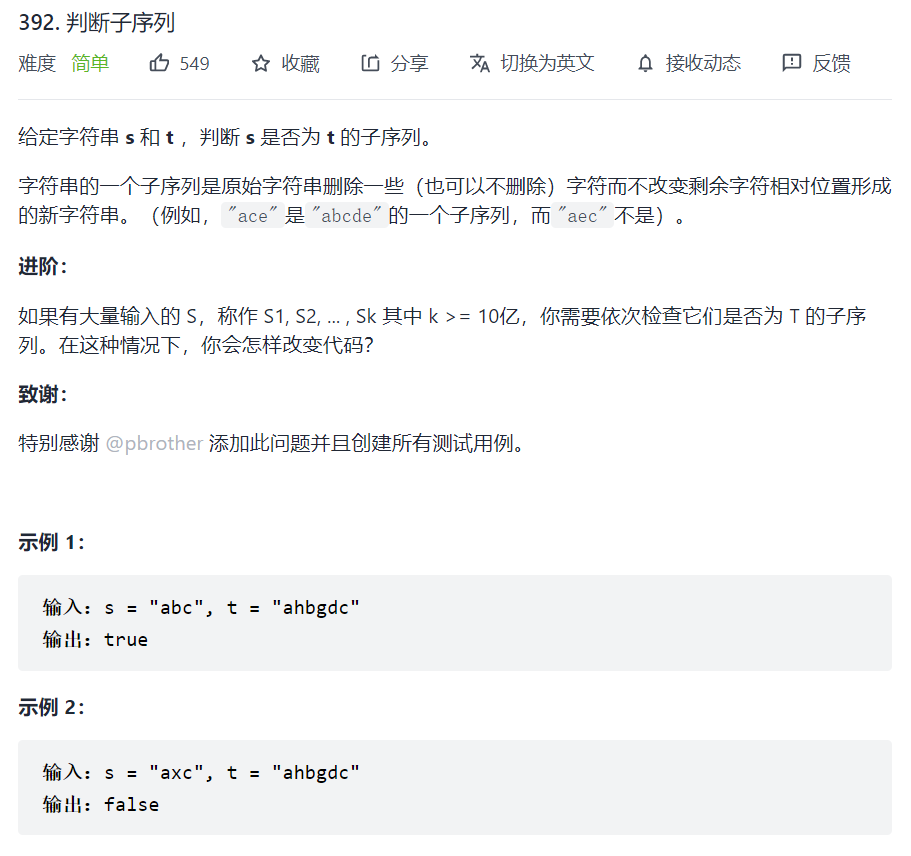
用两个指针分别指向主串和模式串,从左向右逐个进行匹配,如果两个字符相等,那么指针同时右移,否则主串的指针右移,如果最后匹配成功则返回true
class Solution {
public:
bool isSubsequence(string s, string t) {
if (s.empty()) return true;
int j = 0;
for (int i = 0; i < t.size(); i++) {
if (t[i] == s[j]) {
j++;
}
}
return j == s.size();
}
};
- 时间复杂度 O(n)
-
动态规划:编辑距离
记dp[i][j] 表示以下标 i-1 为结尾的字符串s和以下标 j-1为结尾的字符串t,相同子序列的长度
在确定递推公式的时候,首先要考虑如下两种操作,整理如下: if (s[i - 1] == t[j - 1])
- t中找到了一个字符在s中也出现了
- if (s[i - 1] != t[j - 1])
- 相当于t要删除元素,继续匹配
if (s[i - 1] == t[j - 1]),那么dp[i][j] = dp[i - 1][j - 1] + 1;,因为找到了一个相同的字符,相同子序列长度自然要在dp[i-1][j-1]的基础上加1
if (s[i - 1] != t[j - 1]),此时相当于t要删除元素,t如果把当前元素t[j - 1]删除,那么dp[i][j] 的数值就是 看s[i - 1]与 t[j - 2]的比较结果了,即:dp[i][j] = dp[i][j - 1];
都初始化为0,遍历顺序从上到下,从左到右。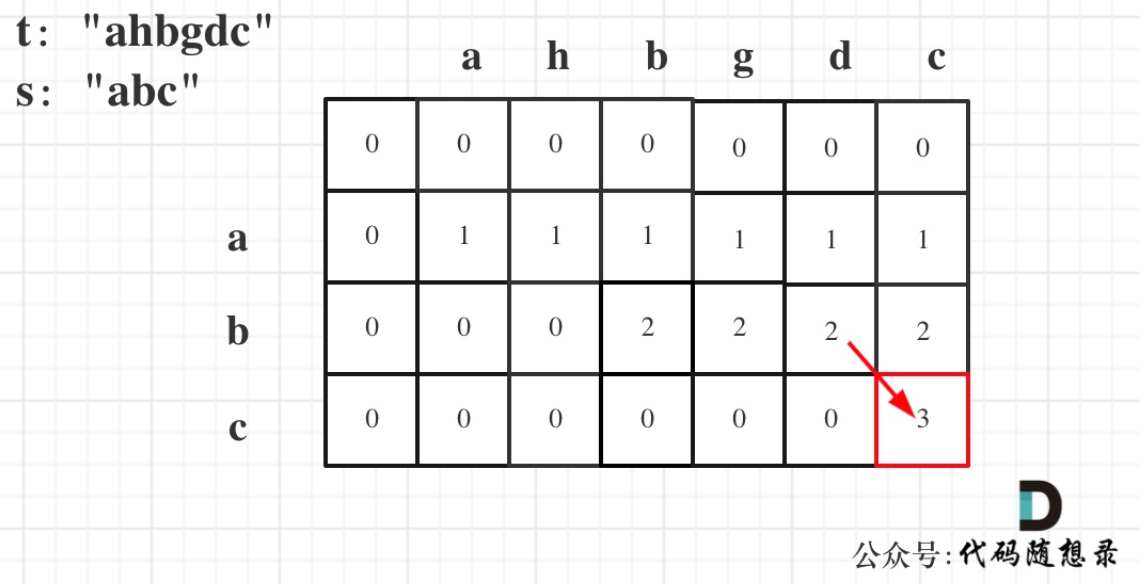
class Solution {
public:
bool isSubsequence(string s, string t) {
vector<vector<int>> dp(s.size() + 1, vector<int>(t.size() + 1, 0));
for (int i = 1; i <= s.size(); i++) {
for (int j = 1; j <= t.size(); j++) {
if (s[i - 1] == t[j - 1]) dp[i][j] = dp[i - 1][j - 1] + 1;
else dp[i][j] = dp[i][j - 1];
}
}
if (dp[s.size()][t.size()] == s.size()) return true;
return false;
}
};
- 时间复杂度O(m * n)
- 空间复杂度O(m * n)
115. 不同的子序列
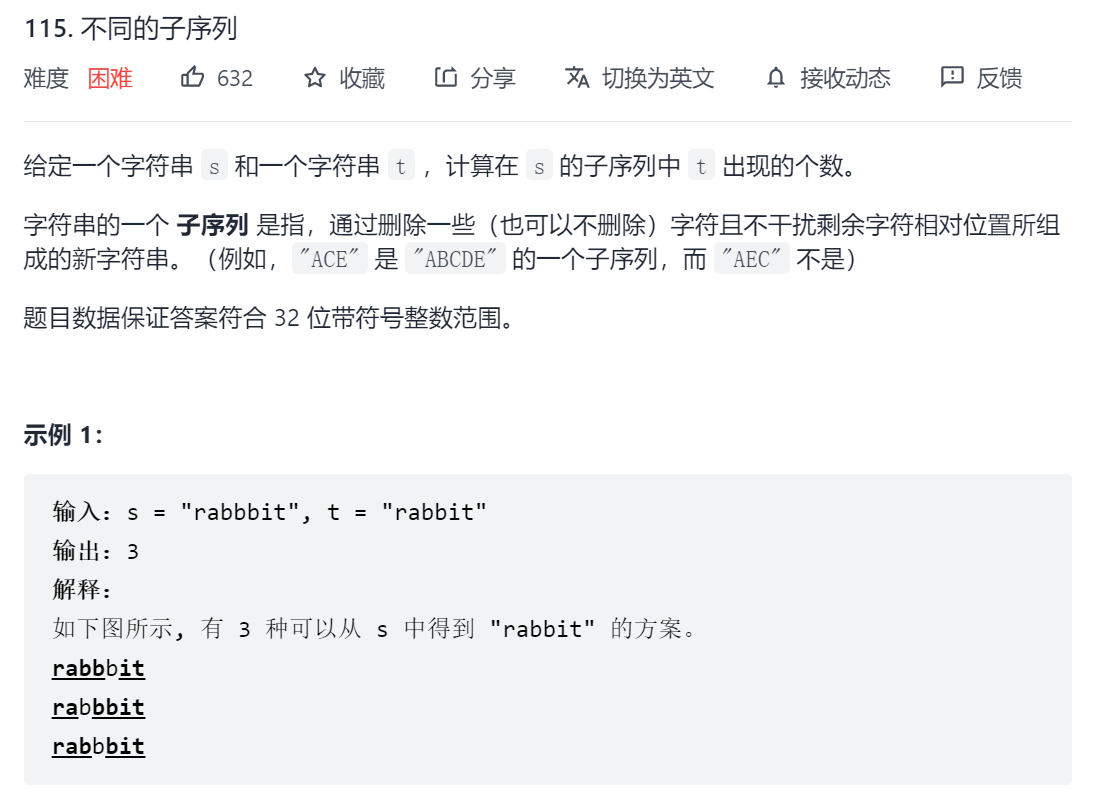

定义dp[i][j]表示以s[i-1]为结尾的s的子序列中,出现了多少次t[j -1]为结尾的t的子串,
假设s[i] = t[i],如果以t[i - 1]为结尾的序列记为a, 在s[i - 1]为结尾的字符串b中出现了x次,那么以s[i]为结尾的字符串中出现序列a的次数应该加上x,也有可能在b中就存在y个a,那么有:
s[i-1] = t[i-1]:
- 使用s[i-1]来构成子序列,有dp[i-1][j-1]种情况
- 不使用s[i-1]来构成子序列,有dp[i-1][j]种情况
- 综上这种情况下 dp[i][j] = dp[i-1][j-1] + dp[i-1][j]
s[i-1] != t[i-1]: 只能是dp[i][j] = dp[i-1][j],当前访问的两个字符不相同,所以只能用之前的结果
初始化:j = 0 时,从t中取的子序列是个空串,从s中不取任何字符就可以,那么dp[i][0] = 1。其他的就赋值为0就好了
正向遍历!
C++代码:
class Solution {
public:
int numDistinct(string s, string t) {
int m = s.size(), n = t.size();
// 测试用例比较恶心,用长整型
vector<vector<uint64_t>> dp(m + 1, vector<uint64_t>(n + 1, 0));
for (int i = 0; i <= m; i++) dp[i][0] = 1; // 初始化
for (int i = 1; i <= m; i++) {
for (int j = 1; j <= n; j++) {
if (s[i - 1] == t[j - 1]) {
// 当前字符相等的,出现子序列的情况有两种可能, 用或者不用s[i-1]
dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j];
} else {
dp[i][j] = dp[i - 1][j];
}
}
}
return dp[m][n];
}
};
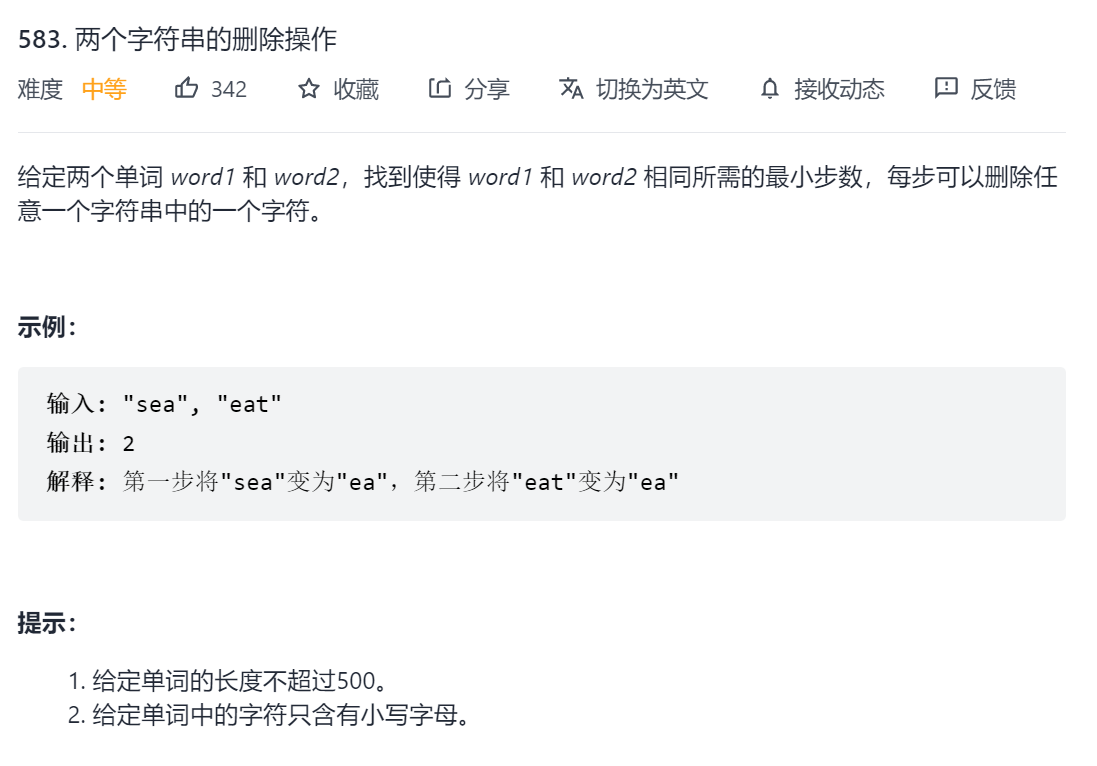
583. 两个字符串的删除操作
思路一:求最大公共子序列LCS
最小的删除步骤使得两字符串相等,每次删除一个字符,要想让操作更少,那必然是剩下的越多操作越少,剩下的最多,并且还要相同,那剩下的就是两字符串的最长公共子序列了。
class Solution {
public:
int minDistance(string word1, string word2) {
int m = word1.size(), n = word2.size();
vector<vector<int>> dp(m + 1, vector<int>(n + 1, 0));
for (int i = 1; i <= m; i++) {
for (int j = 1; j<= n; j++) {
if (word1[i - 1] == word2[j - 1]) {
dp[i][j] = dp[i - 1][j - 1] + 1;
} else {
dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);
}
}
}
return m + n - 2 * dp[m][n];
}
};
思路二:直接考虑删除的dp
dp[i][j]:以i-1为结尾的字符串word1,和以j-1位结尾的字符串word2,想要达到相等,所需要删除元素的最少次数。
同样需要判断当前访问的两个字符是否相等:
当word1[i - 1] 与 word2[j - 1]相同的时候,dp[i][j] = dp[i - 1][j - 1];
当word1[i - 1] 与 word2[j - 1]不相同的时候,有两种情况:
- 删word1[i - 1],最少操作次数为dp[i - 1][j] + 1
- 删word2[j - 1],最少操作次数为dp[i][j - 1] + 1
最后取最小值,所以当word1[i - 1] 与 word2[j - 1]不相同的时候,递推公式:dp[i][j] = min(dp[i - 1][j] + 1, dp[i][j - 1] + 1);
需要初始化,假如i = 0,表示word1一个字符都不取,要想让word1和word2相等,必须把word2中的都删了才行,j=0同理,因此应该这样初始化:
for (int i = 1; i <= word1.size(); i++) dp[i][0] = i;
for (int j = 1; j <= word2.size(); j++) dp[0][j] = j;
class Solution {
public:
int minDistance(string word1, string word2) {
int m = word1.size(), n = word2.size();
vector<vector<int>> dp(m + 1, vector<int>(n + 1, 0));
for (int i = 1; i <= m; i++) dp[i][0] = i; // 初始化
for (int j = 1; j <= n; j++) dp[0][j] = j; // 初始化
for (int i = 1; i <= m; i++) {
for (int j = 1; j <= n; j++) {
if (word1[i - 1] == word2[j - 1]) {
// 当前字符相等的,不用操作
dp[i][j] = dp[i - 1][j - 1];
} else { // 字符不相等时,考虑删除哪一个会使步数最少
dp[i][j] = min(dp[i - 1][j] + 1, dp[i][j - 1] + 1);
}
}
}
return dp[m][n];
}
};
};
72. 编辑距离(全文背诵😊)
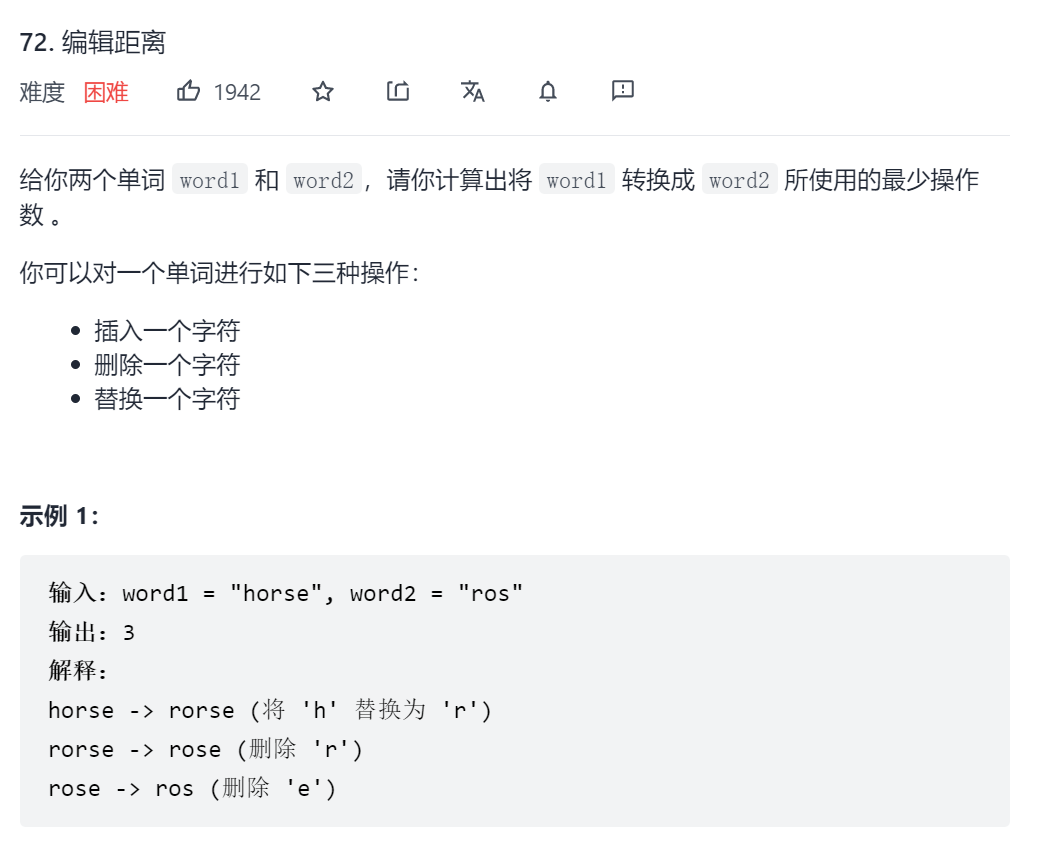

记dp[i][j] 表示以下标i-1为结尾的字符串word1,和以下标j-1为结尾的字符串word2,最近编辑距离为dp[i][j]。
代码框架为:
if(word[i - 1] == word[j - 1])
不操作
else
增删改
确定递推公式:
- 如果word[i - 1] = word[j - 1]的话,不操作,那么dp[i][j] = dp[i - 1][j - 1]
- 如果word[i - 1] != word[j - 1]的话:
- word1中删除word1[i - 1] : dp[i][j] = dp[i - 1][j] + 1
- word2中删除word2[i - 1] : dp[i][j] = dp[i][j - 1] + 1
- 替换word1或者word2中的一个字母 : dp[i][j] = dp[i - 1][j - 1] + 1
注:添加操作可以视为删除操作
word2添加一个元素,相当于word1删除一个元素,例如 word1 = “ad” ,word2 = “a”,word1删除元素’d’ 和 word2添加一个元素’d’,变成word1=”a”, word2=”ad”, 最终的操作数是一样!
初始化操作与两个字符串的删除操作类似,将一个字符串和一个空串变成相同的字符串需要操作的次数为字符串的长度
class Solution {
public:
int minDistance(string word1, string word2) {
int m = word1.size(), n = word2.size();
vector<vector<int>> dp(m + 1, vector<int>(n + 1, 0));
// 初始化
for (int i = 1; i <= m; i++) dp[i][0] = i;
for (int i = 1; i <= n; i++) dp[0][i] = i;
for (int i = 1; i <= m; i++) {
for (int j = 1; j <= n; j++) {
if (word1[i - 1] == word2[j - 1]) {// 相等不用操作
dp[i][j] = dp[i - 1][j - 1];
} else {
dp[i][j] = min({dp[i - 1][j], dp[i][j - 1], dp[i - 1][j - 1]}) + 1;
}
}
}
return dp[m][n];
}
};
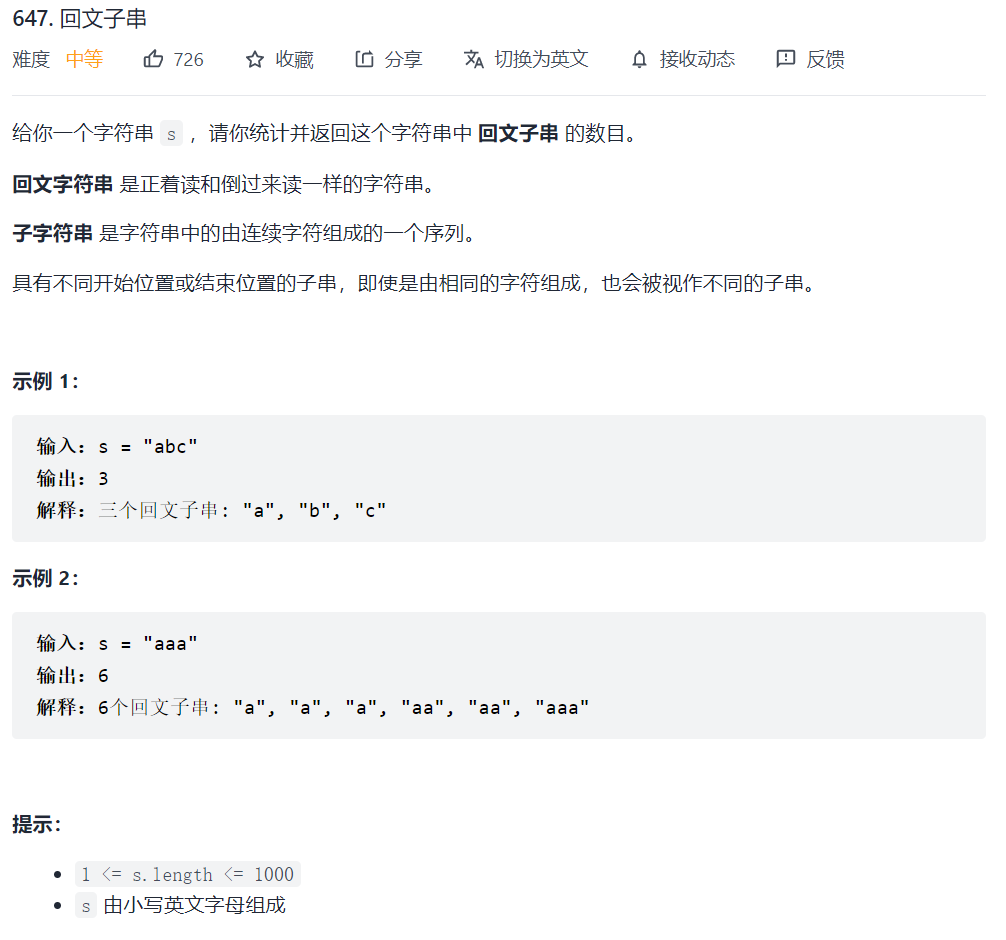
647. 回文子串
动态规划
布尔类型的dp[i][j]:表示区间范围[i,j] (注意是左闭右闭)的子串是否是回文子串,如果是dp[i][j]为true,否则为false。
在确定递推公式时,就要分析如下几种情况。
整体上是两种,就是s[i]与s[j]相等,s[i]与s[j]不相等这两种。
当s[i]与s[j]不相等,dp[i][j]一定是false。
当s[i]与s[j]相等时,有如下三种情况
- 情况一:下标i 与 j相同,同一个字符例如a,当然是回文子串
- 情况二:下标i 与 j相差为1,例如aa,也是文子串
- 情况三:下标:i 与 j相差大于1的时候,例如cabac,此时s[i]与s[j]已经相同了,我们看i到j区间是不是回文子串就看aba是不是回文就可以了,那么aba的区间就是 i+1 与 j-1区间,这个区间是不是回文就看dp[i + 1][j - 1]是否为true。
递推公式如下:
if (s[i] == s[j]) {
if (j - i <= 1 || dp[i + 1][j - 1] == true) {
dp[i][j] = true;
}
}
从情况三可以看出,dp推导的时候需要下一行和前一列数据,所以要先算下面的行,左边的列。为了保证每次递推的时候,dp[i + 1][j - 1]已经经过计算,遍历顺序必须为从下到上,从左到右。
class Solution {
public:
int countSubstrings(string s) {
int n = s.size();
int res = 0;
vector<vector<bool>> dp(n, vector<bool>(n, false));
for (int i = n - 1; i >= 0; i--) {// 从下到上
for (int j = i; j < n; j++) { // 从左到右
if (s[i] == s[j] && (j - i <= 1 || dp[i + 1][j - 1])) {
res++;
dp[i][j] = true;
}
}
}
return res;
}
};
动态规划是空间复杂度比较高
中心扩展
在实现的时候,我们需要处理一个问题,即如何有序地枚举所有可能的回文中心,我们需要考虑回文长度是奇数和回文长度是偶数的两种情况。如果回文长度是奇数,那么回文中心是一个字符;如果回文长度是偶数,那么中心是两个字符。当然你可78以做两次循环来分别枚举奇数长度和偶数长度的回文,但是我们也可以用一个循环搞定。我们不妨写一组出来观察观察,假设 n = 4,我们可以把可能的回文中心列出来: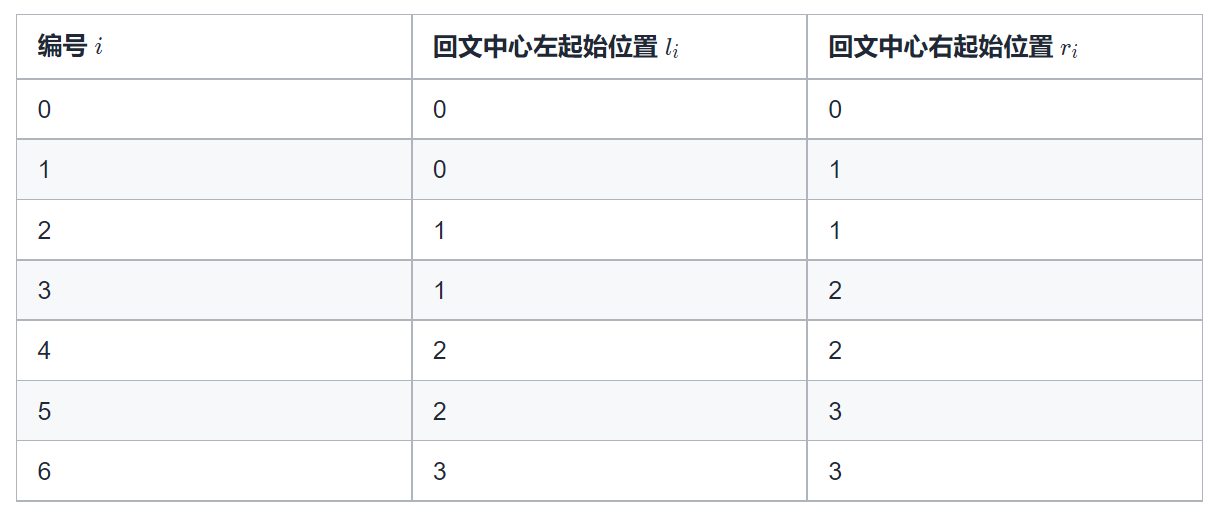
回文长度是奇数的回文中心有 0 ~ 3共 4个, 回文长度是偶数的回文中心,有(0,1)(1,2)(2,3)共4 - 1对,推广到一般情况,长度为n的字符串会生成 组回文中心
。其中
。这样只要从0到
遍历i,就可以得到所有可能的回文中心,这样就把技术长度和偶数长度两种情况统一起来了。
class Solution {
public:
int countSubstrings(string s) {
int n = s.size();
int res = 0;
for (int i = 0; i < 2 * n - 1; i++) {
int l = i / 2, r = i / 2 + i % 2; // 这一块不太容易想到
while (l >= 0 && r < n && s[l] == s[r]) {
res++;
l--;
r++;
}
}
return res;
}
};
或者分两种情况处理
class Solution {
public:
int countSubstrings(string s) {
int result = 0;
for (int i = 0; i < s.size(); i++) {
result += extend(s, i, i, s.size()); // 以i为中心
result += extend(s, i, i + 1, s.size()); // 以i和i+1为中心
}
return result;
}
int extend(const string& s, int i, int j, int n) {
int res = 0;
while (i >= 0 && j < n && s[i] == s[j]) {
i--;
j++;
res++;
}
return res;
}
};
5. 最长回文子串
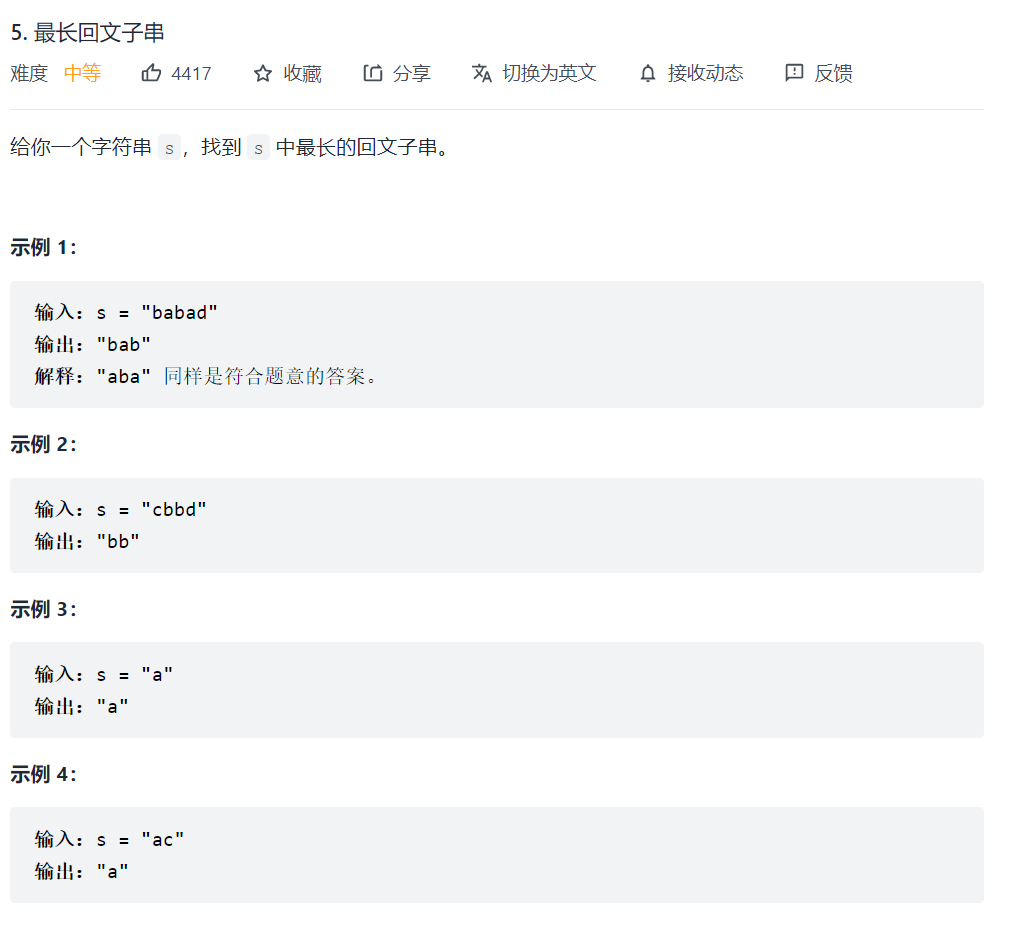

如果 “aba”是回文串,那么”babab”也一定是回文串
记P(i, j)表示字符串中 s[i]到s[j]是否为回文串,那么有以下几种情况
假设下标没有越界
- s[i] == s[j] :
- p(i + 1, j - 1) 是回文串:true
- p(i + 1, j - 1)不是回文串:false
- s[i] != s[j] : false
考虑特殊情况,一个字符是回文串,两个字符只要相等也是回文串
我们可以遍历不同长度的串,并记录最长的字串长度和起始下标
动态规划
class Solution {
public:
string longestPalindrome(string s) {
int n = s.size();
if (n < 2) return s;
vector<vector<bool>> dp(n, vector<bool>(n, false)); // dp[i][j]表示 s[i]...s[j]是否为回文串
for (int i = 0; i < n; ++i) {
dp[i][i] = true; // 长度为1的都是回文串
}
int maxLen = 1, begin = 0; // 记录最长回文子串的长度和起始索引
for (int len = 2; len <= n; ++len) { // 遍历长度
for (int i = 0; i < n; ++i) { // 遍历左下标
int j = i + len - 1; // 右下标
if (j >= n) break;
if (s[i] != s[j]) {
dp[i][j] = false;
} else {
if (len <= 3) { // 如果子串的长度小于等于3: 两个相等字符的子串是回文,两边相等中间夹一个,也是回文子串
dp[i][j] = true;
} else {
dp[i][j] = dp[i + 1][j - 1];
}
}
if (maxLen < len && dp[i][j]) { // 更新最长回文子串
maxLen = len;
begin = i;
}
}
}
return s.substr(begin, maxLen);
}
};
647题动态规划版本修改:
class Solution {
public:
string longestPalindrome(string s) {
int n = s.size();
vector<vector<bool>> dp(n, vector<bool>(n, false));
int maxLen = 0, start = 0;
for (int i = n - 1; i >= 0; i--) {
for (int j = i; j < n; j++) {
if (s[i] == s[j]) {
if (j - i <= 1 || dp[i + 1][j - 1] == true) {
dp[i][j] = true;
if (j - i + 1 > maxLen) {
maxLen = j - i + 1;
start = i;
}
}
}
}
}
return s.substr(start, maxLen);
}
};

中心扩展算法
可以由长度为1或2的回文子串向两边扩展,即从回文中心像两端扩展,扩展到不再是回文串为止,记录回文串的起始坐标,遍历每个回文中心,查找最长回文子串
class Solution {
public:
pair<int, int> expandAroundCenter(const string& s, int left, int right) {
while (left >= 0 && right < s.size() && s[left] == s[right]) {
--left;
++right;
}
return {left + 1, right - 1};
}
string longestPalindrome(string s) {
int start = 0, end = 0;
for (int i = 0; i < s.size(); ++i) {
auto [left1, right1] = expandAroundCenter(s, i, i);
auto [left2, right2] = expandAroundCenter(s, i, i + 1);
if (right1 - left1 > end - start) {
start = left1;
end = right1;
}
if (right2 - left2 > end - start) {
start = left2;
end = right2;
}
}
return s.substr(start, end - start + 1);
}
};
647题的简单修改:
class Solution {
public:
string longestPalindrome(string s) {
int n = s.size();
int start = 0, end = 0;
for (int i = 0; i < 2 * n - 1; i++) {
int l = i / 2, r = i / 2 + i % 2;
while (l >= 0 && r < n && s[l] == s[r]) {
if (r - l > end - start) {
start = l;
end = r;
}
l--;
r++;
}
}
return s.substr(start, end - start + 1);
}
};
516. 最长回文子序列
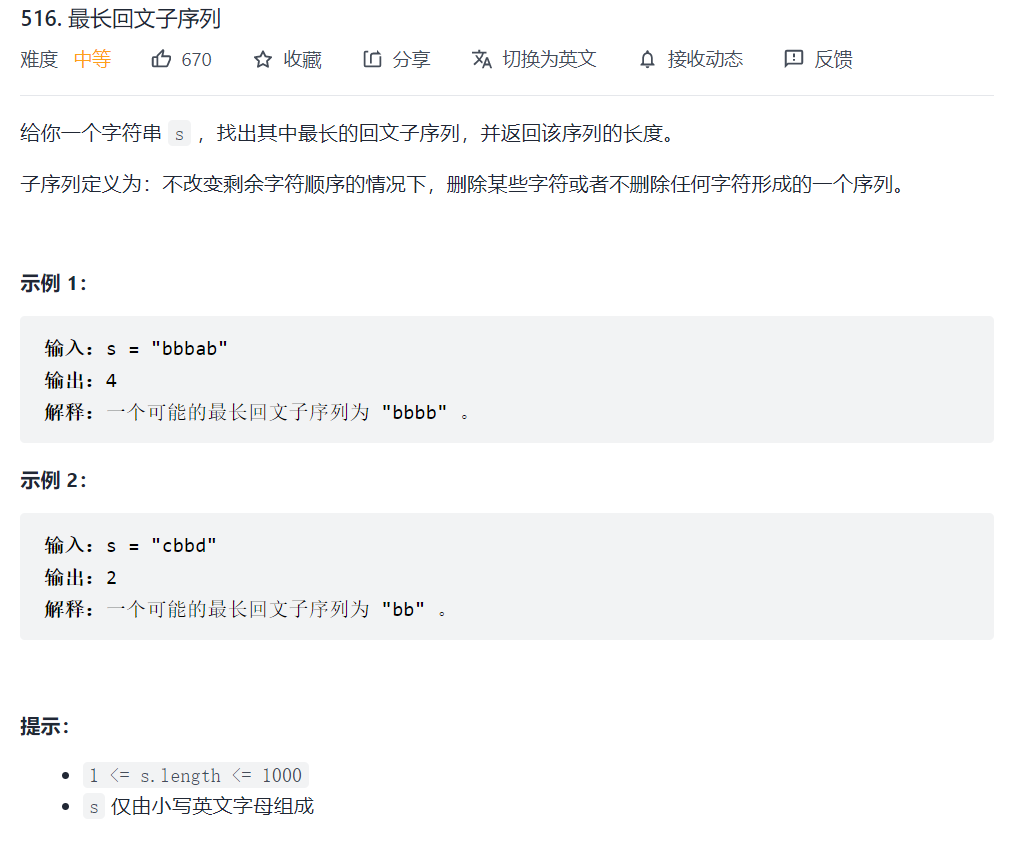
注意,子串是连续的,子序列不一定连续
但是思路大致是一样的
dp[i][j]:字符串s在[i, j]范围内最长的回文子序列的长度为dp[i][j]。
- 如果s[i]与s[j]相同,那么dp[i][j] = dp[i + 1][j - 1] + 2;
- 如果s[i]与s[j]不相同,说明s[i]和s[j]的同时加入 并不能增加[i,j]区间回文子串的长度,那么分别加入s[i]、s[j]看看哪一个可以组成最长的回文子序列。
- 加入s[j]的回文子序列长度为dp[i + 1][j]。
- 加入s[i]的回文子序列长度为dp[i][j - 1]。
那么dp[i][j]一定是取最大的,即:dp[i][j] = max(dp[i + 1][j], dp[i][j - 1]);
遍历顺序同样是从下到上,从左到右
初始化,i与j相同时,回文子序列的长度应该是1,因为通过dp[i][j] = dp[i + 1][j - 1] + 2知道,遍历不到i和j相同的情况,因此把i和j相同的情况初始化为1
class Solution {
public:
int longestPalindromeSubseq(string s) {
int n = s.size();
vector<vector<int>> dp(n, vector<int>(n, 0));
for (int i = 0; i < n; i++) dp[i][i] = 1;
for (int i = n - 1; i >= 0; i--) {
for (int j = i + 1; j < n; j++) {
if (s[i] == s[j]) {
dp[i][j] = dp[i + 1][j - 1] + 2; // 收缩
} else {
dp[i][j] = max(dp[i + 1][j], dp[i][j - 1]); // 收缩
}
}
}
return dp[0][n - 1];
}
};

回文子串的问题,因为子串是连续的所以可以用中心扩展法枚举;对于子序列问题来说,因为不一定连续,所以是没有办法用中心扩展算法的,考虑使用动态规划解决。
10. 正则表达式匹配💦
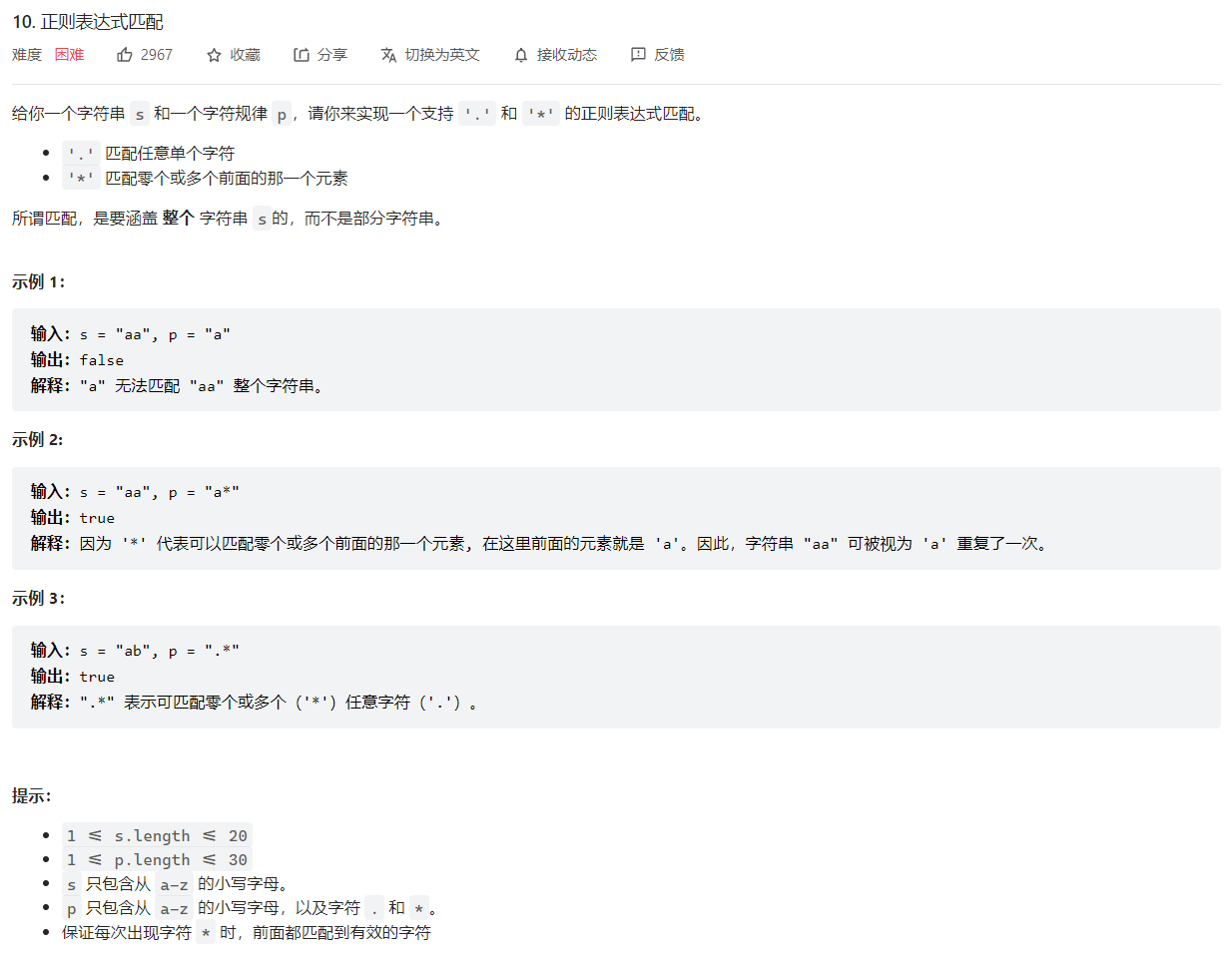
动态规划。这里的匹配时完全匹配而不是部分匹配。
记dp[i][j]表示s的前i个字符和p的前j个字符是否匹配
与下标对应后 s[0]~s[i - 1] 和 p[0] ~p[j - 1]是否匹配。
下面分情况讨论:
- p[j - 1]不是* :
- p[j - 1] == p[i - 1] 或 p[j - 1]是 ‘.’时,能够实现p[j - 1] == s[i - 1],这时有 dp[i][j] = dp[i - 1][j - 1]
- 否则 p[j - 1] != s[i - 1]: dp[i][j] = false
- p[j - 1]是:p[j - 2]和p[j - 1]假设为”a“是一个整体,不管使用多少个(0个或者多个)a,状态转移时始终保持模式串位置不变。下面根据p[j - 2]和s[i - 1]是否匹配分为两种情况
- 字符没匹配上:只能看删除p[j - 2]能否匹配: dp[i][j] = dp[i][j - 2]
- p[j - 2]和s[j - 1]匹配上:如果p[j - 2] = ‘.’或者p[j - 2] = s[i - 1]。因为p[j - 2]和p[j - 1]是一个整体,所以dp[i][j] 取决于dp[i - 1][j]。当然即使p[j - 2]能够与s[i - 1]匹配上,我们也可以将p[j - 2]删除,所以 dp[i][j] = dp[i - 1][j] || dp[i][j - 2]
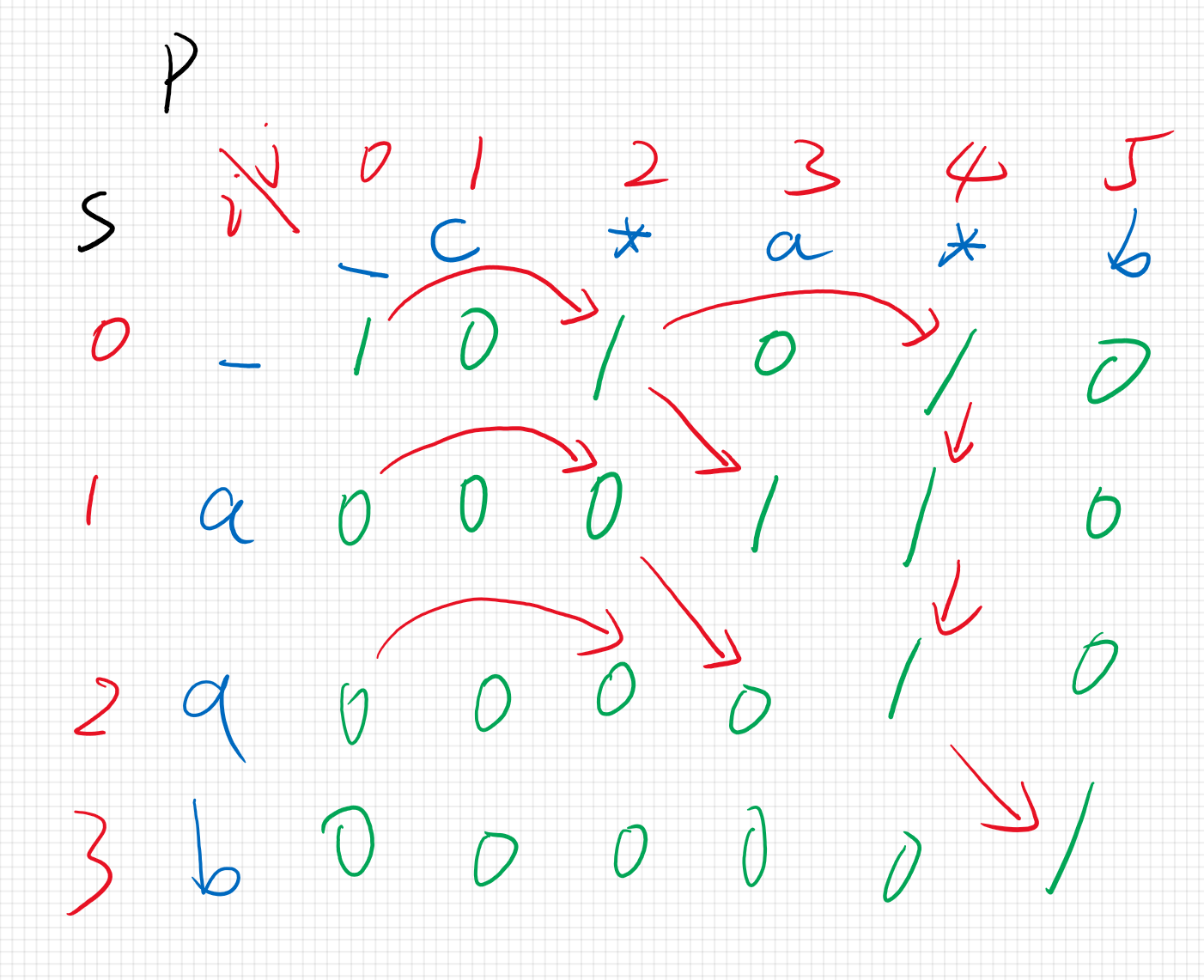
初始化:字母和’.’都不能与空串匹配,’*’可以删除前一个字符
class Solution {
public:
bool isMatch(string str, string pattern) {
int n1 = str.size(), n2 = pattern.size();
vector<vector<bool>> dp(n1 + 1, vector<bool>(n2 + 1, false));
// 初始化
dp[0][0] = true; // 空串和空串相匹配
for (int i = 2; i <= n2; i++) {
if (pattern[i - 1] == '*') { // 如果是*号考虑将前一个字符删除是否能是空串
dp[0][i] = dp[0][i - 2];
}
} // 剩余情况,无论是字母还是.都无法与空串匹配,已经默认初始化为false
// 遍历
for (int i = 1; i <= n1; i++) {
for (int j = 1; j <= n2; j++) {
// 按照p[j - 1]是不是* 分类讨论
if (pattern[j - 1] == '*') {
if (j >= 2) {
// 看删掉前一个字符能够匹配
if (pattern[j - 2] == '.' || pattern[j - 2] == str[i - 1]) {
// dp[i - 1][j]: p[j - 2]和s[i - 1]是相等的,可以考虑用*复制一个p[i - 2]
// dp[i][j - 2]: 将p[j - 2]删掉能否匹配呢?
dp[i][j] = dp[i - 1][j] || dp[i][j - 2];
} else {
dp[i][j] = dp[i][j - 2];
}
}
} else { // 不是*
if (str[i - 1] == pattern[j - 1] || pattern[j - 1] == '.') { // 两个字符能够匹配
dp[i][j] = dp[i - 1][j - 1];
}
}
}
}
return dp[n1][n2];
}
};
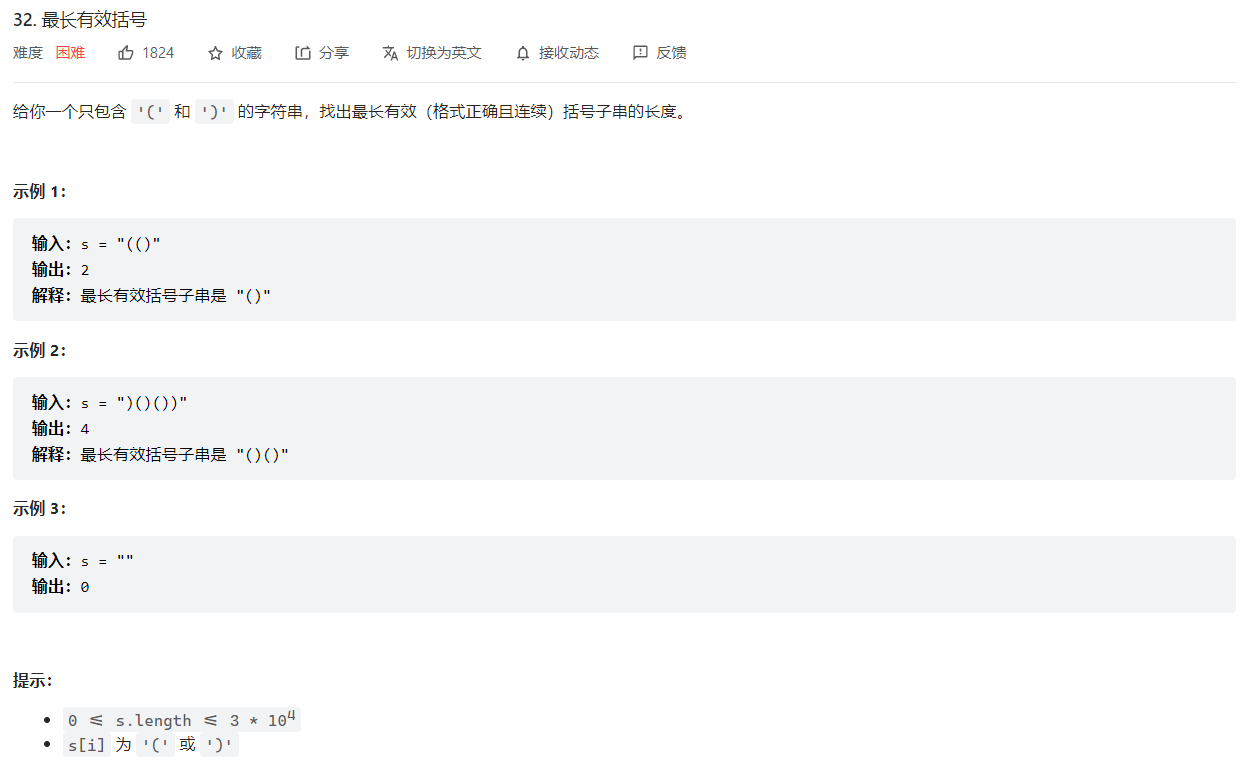
32. 最长有效括号
动态规划
记dp[i]为以s[i]为结尾的最长有效括号长度,那么:
- 如果
s[i]是左括号,以左括号为结尾的子串括号必然无效,dp[i] = 0 - 如果
s[i]是右括号,那么要根据前一个字符是左括号还是右括号讨论:- 如果
s[i - 1]是左括号,那么s[i - 1]和s[i]能够凑出一对有效括号因此dp[i] = dp[i - 2] + 2 - 如果s[i - 1]是右括号,要看一下以
s[i - 1]为结尾的有效括号有多长,记为len然后通过下标i - len - 1找到这个有效括号的前一个字符s[i - len - 1],让s[i]尝试与其匹配,如果能够匹配上,那么dp[i] = dp[i - 1] + 2,最后,要加上s[i - len - 1]前面的有效括号长度,形成总有效括号长度。
- 如果
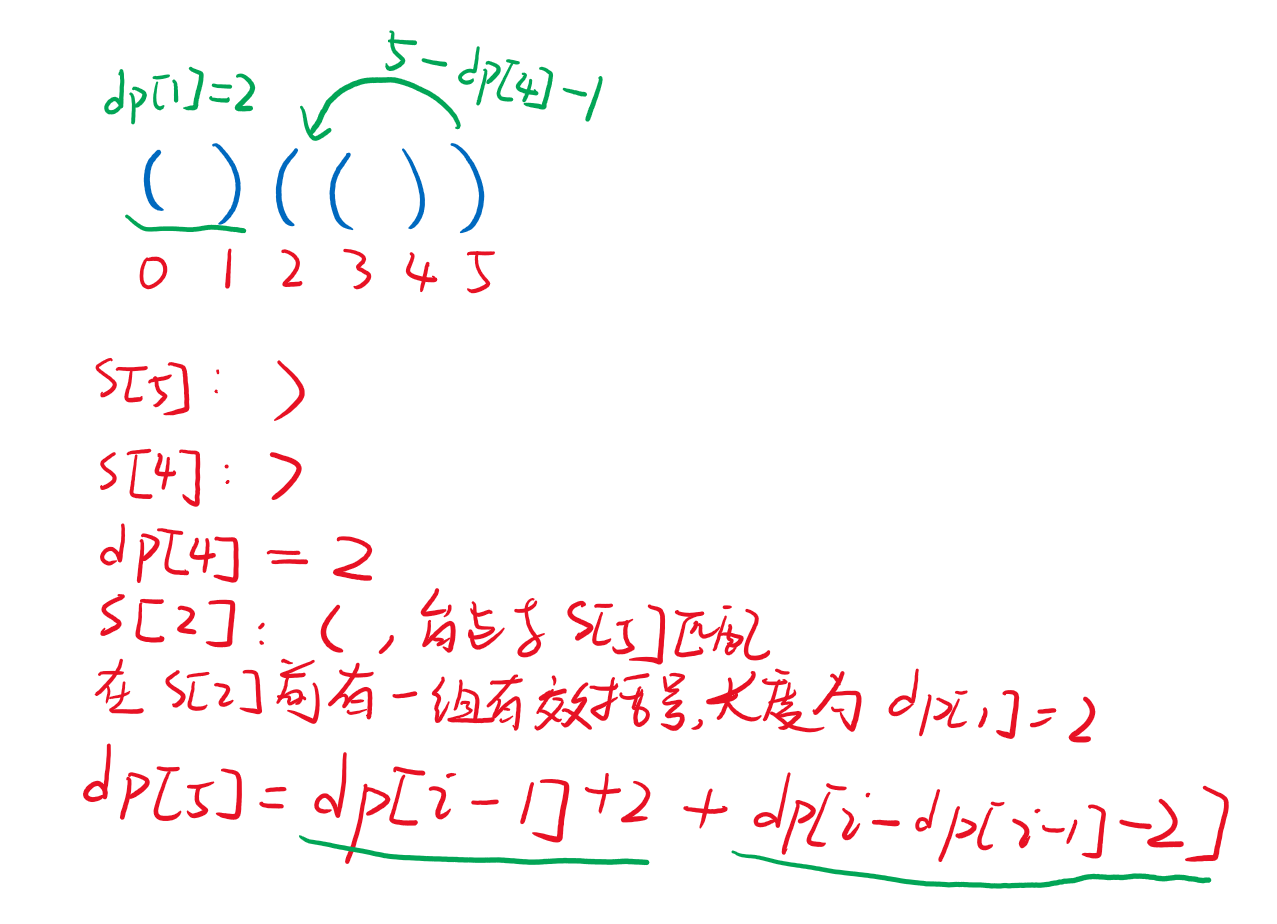
然后注意递推的时候考虑边界条件,不要让数组越界就可以了
class Solution {
public:
int longestValidParentheses(string s) {
if (s.size() < 2) return 0;
int n = s.size();
int res = 0;
vector<int> dp(n, 0);
for (int i = 1; i < n; i++) { // 以第一个字符为结尾的必是0
if (s[i] == ')') {
if (s[i - 1] == '(') { // 前一个字符为左括号
dp[i] = i >= 2 ? dp[i - 2] + 2 : 2;
} else { // 前一个字符为右括号
int len = dp[i - 1]; // 以前一个字符为结尾的最长有效括号长度
int idx = i - len - 1; // 有效括号的前一个位置
if (idx >= 0 && s[idx] == '(') {
dp[i] = dp[i - 1] + 2;
dp[i] += idx > 0 ? dp[idx - 1] : 0; // 总有效括号长度
}
}
}
res = max(res, dp[i]);
}
return res;
}
};
- 时间复杂度O(N)
- 空间复杂度O(N)
栈
维护一个栈,使栈底的元素始终是最后一个未被匹配的右括号的下标,作为当前这个有效括号的起点前一个元素(分隔符),以后每碰到一个右括号,因为栈顶的下标后一个元素是现在这一组有效括号的起点,那么可以通过i - st.top()来计算有效括号的长度。栈顶没有匹配到的左括号也可以作为分隔符,式i - st.top()依然成立。
遍历字符串
- 如果碰到左括号,将其下标压入栈中
- 如果是右括号,先将栈顶元素弹出(如果弹出的是左括号,那么相当于两者匹配上了,如果弹出的是右括号,相当于将分隔符更新为i)
分析完了以后,其实可以发现,栈中元素只能底部有一个右括号,其他的都是还未被匹配的左括号。
为了保证栈底始终是最后一个未被匹配的右括号下标的特点,记s[-1]为右括号,先将-1压入栈中
class Solution {
public:
int longestValidParentheses(string s) {
if (s.size() < 2) return 0;
stack<int> st;
st.push(-1);
int res = 0;
for (int i = 0; i < s.size(); i++) {
if (s[i] == '(') {
st.push(i);
} else {
st.pop();
if (st.empty()) {
st.push(i);
} else {
res = max(res, i - st.top());
}
}
}
return res;
}
};
- 时间复杂度O(N)
-
双指针、贪心(最优解)
用两个指针left和right分别记录左右括号的数量,如果二者数量相同,那么说明当前扫描的这一段的括号匹配是合法的。
正向遍历字符串: 碰到左括号,left++
- 碰到右括号,right++
如果左右括号数量相等,那么记录有效括号的长度,如果右括号数量大于左括号,那么重新计数将left、和right置零,表示前面那一段扫描结束。
根据上面的判断逻辑可能会忽略”(()”这种左括号数量始终大于右括号数量的情况,因此可以反向再遍历一次,让左括号去匹配右括号
class Solution {
public:
int longestValidParentheses(string s) {
if (s.size() < 2) return 0;
int n = s.size(), l = 0, r = 0, res = 0;
for (int i = 0; i < n; i++) {
s[i] == '(' ? l++ : r++;
if (l == r) res = max(res, 2 * r);
if (r > l) {
l = 0;
r = 0;
}
}
l = 0;
r = 0;
for (int i = n - 1; i >= 0; i--) {
s[i] == '(' ? l++ : r++;
if (l == r) res = max(res, 2 * l);
if (l > r) {
l = 0;
r = 0;
}
}
return res;
}
};
- 时间复杂度O(N)
- 空间复杂度O(1)