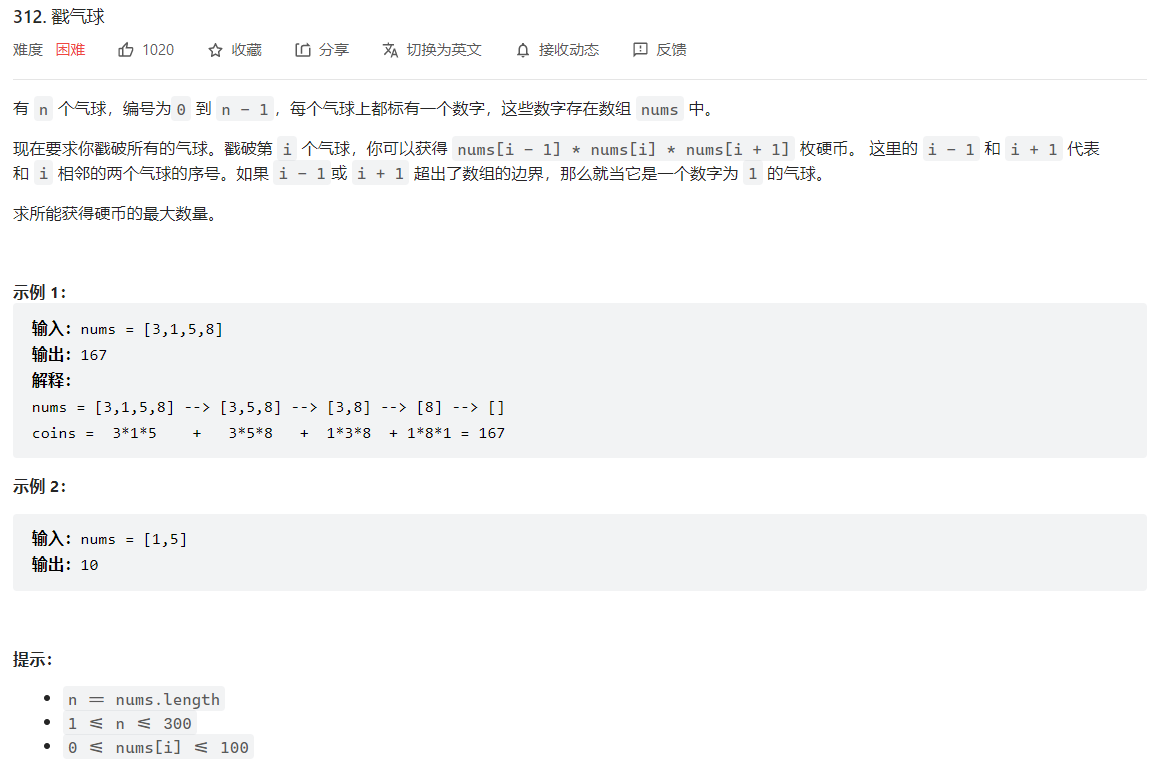
312. 戳气球

image.png

记忆化搜索

因为模拟插破气球的过程要处理不相邻的数组元素，因此从无到有插入气球，先插入的相当于是后插破的

  1. class Solution {
  2. public:
  3.     vector<vector<int>> dp;
  4.     vector<int> val;
  6.     int solve(int l, int r) {
  7.         if (l >= r - 1) return 0; // 最少有俩气球才能在中间插入一个
  8.         if (dp[l][r] != -1) return dp[l][r];
  9.         for (int i = l + 1; i < r; i++) { // 枚举气球的插入位置
  10.             int sum = val[i] * val[l] * val[r];
  11.             sum += solve(l, i) + solve(i, r);
  12.             dp[l][r] = max(dp[l][r], sum); // 记录不同插入位置的最大值 
  13.         }
  14.         return dp[l][r];
  15.     }
  17.     int maxCoins(vector<int>& nums) {
  18.         int n = nums.size();
  19.         val.resize(n + 2); // 再两端点插入值为1的气球，方便处理边界问题
  20.         dp.resize(n + 2, vector<int>(n + 2, -1));
  22.         for (int i = 1; i <= n; i++) val[i] = nums[i - 1];
  23.         val[0] = val[n + 1] = 1;
  24.         return solve(0, n + 1); // 返回在0到n+1之间插满气球的最大结果
  25.     }
  26. };

区间dp

按照记忆化搜索的思路，可以进行自底向上推导
记dp[i][j]表示填满开区间(i, j)得到的最大硬币数
image.png
我们要保证计算时用的dp[i][k]是算过的，因此区间应该从小往大枚举

  1. class Solution {
  2. public:
  3.     int maxCoins(vector<int>& nums) {
  4.         int n = nums.size();
  5.         vector<int> val(n + 2, 1); // 再两端点插入值为1的气球，方便处理边界问题
  6.         vector<vector<int>> dp(n + 2, vector<int>(n + 2, 0));
  7.         for (int i = 1; i <= n; i++) val[i] = nums[i - 1];
  8.         for (int i = n - 1; i >= 0; i--) { // 枚举区间左端点
  9.             for (int j = i + 2; j <= n + 1; j++) { // 枚举右端点
  10.                 for (int k = i + 1; k < j; k++) { // 枚举插入位置
  11.                     int sum = val[i] * val[k] * val[j];
  12.                     sum += dp[i][k] + dp[k][j];
  13.                     dp[i][j] = max(sum, dp[i][j]);
  14.                 }
  15.             }
  16.         }
  18.         return dp[0][n + 1]; // 返回在0到n+1之间插满气球的最大结果
  19.     }
  20. };

如果想要第一层循环从小到大枚举，那么第一层循环应该是枚举右端点，因为要保证先计算小区间

  1. class Solution {
  2. public:
  3.     int maxCoins(vector<int>& nums) {
  4.         int n = nums.size();
  5.         vector<int> val(n + 2, 1);
  6.         vector<vector<int>> dp(n + 2, vector<int>(n + 2, 0));
  7.         for (int i = 1; i <= n; i++) val[i] = nums[i - 1];
  9.         for (int j = 1; j <= n + 1; j++) { // 枚举右端点
  10.             for (int i = j - 2; i >= 0; i--) { // 枚举左端点
  11.                 for (int k = i + 1; k < j; k++) { // 枚举插入位置
  12.                     int sum = val[i] * val[k] * val[j];
  13.                     sum += dp[i][k] + dp[k][j];
  14.                     dp[i][j] = max(sum, dp[i][j]);
  15.                 }
  16.             }
  17.         }
  18.         return dp[0][n + 1];
  19.     }
  20. };