长度最小的子数组

209. 长度最小的子数组

暴力法

两个循环，不断寻找符合条件的子串 时间 O(n^2) 空间 O(1)

class Solution {
public:
    int minSubArrayLen(int target, vector<int>& nums) {
        //时间 O(n^2) 空间 O(1)
        int n = nums.size();
        int result = INT32_MAX;
        for (int i = 0; i < n; ++i) {
            int sum = 0, len = 0; //记录当前子串的和与当前串的长度
            for (int j = i; j < n; ++j) {
                sum += nums[j];
                len++;
                if (sum >= target) {
                    result = min(len, result);
                    break;//找到最短的就返回
                } //如果当前串的和满足要求，更新最短子串长
            }
        }
        return result == INT32_MAX ? 0 : result; //如果没有更新最短子串长度说明，无解
    }
};

滑动窗口

接下来就开始介绍数组操作中另一个重要的方法：滑动窗口。
所谓滑动窗口，就是不断的调节子序列的起始位置和终止位置，从而得出我们要想的结果。
这里还是以题目中的示例来举例，s=7， 数组是 2，3，1，2，4，3，来看一下查找的过程

最后找到 4，3 是最短距离。
其实从动画中可以发现滑动窗口也可以理解为双指针法的一种！只不过这种解法更像是一个窗口的移动，所以叫做滑动窗口更适合一些。
在本题中实现滑动窗口，主要确定如下三点：

• 窗口内是什么？
• 如何移动窗口的起始位置？
• 如何移动窗口的结束位置？

窗口就是 满足其和 ≥ s 的长度最小的 连续 子数组。
窗口的起始位置如何移动：如果当前窗口的值大于s了，窗口就要向前移动了（也就是该缩小了）。
窗口的结束位置如何移动：窗口的结束位置就是遍历数组的指针，窗口的起始位置设置为数组的起始位置就可以了。
解题的关键在于 窗口的起始位置如何移动，如图所示：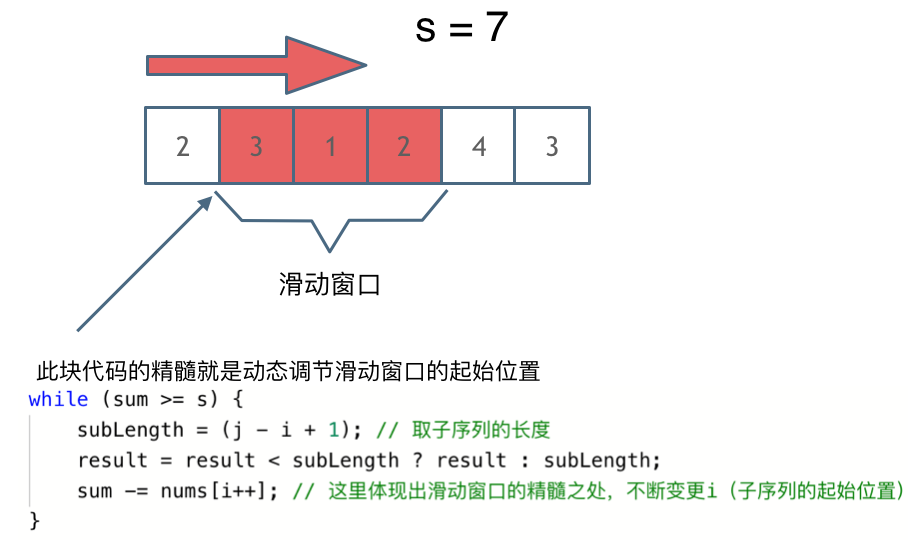

可以发现滑动窗口的精妙之处在于根据当前子序列和大小的情况，不断调节子序列的起始位置。从而将O(n^2)的暴力解法降为O(n)。

class Solution {
public:
    int minSubArrayLen(int target, vector<int>& nums) {
        //时间 O(n) 空间 O(1)
        int result = INT32_MAX;
        //滑动窗口
        int sum= 0;
        int i = 0; //窗口的起始位置
        int subLen = 0;
        for (int j = 0; j < nums.size(); ++j) {
            sum += nums[j];
            while (sum >= target) {//子数组满足长度了,开始滑
                subLen = j - i + 1; //获取窗口的长度
                result = min(result, subLen);
                sum -= nums[i++];
            }
        }
         return result == INT32_MAX ? 0 : result;
    }
};

class Solution {
public:
    int minSubArrayLen(int target, vector<int>& nums) {
        int window = 0, minLen = INT32_MAX;
        int len = 0;
        for (int i = 0, j = 0; i < nums.size(); ++i) {
            window += nums[i];
            ++len;
            // 窗口满足条件 大于等于 target时
            while (window >= target) {
                minLen = min(minLen, len);
                window -= nums[j++];
                --len;
            }      
        }
        return minLen == INT32_MAX ? 0 : minLen;
    }
};

可见，时间差的有点多呀，滑动窗口yyds！

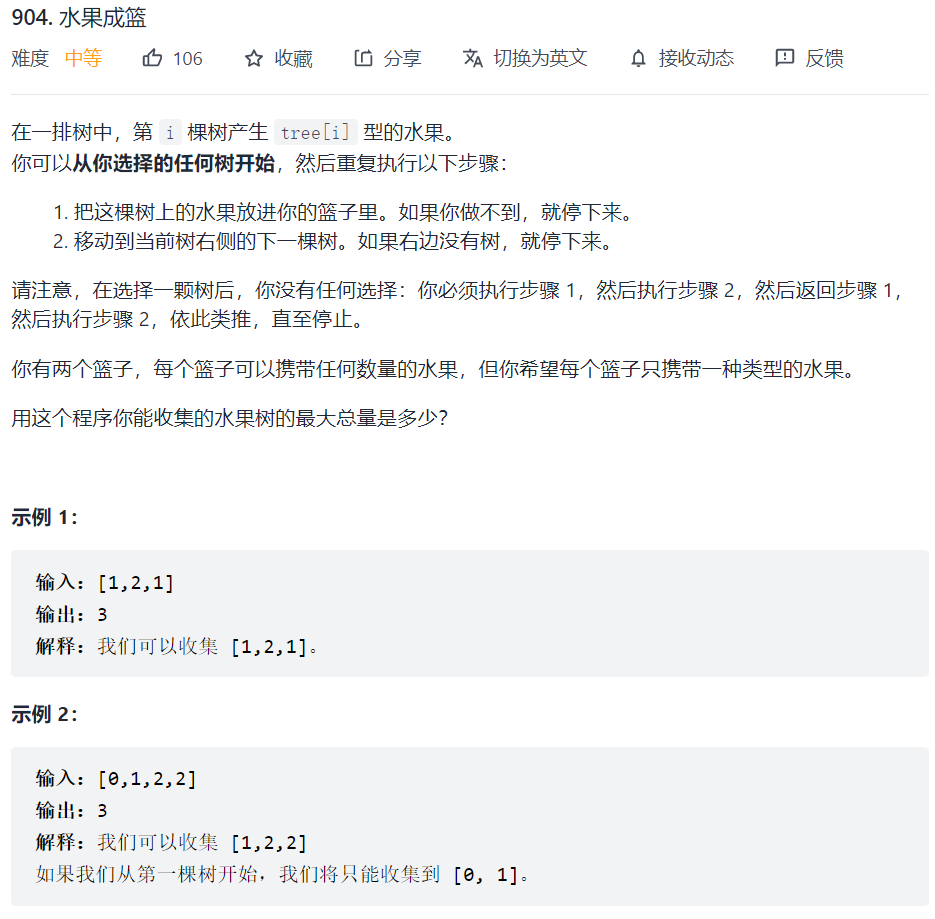
904. 水果成篮

滑动窗口

这道题可以理解为是求窗口中最多含有两个数字的最大窗口长度，因此可以用一个map来当做两个篮子，记录窗口中已经有的数字类型，如果数字多于2，则开始滑动窗口，如果map[i]的值为0，将其从map中删去

class Solution {
public:
    int totalFruit(vector<int>& fruits) {
        unordered_map<int, int> basket;
        int res = 0;
        for (int i = 0, j = 0; j < fruits.size(); ++j) {
            basket[fruits[j]]++;
            while (basket.size() > 2) {
                basket[fruits[i]]--;
                if (basket[fruits[i]] == 0) {
                    basket.erase(fruits[i]);
                }
                i++;
            }
            res = max(res, j - i + 1);
        }
        return res;
    }
};

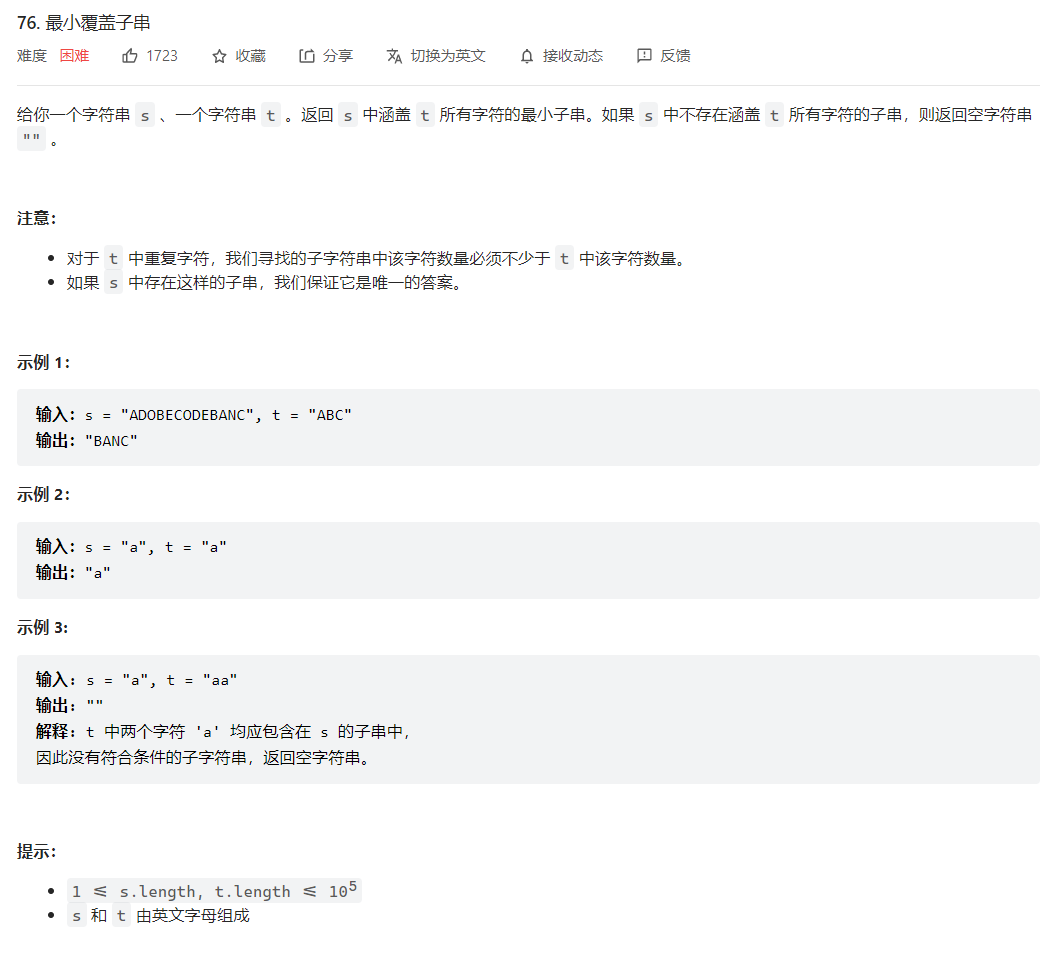
76. 最小覆盖子串

滑动窗口

O(n)O(n)
这道题要求我们返回字符串 s中包含字符串 t 的全部字符的最小窗口，我们利用滑动窗口的思想解决这个问题。因此我们需要两个哈希表，hs哈希表维护的是s字符串中滑动窗口中各个字符出现多少次，ht哈希表维护的是t字符串各个字符出现多少次。如果hs哈希表中包含ht哈希表中的所有字符，并且对应的个数都不小于ht哈希表中各个字符的个数，那么说明当前的窗口是可行的，可行中的长度最短的滑动窗口就是答案。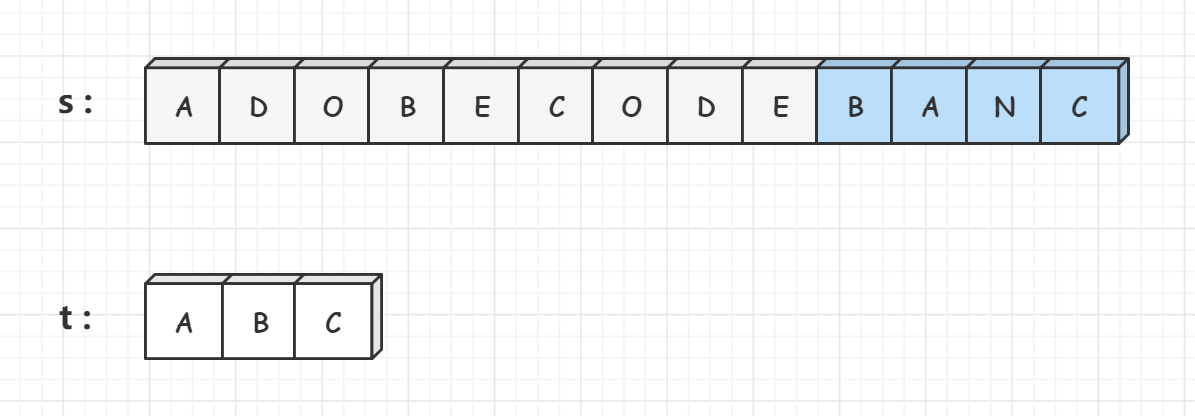

过程如下：
1、遍历t字符串，用ht哈希表记录t字符串各个字符出现的次数。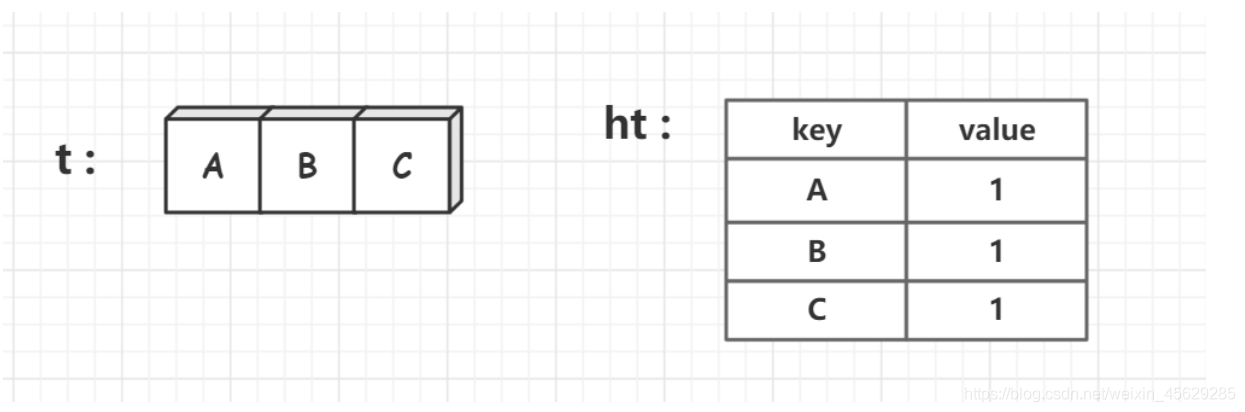

2、定义两个指针j和i，j指针用于收缩窗口，i指针用于延伸窗口，则区间[j,i]表示当前滑动窗口。首先让i和j指针都指向字符串s开头，然后枚举整个字符串s ，枚举过程中，不断增加i使滑动窗口增大，相当于向右扩展滑动窗口。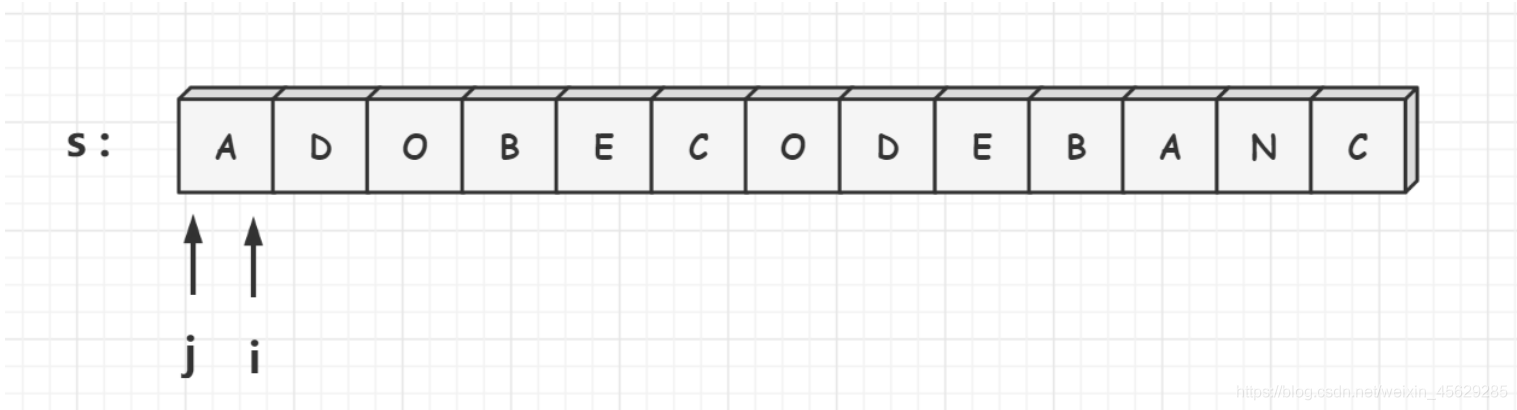

3、每次向右扩展滑动窗口一步，将s[i]加入滑动窗口中，而新加入了s[i]，相当于滑动窗口维护的字符数加一，即hs[s[i]]++。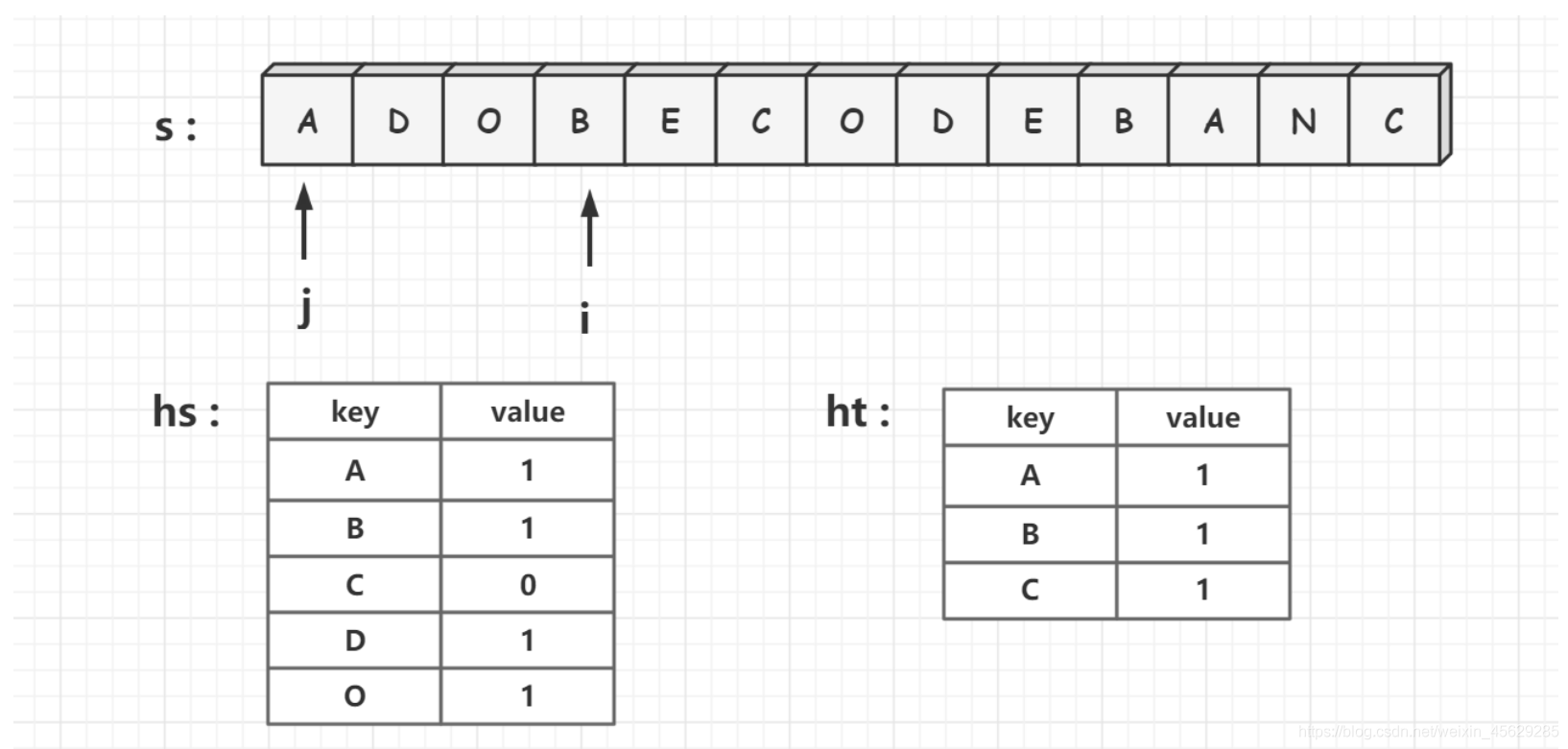

4、对于新加入的字符s[i],如果hs[s[i]] <= ht[s[i]]，(加入s[i]以后才比较，所以取等号)说明当前新加入的字符s[i]是必需的，且还未到达字符串t所要求的数量。我们还需要事先定义一个cnt变量， cnt维护的是s字符串[j,i]区间中满足t字符串的元素的个数，记录相对应字符的总数。新加入的字符s[i]必需，则cnt++。
cnt其实就是有效有效加入的个数，当有效加入达到t的长度时，此窗口有效，可以将窗口的字符串保留

5、我们向右扩展滑动窗口的同时也不能忘记收缩滑动窗口。因此当hs[s[j]] > ht[s[j]时，说明hs哈希表中s[j]的数量多于ht哈希表中s[j]的数量，此时我们就需要向右收缩滑动窗口，j++并使hs[s[j]]—，
即hs[s[j ++ ]] --。
6、当cnt == t.size时，说明此时滑动窗口包含符串 t 的全部字符。我们重复上述过程找到最小窗口即为答案。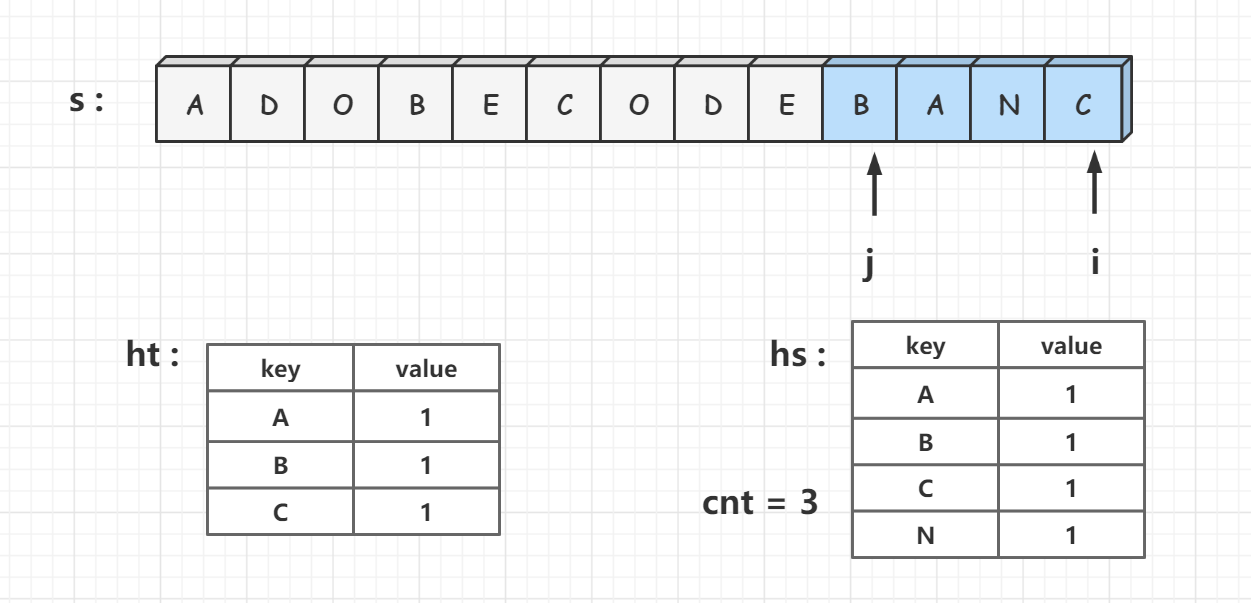

class Solution {
public:
    string minWindow(string s, string t) {
        unordered_map<char, int> hs, ht;
        for (auto c : t) ht[c]++;
        string res;
        int cnt = 0;
        for (int i = 0, j = 0; i < s.size(); i++) {
            hs[s[i]]++;
            if (hs[s[i]] <= ht[s[i]]) cnt++; // 有效加入
            while (hs[s[j]] > ht[s[j]]) hs[s[j++]]--; //滑动窗口
            if (cnt == t.size()) {
                if (res.empty() || i - j + 1 < res.size())
                    res = s.substr(j, i - j + 1);
            }

        }
        return res;
    }
};