121. 买卖股票的最佳时机

暴力会超时

贪心

股票只有一支，那么取左端的最小值，右端的最大值，就可以获得最大利润

class Solution {
public:
    int maxProfit(vector<int>& prices) {
        int low = 10010;
        int res = 0;
        for (auto price : prices) {
            low = min(low, price); // 记住最小值
            res = max(res, price - low); // 如果能够取得更大的利润，那么更新利润
        }
        return res;
    }
};

• 时间复杂度：O(n)
• 空间复杂度：O(1)

动态规划

记dp[0][i]表示第i天持有股票的最大现金，dp[1][i]表示第i天不持有股票的最大现金
如果第i天持有股票：

• dp[0][i] = dp[0][i - 1]，第i-1天手中就持有股票
• dp[0][i] = - price[i]，今天买入股票

那么dp[0][i] = max( dp[0][i - 1], - price[i])

如果第i天没有股票：

• dp[1][i] = dp[0][i - 1] + prices[i]，第i-1天手中持有股票，今天给卖了
• dp[1][i] = dp[1][i - 1]，前一天也没有股票，保持现状

那么dp[1][i] = max( dp[0][i - 1] + prices[i]，dp[1][i - 1])

初始化：dp[0][0] = -prices[0] 第一天买入股票；dp[1][0] = 0, 第一天没有股票

class Solution {
public:
    int maxProfit(vector<int>& prices) {
        int n = prices.size();
        vector<vector<int>> dp(2, vector<int>(n, 0));
        dp[0][0] = -prices[0];
        for (int i = 1; i < n; i++) {
            dp[0][i] = max(dp[0][i - 1], -prices[i]);
            dp[1][i] = max(dp[1][i - 1], dp[0][i - 1] + prices[i]);
        }
        return dp[1][n - 1];
    }
};

• 时间复杂度O(n)
• 空间复杂度O(n)

优化空间复杂度：

class Solution {
public:
    int maxProfit(vector<int>& prices) {
        int n = prices.size();
        int num1 = -prices[0], num2 = 0;
        for (int i = 1; i < n; i++) {
            int tmp = num1;
            num1 = max(num1, -prices[i]); // 价格低，那么相反数大，以较低价格买入
            num2 = max(num2, tmp + prices[i]);
        }
        return num2;
    }
};

122. 买卖股票的最佳时机 II

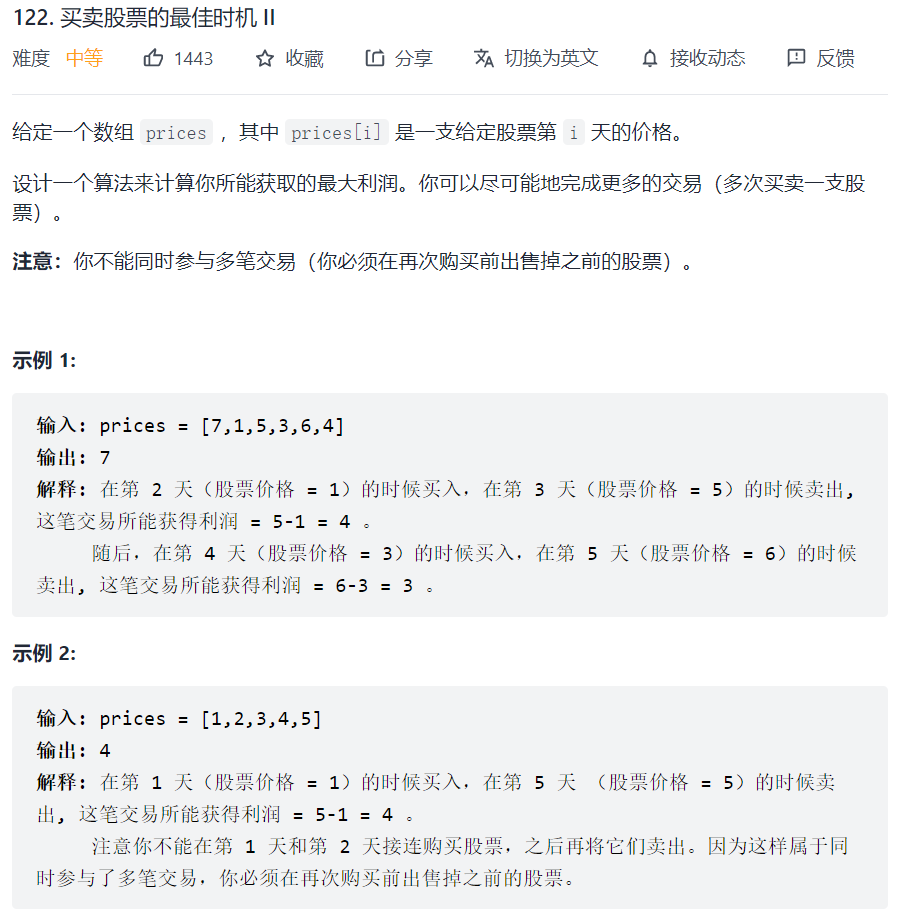
本题首先要清楚两点：

• 只有一只股票！
• 当前只有买股票或者卖股票的操作

想获得利润至少要两天为一个交易单元。

贪心

第i天买入，第i+1天卖出，利润为：

第i天买入，第i+n天卖出，利润为:

可以见得，第i天买第i+n天卖所得利润和这几天每天进行买卖利润和累加，结果是一样的，因此可以只考虑今天和明天是否能挣钱即可。如果明天比今天贵，挣钱，就今天买了明天卖，如果今天比明天贵，亏钱，那么今天不买。将每一份挣的钱累加起来，就是最大利润

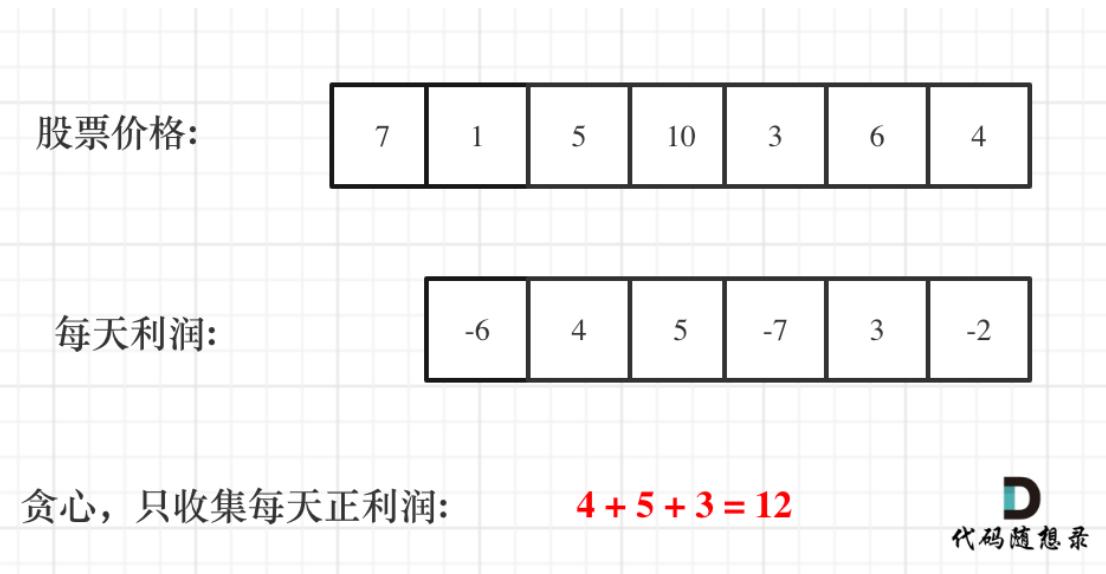
class Solution {
public:
    int maxProfit(vector<int>& prices) {
        int res = 0;
        for (int i = 1; i < prices.size(); i++) {
            res += max(prices[i] - prices[i - 1], 0); // 将能够挣钱的交易
        }
        return res;
    }
};

时间复杂度O(n)，空间复杂度O(1)

动态规划

不能同时参与多笔交易，因此每天交易结束后，只可能存在两种状态：

• 手中有一只股票
• 手中没有股票

定义dp[0][i]表示第i天手中没有股票获得的最大利润，dp[1][i]表示第i天手中有股票时的获得的最大利润
为了利益最大化，有如下状态转移方程：

取前一天也没有股票的利润、前一天手中有股票今天将股票出售后的利润的最大值

取前一天也手持股票的利润、前一天手中没有股票今天买入股票后的利润的最大值

初始化，根据题意dp[0][0] = 0，dp[1][0] = -prices[0]

最后获得利润手中一定没有股票，那么dp[0][n-1]就是利润的最大值

class Solution {
public:
    int maxProfit(vector<int>& prices) {
        int n = prices.size();
        vector<vector<int>> dp(2, vector<int>(n, 0));
        dp[0][0] = 0;
        dp[1][0] = -prices[0];
        for (int i = 1; i < n; i++) {
            dp[0][i] = max(dp[0][i - 1], dp[1][i - 1] + prices[i]);
            dp[1][i] = max(dp[1][i - 1], dp[0][i - 1] - prices[i]);
        }
        return dp[0][n - 1];
    }
};

当天结束后的利润只由前一天决定，因此用两个变量来记录前一天结束后的利润就可以优化空间复杂度

class Solution {
public:
    int maxProfit(vector<int>& prices) {
        int a = 0, b = -prices[0];
        for (int i = 1; i < prices.size(); i++) {
            int tmp = a;
            a = max(a, b + prices[i]);
            b = max(b, tmp - prices[i]);
        }
        return a;
    }
};

时间复杂度O(n)，空间复杂度O(n)，优化后空间复杂度为O(1)

123. 买卖股票的最佳时机 III

可以进行两笔交易，那么可以将每天的情况分解为五种状态：

• 没有操作
• 第一次买入
• 第一次卖出
• 第二次买入
• 第二次卖出

dp[i][j]中 i表示第i天，j为 [0 - 4] 五个状态，dp[i][j]表示第i天状态j所剩最大现金。状态代表的是持有股票与否，并不是买入和卖出股票

分情况讨论状态转移：

• dp[i][1]: 前一天没有操作或者前一天已经第一次持有，dp[i][1] = max(dp[i - 1][1], dp[i - 1][0] - prices[i])
• dp[i][2]: 前一天持有第一次购买的股票今天卖出 或者 之前股票已经被卖出保持状态 dp[i][2] = max(dp[i - 1][2], dp[i - 1][1] + prices[i]);
• dp[i][3]: 之前已经买入第二支股票，保持状态，或者今天买入第二支股票 dp[i][3] = max(dp[i - 1][3], dp[i - 1][2] - prices[i]);
• dp[i][4]: 之前已经卖出第二支股票，保持状态，或者今天卖出第二支股票 dp[i][4] = max(dp[i - 1][4], dp[i - 1][3] + prices[i]);

初始化：
第0天没有操作，就是0，即：dp[0][0] = 0;
第0天做第一次买入的操作，dp[0][1] = -prices[0];
第0天做第一次卖出的操作，dp[0][2] = 0; 买了再卖，获利为0
第0天第二次买入操作，dp[0][3] = -prices[0]; 第一次买卖操作后，再买入
第0天做第二次卖出的操作，dp[0][2] = 0; 第二次买了再卖，获利为0

第 i 天的状态由第 i-1 天推出来，因此要从前向后遍历

class Solution {
public:
    int maxProfit(vector<int>& prices) {
        int n = prices.size();
        vector<vector<int>> dp(n, vector<int>(5, 0));
        dp[0][1] = -prices[0]; // 第一次买入
        dp[0][3] = -prices[0]; // 第二次买入
        for (int i = 1; i < n; i++) {
            dp[i][0] = dp[i - 1][0];// 保持无操作
            dp[i][1] = max(dp[i - 1][1], dp[i - 1][0] - prices[i]);
            dp[i][2] = max(dp[i - 1][2], dp[i - 1][1] + prices[i]);
            dp[i][3] = max(dp[i - 1][3], dp[i - 1][2] - prices[i]);
            dp[i][4] = max(dp[i - 1][4], dp[i - 1][3] + prices[i]);
        }
        return dp[n - 1][4];
    }
};

通过状态转移方程，发现当天状态只与前一天有关，因此可以用大小为5的数组记录状态，或者五个变量（麻烦）

class Solution {
public:
    int maxProfit(vector<int>& prices) {
        int n = prices.size();
        vector<int> dp(5, 0);
        dp[1] = -prices[0]; // 第一次买入
        dp[3] = -prices[0]; // 第二次买入
        for (int i = 1; i < n; i++) {
            // dp[0] = dp[0];// 保持无操作
            dp[1] = max(dp[1], dp[0] - prices[i]);
            dp[2] = max(dp[2], dp[1] + prices[i]);
            dp[3] = max(dp[3], dp[2] - prices[i]);
            dp[4] = max(dp[4], dp[3] + prices[i]);
        }
        return dp[4];
    }
};

维护五个变量：
初始状态不用维护，4个变量就够了

class Solution {
public:
    int maxProfit(vector<int>& prices) {
        int n = prices.size();
        // int a = 0; // 初始状态
        int buy1 = -prices[0], sell1 = 0; // 第一次买卖
        int buy2 = -prices[0], sell2 = 0; // 第二次买卖
        for (int i = 1; i < n; i++) {
            buy1 = max(buy1, -prices[i]); // 之前已经买入第一次或者今天买入第一次
            sell1 = max(sell1, buy1 + prices[i]);
            buy2 = max(buy2, sell1 - prices[i]);
            sell2 = max(sell2, buy2 + prices[i]);
        }
        return sell2;
    }
};

188. 买卖股票的最佳时机 IV

将买卖股票的最佳时机Ⅲ的代码稍作修改
一次交易代表一个买入和一个买出操作，再加上一个无操作，一共 2 k + 1 个状态，因此dp数组的维度可以定义为(n, 2 k + 1)

class Solution {
public:
    int maxProfit(int k, vector<int>& prices) {
        if (prices.size() == 0) return 0;
        vector<vector<int>> dp(prices.size(), vector<int>(2 * k + 1, 0));
        for (int j = 1; j < 2 * k; j += 2) {
            dp[0][j] = -prices[0];
        }
        for (int i = 1;i < prices.size(); i++) {
            for (int j = 0; j < 2 * k - 1; j += 2) {
                dp[i][j + 1] = max(dp[i - 1][j + 1], dp[i - 1][j] - prices[i]);
                dp[i][j + 2] = max(dp[i - 1][j + 2], dp[i - 1][j + 1] + prices[i]);
            }
        }
        return dp[prices.size() - 1][2 * k];
    }
};

维护一个pair数组或者两个数组，或者一个2*（k+1）的数组：
pair:

• first:记录第j次buy状态
• second：记录第j次sell状态

那么在处理到第i天时，当天的prices为prices[i],循环处理每一次交易，

• 第 j 次buy状态都可能由第 i-1 天的第 j 次buy状态、第 i-1 天的第 j-1 次sell状态+购买股票转移来
• 第 j 次sell状态都可能由第 i-1 天的第 j 次sell状态、第 i-1 天的第 j-1 次buy状态+卖出股票转移来

因为每次迭代新的一天的时候，dp数组的状态都是上一天每次交易对应的结果，因此状态转移方程为：

• dp[j].first = max(dp[j].first, dp[j - 1].second - prices[i])
• dp[j].second = max(dp[j].second, dp[j - 1].first + prices[i])

  class Solution {
  public:
    int maxProfit(int k, vector<int>& prices) {
        if (prices.size() == 0) return 0;
        int n = prices.size();
        vector<pair<int, int>> dp(k + 1, {0, 0}); // 维护k对变量，first持股buy second不持股sell
        for (int i = 1; i <= k; i++) dp[i].first = -prices[0];
        for (int i = 1; i < n; i++) {
            for (int j = 1; j <= k; j++) {
                dp[j].first = max(dp[j].first, dp[j - 1].second - prices[i]);
                dp[j].second = max(dp[j].second, dp[j].first + prices[i]);
            }
        }
        return dp[k].second;
    }
  };
  

309. 最佳买卖股票时机含冷冻期

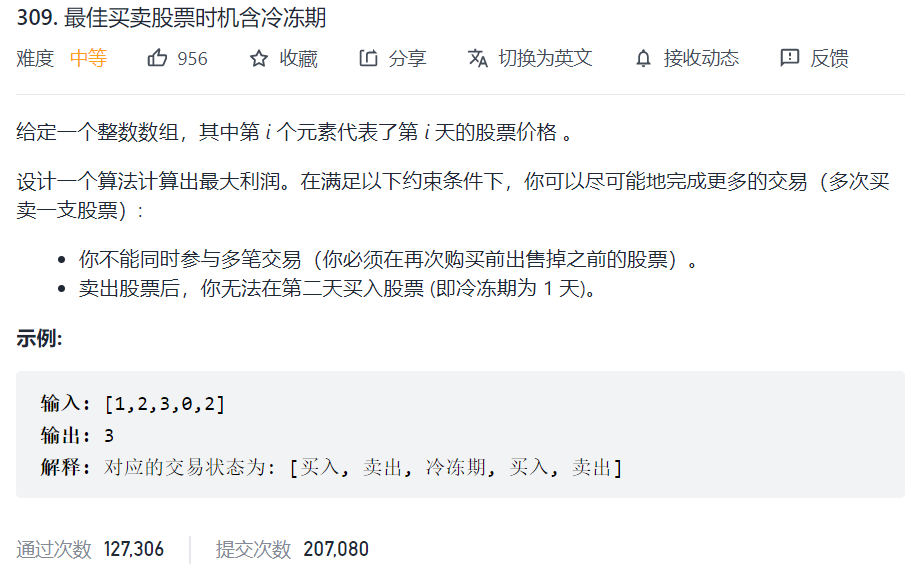
状态转移：

三个状态:

• 0：手中持有股票
• 1：手中不持有股票，处于冷却期
• 2：手中不持有股票且不是冷却期

dp[i][0]：今天买入，昨天不能是冷却期；或者本来就持有 dp[i][0] = max(dp[i - 1][0], dp[i-1][2] - prices[i])
dp[i][1]: 手中没有股票，进入冷却期，只能是前一天有股票，今天卖了：dp[i][1] = dp[i - 1][0] + prices[i]
dp[i][2]：手中没有股票，且不是冷却期，本来就是这个状态或者前一天处于冷却期(前一天卖了股票，今天什么也不操作) dp[i][2] = max(dp[i - 1][1], dp[i - 1][2])
最后返回没有股票的状态的最大值：即 max(dp[i][1], dp[i][2])

class Solution {
public:
    int maxProfit(vector<int>& prices) {
        if (prices.empty()) return 0;
        int n = prices.size();
        vector<vector<int>> dp(3, vector<int>(n, 0));
        dp[0][0] = -prices[0];
        for (int i = 1; i < n; ++i) {
            dp[0][i] = max(dp[0][i - 1], dp[2][i - 1] - prices[i]);
            dp[1][i] = dp[0][i - 1] + prices[i];
            dp[2][i] = max(dp[1][i - 1], dp[2][i - 1]);
        }
        return max(dp[1][n - 1], dp[2][n - 1]);
    }
};

优化空间后：

class Solution {
public:
    int maxProfit(vector<int>& prices) {
        if (prices.empty()) return 0;
        int a = -prices[0], b = 0, c = 0;
        for (int i = 1; i < prices.size(); ++i) {
            int tmp1 = max(a, c - prices[i]);
            int tmp2 = a + prices[i];
            int tmp3 = max(b, c);
            a = tmp1;
            b = tmp2;
            c = tmp3;
        }
        return max(b, c);
    }
};

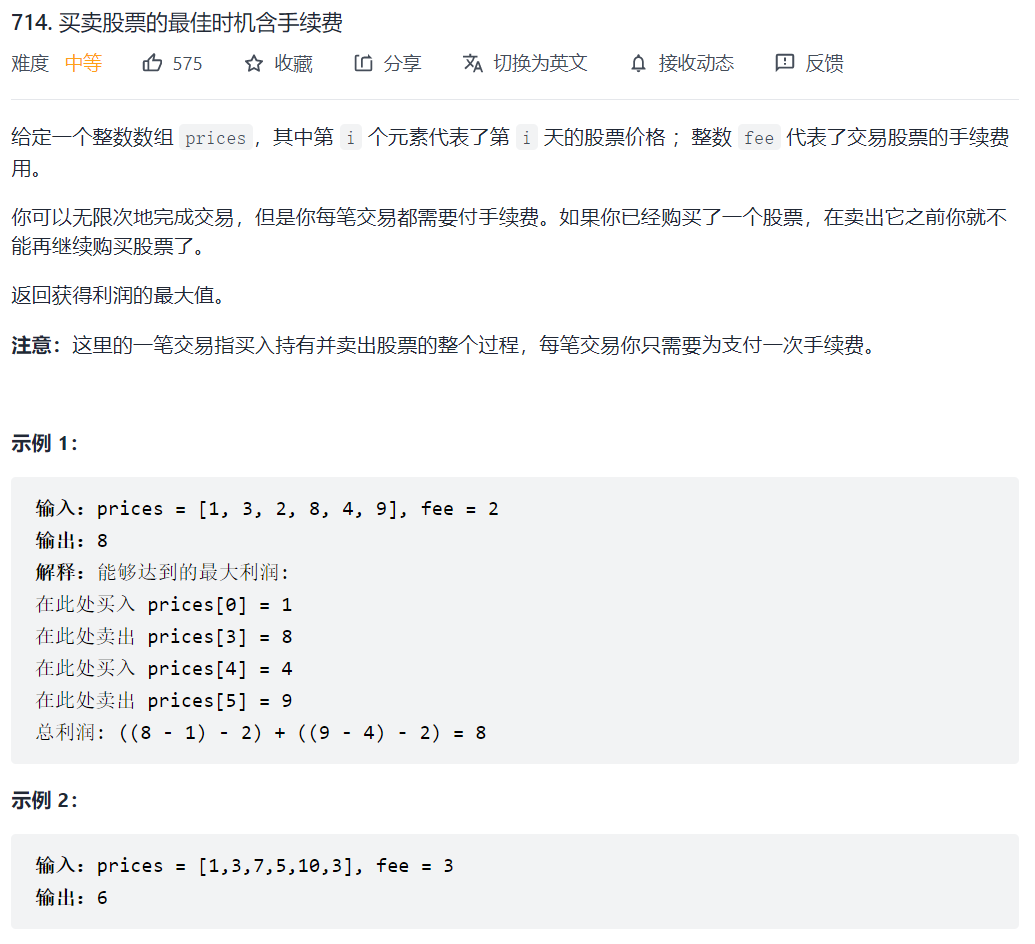
714. 买卖股票的最佳时机含手续费

贪心💦

如果换一个角度考虑，将手续费放在买入时进行计算，那么就可以得到一种基于贪心的方法。

用 buy 表示在最大化收益的前提下，如果我们手上拥有一支股票，那么它的最低买入价格是多少。在初始时，buy 的值为 prices[0] 加上手续费 fee。那么当我们遍历到第 i (i>0) 天时：

• 如果当前的股票价格 prices[i] 加上手续费fee 小于 buy，那么与其使用 buy 的价格购买股票，我们不如以 prices[i]+fee 的价格购买股票，因此我们将 buy 更新为prices[i]+fee；
• 如果当前的股票价格prices[i] 大于 buy，那么我们直接卖出股票并且获得 prices[i]−buy 的收益。但实际上，我们此时卖出股票可能并不是全局最优的（例如下一天股票价格继续上升），因此我们可以提供一个反悔操作，看成当前手上拥有一支买入价格为 prices[i] 的股票，将 buy 更新为prices[i]。这样一来，如果下一天股票价格继续上升，我们会获得prices[i+1]−prices[i] 的收益，加上这一天 prices[i]−buy 的收益，恰好就等于在这一天不进行任何操作，而在下一天卖出股票的收益；
• 对于其余的情况，prices[i] 落在区间 [buy−fee,buy] 内，它的价格没有低到我们放弃手上的股票去选择它，也没有高到我们可以通过卖出获得收益，因此我们不进行任何操作。

上面的贪心思想可以浓缩成一句话，即当我们卖出一支股票时，我们就立即获得了以相同价格并且免除手续费买入一支股票的权利。在遍历完整个数组 prices 之后之后，我们就得到了最大的总收益。

作者：LeetCode-Solution 链接：https://leetcode-cn.com/problems/best-time-to-buy-and-sell-stock-with-transaction-fee/solution/mai-mai-gu-piao-de-zui-jia-shi-ji-han-sh-rzlz/ 来源：力扣（LeetCode） 著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

总结官方题解的贪心法，是将股票的购买价格加上手续费，作为真正的购买价格，为了使利益最大化，选择购买价格最低的那天买入股票，如果可以获利，卖出的价格大于买入的价格，那么这一天有可能不是真正卖出的那天，因为明天股票的价格可能更高，用prices[i]减去买入价格，再将购买价格赋值为prices[i]，继续遍历，就可以累计利润，这样相当于是在价格最高的那天卖出。
推导：
假设prices，在某一天买入了股票，花费为buy，prices[i] ~ prices[j]股票价格一直在上涨，那么可以知道，在第j天卖掉股票，收益最大，最大收益为：

那么我们在i~j每天将股票卖出，在第二天将股票卖出，每天都能累计一点利润，有：

也就是官方题解中的那句话

当我们卖出一支股票时，我们就立即获得了以相同价格并且免除手续费买入一支股票的权利

继续遍历下去的话，如果后面出现了prices[x] + fee 小于 prices[j] 的情况，又可以买入股票了，如果后面还能获利，继续累加profit，这样，到最后就实现了全局最优解，利润最大

唉呀妈，贪心真复杂，这道题还是动态规划好理解一些。

动态规划

与122题类似，只不过卖出股票时需要考虑手续费
状态转移方程改为

取前一天也没有股票的利润、前一天手中有股票今天将股票出售后的利润的最大值

取前一天也手持股票的利润、前一天手中没有股票今天买入股票后的利润的最大值

C++代码：

class Solution {
public:
    int maxProfit(vector<int>& prices, int fee) {
        int n = prices.size();
        vector<vector<int>> dp(2, vector<int>(n, 0));
        // 初始化
        dp[0][0] = 0;
        dp[1][0] = -prices[0];
        for (int i = 1; i < n; i++) {
            dp[0][i] = max(dp[0][i-1], dp[1][i - 1] + prices[i] - fee);
            dp[1][i] = max(dp[0][i-1] - prices[i], dp[1][i - 1]);
        }
        return dp[0][n-1];
    }
};

同样，因为只与前一天的状态有关，那么可以用两个变量记录状态来优化空间

class Solution {
public:
    int maxProfit(vector<int>& prices, int fee) {
        int n = prices.size();
        // 初始化
        int noHave = 0;
        int have = -prices[0];
        for (int i = 1; i < n; i++) {
            int temp = noHave;
            noHave = max(noHave, have + prices[i] - fee);
            have = max(temp - prices[i], have);
        }
        return noHave;
    }
};

• 时间复杂度为O(n)
• 空间复杂度为iO(n)，优化后为O(1)

总结

股票问题两种思路：

• 贪心（少数适用）
• 动态规划（全部适用）

动态规划的思路就是定义两种状态，手中持股和手中不持股，
然后题目要求：

• 交易一次
• 交易多次
• 冷冻期
• 手续费（卖股票时减去手续费）