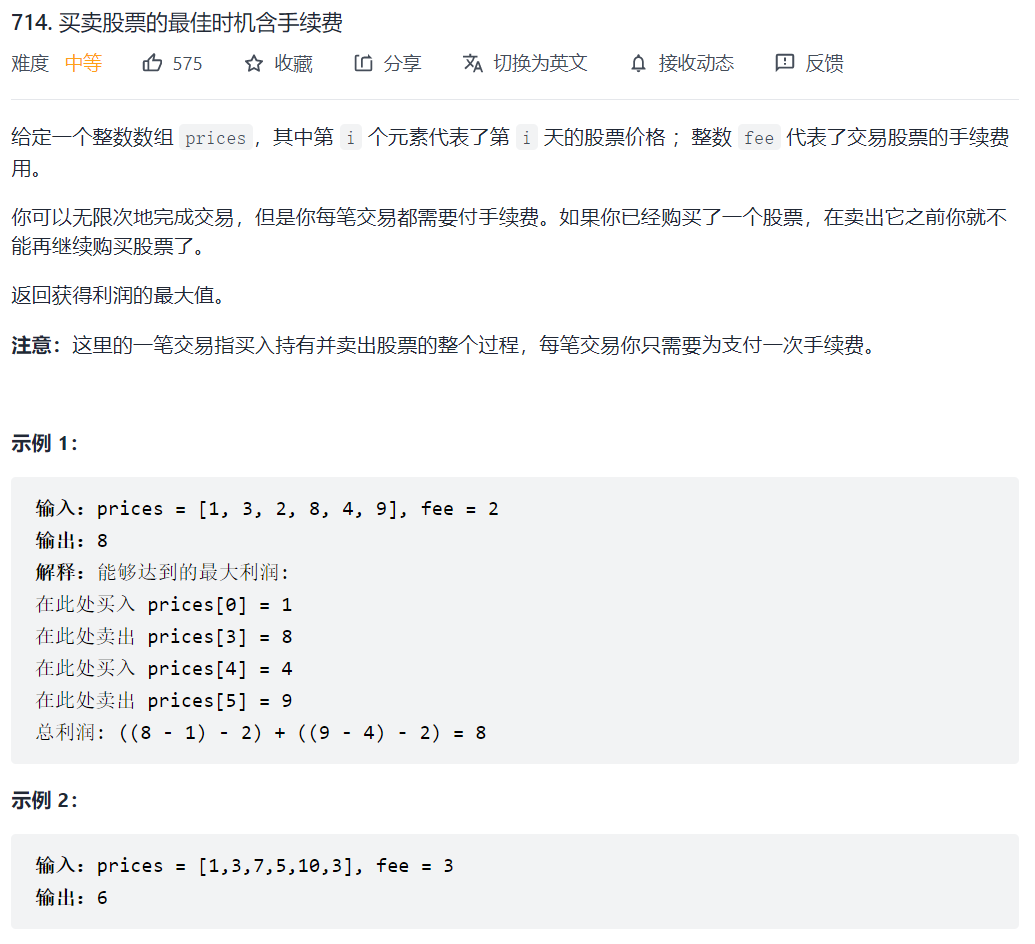
122. 买卖股票的最佳时机 II

本题首先要清楚两点：

• 只有一只股票！
• 当前只有买股票或者买股票的操作

想获得利润至少要两天为一个交易单元。

贪心

第i天买入，第i+1天卖出，利润为

第i天买入，第i+n天迈出，利润为:

也就是说利润是可以分解的，把利润分解为天的维度，这样取只考虑正利润，取正利润和，如果正利润连续，相当于是隔几天再卖出（将股票留在手里可以得到更高的利润），中间夹杂负利润，连续的负利润表示股票一直在跌，不适合买入。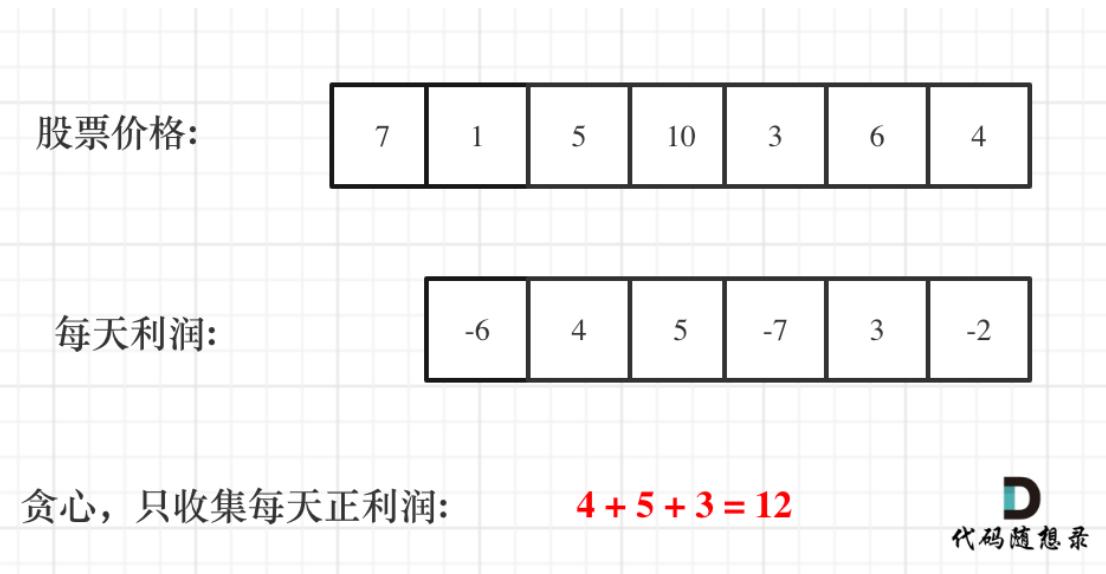

贪心的思路总结一下就是：如果今天比昨天贵就可以昨天买入今天卖出，局部最优解就是每次价格连续上升的子区间内，区间左端点买入，右端点卖出，获得这个期间内的最大利润，而这个区间内的最大利润是和从第二天起每天都执行卖出买入操作最终获得的利润是一致的，全局最优解就是最终利润最大化

class Solution {
public:
    int maxProfit(vector<int>& prices) {
        int result = 0;
        for (int i = 1; i < prices.size(); i++) {
            result += max(prices[i] - prices[i - 1], 0); // 只取正利润
        }
        return result;
    }
};

时间复杂度O(n)，空间复杂度O(1)

动态规划

不能同时参与多笔交易，因此每天交易结束后，只可能存在两种状态：

• 手中有一只股票
• 手中没有股票

定义dp[0][i]表示第i天手中没有股票获得的最大利润，dp[1][i]表示第i天手中有股票时的获得的最大利润
为了利益最大化，有如下状态转移方程：

取前一天也没有股票的利润、前一天手中有股票今天将股票出售后的利润的最大值

取前一天也手持股票的利润、前一天手中没有股票今天买入股票后的利润的最大值

初始化，根据题意dp[0][0] = 0，dp[1][0] = -prices[0]

最后获得利润手中一定没有股票，那么dp[0][n-1]就是利润的最大值

当天结束后的利润只由前一天决定，因此用两个变量来记录前一天结束后的利润就可以优化空间复杂度

class Solution {
public:
    int maxProfit(vector<int>& prices) {
        int a = 0, b = -prices[0];// 前一天手中不持股  前一天手中持股
        for (int i = 1; i < prices.size(); i++) {
            int tmp = a;
            a = max(a, b + prices[i]); // 保持现状或者将股票卖出
            b = max(b, tmp - prices[i]); // 保持现状或者今天购买股票
        }
        return a;
    }
};

时间复杂度O(n)，优化后空间复杂度为O(1)

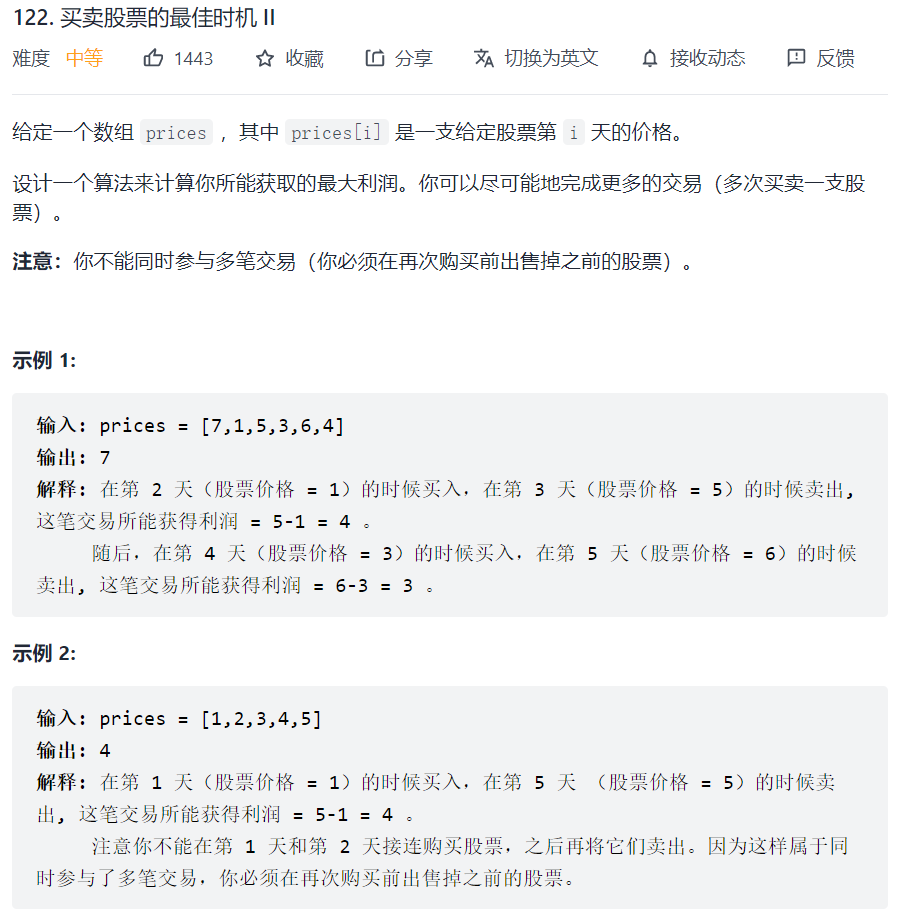
714. 买卖股票的最佳时机含手续费

贪心💦

如果换一个角度考虑，将手续费放在买入时进行计算，那么就可以得到一种基于贪心的方法。

用 buy 表示在最大化收益的前提下，如果我们手上拥有一支股票，那么它的最低买入价格是多少。在初始时，buy 的值为 prices[0] 加上手续费 fee。那么当我们遍历到第 i (i>0) 天时：

• 如果当前的股票价格 prices[i] 加上手续费fee 小于 buy，那么与其使用 buy 的价格购买股票，我们不如以 prices[i]+fee 的价格购买股票，因此我们将 buy 更新为prices[i]+fee；
• 如果当前的股票价格prices[i] 大于 buy，那么我们直接卖出股票并且获得 prices[i]−buy 的收益。但实际上，我们此时卖出股票可能并不是全局最优的（例如下一天股票价格继续上升），因此我们可以提供一个反悔操作，看成当前手上拥有一支买入价格为 prices[i] 的股票，将 buy 更新为prices[i]。这样一来，如果下一天股票价格继续上升，我们会获得prices[i+1]−prices[i] 的收益，加上这一天 prices[i]−buy 的收益，恰好就等于在这一天不进行任何操作，而在下一天卖出股票的收益；
• 对于其余的情况，prices[i] 落在区间 [buy−fee,buy] 内，它的价格没有低到我们放弃手上的股票去选择它，也没有高到我们可以通过卖出获得收益，因此我们不进行任何操作。

上面的贪心思想可以浓缩成一句话，即当我们卖出一支股票时，我们就立即获得了以相同价格并且免除手续费买入一支股票的权利。在遍历完整个数组 prices 之后之后，我们就得到了最大的总收益。

作者：LeetCode-Solution 链接：https://leetcode-cn.com/problems/best-time-to-buy-and-sell-stock-with-transaction-fee/solution/mai-mai-gu-piao-de-zui-jia-shi-ji-han-sh-rzlz/ 来源：力扣（LeetCode） 著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

总结官方题解的贪心法，是将股票的购买价格加上手续费，作为真正的购买价格，为了使利益最大化，选择购买价格最低的那天买入股票，如果可以获利，卖出的价格大于买入的价格，那么这一天有可能不是真正卖出的那天，因为明天股票的价格可能更高，用prices[i]减去买入价格，再将购买价格赋值为prices[i]，继续遍历，就可以累计利润，这样相当于是在价格最高的那天卖出。
推导：
假设prices，在某一天买入了股票，花费为buy，prices[i] ~ prices[j]股票价格一直在上涨，那么可以知道，在第j天卖掉股票，收益最大，最大收益为：

那么我们在i~j每天将股票卖出，在第二天将股票卖出，每天都能累计一点利润，有：

也就是官方题解中的那句话

当我们卖出一支股票时，我们就立即获得了以相同价格并且免除手续费买入一支股票的权利

继续遍历下去的话，如果后面出现了prices[x] + fee 小于 prices[j] 的情况，又可以买入股票了，如果后面还能获利，继续累加profit，这样，到最后就实现了全局最优解，利润最大

class Solution {
public:
    int maxProfit(vector<int>& prices, int fee) {
        int n = prices.size();
        int res = 0, buy = prices[0] + fee; // 以prices[i] + fee 的价格买一只股票
        for (int i = 1; i < n; i++) {
            if (prices[i] + fee < buy) {
                buy = prices[i] + fee; // 如果能够以更低的价格买入股票，那么更新买入的价格
            } else if (prices[i] > buy){
                res += prices[i] - buy; // 这次能够赚到钱，卖出股票
                buy = prices[i];
            }
        }
        return res;
    }
};

动态规划

与122题类似，只不过卖出股票时需要考虑手续费
状态转移方程改为

取前一天也没有股票的利润、前一天手中有股票今天将股票出售后的利润的最大值

取前一天也手持股票的利润、前一天手中没有股票今天买入股票后的利润的最大值

同样，因为只与前一天的状态有关，那么可以用两个变量记录状态来优化空间

class Solution {
public:
    int maxProfit(vector<int>& prices, int fee) {
        int n = prices.size();
        int a = 0, b = -prices[0]; // 第一天不持股 第一天持股
        for (int i = 1; i < n; i++) {
            a = max(a, b + prices[i] - fee); // 卖出股票需要支付手续费
            b = max(b, a - prices[i]);
        }
        return a; // 利润最大时手中一定不持股
    }
};

• 时间复杂度为O(n)
• 空间复杂度为O(1)