0-1背包
416. 分割等和子集💦
这道题可以换一种表述:给定一个只包含正整数的非空数组 nums[0],判断是否可以从数组中选出一些数字,使得这些数字的和等于整个数组的元素和的一半。因此这个问题可以转换成「0-1 背包问题」。这道题与传统的「0−1 背包问题」的区别在于,传统的「0−1 背包问题」要求选取的物品的重量之和不能超过背包的总容量,这道题则要求选取的数字的和恰好等于整个数组的元素和的一半。类似于传统的「0−1 背包问题」,可以使用动态规划求解。
首先计算一下数组的和sum,如果sum/2是奇数,那么无论如何都不能将数组拆分为元素和相等的两个子集
设 sum/2 = target
然后创建二维数组dp,包含 n + 1行 target + 1 列,其中dp[i][j] 表示从数组的前i个元素中选取若干个正整数(可以是 0 个),是否存在一种选取方案使得被选取的正整数的和等于 j。初始时,dp 中的全部元素都是 false。
然后考虑 j = 0 的情况,找一些数,使它们的和为0,也就是说,一个数字也不选就能够做到,所以初始化dp[i][0] = true;
因为i表示第几个,所以访问nums中的元素要减1,当 nums[i - 1] = j 时,会用到 dp[i][0],表示可以从 1 ~ i-1 选择一些数字,其和为0,因为 j = ums[i - 1],所以只选择nums[i - 1]这一个数,便能够得到和j
状态转移方程:
- 从 0 ~ i-1 (下标)个数中选择几个数,和能为j
从 0~ i-1 (下标)中选举几个数,和为 j - nums[i - 1],都可以实现从 1 ~ i中选择几个数,和为j
class Solution {public:bool canPartition(vector<int>& nums) {int n = nums.size();if (n < 2) return false;int sum = accumulate(nums.begin(), nums.end(), 0);if (sum % 2) return false;int target = sum / 2;vector<vector<bool>> dp(n + 1, vector<bool>(target + 1, false));for (int i = 0; i <= n; i++)dp[i][0] = true; // 可以选择0个数使和为0for (int i = 1; i <= n; i++) {for (int j = 1; j <= target; j++) {if (nums[i - 1] <= j) {// 从 0 ~ i-1 个数中选择几个数,和能为j 或者 从 0 ~ i-1中选举几个数,和为j - nums[i - 1]// 都可以实现从 1 ~ i中选择几个数,和为jdp[i][j] = dp[i - 1][j] || dp[i - 1][j - nums[i - 1]];} else {dp[i][j] = dp[i - 1][j];}}}return dp[n][target];}};
用滚动数组优化空间复杂度,注意改变遍历顺序
class Solution { public: bool canPartition(vector<int>& nums) { int sum = accumulate(nums.begin(), nums.end(), 0); if (sum % 2 != 0) return false; int target = sum / 2; // 背包容量 vector<bool> dp(target + 1, false); dp[0] = true; for (auto num : nums) { for (int i = target; i >= num; --i) dp[i] = dp[i] || dp[i - num]; } return dp[target]; } };
1049. 最后一块石头的重量 II

假设将有两个堆,一正一负,根据题目中的描述,我们可以每次取两个石头,将重量较大者赋值为正,较小者赋值为负,然后二者相加
两个石头抵消,假设石头的总重量为sum,设target = sum / 2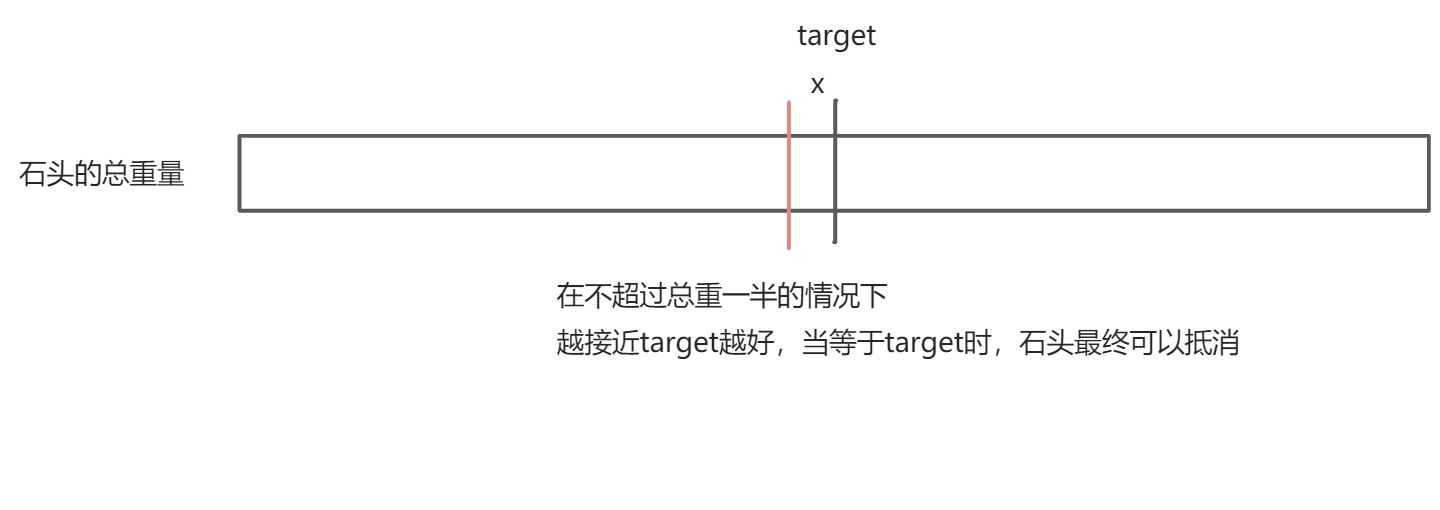
问题最终可以转换为:背包容量为target,石头的重量和价值都为stones{i],在不超过target的前提下,找石头重量和的最大值max,就是一个01背包问题
假设 target - max = x,那么石头两两相消最后剩下的部分就是 target + x - ( target - x) = 2x , 可以见得,x越小,最后剩下的重量越小。
class Solution {
public:
int lastStoneWeightII(vector<int> &stones) {
int sum = accumulate(stones.begin(), stones.end(), 0);
int target = sum / 2;
vector<int> dp(target + 1, 0);
for (int i = 0; i < stones.size(); i++) {
int s = stones[i];
for (int j = target; j >= s; j--) {
dp[j] = max(dp[j], dp[j - s] + s);
}
}
return abs(sum - dp[target] - dp[target]);
}
};
494. 目标和

01背包问题基本上都能用回溯暴力解决,但是一般都会超时,本题也不例外,所以直接上动态规划
动态规划
分析:根据题意,将数组分为两组,一组为正,一组为负,假设正数的一组和为,那么负数的一组和应为
,那么可以知道
,整理得
%22%20aria-hidden%3D%22true%22%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMATHI-70%22%20x%3D%220%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMATHI-6F%22%20x%3D%22503%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMATHI-73%22%20x%3D%22989%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMATHI-69%22%20x%3D%221458%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMATHI-74%22%20x%3D%221804%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMATHI-69%22%20x%3D%222165%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMATHI-76%22%20x%3D%222511%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMATHI-65%22%20x%3D%222996%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-3D%22%20x%3D%223740%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%3Cg%20transform%3D%22translate(4519%2C0)%22%3E%0A%3Cg%20transform%3D%22translate(397%2C0)%22%3E%0A%3Crect%20stroke%3D%22none%22%20width%3D%225914%22%20height%3D%2260%22%20x%3D%220%22%20y%3D%22220%22%3E%3C%2Frect%3E%0A%3Cg%20transform%3D%22translate(60%2C725)%22%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMATHI-73%22%20x%3D%220%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMATHI-75%22%20x%3D%22469%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMATHI-6D%22%20x%3D%221042%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-2B%22%20x%3D%222142%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMATHI-74%22%20x%3D%223143%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMATHI-61%22%20x%3D%223504%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMATHI-72%22%20x%3D%224034%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMATHI-67%22%20x%3D%224485%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMATHI-65%22%20x%3D%224966%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMATHI-74%22%20x%3D%225432%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%3C%2Fg%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-32%22%20x%3D%222706%22%20y%3D%22-687%22%3E%3C%2Fuse%3E%0A%3C%2Fg%3E%0A%3C%2Fg%3E%0A%3C%2Fg%3E%0A%3C%2Fsvg%3E#card=math&code=positive%20%3D%20%5Cfrac%7Bsum%20%2B%20target%7D%7B2%7D&id=iJvIC),那么问题就转化为,在数组中找到一组数,使得这些数的和为
。当
是奇数或者
时无解。
设表示由
这几个数中挑选一些数,能够凑成和为j的方案数,那么状态转移方程为:
前
个数能够凑出
的方案数和前
个数凑出
的方案数之和
由于只与上一行的结果有关系,可以直接写成一维的,得到状态转移方程:
记得写成一维的要反向遍历
class Solution {
public:
int findTargetSumWays(vector<int>& nums, int target) {
int s = accumulate(nums.begin(), nums.end(), 0);
// 如果abs(target) > s,那么都取正号或者都取负号也不行,返回0,要不然s + target < 0 构造dp会越界
if (abs(target) > s || (s + target) % 2) return 0;
int n = (s + target) / 2;
vector<int> dp(n + 1, 0);
dp[0] = 1; // 和为0的方案有一种,就是什么都不选
for (auto num : nums)
for (int j = n; j >= num; --j)
dp[j] += dp[j - num];
return dp[n];
}
};
注:在求装满背包有几种方法的情况下,递推公式一般为:
474. 一和零💦
01背包
本题中strs 数组里的元素就是物品,每个物品都是一个!
而m 和 n相当于是一个背包,两个维度的背包。
动规五部曲:
- 确定dp数组(dp table)以及下标的含义
dp[i][j]:最多有i个0和j个1的strs的最大子集的大小为dp[i][j]。
- 确定递推公式
dp[i][j] 可以由前一个strs里的字符串推导出来,strs里的字符串有zeroNum个0,oneNum个1。
dp[i][j] 就可以是 。
然后我们在遍历的过程中,取dp[i][j]的最大值。
所以递推公式:
此时可以回想一下01背包的递推公式:;
对比一下就会发现,字符串的zeroNum和oneNum相当于物品的重量(weight[i]),字符串本身的个数相当于物品的价值(value[i])。
这就是一个典型的01背包! 只不过物品的重量有了两个维度而已。
- dp数组如何初始化
在动态规划:01背包的dp数组初始化为0就可以。
因为物品价值不会是负数,初始为0,保证递推的时候dp[i][j]不会被初始值覆盖。
- 确定遍历顺序
在动态规划:01背包一定是外层for循环遍历物品,内层for循环遍历背包容量且从后向前遍历!
那么本题也是,物品就是strs里的字符串,背包容量就是题目描述中的m和n。
for (string str : strs) { // 遍历物品
int oneNum = 0, zeroNum = 0;
for (char c : str) {
if (c == '0') zeroNum++;
else oneNum++;
}
for (int i = m; i >= zeroNum; i--) { // 遍历背包容量且从后向前遍历!
for (int j = n; j >= oneNum; j--) {
dp[i][j] = max(dp[i][j], dp[i - zeroNum][j - oneNum] + 1);
}
}
}
有同学可能想,那个遍历背包容量的两层for循环先后循序有没有什么讲究?
没讲究,都是物品重量的一个维度,先遍历那个都行!
- 举例推导dp数组
以输入:[“10”,”0001”,”111001”,”1”,”0”],m = 3,n = 3为例
最后dp数组的状态如下所示: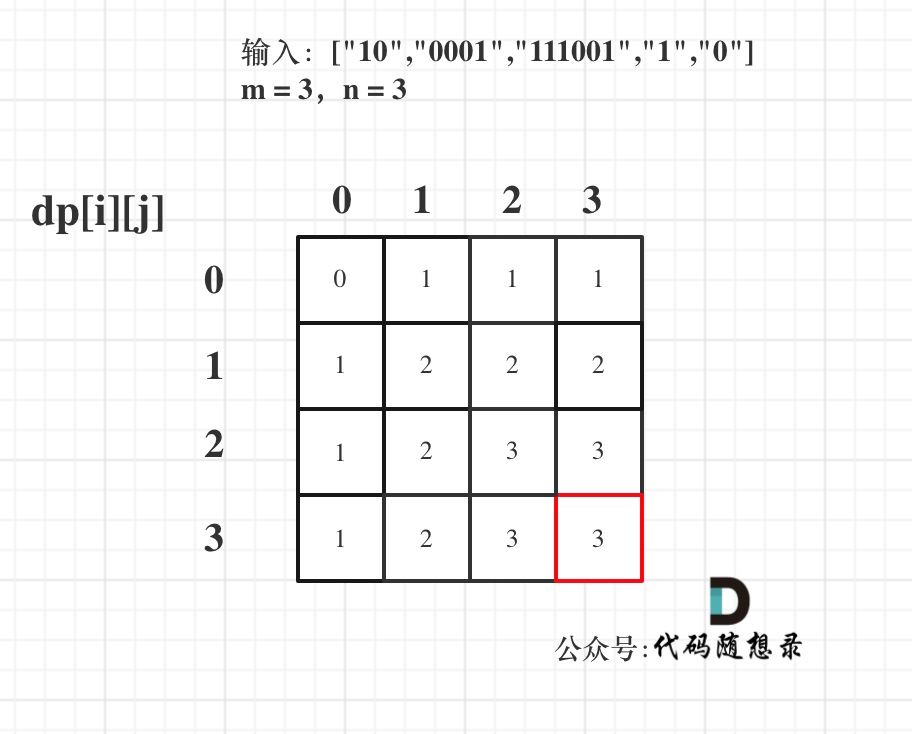
class Solution {
public:
int findMaxForm(vector<string>& strs, int m, int n) {
// dp[i][j]表示最多含有i个0和j个1的子集个数
vector<vector<int>> dp(m + 1, vector<int>(n + 1, 0));
for (auto s : strs) {
int oneNum = 0, zeroNum = 0;
for (auto c : s) {
if (c == '1') oneNum++;
else zeroNum++;
}
//遍历背包容量
for (int i = m; i >= zeroNum; i--) {
for (int j = n; j >= oneNum; j--) {
// 数组更新前保留的是上一层的结果
// 判断将当前物品(字符串)加到子集里来和不加的最大值
dp[i][j] = max(dp[i][j], dp[i - zeroNum][j - oneNum] + 1);
}
}
}
return dp[m][n];
}
};
多重背包
看作多背包问题,一个背包容量是m,一个背包容量是n,可以定义一个三维数据dp[i][j][k]
表示在前 i 个字符串中,使用 j 个 0 和 k 个 1 的情况下最多可以得到的字符串数量。假设字符串数组的长度为len,那么最终返回的结果就是dp[len][m][n]
考虑边界条件,如果i=0,表示没有字符串,那么dp[0][i][j]必然为0,对于其他的i来说,字符串数组中的第i个元素如果要放入背包,必须满足 j >= count0 且 k >= count1,所以可以得到状态转移方程
if j < count0 || k < count1:
dp[i][j][k] = dp[i - 1][j][k];
if j >= count0 && k >= count1:
dp[i][j][k] = max(dp[i - 1][j][k], dp[i - 1][j - count0][k - count1]);
可以观察到无论如何,i 的状态只与 i - 1 有关,因此还可以将三维数组压缩为二维,降低空间复杂度
//压缩以后逆向遍历
dp[i][j] = max(dp[i][j], 1 + dp[i-count0][j-count1])
// 三维dp
class Solution {
public:
int findMaxForm(vector<string>& strs, int m, int n) {
vector<vector<int>> dp(m + 1, vector<int>(n + 1, 0));
for (const string & str: strs) {
auto [count0, count1] = count(str);
for (int i = m; i >= count0; --i) {
for (int j = n; j >= count1; --j) {
dp[i][j] = max(dp[i][j], 1 + dp[i-count0][j-count1]);
}
}
}
return dp[m][n];
}
pair<int, int> count(const string & str) {
int count0 = 0, count1 = 0;
for (const auto & c : str) {
c == '0' ? ++count0 : ++count1;
}
return make_pair(count0, count1);
}
};
//二维dp
class Solution {
public:
int findMaxForm(vector<string>& strs, int m, int n) {
vector<vector<int>> dp(m + 1, vector<int>(n + 1, 0));
for (const auto & str : strs) {
auto [count0, count1] = count(str);//打包
for (int i = m; i >= count0; --i) {//反向遍历背包1的容量
for (int j = n; j >= count1; --j) {//反向遍历背包2的容量
dp[i][j] = max(dp[i][j], dp[i - count0][j - count1] + 1);
}
}
}
return dp[m][n];
}
pair<int, int> count(const string & str) {
int count0 = 0, count1 = 0;
for (const auto & c : str) {
c == '0' ? ++count0 : ++count1;
}
return make_pair(count0, count1);
}
};
完全背包问题
518. 零钱兑换 II


硬币可以取无限次,是完全背包问题。本题要求组合数,要与能够组成多少金额的问题区分开来。
记dp[j]表示,可以凑出金额为j的种类数
那么dp[0] = 1,不取硬币可以凑出总金额为0,一种,其余值都为0
状态转移方程:dp[i][j] = dp[i - 1][j] + dp[j][j - coins[i]] ,由前i-1种硬币能凑出的种类数,加上由i-1种硬币可以凑出金额 j - coins[i] 的种类数
代码:
class Solution {
public:
int change(int amount, vector<int>& coins) {
vector<int> dp(amount + 1, 0);
dp[0] = 1;
for (auto coin : coins)
for (int i = 1; i <= amount; ++i)
if (i >= coin) dp[i] += dp[i - coin];
return dp[amount];
}
};
注:背包的组合问题大多数情况下,状态转移方程都为,完全背包与01背包的遍历顺序不同罢了
377. 组合总和 Ⅳ
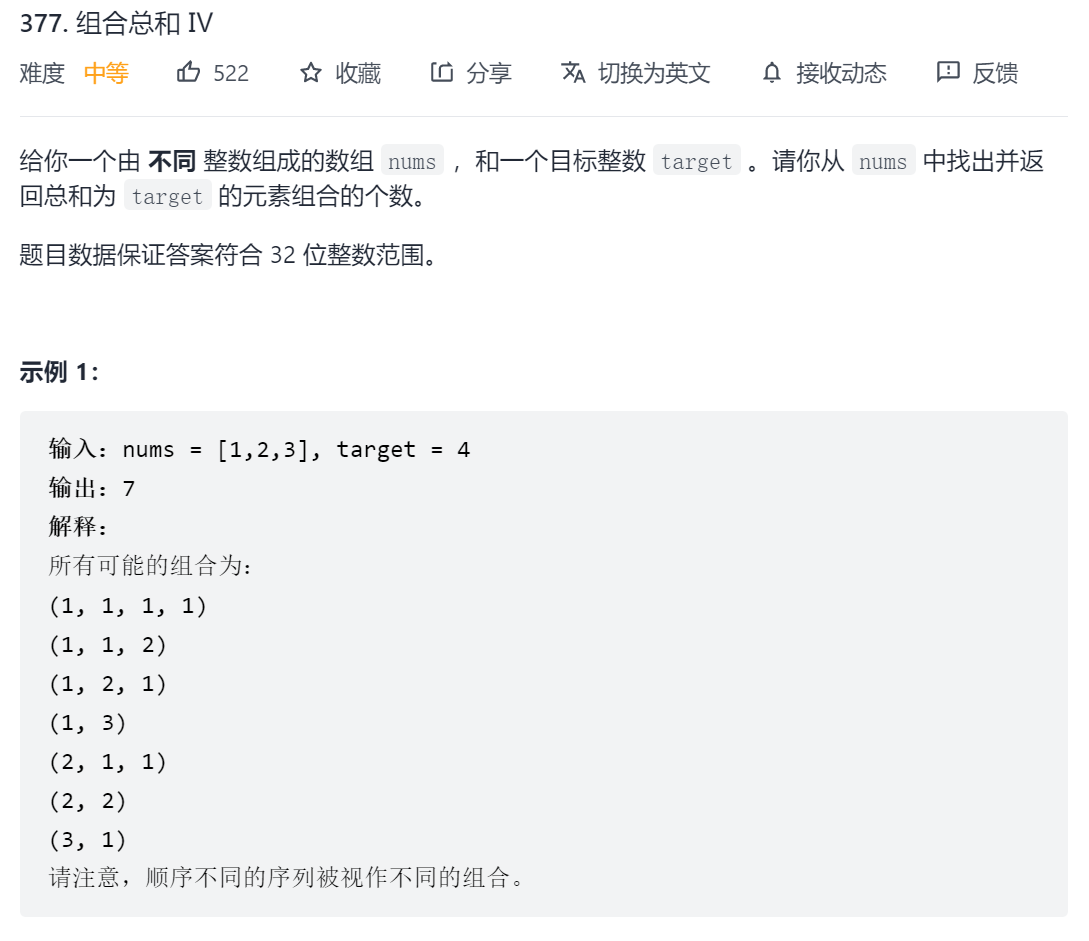

题目说的组合总和,因为不同顺序的序列为不同组合,所以实际上要找的是排列总和,因为每个数字可以选无限次,因此这是一个完全背包问题
因为题目没有要求把所有的排列都列出来,因此可以使用动态规划,否则只能回溯法暴力解决。
记和为j的组合数为个,我们不考虑这个组合具体是怎么组合的,每次新加一个数字
,直接将它放置于和为
的组合末尾,那么可以知道,
等于多少,那么
就会增加多少,因此状态转移方程为:
因为这是个完全背包问题,所以需要正向遍历背包容量,又因为这是一个排列问题,所以需要外层循环遍历背包容量,内层循环遍历物品
举个例子:如果外层循环遍历数字(物品),假如nums[0] = 1, nums[1] = 2,先加入1到组合中,再加入二到组合中,只会出现{1, 2}这种情况,不会出现{2, 1}。
而对于组合问题来说,内外层循环谁先谁后是都可以的
初始化dp[0]为1,表示和为0的组合有一种,表示什么都不选
class Solution {
public:
int combinationSum4(vector<int>& nums, int target) {
vector<int> dp(target + 1, 0);
dp[0] = 1;
for (int i = 0; i <= target; ++i) { // 排列问题,先遍历背包容量,在遍历物品
for (auto num : nums) {
if (i >= num && dp[i] < INT_MAX - dp[i - num])
dp[i] += dp[i - num];
}
}
return dp[target];
}
};
C++测试用例有超过两个数相加超过int的数据,所以需要在if里加上dp[i] < INT_MAX - dp[i - num]。
但java就不用考虑这个限制,java里的int也是四个字节吧,也有可能leetcode后台对不同语言的测试数据不一样。
总结:
如果求组合数就是外层for循环遍历物品,内层for遍历背包。
如果求排列数就是外层for遍历背包,内层for循环遍历物品。
70. 爬楼梯(进阶版)
在动规基础问题,讨论过爬楼梯这个问题,每次爬一节或者两节,爬到顶楼有几种方法,这是一个简单的动态规划问题。
现在修改一下题目,每次可以爬 1, 2,3,… ,m节楼梯,那么问题就转换为完全背包问题,爬楼节数视作物品,一次爬几节可以选择无数次,到顶楼是背包容量,那么这个问题就和377题求排列总数一样了。
class Solution {
public:
int climbStairs(int n) {
vector<int> dp(n + 1, 0);
dp[0] = 1;
for (int i = 1; i <= n; i++) { // 遍历背包
for (int j = 1; j <= m; j++) { // 遍历物品
if (i - j >= 0) dp[i] += dp[i - j];
}
}
return dp[n];
}
};
代码中m表示最多可以爬m个台阶,代码中把m改成2就是本题70.爬楼梯可以AC的代码了。
322. 零钱兑换
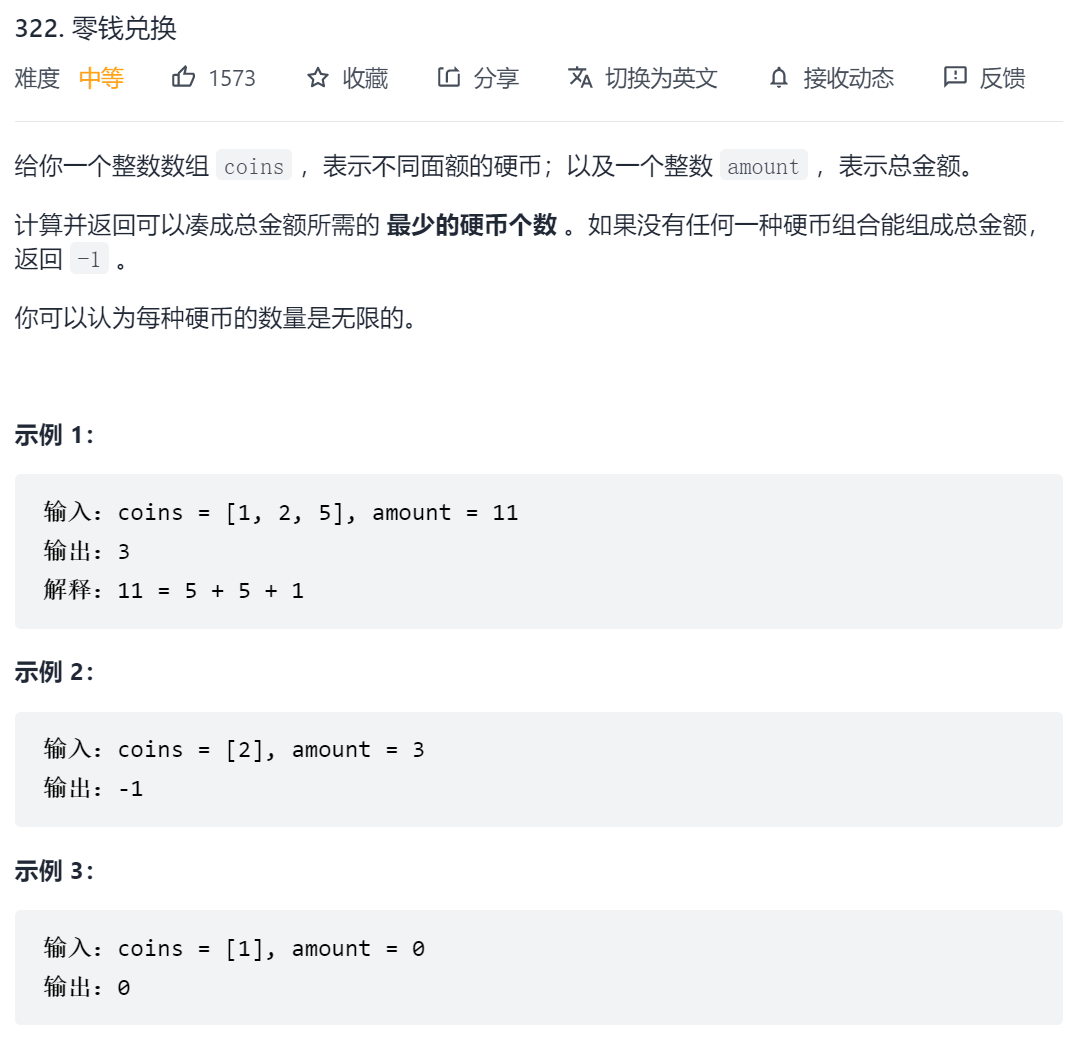
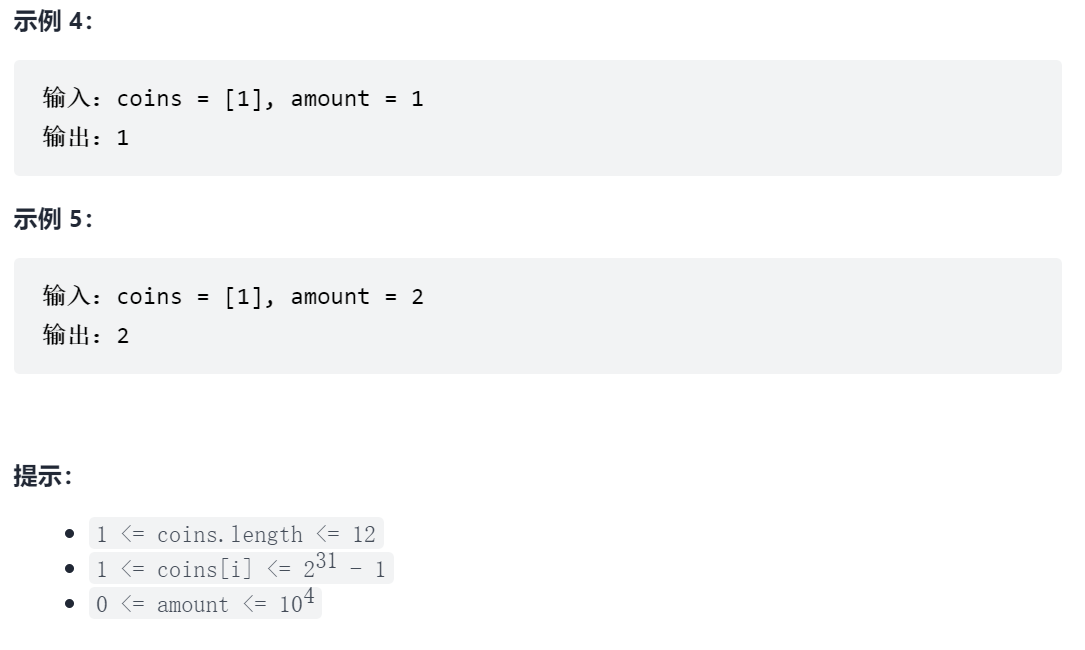
回溯法(待做)
动态规划
这是一个完全背包问题,自下而上思考,假设
为金额为i时需要的最少硬币数量,假设在考虑
的时候,已经解决了
,那么会有:
其中
是各种硬币面额,因为总金额为0时,需要的硬币数量为0, 因此
,
:凑足总额为j所需钱币的最少个数为
凑出金额 j 有两种情况:
- 不使用当前硬币就能凑出来dp[j],
此时dp[j]是未更新前的数据
- 使用当前硬币,
而题目要求能凑出 j 的最小值,因此状态转移方程:也得是所有
中的最小值,这实际上也是组合问题,求的是组合个数的最小值,不考虑钱币的顺序,因此遍历顺序都可
初始dp[0] = 0, 其余的都初始化为一个很大的数
例子: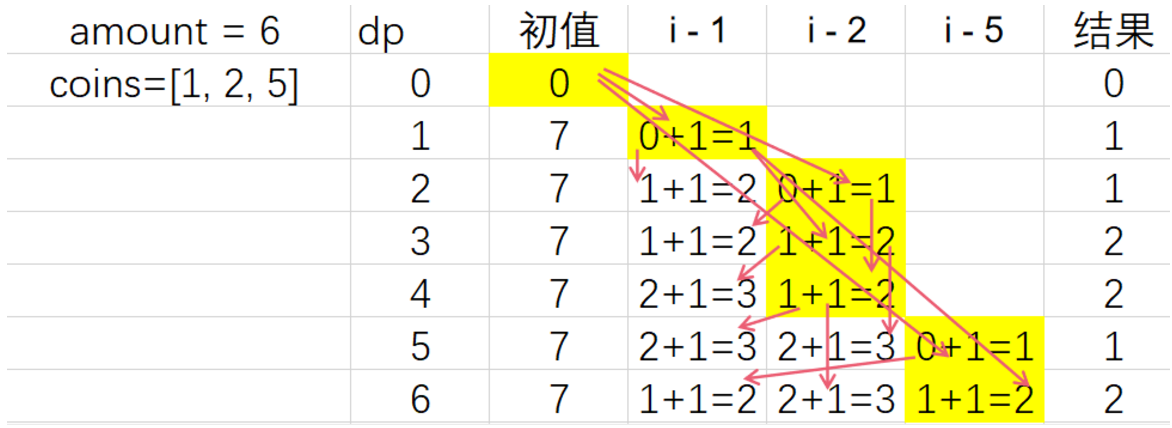
class Solution {
public:
int coinChange(vector<int>& coins, int amount) {
if (coins.empty()) return -1;
int Max = amount + 2;
vector<int> dp(amount + 1, Max);
dp[0] = 0;
for (int i = 1; i <= amount; ++i) {
for (const auto & coin : coins) {
if (i >= coin) {
dp[i] = min(dp[i], dp[i - coin] + 1);
}
}
}
return dp[amount] > amount ? -1 : dp[amount]; // 如果遍历以后dp[amount]仍是预订的值,说明不存在
}
};
int coinChange(vector<int>& coins, int amount) {
if (coins.empty()) return -1;
vector<int> dp(amount + 1, amount + 2);
dp[0] = 0;
for (int i = 1; i <= amount; ++i) {
for (const int & coin : coins) {
if (i >= coin) {
dp[i] = min(dp[i], dp[i-coin] + 1);
}
}
}
return dp[amount] == amount + 2? -1: dp[amount];
}
先遍历硬币,后遍历金额的版本
class Solution {
public:
int coinChange(vector<int>& coins, int amount) {
vector<int> dp(amount + 1, INT32_MAX);
dp[0] = 0;
for (auto coin : coins)
for (int i = 1; i <= amount; ++i)
if (i >= coin && dp[i - coin] != INT32_MAX) // 如果dp[i - coin]还没更新,就跳过,以免越界
dp[i] = min(dp[i - coin] + 1, dp[i]);
return dp[amount] > amount ? -1 : dp[amount]; // 如果dp[amount]还是原来的值,那么返回-1
}
};
279. 完全平方数

和硬币问题其实一样的,一个数的平方是硬币面额,n是总金额,求组成n使用硬币的最小数量
先遍历背包,再遍历物品
class Solution {
public:
int numSquares(int n) {
vector<int> dp(n + 1, INT_MAX);
dp[0] = 0;
for (int i = 1; i <= n; i++) { // 遍历背包
for (int j = 1; j * j <= i; j++) { //遍历物品
dp[i] = min(dp[i], dp[i - j * j] + 1); // 从不同的拆分方案里取最小值
}
}
return dp[n];
}
};
先遍历物品,再遍历背包
class Solution {
public:
int numSquares(int n) {
vector<int> dp(n + 1, INT_MAX);
dp[0] = 0;
for (int i = 1; i * i <= n; i++) { // 遍历物品
for (int j = 1; j <= n; j++) { // 遍历背包
if (j - i * i >= 0) {
dp[j] = min(dp[j - i * i] + 1, dp[j]);
}
}
}
return dp[n];
}
};
139. 单词拆分


用回溯法枚举字符串拆分的所有情况会超时(因为递归过程会有很多重复计算),使用记忆化递归可以不超时
class Solution {
private:
bool backtracking (const string& s,
const unordered_set<string>& wordSet,
vector<int>& memory,
int startIndex) {
if (startIndex >= s.size()) {
return true;
}
// 如果memory[startIndex]不是初始值了,直接使用memory[startIndex]的结果
if (memory[startIndex] != -1) return memory[startIndex];
for (int i = startIndex; i < s.size(); i++) {
string word = s.substr(startIndex, i - startIndex + 1);
if (wordSet.find(word) != wordSet.end() && backtracking(s, wordSet, memory, i + 1)) {
memory[startIndex] = 1; // 记录以startIndex开始的子串是可以被拆分的
return true;
}
}
memory[startIndex] = 0; // 记录以startIndex开始的子串是不可以被拆分的
return false;
}
public:
bool wordBreak(string s, vector<string>& wordDict) {
unordered_set<string> wordSet(wordDict.begin(), wordDict.end());
vector<int> memory(s.size(), -1); // -1 表示初始化状态
return backtracking(s, wordSet, memory, 0);
}
};
时间复杂度为O(2^n)
此题的最佳解法是用背包
把字符串s看作背包,把单词看作物品,每个单词可以取无限次,那么问题就转化为完全背包问题
记dp[i]表示[0, i)子串可以拆分成一个或者多个单词,值为布尔型,那么状态转移方程:dp[i] = dp[j] && isWord(j, i),意思是将[0, i) 分为两部分, [0,j),[j, i) dp[j] = true,并且[j, i)是一个单词,dp[i] = true
初始dp[0] = 0,表示空字符串能够拆分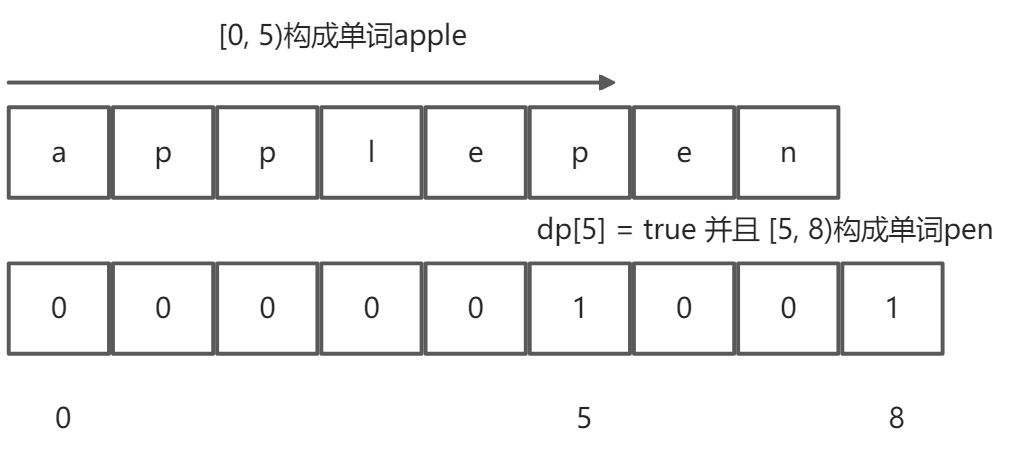
class Solution {
public:
bool wordBreak(string s, vector<string>& wordDict) {
unordered_set<string> wordSet(wordDict.begin(), wordDict.end());
vector<bool> dp(s.size() + 1, false);
dp[0] = true;
for (int i = 1; i <= s.size(); i++) {
for (int j = 0; j < i; j++) { // 将[0, i) 分为两部分, [0,j),[j, i) dp[j] = true,并且[j, i)是一个单词,dp[i] = true
string word = s.substr(j, i-j);//arg:起始位置,len
if (wordSet.find(word) != wordSet.end() && dp[j])
dp[i] = true;
}
}
return dp[s.size()];
}
};
或者用处理完全平方数的思路,状态转移方程为dp[i] = dp[i] || dp[i - len],当i > 某个单词长度时,如果[i - len, i)是这个单词,那么如果dp[i]已经是true,能拆,或者dp[i - len]是true的时候,dp[i]都为true
class Solution {
public:
bool wordBreak(string s, vector<string>& wordDict) {
int n = s.length();
vector<bool> dp(n + 1, false);
dp[0] = true;
for (int i = 1; i <= n; ++i) { // 遍历背包容量
for (const string & word: wordDict) { // 遍历物品
int len = word.length();
// 如果长度为word.size()的子串刚好是word,那么更新dp
if (i >= len && s.substr(i - len, len) == word) {
dp[i] = dp[i] || dp[i - len];
}
}
}
return dp[n];
}
};



