顺序表（数组）

数组理论基础

数组在内存中的存储方式:
数组是存放在连续内存空间上的相同类型数据的集合。

数组可以方便的通过下标索引的方式获取到下标下对应的数据。

举一个字符数组的例子，如图所示：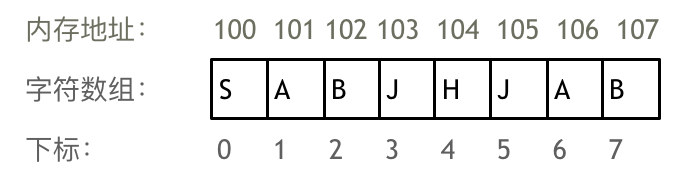
线性表 - 图1
需要两点注意的是

  • 数组下标都是从0开始的。
  • 数组内存空间的地址是连续的

正是因为数组的在内存空间的地址是连续的，所以我们在删除或者增添元素的时候，就难免要移动其他元素的地址。
例如删除下标为3的元素，需要对下标为3的元素后面的所有元素都要做移动操作，如图所示：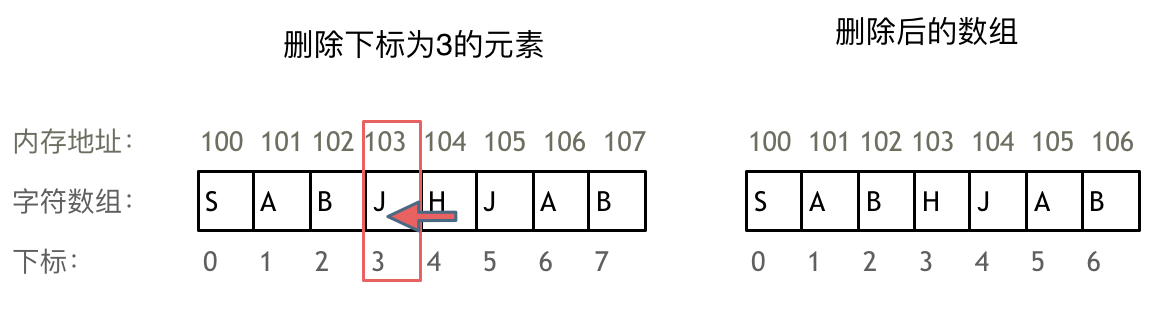
线性表 - 图2
而且大家如果使用C++的话，要注意vector 和 array的区别，vector的底层实现是array，严格来讲vector是容器，不是数组。
数组的元素是不能删的，只能覆盖。
那么二维数组直接上图，大家应该就知道怎么回事了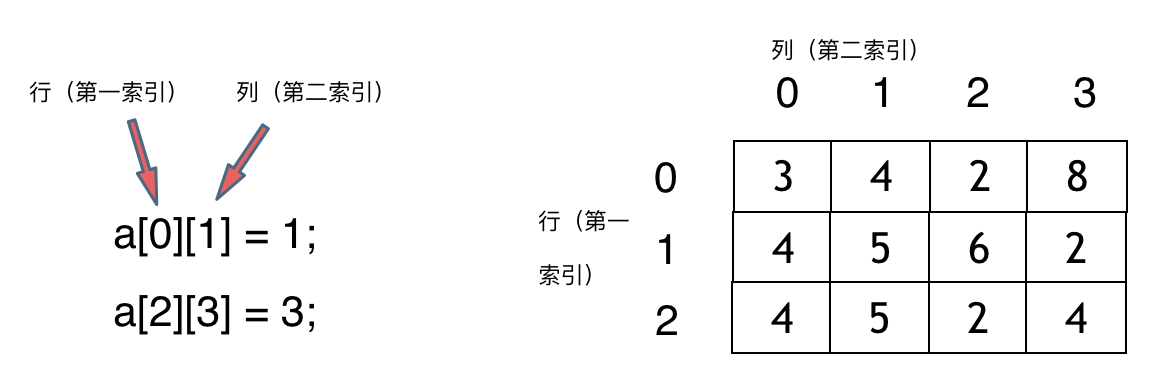
线性表 - 图3
那么二维数组在内存的空间地址是连续的么？
我们来举一个例子，例如： int[][] rating = new int[3][4]; ， 这个二维数据在内存空间可不是一个 34 的连续地址空间
看了下图，就应该明白了：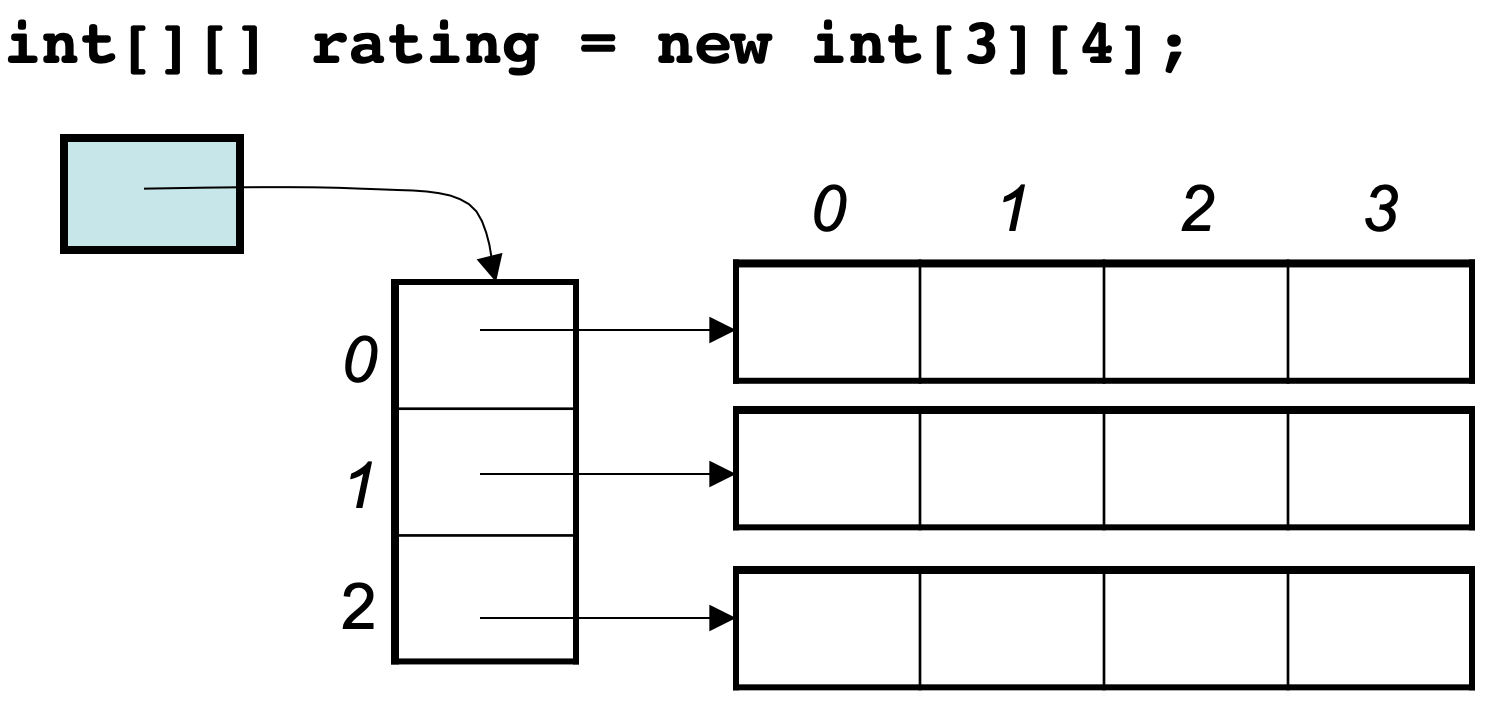
线性表 - 图4
所以**二维数据在内存中不是 34 的连续地址空间，而是四条连续的地址空间组成！**

链表

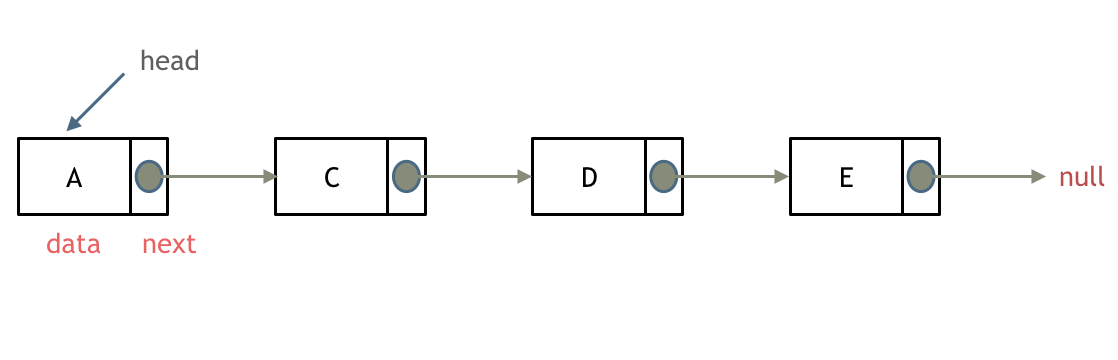
链表是一种通过指针串联在一起的线性结构，每一个节点是又两部分组成，一个是数据域一个是指针域（存放指向下一个节点的指针），最后一个节点的指针域指向null（空指针的意思）。
链接的入口点称为列表的头结点也就是head。
如图所示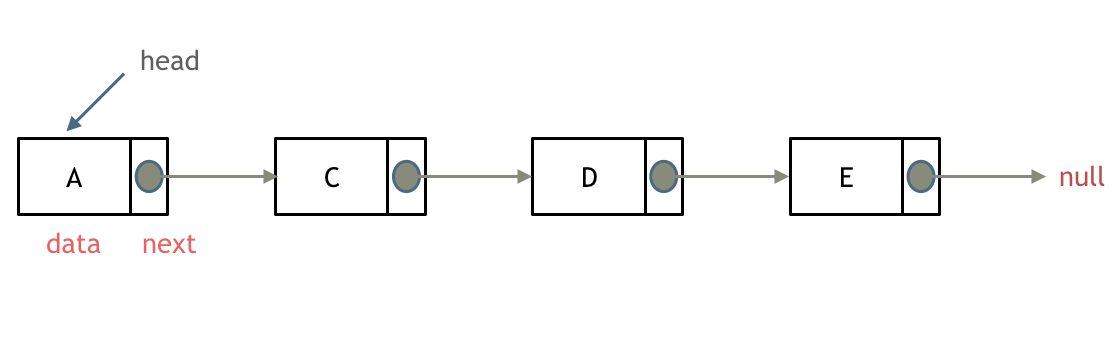： image.png

链表的类型

单链表

单链表中的节点只能指向节点的下一个节点。
image.png

双链表

双链表：每一个节点有两个指针域，一个指向下一个节点，一个指向上一个节点。
双链表 既可以向前查询也可以向后查询。
如图所示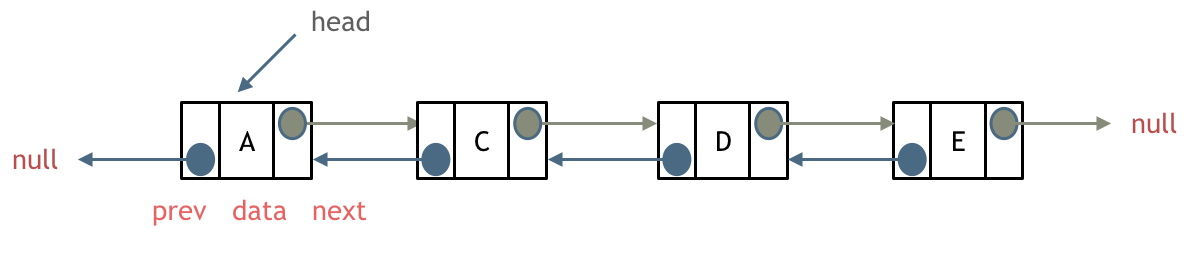： image.png

循环链表

循环链表，顾名思义，就是链表首尾相连。
循环链表可以用来解决约瑟夫环问题。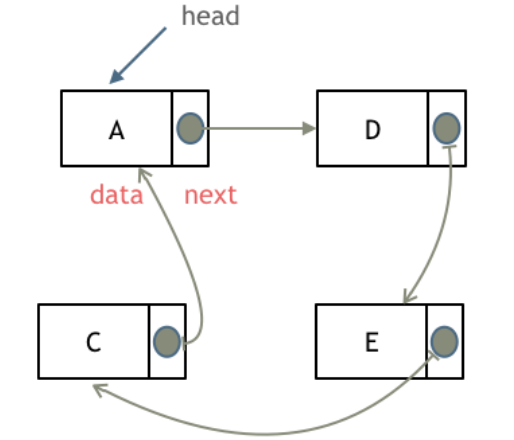
image.png

链表的存储方式

数组是在内存中是连续分布的，但是链表在内存中可不是连续分布的。
链表是通过指针域的指针链接在内存中各个节点。
所以链表中的节点在内存中不是连续分布的 ，而是散乱分布在内存中的某地址上，分配机制取决于操作系统的内存管理。
如图所示：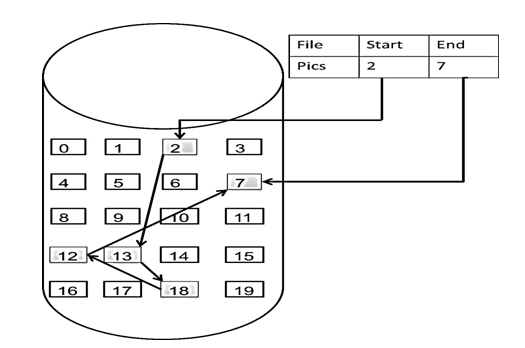
image.png
这个链表起始节点为2， 终止节点为7， 各个节点分布在内存个不同地址空间上，通过指针串联在一起。

链表的定义

  1. // 单链表
  2. struct ListNode {
  3.     int val;  // 节点上存储的元素
  4.     ListNode *next;  // 指向下一个节点的指针
  5.     ListNode(int x) : val(x), next(NULL) {}  // 节点的构造函数
  6. };

通过自己定义构造函数初始化节点：

ListNode* head = new ListNode(5);

使用默认构造函数初始化节点：

ListNode* head = new ListNode();
head->val = 5;

所以如果不定义构造函数使用默认构造函数的话，在初始化的时候就不能直接给变量赋值！

链表的操作

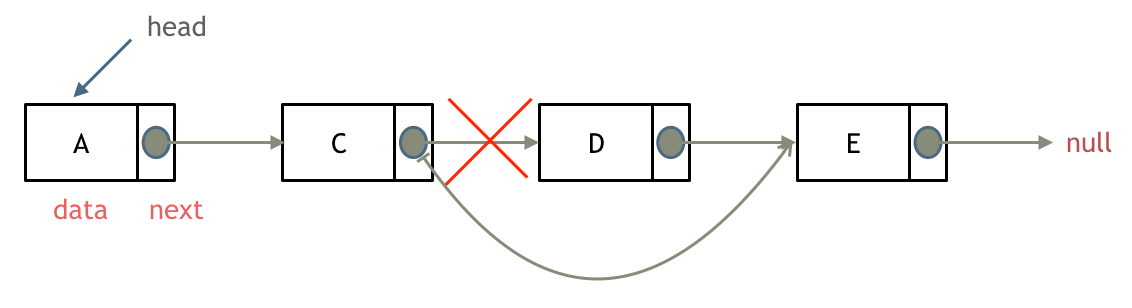
删除节点

删除D节点，如图所示：
image.png

添加节点

如图所示：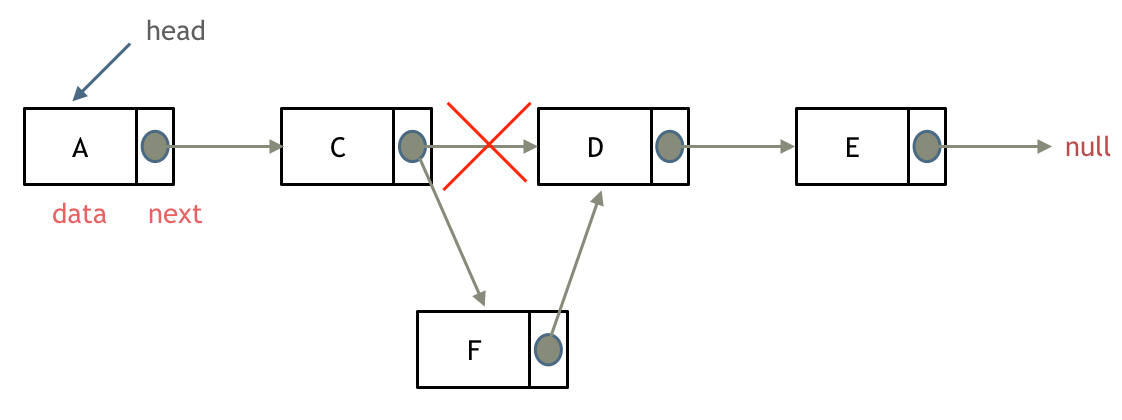
image.png
可以看出链表的增添和删除都是O(1)操作，也不会影响到其他节点。
但是要注意，要是删除第五个节点，需要从头节点查找到第四个节点通过next指针进行删除操作，查找的时间复杂度是O(n)。

性能分析

再把链表的特性和数组的特性进行一个对比，如图所示：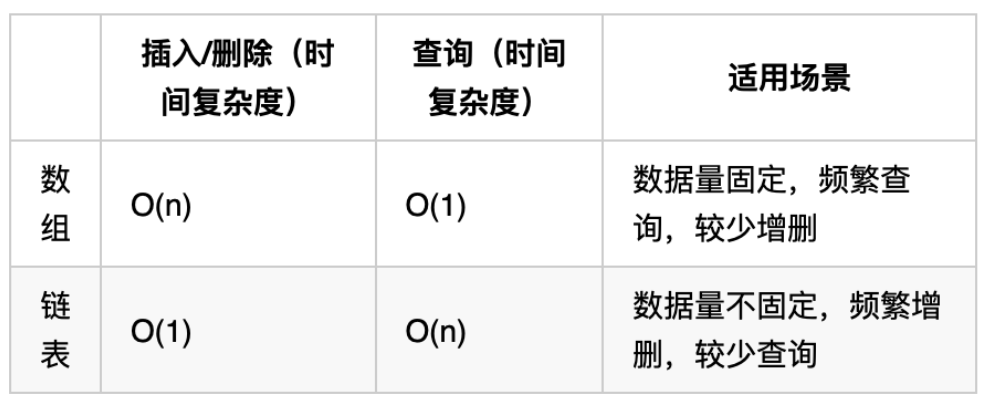
image.png
数组在定义的时候，长度就是固定的，如果想改动数组的长度，就需要重新定义一个新的数组。
链表的长度可以是不固定的，并且可以动态增删， 适合数据量不固定，频繁增删，较少查询的场景。

完整代码

#include <iostream>

using namespace std;

class Node
{
public:
    Node()
    {
        data = 0;
        next = NULL;
    }
    Node(int n) : data(n), next(NULL){};

public:
    int data;
    Node *next;
};

//含有头结点的单链表
class LinkList
{
public:
    //构造一个空链表，有头结点
    LinkList()
    {
        Node *q = new Node;
        head = q; //头指针指向头结点
    };

    //尾插法
    void addItemTail(int n)
    {
        Node *q = new Node(n);
        Node *p = head;
        while (p->next != NULL)
            p = p->next;
        p->next = q;
    }

    //头插法
    void addItemHead(int n)
    {
        Node *q = new Node(n);
        q->next = head->next;
        head->next = q;
    }

    //删除索引为i的节点
    void deleteItem(int index)
    {
        if (!head->next)
        {
            cout << "链表为空" << endl;
            return;
        }

        int i = 0;
        Node *p = head;

        while (i < index && p->next)
        {
            p = p->next;
            ++i;
        }
        if (i == index && p->next) {//处理下标越界
            Node *q = p->next;
            p->next = q->next;
            delete q;
        }
        else
        {
            cout << "索引错误" << endl;
        }

    }

    void output()
    {
        Node *p = head->next;
        while (p != NULL)
        {
            cout << p->data << " ";
            p = p->next;
        }
        cout << endl;
    }

public:
    Node *head;//头指针
};

void test01()
{
    LinkList list;
    for (int i = 0; i < 6; ++i)
    {
        list.addItemHead(i);
    }
    list.output();
    list.deleteItem(6);
    list.output();
}

void test02()
{
    LinkList list;
    list.deleteItem(1);
}

int main()
{
    test01();
    return 0;
}