59. 螺旋矩阵 II

这道题思路不难,但是容易写错
思路:由外向内逐圈给res赋值,用(x1,y1) 和 (x1, y2)分别定位每一圈的左上角和右下角,然后循环输出即可
class Solution {public:vector<vector<int>> generateMatrix(int n) {vector<vector<int>> res(n, vector<int>(n));int x1 = 0, y1 = 0, x2 = n - 1, y2 = n - 1; //记录左上角和右下角的坐标int num = 1;while (x1 <= x2 && y1 <= y2) {int posX = x1, posY = y1;//上面一行while (posY <= y2) res[posX][posY++] = num++;//右边一列posY = y2;posX++;while (posX <= x2) res[posX++][posY] = num++;//下边一列posX = x2;posY--;while (posY >= y1) res[posX][posY--] = num++;//左边一列posY = y1;posX--;while (posX > x1) res[posX--][posY] = num++;x1++;y1++;x2--;y2--;}return res;}};
矩阵通用模板
注意++i 和 —i 别写错了
class Solution {
public:
vector<vector<int>> generateMatrix(int n) {
vector<vector<int>> res(n, vector<int>(n, 0));
int x1 = 0, y1 = 0; // 左上角
int x2 = n - 1, y2 = n - 1; // 右下角
int num = 1;
while (x1 <= x2 && y1 <= y2) {
for (int i = y1; i <= y2; ++i) {
res[x1][i] = num++;
}
for (int i = x1 + 1; i <= x2; ++i) {
res[i][y2] = num++;
}
if (x1 < x2 && y1 < y2) {
for (int i = y2 - 1; i >= y1; --i) {
res[x2][i] = num++;
}
for (int i = x2 - 1; i >= x1 + 1; --i) {
res[i][x1] = num++;
}
}
++x1;
++y1;
--x2;
--y2;
}
return res;
}
};
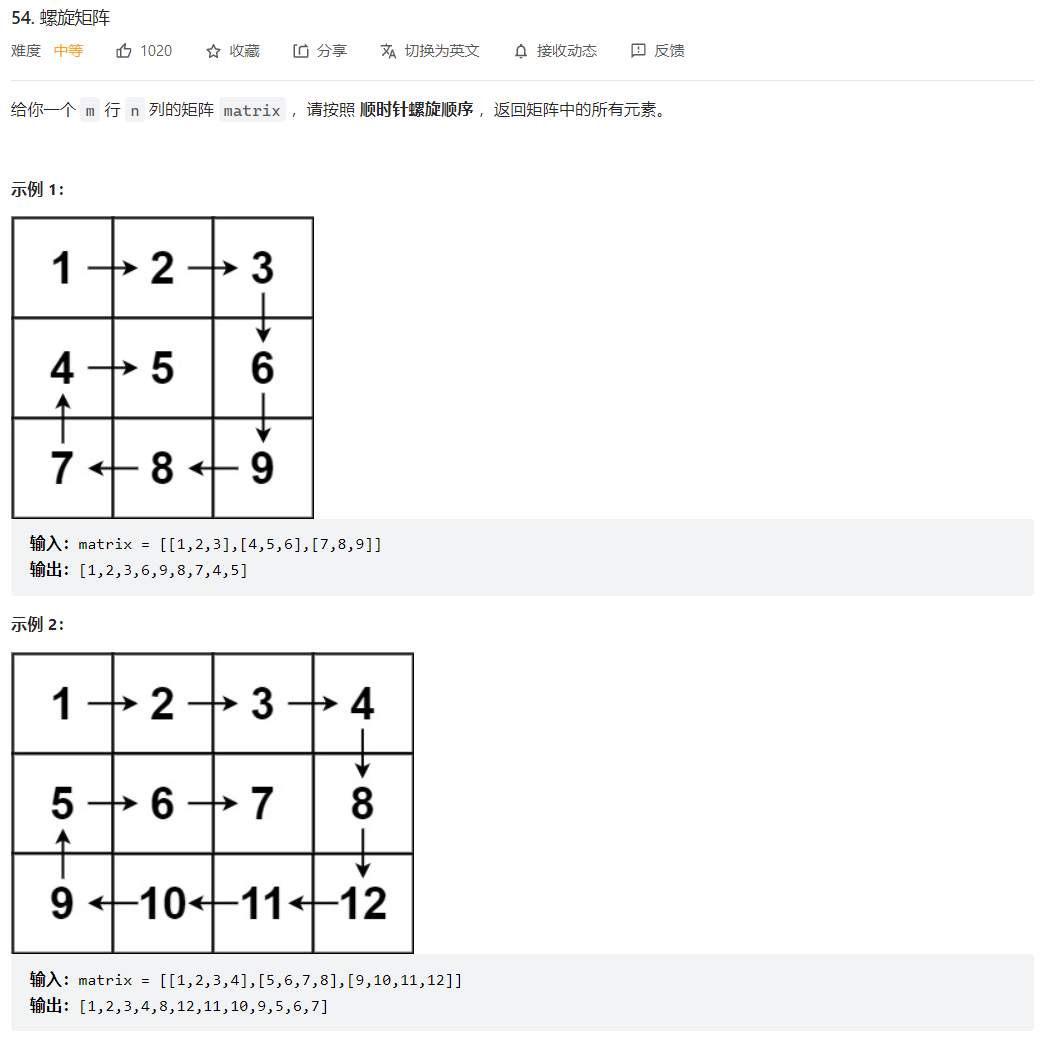
54. 螺旋矩阵
阵
这道题和59不一样的地方在于要输出的矩阵不是方阵,因此要考虑的边界问题会更多
思路一
分层遍历,一圈一圈的处理矩阵,最后再处理不成环的情况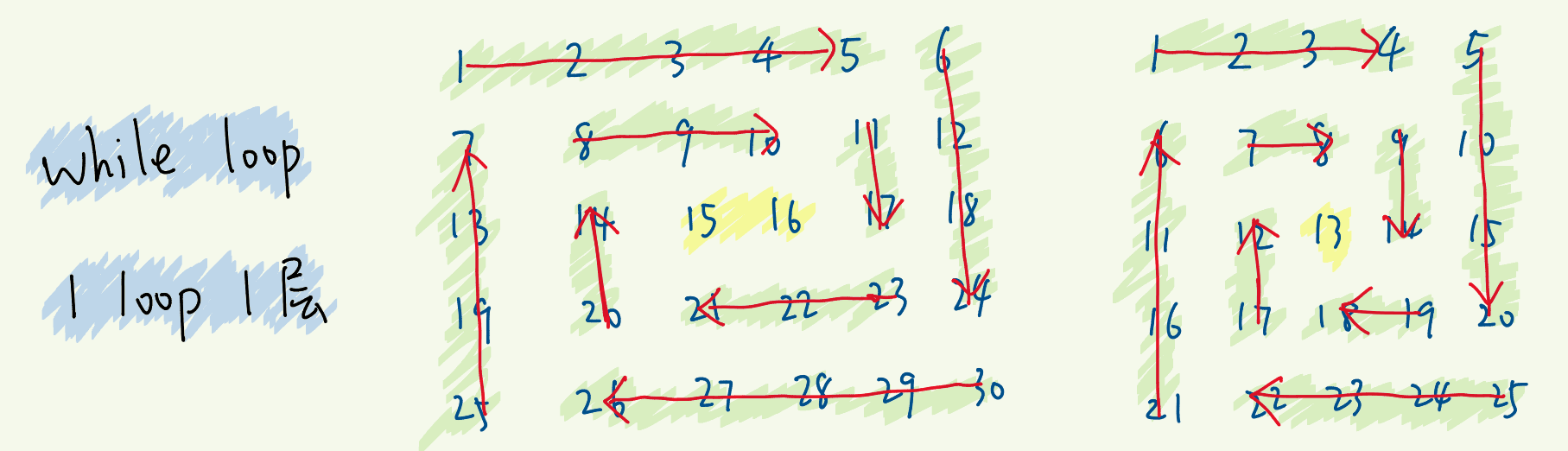
- 如果一条边从头遍历到底,则下一条边遍历的起点随之变化
- 选择不遍历到底,可以减小横向、竖向遍历之间的影响
- 一轮迭代结束时,4条边的两端同时收窄 1
- 一轮迭代所做的事情变得很清晰:遍历一个“圈”,遍历的范围收缩为内圈
- 一层层向里处理,按顺时针依次遍历:上、右、下、左。
- 不再形成“环”了,就会剩下一行或一列,然后单独判断
四个边界
上边界 top : 0
下边界 bottom : matrix.length - 1
左边界 left : 0
右边界 right : matrix[0].length - 1
矩阵不一定是方阵
top < bottom && left < right 是循环的条件
无法构成“环”了,就退出循环,退出时可能是这 3 种情况之一:
top == bottom && left < right —— 剩一行
top < bottom && left == right —— 剩一列
top == bottom && left == right —— 剩一项(也是一行/列)
处理剩下的单行或单列
因为是按顺时针推入结果数组的,所以
剩下的一行,从左至右 依次推入结果数组
剩下的一列,从上至下 依次推入结果数组
代码
每个元素访问一次,时间复杂度 O(mn),m、n 分别是矩阵的行数和列数
空间复杂度 O(mn)
Runtime: 0 ms, faster than 100.00% of Go online submissions for Spiral Matrix.
class Solution {
public:
vector<int> spiralOrder(vector<vector<int>>& matrix) {
int m = matrix.size(), n = matrix[0].size();
vector<int> res;
int x1 = 0, y1 = 0, x2 = m - 1, y2 = n - 1; //定位左上角和右下角
while(x1 < x2 && y1 < y2) {
//上
for (int i = y1; i < y2; ++i) res.push_back(matrix[x1][i]);
//右
for (int i = x1; i < x2; ++i) res.push_back(matrix[i][y2]);
//下
for (int i = y2; i > y1; --i) res.push_back(matrix[x2][i]);
//左
for (int i = x2; i > x1; --i) res.push_back(matrix[i][y1]);
//收缩
x1++;
y1++;
x2--;
y2--;
}
if (x1 == x2)//剩下一行
for(int i = y1; i <= y2; ++i) res.push_back(matrix[x1][i]);
else if (y1 == y2)//剩下一列
for(int i = x1; i <= x2; ++i) res.push_back(matrix[i][y1]);
return res;
}
};
思路二
遍历到底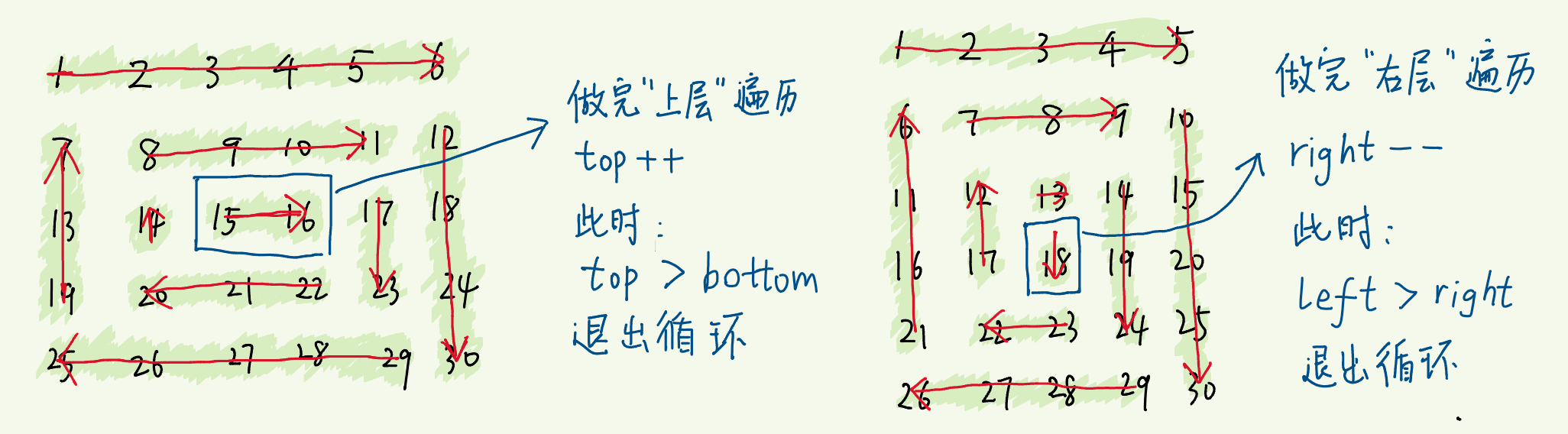
- 循环的条件改为: top <= bottom && left <= right
- 每遍历一条边,下一条边遍历的起点被“挤占”,要更新相应的边界
- 需注意到,可能在循环途中,突然不再满足循环的条件,即top > bottom或left > right,其中一对边界彼此交错了
- 这意味着所有项都遍历完了,要break了,如果没有及时 break ,就会重复遍历
解决办法
- 每遍历完一条边,更新相应的边界后,都加上一句if (top > bottom || left > right) break;,避免没有及时退出循环,导致重复遍历。
- 而且,遍历完成这个时间点,要么发生在遍历完“上边”,要么发生在遍历完“右边”
所以只需在这两步操作之后,加 if (top > bottom || left > right) break 即可
class Solution { public: vector<int> spiralOrder(vector<vector<int>>& matrix) { int m = matrix.size(), n = matrix[0].size(); vector<int> res; int x1 = 0, y1 = 0, x2 = m - 1, y2 = n - 1; //定位左上角和右下角 while(x1 <= x2 && y1 <= y2) { //上 for (int i = y1; i <= y2; ++i) res.push_back(matrix[x1][i]); x1++; //右 for (int i = x1; i <= x2; ++i) res.push_back(matrix[i][y2]); y2--; //避免重复遍历 if (x1 > x2 || y1 > y2) break; //下 for (int i = y2; i >= y1; --i) res.push_back(matrix[x2][i]); x2--; //左 for (int i = x2; i >= x1; --i) res.push_back(matrix[i][y1]); y1++; //收缩 } return res; } };
class Solution {
public:
vector<int> spiralOrder(vector<vector<int>>& matrix) {
vector<int> res;
int m = matrix.size(), n = matrix[0].size();
int x1 = 0, y1 = 0; // 左上角
int x2 = m - 1, y2 = n - 1; // 右下角
while (x1 <= x2 && y1 <= y2) {
for (int i = y1; i <= y2; ++i) {
res.push_back(matrix[x1][i]);
}
for (int i = x1 + 1; i <= x2; ++i) {
res.push_back(matrix[i][y2]);
}
if (x1 < x2 && y1 < y2) { // 防止重复打印
for (int i = y2 - 1; i >= y1; --i) {
res.push_back(matrix[x2][i]);
}
for (int i = x2 - 1; i >= x1 + 1; --i) {
res.push_back(matrix[i][x1]);
}
}
++x1;
++y1;
--x2;
--y2;
}
return res;
}
};
88. 合并两个有序数组
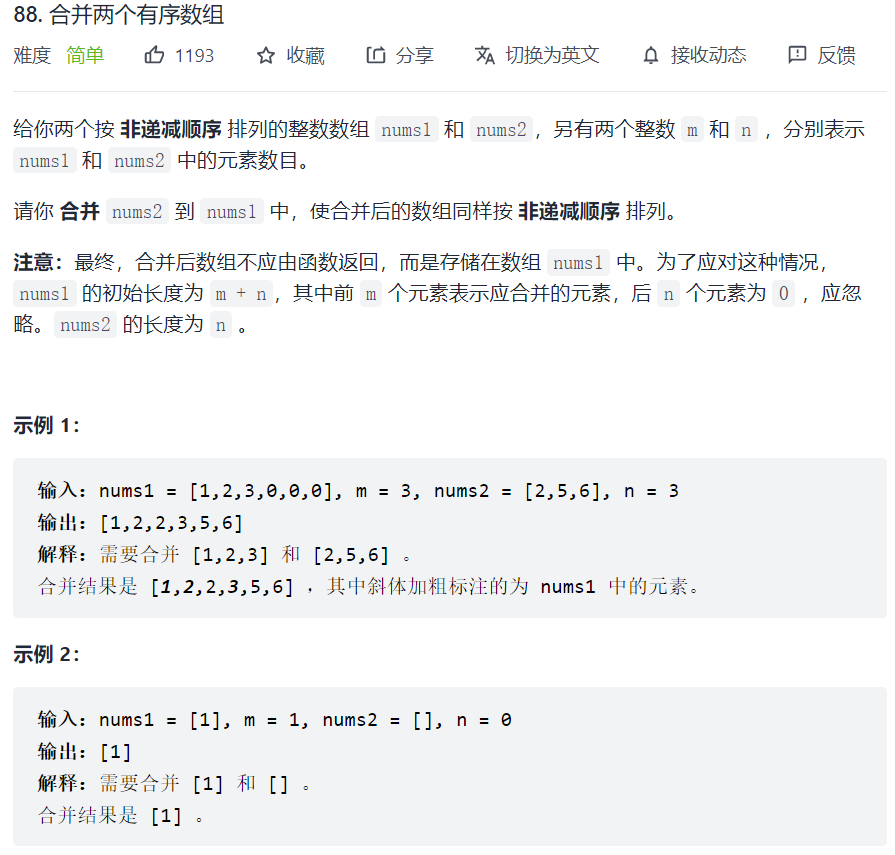
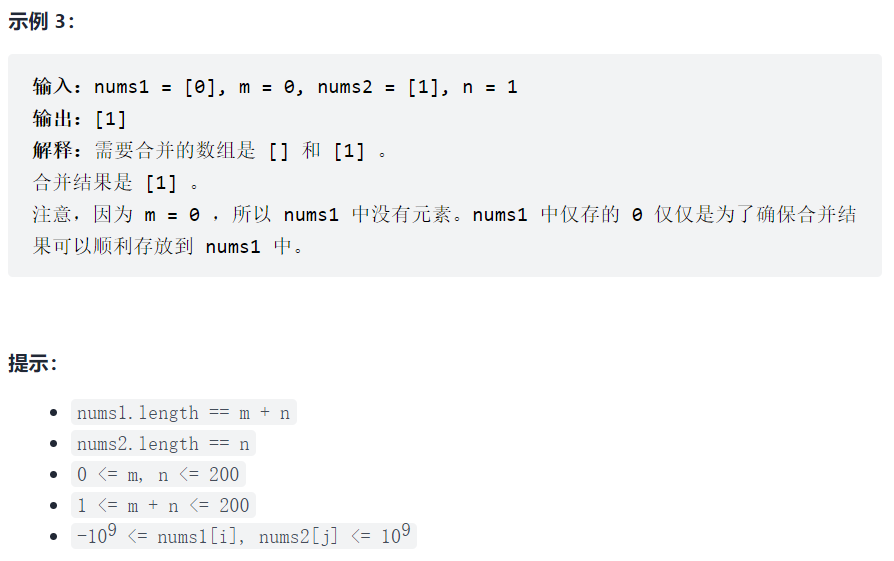
LeetCode 88 题
- 解法1:直接将数组2插入到数组1后面,然后对合并后的数组进行排序
class Solution {
public:
void merge(vector<int>& nums1, int m, vector<int>& nums2, int n) {
for (int i = 0; i < nums2.size(); ++i) {
nums1[m + i] = nums2[i];
}
sort(nums1.begin(), nums1.end());
}
};
- 解法二:双指针
因为初始数组是有序的,因此用两个指针来遍历两个数组,每次取最小的
class Solution {
public:
void merge(vector<int>& nums1, int m, vector<int>& nums2, int n) {
int p1 = 0, p2 = 0;
int sorted[m + n]; //用于保留合并后的数组 空间复杂度 O(m+n)
int cur;
while (p1 < m || p2 < n) {
if (p1 == m) {
cur = nums2[p2++];
} else if (p2 == n) {
cur = nums1[p1++];
} else if (nums1[p1] < nums2[p2]) {
cur = nums1[p1++];
} else {
cur = nums2[p2++];
}
sorted[p1 + p2 - 1] = cur;
}
for (int i = 0; i != m + n; ++i) {
nums1[i] = sorted[i];
}
}
};
- 解法3:逆向双指针
对于解法2,从头往后遍历数组的话,如果不用额外的数组,有些元素可能被覆盖,因为元素初始有序,且数组空间够大,可以使用逆向双指针,从后往前比较两个数组中较大者,放到nums1的后面,这样可以将nums1剩余的空间利用起来,不需要额外空间,空间复杂度为O(1)
class Solution {
public:
void merge(vector<int>& nums1, int m, vector<int>& nums2, int n) {
int p1 = m - 1, p2 = n - 1;
int index = m + n - 1;
while (p1 >= 0 && p2 >= 0) {
if (nums1[p1] >= nums2[p2]) {
nums1[index--] = nums1[p1--];
} else {
nums1[index--] = nums2[p2--];
}
}
// 如果nums1剩余元素未处理完,则不用处理
// 处理nums2
while (p2 >= 0) {
nums1[index--] = nums2[p2--];
}
}
};
645. 错误的集合

数组[1, 2, 2, 4]
索引 0, 1, 2, 3
i=0和i=1时,发现 nums[i] = i+1,也就是位置正确 while里的条件是false
i=2时,发现nums[i] != i+1,也就是说位置不对,
那么这个元素本来应该放的位置处的索引是index = 数值(nums[i]) - 1,因为正确的位置数值都会比索引大1
但是找到应在的位置,发现nums[index]处的值和nums[i]一样,也就是说这个元素有可能是被nums[nums[i] - 1]替换的,所以位置依然是“正确的”,所以while中的条件 nums[nums[i] - 1] != nums[i] 仍然是false
数组[2, 2, 4, 1]
索引 0, 1, 2, 3
nums[0] 不等于1,但是 nums[2-1]=nums[1]=nums[0]=2,所以暂时认为1被2替换,然后nums[1]等于2,跳过
//while
nums[2] 不等于 3并且nums[4-1]不等于4, 交换 nums[2]和nums[3],数组变为[2, 2, 1, 4],交换完发现nums[2]还是不等于3,并且nums[1-1]不等于1,接着交换,数组变为[1,2,2,4],
然后所有元素都在正确的位置了
class Solution {
public:
vector<int> findErrorNums(vector<int>& nums) {
for (int i = 0; i < nums.size(); i++)
{
while (nums[i] != i + 1 && nums[nums[i] - 1] != nums[i])
{
/* nums[i] != i + 1代表元素位置不对
nums[nums[i] - 1] != nums[i] 不是被替换的元素,
如果位置不对并且被其他元素替换了,就不用管它
每次 while 索引i处的值都会在正确的位置
如果输入是 [1,2,2,4]这种,这个循环没什么吊用
如果输入是[2,2,4,1]这种位置不对的,这个循环会把数组变为[1,2,2,4]
*/
swap_index(nums, i, nums[i] - 1);
}
}
for (int i = 0; i < nums.size(); i++)
{
//找到被覆盖的元素,那么重复的元素就是nums[i],被覆盖的就是 i+1
if (nums[i] != i + 1)
return vector<int>{nums[i], i + 1};
}
return vector<int>{};
}
void swap_index(vector<int> &nums, int i, int j)
{
int temp = nums[i];
nums[i] = nums[j];
nums[j] = temp;
}
};
2022.03.21版本
集合大小为n,元素为 1 ~ n,假设有一个数组存放这n个元素,将数组排序后,假设数组下标为1,应有
nums[i] = i + 1,成这个元素位于“正确”的位置
现在,题目给的数组是无序的,可以想办法将元素置于“正确”的位置:
循环遍历数组,对于每一个nums[i],都可以通过循环使nums[i] = i + 1,假如nums[i] != i + 1,设nums[i]= t , 那么尝试将其与nums[t - 1]处的元素交换,交换后,nums[t - 1] = t,一个元素找到“正确”的位置,每次循环都会有一个元素找到正确位置,因此,所有元素都处理完毕,时间复杂度为O(N),假如nums[t - 1] = t,说明 t重复,不必交换,这时候只知道重复的是哪个,缺失的是谁还不能判断,因此不能直接输出
for (int i = 0; i < nums.size(); ++i) {
while (nums[i] != i + 1 && nums[nums[i] - 1] != nums[i]) {
int temp = nums[i];
nums[i] = nums[nums[i] - 1];
nums[temp - 1] = temp;
}
}
数组处理完毕后,再遍历一次数组,如果nums[i] != i + 1,则重复元素为nums[i],缺失元素为 i + 1
for (int i = 0; i < nums.size(); ++i) {
if (nums[i] != i + 1) {
return {nums[i], i + 1};
}
}
完整代码:
class Solution {
public:
vector<int> findErrorNums(vector<int>& nums) {
for (int i = 0; i < nums.size(); ++i) {
while (nums[i] != i + 1 && nums[nums[i] - 1] != nums[i]) {
int temp = nums[i];
nums[i] = nums[nums[i] - 1];
nums[temp - 1] = temp;
}
}
for (int i = 0; i < nums.size(); ++i) {
if (nums[i] != i + 1) {
return {nums[i], i + 1};
}
}
return {};
}
};
(21.11.10每日一题)495. 提莫攻击
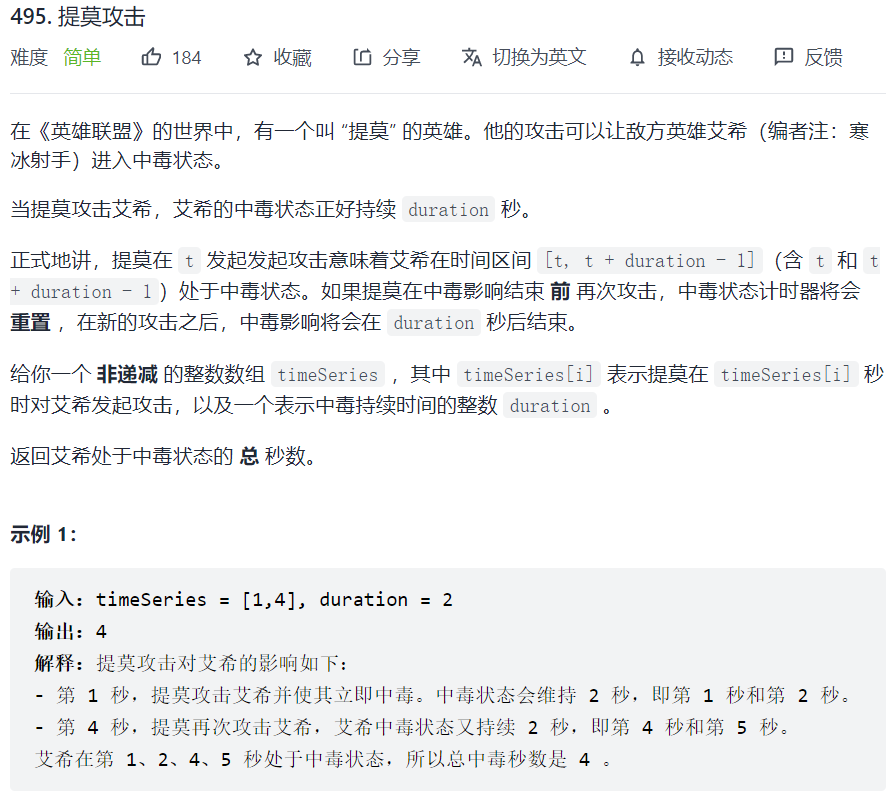

这是用数组模拟提莫的带毒攻击
考虑下面两种情况,始终:
timeSeries[i + 1] - timeSeries[i] <= duration:result += timeSeries[i + 1] - timeSeries[i]timeSeries[i + 1] - timeSeries[i] > duration:result += duration
完整代码:
class Solution {
public:
int findPoisonedDuration(vector<int>& timeSeries, int duration) {
if (timeSeries.size() == 0) return 0;
int result = 0;
int i = 0;
for (; i < timeSeries.size() - 1; i++) {
if (timeSeries[i + 1] - timeSeries[i] <= duration) {
result += timeSeries[i + 1] - timeSeries[i];
} else {
result += duration;
}
}
result += duration;
return result;
}
};
498. 对角线遍历
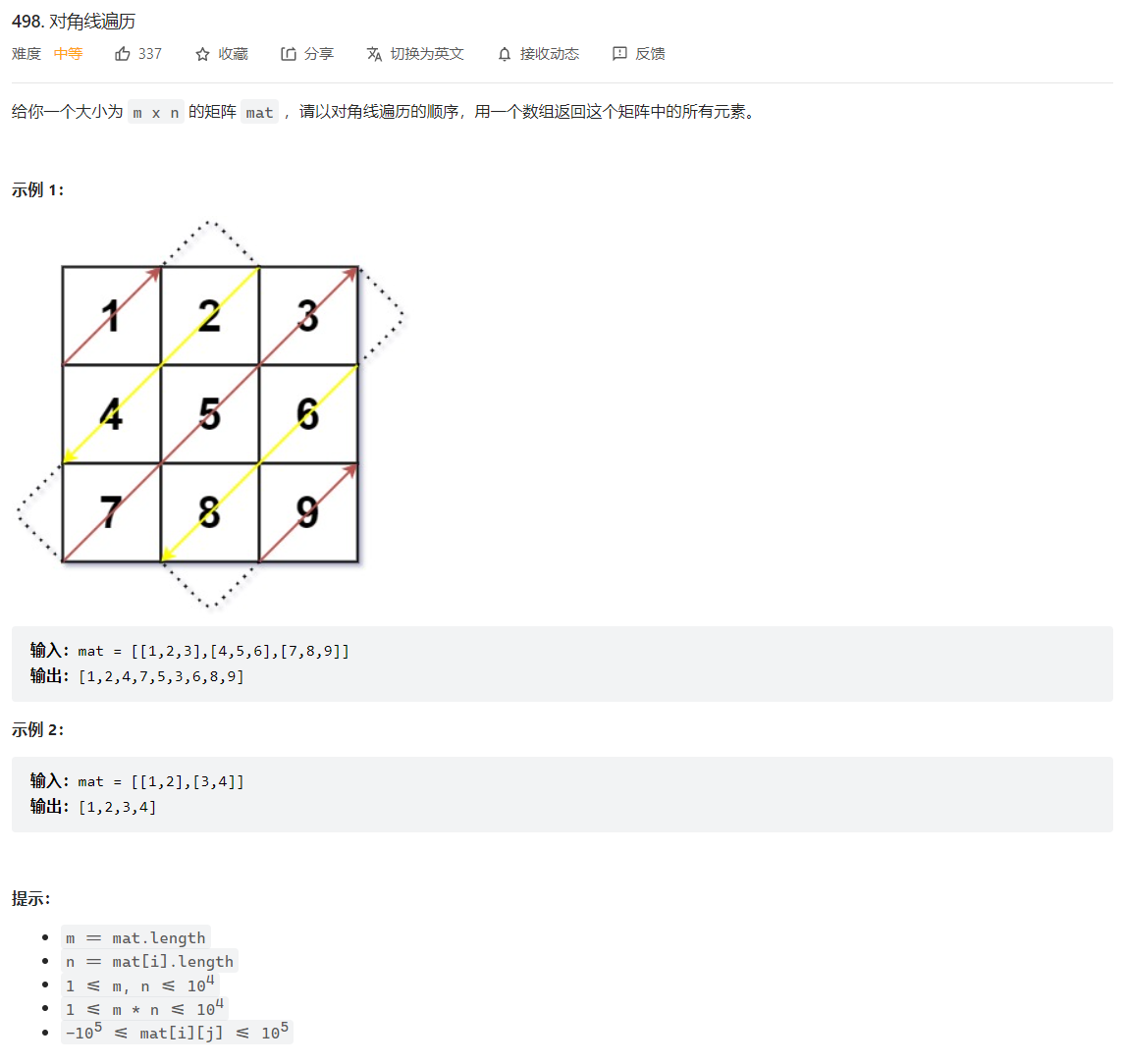
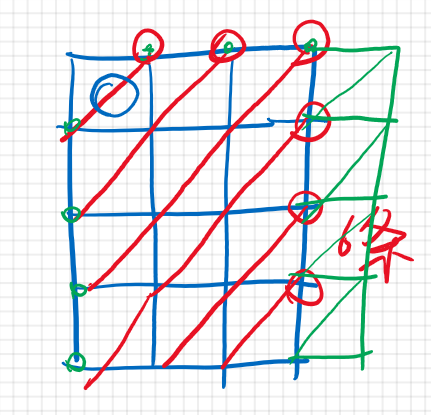
可以发现m行n列的矩阵一共有m + n - 1条对角线(数红点)
然后需要遍历m+n-1次
通过遍历次数的奇偶性区分遍历方向即可
class Solution {
public:
vector<int> findDiagonalOrder(vector<vector<int>>& mat) {
vector<int> res;
int m = mat.size(), n = mat[0].size();
int len = m + n - 1;
for (int k = 0; k < len; k++) {
if ((k & 1) == 0) { // 从下往上
int i = k < m ? k : m - 1; // 左上三角从k行开始遍历 右下三角从最后一行开始遍历
int j = k < m ? 0 : k - m + 1; // 左上三角从第一列开始遍历 右下三角从第 k - m + 1列开始
while (i >= 0 && j < n) {
res.push_back(mat[i][j]);
i--;
j++;
}
} else {
int i = k < n ? 0 : k - n + 1;
int j = k < n ? k : n - 1;
while (i < m && j >= 0) {
res.push_back(mat[i][j]);
i++;
j--;
}
}
}
return res;
}
};