- 剑指 Offer 10- I. 斐波那契数列">剑指 Offer 10- I. 斐波那契数列
- 剑指 Offer 10- II. 青蛙跳台阶问题">剑指 Offer 10- II. 青蛙跳台阶问题
- 剑指 Offer 14- I. 剪绳子">剑指 Offer 14- I. 剪绳子
- 剑指 Offer 14- II. 剪绳子 II">剑指 Offer 14- II. 剪绳子 II
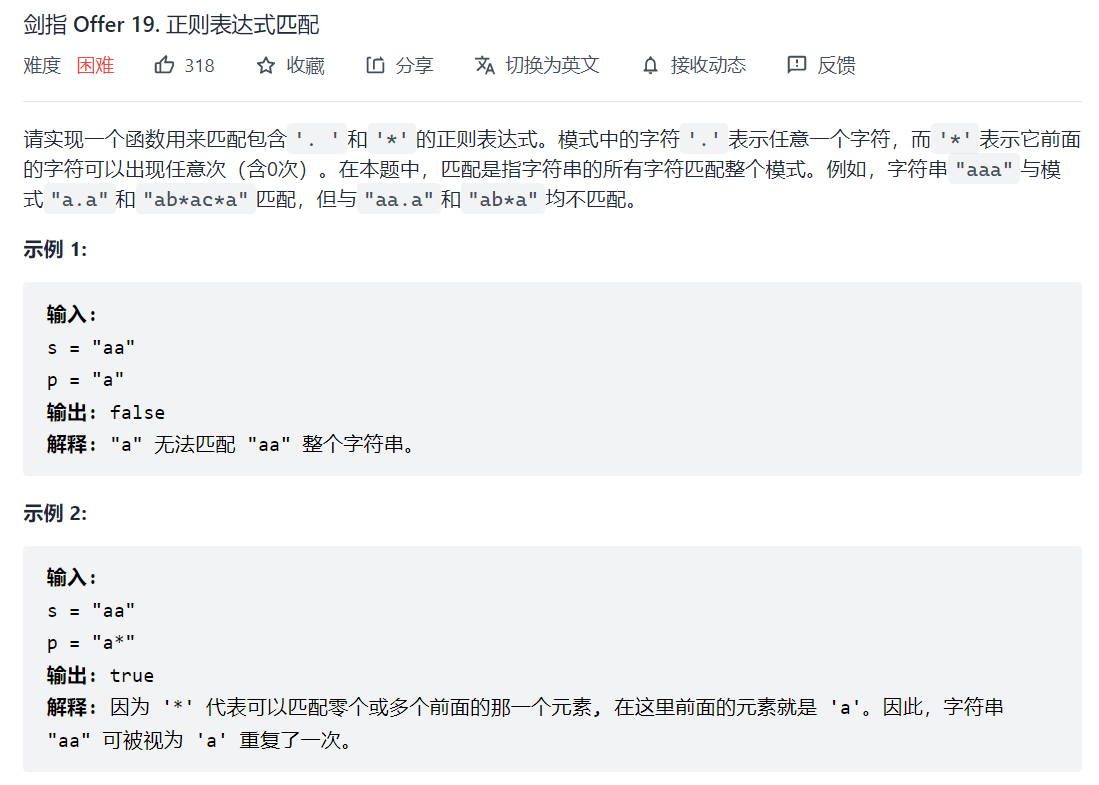
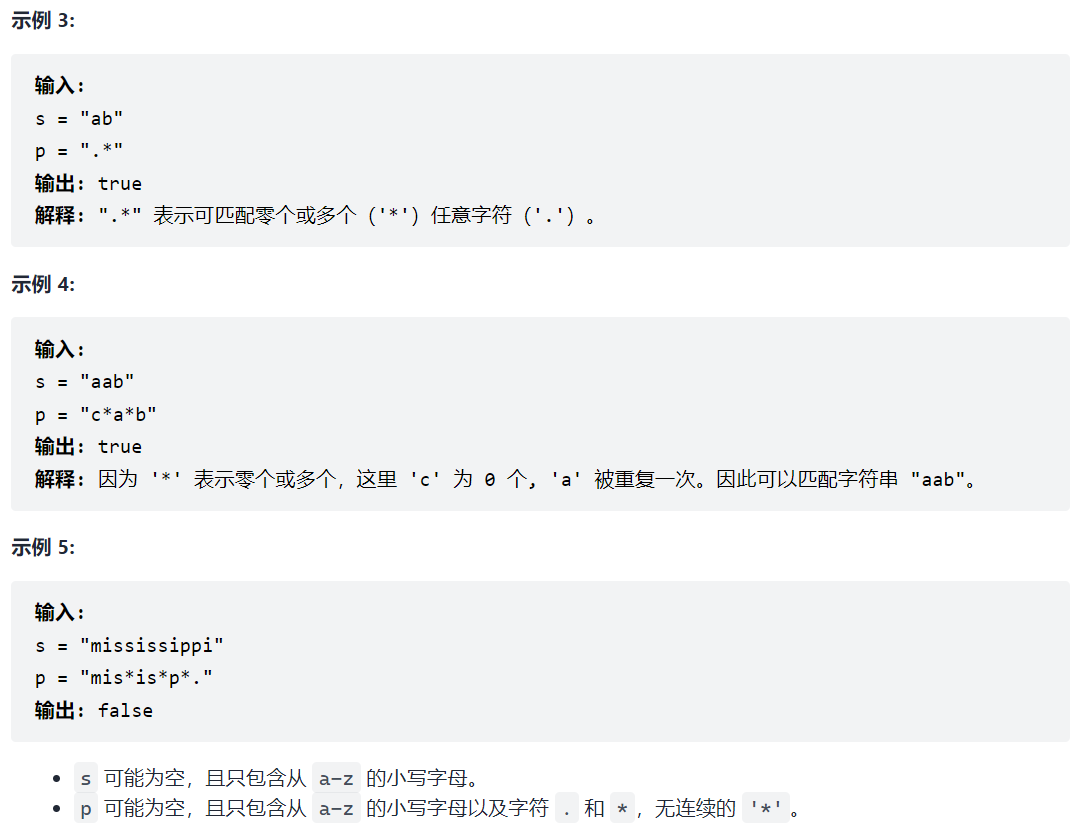
- 剑指 Offer 19. 正则表达式匹配">剑指 Offer 19. 正则表达式匹配
- 剑指 Offer 63. 股票的最大利润">剑指 Offer 63. 股票的最大利润
- 剑指 Offer 42. 连续子数组的最大和">剑指 Offer 42. 连续子数组的最大和
- 剑指 Offer 46. 把数字翻译成字符串💦">剑指 Offer 46. 把数字翻译成字符串💦
- 剑指 Offer 47. 礼物的最大价值">剑指 Offer 47. 礼物的最大价值
- 剑指 Offer 49. 丑数">剑指 Offer 49. 丑数
- 剑指 Offer 63. 股票的最大利润">剑指 Offer 63. 股票的最大利润
剑指 Offer 10- I. 斐波那契数列
最简单的动态规划,不再赘述
要注意的一点是答案超过1e9+7时要进行取模运算
class Solution {public:int fib(int n) {if (n < 2) return n;int pre2 = 0, pre1 = 1;int res;for (int i = 2; i <= n; i++) {res = pre1 + pre2;if (res > 1e9+7) { // 取模res -= 1e9+7;}pre2 = pre1;pre1 = res;}return res;}};
剑指 Offer 10- II. 青蛙跳台阶问题
爬楼梯问题,可按照一般的动态规划来理解,也可以按照完全背包问题来理解
class Solution {public:int numWays(int n) {if (n <= 1) return 1;if (n == 2) return 2;int pre2 = 1, pre1 = 2;int res = 0;for (int i = 2; i < n; i++) {res = pre1 + pre2;if (res > 1e9+7) {res -= 1e9+7;}pre2 = pre1;pre1 = res;}return res;}};
剑指 Offer 14- I. 剪绳子
贪心
根据数学可证明
- 将绳子以相等的长度等分为多段,得到的乘积最大
- 尽可能将绳子以长度3等分为多段,乘积最大(任何大于1的数都可以由一定数目的2和3相加得来)
算法流程: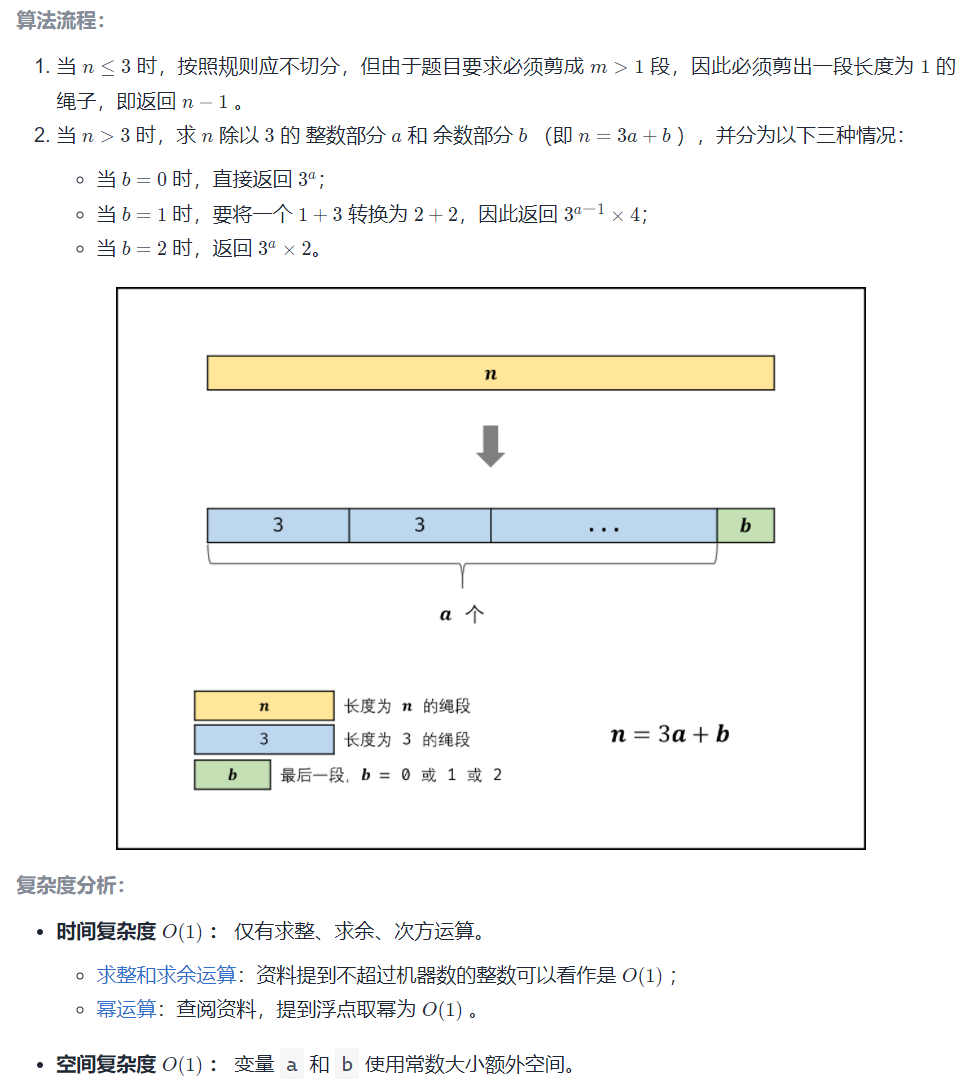
class Solution {public:int cuttingRope(int n) {if (n <= 3) return n - 1;int a = n / 3;int b = n % 3;if (b == 0) return pow(3, a); // 恰好分成n个3if (b == 1) return pow(3, a - 1) * 4; // 将一个3和剩余的1合并为4return pow(3, a) * 2; // 多一个二}};
动态规划
对于长度为n的绳子,将绳子剪一刀,得到长度为m和n-m的两段绳子,长度为n-m的绳子可以剪也可以不剪
通过遍历m就能够得到长度为n的绳子切割和的最大值,采取自底向上遍历减少不必要的计算
// 写法一class Solution {public:int cuttingRope(int n) {if (n == 2)return 1;if (n == 3)return 2;vector<int> dp(n + 1); // dp[i]表示长度为i的绳子切割乘积的最大值// dp[1] = 1;dp[2] = 1; // 切为 1和1// dp[3] = 3; // 长度为3的只能是切成1和2for (int i = 3; i <= n; i++) {int m = 0;for (int j = 1; j <= i / 2; j++) {m = max(j * (i - j), j * dp[i -j]); // 剩下那一段可以剪也可以不剪dp[i] = max(dp[i], m);}}return dp[n];}};
只考虑剪一刀:对于长度为n的绳子,记最大乘积为f(n),假设剪一刀,得到长度为m和n-m的两段绳子,那么切这一刀可以得到的最大乘积为max(f(m) * f(n - m)),
// 写法二
class Solution {
public:
int cuttingRope(int n) {
if (n == 2)
return 1;
if (n == 3)
return 2;
vector<int> dp(n + 1); // dp[i]表示长度为i的绳子切割乘积的最大值
dp[1] = 1;
// 切为 1和1 但是当绳子长度大于2了以后,可以剪为长度为2的段,因此这里初始化为2
// dp[3]的初始化同理
dp[2] = 2;
dp[3] = 3; // 长度为3的只能是切成1和2
for (int i = 4; i <= n; i++) {
int m = 0;
for (int j = 1; j <= i / 2; j++) {
m = max(m, dp[j] * dp[i -j]); // 这里面包含着不切那种情况
dp[i] = m;
}
}
return dp[n];
}
};
考虑剪一刀的动态规划解析:
dp数组用来记录动态规划整个计算过程中的子问题的解和大问题的解。
首先初始化了四个值,分别是,dp数组代表了子问题的解,
代表了绳子长度为3的子问题的最优值就是3,这里不用对长度为3的绳子再进行切割了,因为作为子问题,可以不切,前提是绳子的长度大于3,
代表是已经被切割过为长度为3的子问题的绳子的最优解。
那么看到这里,你会不会有疑问?
为什么要初始化这三个值,为什么不再把的值也预先定义了?
前面说的,动态规划的第二个特点中说到,大问题的最优解依赖于其子问题的最优解,那么记该问题的最优解为,当
时,是不是
的最优解就可以用
来求解呢?
其实也很简单,就列个式子:
解得
当i大于4时,切割后的绳长乘积大于等于不切长度
式子中的表示绳子的长度,
表示对半切,从
开始起,上面这个式子就满足条件了,真实情况下,还要区分奇偶,可以再区分奇偶证明一下,这里就不再证明为奇数的情况了。
所以从开始,绳子就可以进行切割了,即如果问题一开始绳子的长度大于3,比如恰巧等于4,那么可以用来表示。
如果绳子的长度大于4,那么就是一个子问题,这个时候有两种情况:
直接用子问题中绳子的长度(4)来表示。
用
的子问题来求最优解。
前面的式子也证明了,当时,可以采用第2种方法来求解的。
所以其实当i>3时,的解就可以用上面第二种方式来计算了,所以只需要预定义。
[
](https://leetcode-cn.com/problems/jian-sheng-zi-ii-lcof/)
剑指 Offer 14- II. 剪绳子 II

与剪绳子Ⅰ区别在与,这一题需要考虑大数越界的问题。
# 由于语言特性,Python 可以不考虑大数越界问题
class Solution:
def cuttingRope(self, n: int) -> int:
if n <= 3: return n - 1
a, b, p = n // 3, n % 3, 1000000007
if b == 0: return 3 ** a % p
if b == 1: return 3 ** (a - 1) * 4 % p
return 3 ** a * 2 % p
考虑大数越界
class Solution:
def cuttingRope(self, n: int) -> int:
if n <= 3: return n - 1
a, b, p, x, rem = n // 3 - 1, n % 3, 1000000007, 3 , 1
while a > 0:
if a % 2: rem = (rem * x) % p
x = x ** 2 % p
a //= 2
if b == 0: return (rem * 3) % p # = 3^(a+1) % p
if b == 1: return (rem * 4) % p # = 3^a * 4 % p
return (rem * 6) % p # = 3^(a+1) * 2 % p
C++写法
class Solution {
public:
int cuttingRope(int n) {
if (n <= 3)
return n - 1;
long long res = 1;
while (n > 4) {
res *= 3;
res = res % 1000000007;
n -= 3;
}
// 最后的n可能是 4 、3、2,anyway乘上它,就是最大乘积
return (int)(res * n % 1000000007);
}
};
剑指 Offer 19. 正则表达式匹配
剑指 Offer 63. 股票的最大利润

动态规划,定义二维数组
- dp[i][0]表示当前手中持有股票的最大收益
- dp[i][1]表示当前手中没有有股票的最大收益
那么状态转移方程为:
class Solution {
public:
int maxProfit(vector<int>& prices) {
if (prices.size() == 0)
return 0;
int n = prices.size();
vector<vector<int>> dp(2, vector<int>(n, 0));
dp[0][0] = -prices[0];
for (int i = 1; i < n; i++) {
dp[0][i] = max(dp[0][i - 1], -prices[i]); // 因为只交易一次,所以从-price[i]转移
dp[1][i] = max(dp[1][i - 1], dp[0][i - 1] + prices[i]);
}
return dp[1][n - 1];
}
};
贪心:
取左边最大值和右边的最小值
class Solution {
public:
int maxProfit(vector<int>& prices) {
int low = INT32_MAX;
int res = 0;
for (int i = 0; i < prices.size(); i++) {
low = min(low, prices[i]);
res = max(res, prices[i] - low);
}
return res;
}
};
剑指 Offer 42. 连续子数组的最大和
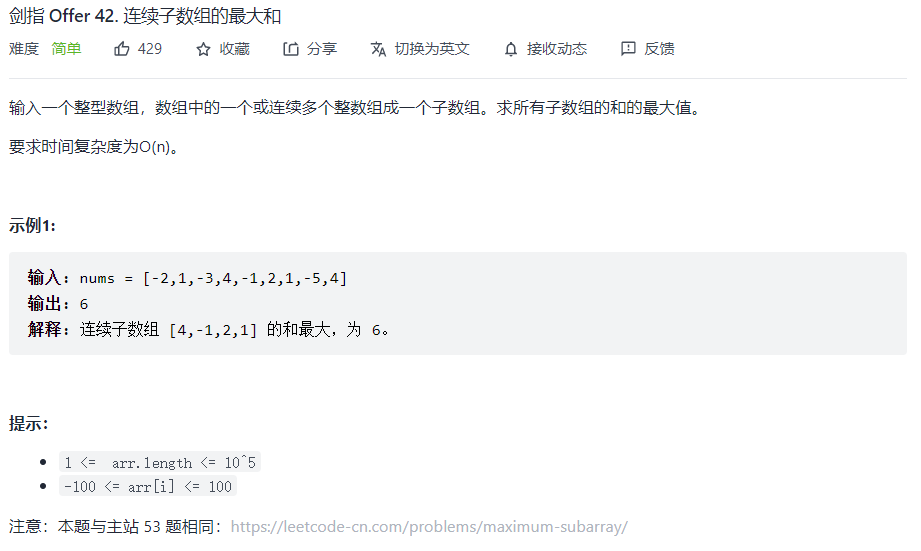
比较经典的动态规划题目
定义dp[i]表示以nums[i]为结尾的最长连续子数组的长度
状态转移方程为
如果dp[i - 1]大于零,那么连续子数组加上nums[i],相当于连续子数组的长度+1,如果其小于0,相当于从nums[i]重新开始一个连续子数组
最后结果应该是dp[i]的最大值
动态规划:
class Solution {
public:
int maxSubArray(vector<int>& nums) {
int n = nums.size();
if (n == 1) return nums[0];
vector<int> dp(n, 0); // dp[i]表示以i为结尾的连续子数组的最大和
dp[0] = nums[0];
int res = dp[0];
for (int i = 1; i < n; i++) {
dp[i] = max(dp[i - 1] + nums[i], nums[i]);
res = max(dp[i], res);
}
return res;
}
};
优化:
class Solution {
public:
int maxSubArray(vector<int>& nums) {
int n = nums.size();
int preMax = nums[0];
int res = preMax;
for (int i = 1; i < n; i++) {
preMax = max(preMax + nums[i], nums[i]);
res = max(preMax, res);
}
return res;
}
};
剑指 Offer 46. 把数字翻译成字符串💦
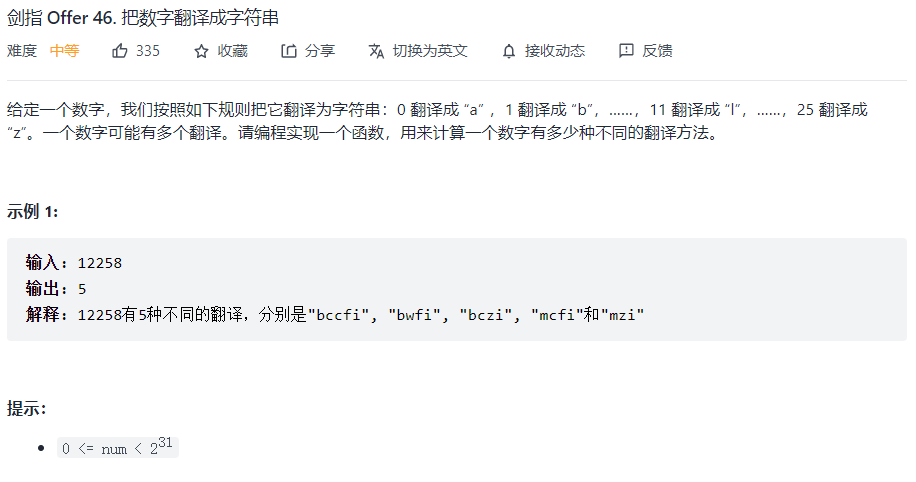
为了方便处理,先将数字转换为字符串,记为s
需要判断两位数字能否组成10 ~ 25之间的数,记dp[i] 为以s[i]为结尾的子串的翻译方法,状态转移方程为
class Solution {
public:
int translateNum(int num) {
if (num < 10) return 1;
string s = to_string(num);
int n = s.size();
vector<int> dp(n, 1); // dp[i]表示以i为结尾的字符串个数
int t = (s[0] - '0') * 10 + s[1] - '0';
if (t >= 10 && t <= 25) {
dp[1] = 2;
}
for (int i = 2; i < n; ++i) {
t = (s[i - 1] - '0') * 10 + s[i] - '0';
if (t >= 10 && t <= 25) {
dp[i] = dp[i - 1] + dp[i - 2];
} else {
dp[i] = dp[i - 1];
}
}
return dp[n - 1];
}
};
class Solution {
public:
int translateNum(int num) {
string src = to_string(num);
int p = 0, q = 0, r = 1;
for (int i = 0; i < src.size(); ++i) {
p = q;
q = r;
r = 0;
r += q;
if (i == 0) {
continue;
}
auto pre = src.substr(i - 1, 2);
if (pre <= "25" && pre >= "10") {
r += p;
}
}
return r;
}
};
剑指 Offer 47. 礼物的最大价值
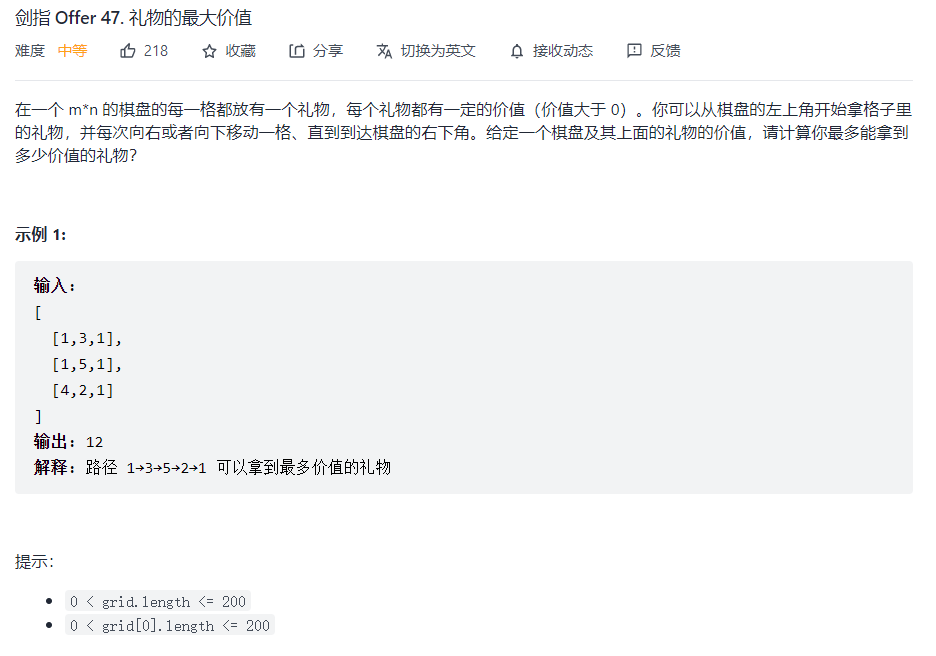
class Solution {
public:
int maxValue(vector<vector<int>>& grid) {
int m = grid.size();
if (m == 0)
return 0;
int n = grid[0].size();
if (n == 0)
return 0;
vector<vector<int>> dp(m, vector<int>(n, 0));
dp[0][0] = grid[0][0];
for (int i = 1; i < m; ++i) {
dp[i][0] = grid[i][0] + dp[i - 1][0];
}
for (int i = 1; i < n; ++i) {
dp[0][i] = grid[0][i] + dp[0][i - 1];
}
for (int i = 1; i < m; ++i) {
for (int j = 1; j < n; ++ j) {
dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]) + grid[i][j];
}
}
return dp[m - 1][n - 1];
}
};
滚动数组优化:
注意到更新dp[i][j]时用到的元素是
- dp[i - 1][j]:当前列,上一行的元素
- dp[i][j - 1]:当前行,上一列的元素
那么可以用一维数组进行优化,dp[j]由dpj和dp[j - 1](已经更新过的上一列的元素)转移来
class Solution {
public:
int maxValue(vector<vector<int>>& grid) {
int m = grid.size();
if (m == 0)
return 0;
int n = grid[0].size();
if (n == 0)
return 0;
vector<int> dp(n + 1, 0); // 为了使 j - 1不越界,定义数组大小为 n + 1
// 初始都为0
for (int i = 1; i <= m; i++) {
for (int j = 1; j <= n; j++) {
dp[j] = max(dp[j], dp[j - 1]) + grid[i - 1][j - 1];
}
}
return dp[n];
}
};
剑指 Offer 49. 丑数
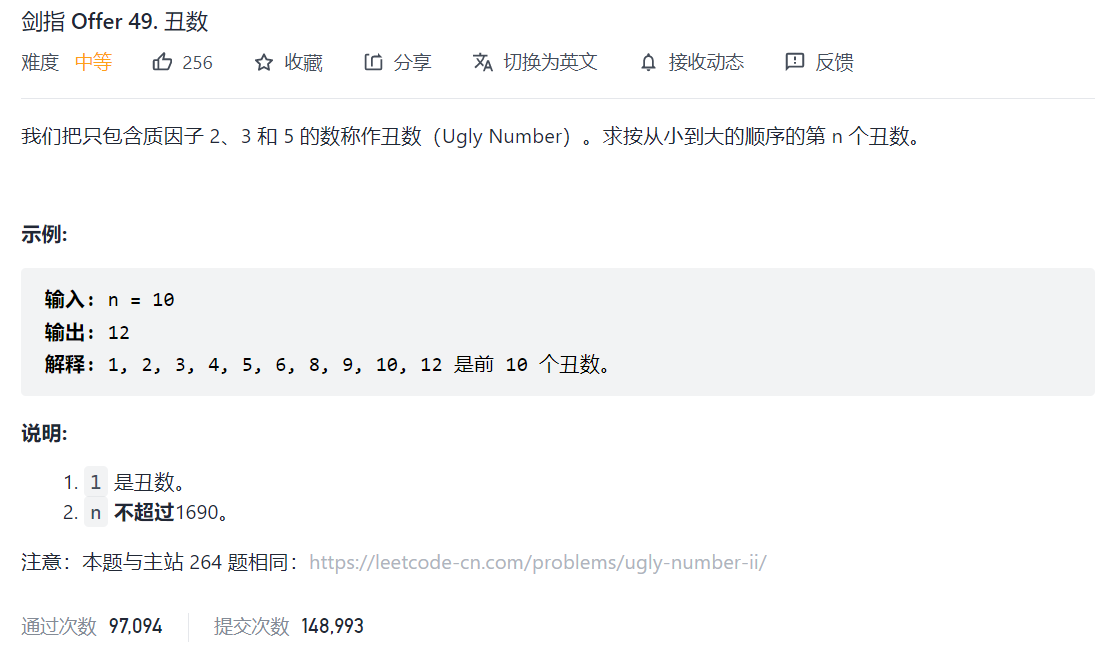
例如 n = 10, primes = [2, 3, 5]。 打印出丑数列表:1, 2, 3, 4, 5, 6, 8, 9, 10, 12
首先一定要知道,后面的丑数一定由前面的丑数乘以2,或者乘以3,或者乘以5得来。例如,8,9,10,12一定是1, 2, 3, 4, 5, 6乘以2,3,5三个质数中的某一个得到。
这样的话我们的解题思路就是:从第一个丑数开始,一个个数丑数,并确保数出来的丑数是递增的,直到数到第n个丑数,得到答案。那么问题就是如何递增地数丑数?
观察上面的例子,假如我们用1, 2, 3, 4, 5, 6去形成后面的丑数,我们可以将1, 2, 3, 4, 5, 6分别乘以2, 3, 5,这样得到一共63=18个新丑数。也就是说1, 2, 3, 4, 5, 6中的*每一个丑数都有一次机会与2相乘,一次机会与3相乘,一次机会与5相乘(一共有18次机会形成18个新丑数),来得到更大的一个丑数。
这样就可以用三个指针,
pointer2, 指向1, 2, 3, 4, 5, 6中,还没使用乘2机会的丑数的位置。该指针的前一位已经使用完了乘以2的机会。
pointer3, 指向1, 2, 3, 4, 5, 6中,还没使用乘3机会的丑数的位置。该指针的前一位已经使用完了乘以3的机会。
pointer5, 指向1, 2, 3, 4, 5, 6中,还没使用乘5机会的丑数的位置。该指针的前一位已经使用完了乘以5的机会。
下一次寻找丑数时,则对这三个位置分别尝试使用一次乘2机会,乘3机会,乘5机会,看看哪个最小,最小的那个就是下一个丑数。最后,那个得到下一个丑数的指针位置加一,因为它对应的那次乘法使用完了。
这里需要注意下去重的问题,如果某次寻找丑数,找到了下一个丑数10,则pointer2和pointer5都需要加一,因为5乘2等于10, 5乘2也等于10,这样可以确保10只被数一次。
class Solution {
public:
int nthUglyNumber(int n) {
vector<int> dp(n);
int x2 = 0, x3 = 0, x5 = 0;
dp[0] = 1;
for (int i = 1; i < n; ++i) {
int n2 = dp[x2] * 2, n3 = dp[x3] * 3, n5 = dp[x5] * 5;
dp[i] = min(n2, min(n3, n5));
if (dp[i] == n2) x2++;
if (dp[i] == n3) x3++;
if (dp[i] == n5) x5++;
}
return dp[n - 1];
}
};
剑指 Offer 63. 股票的最大利润
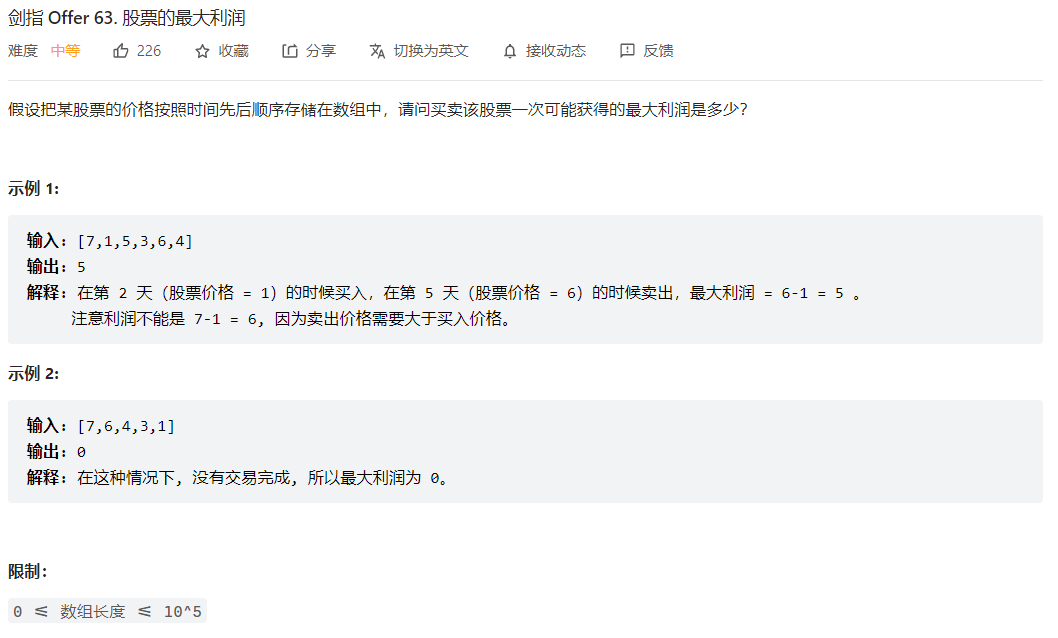
遍历的时候维护一个最小值,如果价格比最小值小,更新最小值,否则计算利润,并更新利润的最大值
class Solution {
public:
int maxProfit(vector<int>& prices) {
if (prices.size() <= 1)
return 0;
int minPrice = prices[0], res = 0;
for (int i = 1; i < prices.size(); ++i) {
if (minPrice > prices[i]) {
minPrice = prices[i];
} else {
res = max(res, prices[i] - minPrice);
}
}
return res;
}
};
动态规划的角度理解:
记dp[i]为前i + 1日利润最大值,dp[i] = max(dp[i - 1], prices[i] - minProfit)

