51. N 皇后

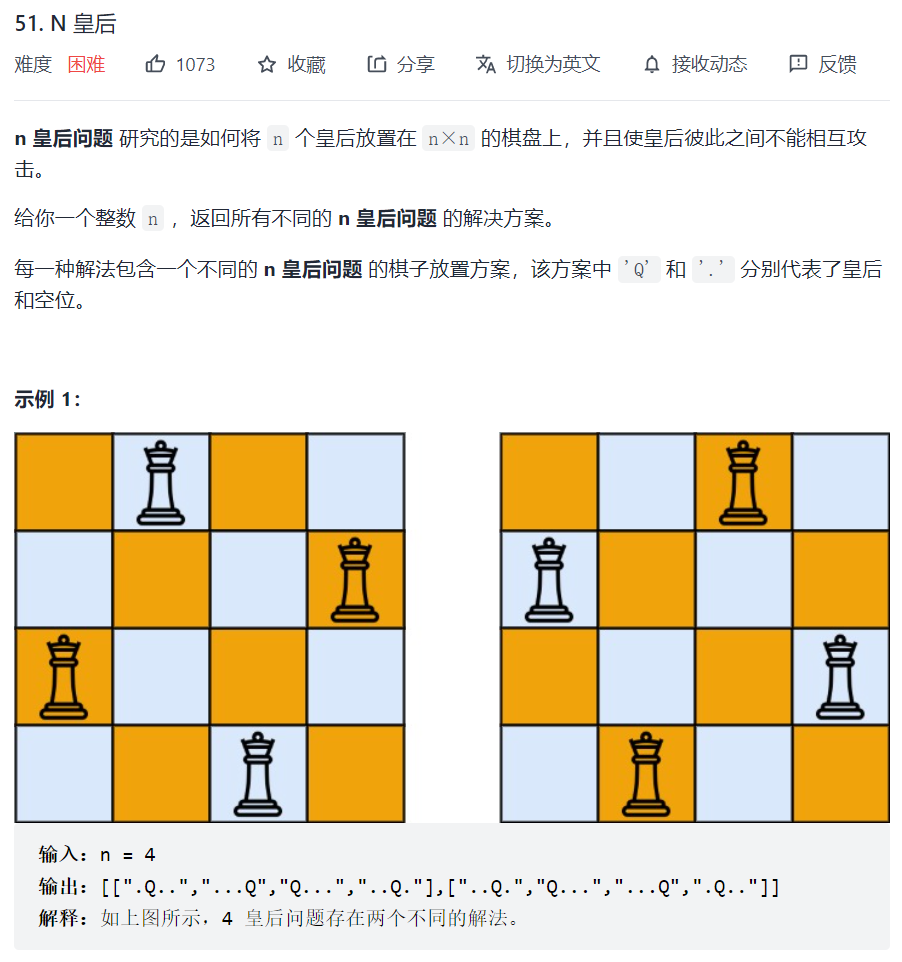
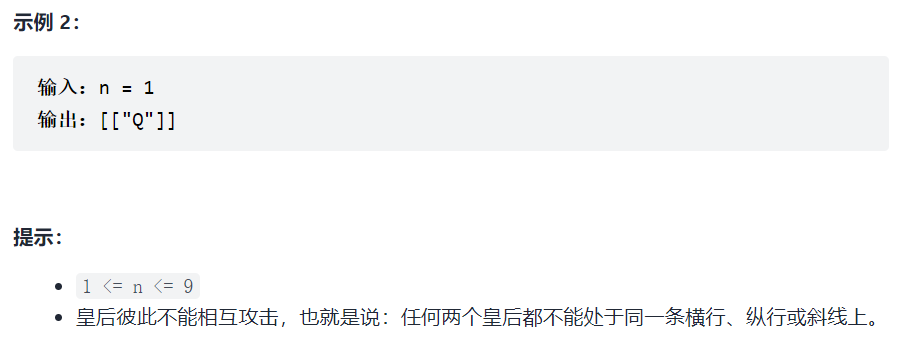
N皇后是经典的回溯问题，给定一个N，在N × N的棋盘上放置N个皇后，使每个皇后之间不能攻击（任何两个皇后不能在同一行、同一列或者一条斜线上）

思路一：直接回溯

完整代码：

class Solution {
public:
    vector<vector<string>> result;
    // n 为输入的棋盘大小
    // row 是当前递归到棋牌的第几行了
    void backtracking(int n, int row, vector<string>& chessboard) {
        if (row == n) {
            result.push_back(chessboard);
            return;
        }
        for (int col = 0; col < n; col++) {
            if (isValid(row, col, chessboard, n)) {//可以放
                chessboard[row][col] = 'Q'; // 放置皇后
                backtracking(n, row + 1, chessboard);
                chessboard[row][col] = '.'; // 回溯，撤销皇后
            }
        }
    }
    bool isValid(int row, int col, vector<string>& chessboard, int n) {
        // 检查列
        for (int i = 0; i < row; i++) {
            if (chessboard[i][col] == 'Q') return false;
        }
        // 检查45度
        for (int i = row - 1, j = col - 1; i >= 0 && j >= 0; i--, j--) {
            if (chessboard[i][j] == 'Q') return false;
        }
        // 检查135度
        for (int i = row -1, j = col + 1; i >=0 && j < n; i--, j++) {
            if (chessboard[i][j] == 'Q') return false;
        }
        return true;
    }
    vector<vector<string>> solveNQueens(int n) {
        vector<string> chessboard(n, string(n, '.'));
        backtracking(n, 0, chessboard);
        return result;
    }
};

思路二：利用组合数

如果把皇后的位置看作是坐标[i, j]，那么生成从1, n的一个排列，得到排列数组，下标记为行数，对应的值记为列数，那么用这个排列就可以确定一个棋盘，并且每个皇后的行数和列数必不相同，因此只需通过判断两个皇后是否处于同一个斜线上，来去掉一些棋盘，就可以得到最终解

完整代码：

class Solution {
public:
    vector<vector<string>> result;
    vector<int> path;

    void backtracking(int n, int row, vector<string>& chessboard, vector<bool>& used) {
        if (row == n) {
            bool flag = true;
            for (int i = 0; i < n; i++) {
                for (int j = i + 1; j < n; j++) {
                    if (abs(i - j) == abs(path[i] - path[j])) // 在一对角线上
                        flag = false;
                }
            }
            if (flag)
                result.push_back(chessboard);
            return;
        }
        for (int i = 0; i < n; i++) {
            if (!used[i]) {
                path.push_back(i);
                chessboard[row][i] = 'Q';
                used[i] = true;
                backtracking(n, row + 1, chessboard, used);
                path.pop_back();
                chessboard[row][i] = '.';
                used[i] = false;
            }
        }

    }

    vector<vector<string>> solveNQueens(int n) {
        vector<string> chessboard(n, string(n, '.'));
        vector<bool> used(n, false);
        backtracking(n, 0, chessboard, used);
        return result;
    }
};

剪枝

在生成棋盘的过程中进行判断，如果前面存在处于统一斜线的皇后，直接终止

class Solution {
public:
    vector<vector<string>> res;
    vector<int> p; // 生成的排列
    void dfs(vector<string>& c, int start, vector<bool>& used) {
        if (start == c.size()) {
            res.push_back(c);
            return;
        }
        for (int i = 0; i < c.size(); ++i) {
            if (!used[i]) {
                bool flag = true;
                for (int j = 0; j < p.size(); ++j) { // 判断之前的queen是否和当前要放置的处于同一对角线
                    if (abs(start - j) == abs(i - p[j])) { // start是当前queen的横坐标，i是纵坐标
                        flag = false;
                        break;
                    }
                }
                if (flag) {
                    c[start][i] = 'Q';
                    p.push_back(i);
                    used[i] = true;
                    dfs(c, start + 1, used);
                    used[i] = false;
                    p.pop_back();
                    c[start][i] = '.';
                }

            }
        }
    }
    vector<vector<string>> solveNQueens(int n) {
        vector<bool> used(n, false);
        vector<string> c(n, string(n, '.'));
        dfs(c, 0, used);
        return res;
    }
};

可以看到，剪枝不剪枝差别还是很大的