46. 全排列

与组合问题不同，排列问题有序，{1， 2} 和{2，1}是两个不同的排列，一个元素使用过一次，再另一个排列中还要使用，因此横向的搜索不能从startIndex处开始搜索，每次都要从头开始，这时候每个元素在每一个排列中只能出现一次，因此，需要一个used数组，来表示当前排列中，对应位置的元素是否使用过。

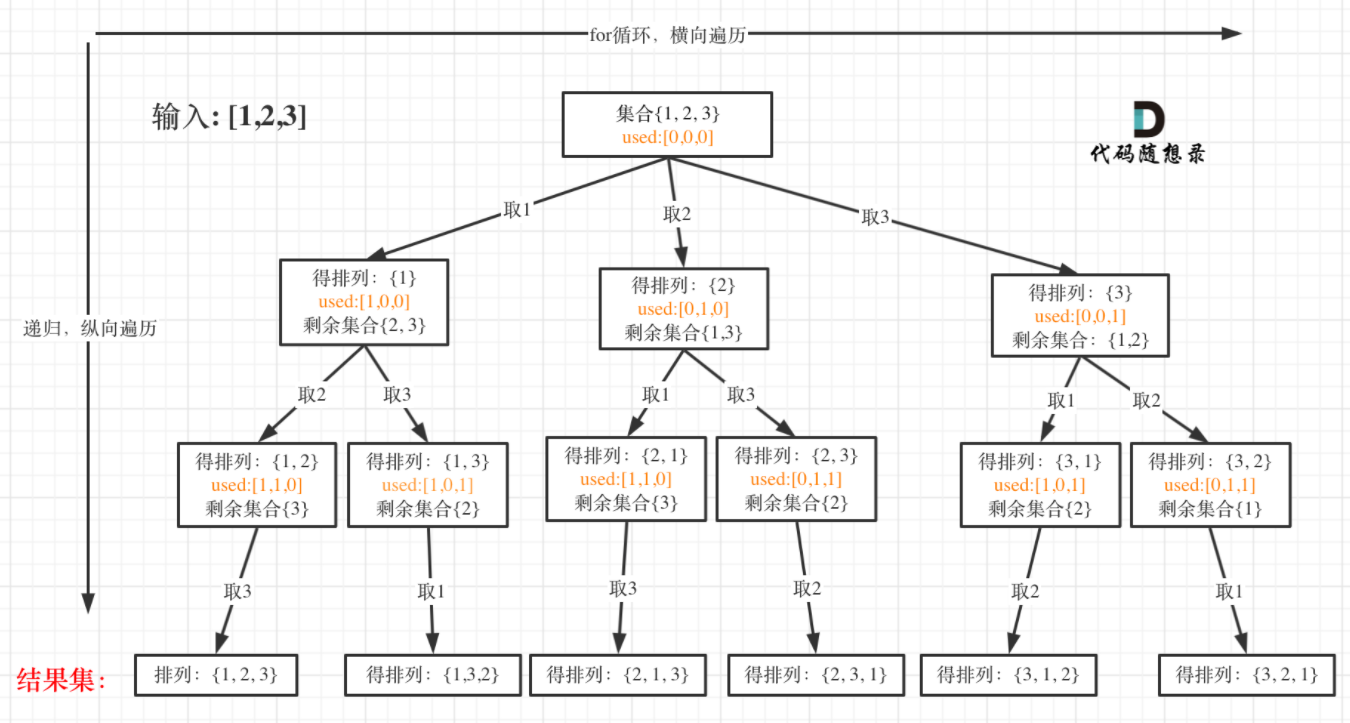
class Solution {
public:
    vector<vector<int>> res;
    vector<int> path;
    void dfs(vector<int>& nums, vector<bool>& used) {
        if (path.size() == nums.size()) {
            res.push_back(path);
            return;
        }
        // for 横向遍历确定当前位置的值，递归来选择下一个位置的值，用used保证当前位置和下一个位置不会重复
        for (int i = 0; i < nums.size(); ++i) {
            if (!used[i]) {
                path.push_back(nums[i]);
                used[i] = true;
                dfs(nums, used);
                used[i] = false;
                path.pop_back();
            }
        }
    }
    vector<vector<int>> permute(vector<int>& nums) {
        vector<bool> used(nums.size(), false);
        dfs(nums, used);
        return res;
    }
};

47. 全排列 II

通过此题来了解全排列的去重操作
首先，去重操作一定要先排序，以方便通过相邻元素来判断该层是否用过相同数值的元素

used[i - 1]等于true的时候，上一个位置用过nums[i - 1]，因为nums[i]和nums[i - 1]是值相同的两个数，这个位置可以使用nums[i]

used[i - 1]等于false时，i的下标逐渐增大,一定是used[i - 1]变为ture后又回溯为false,即这个位置使用过nums[i]这个数字，再使用就会重复

class Solution {
public:
  vector<vector<int>> res;
  vector<int> path;
  void dfs(vector<int>& nums, vector<bool>& used) {
      if (path.size() == nums.size()) {
          res.push_back(path);
          return;
      }
      for (int i = 0; i < nums.size(); ++i) {
          if (i > 0 && nums[i] == nums[i - 1] && used[i - 1] == false) continue; // 当前位置使用过这个数字
          if (!used[i]) {
              path.push_back(nums[i]);
              used[i] = true;
              dfs(nums, used);
              used[i] = false;
              path.pop_back();
          }
      }
  }
  vector<vector<int>> permuteUnique(vector<int>& nums) {
      sort(nums.begin(), nums.end());
      vector<bool> used(nums.size(), false);
      dfs(nums, used);
      return res;
  }
};