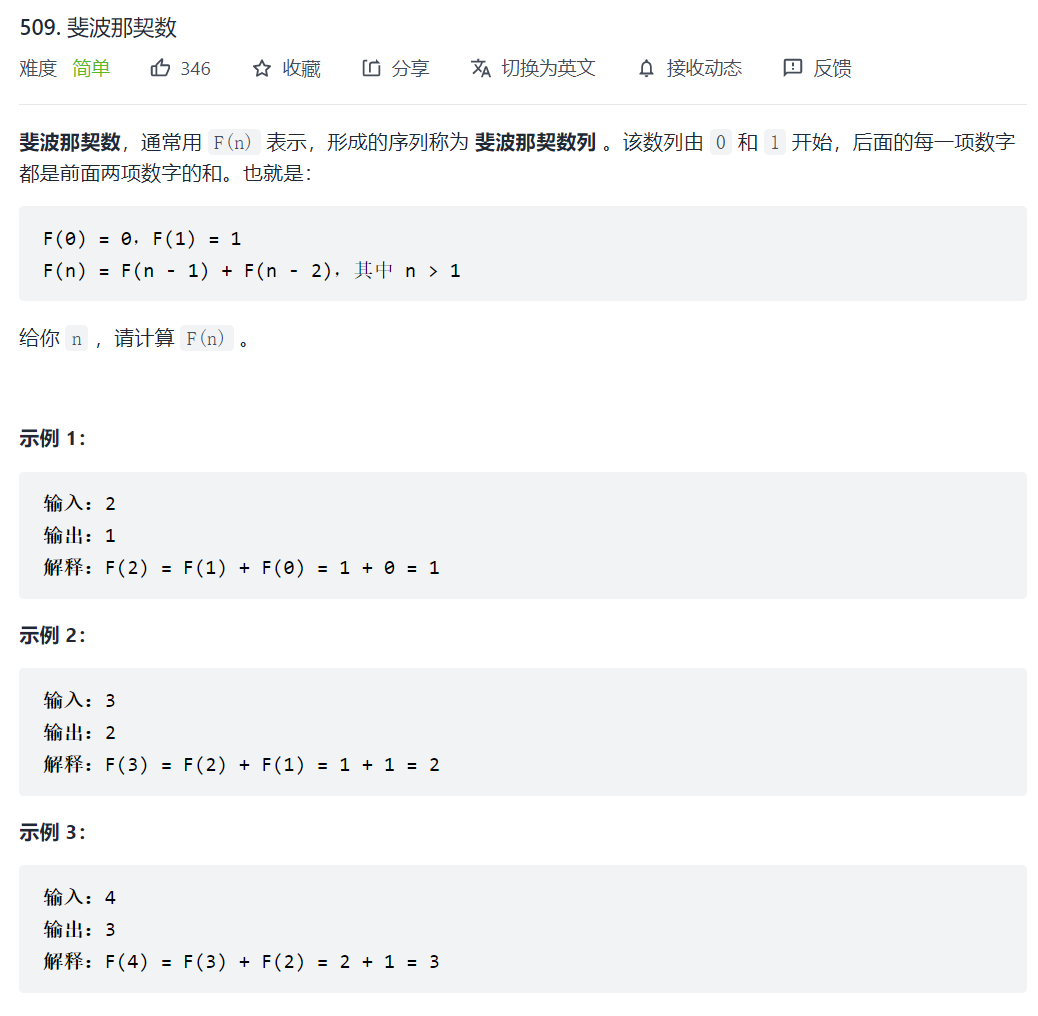
509. 斐波那契数
思路一:递归
代码很简单
class Solution {public:int fib(int n) {if (n < 2) return n;return fib(n - 1) + fib(n - 2);}};
但是可以用一个数组来保存几经计算过的数值,避免重复计算,降低时间复杂度
带备忘录的递归:
class Solution {
public:
int helper(int n, vector<int>& dp) {
if (n < 2) return n;
if (dp[n] == -1)
dp[n] = helper(n - 1, dp) + helper(n - 2, dp);
return dp[n];
}
int fib(int n) {
if (n < 2) return n;
vector<int> dp(n + 1, -1);
dp[0] = 0;
dp[1] = 1;
return helper(n, dp);
}
};
思路二:迭代
状态转移方程 dp[i] = dp[i - 1] + dp[i - 2];
class Solution {
public:
int fib(int n) {
if (n < 2) return n;
vector<int> dp(n + 1, 0);
dp[1] = 1;
for (int i = 2; i <= n; i++) {
dp[i] = dp[i - 1] + dp[i - 2];
}
return dp[n];
}
};
通过只维护两个变量来降低空间复杂度
class Solution {
public:
int fib(int n) {
if (n < 2) return n;
int pre1 = 1, pre2 = 0;
int res;
for (int i = 2; i <= n; i++) {
res = pre2 + pre1;
pre2 = pre1;
pre1 = res;
}
return res;
}
};
70. 爬楼梯
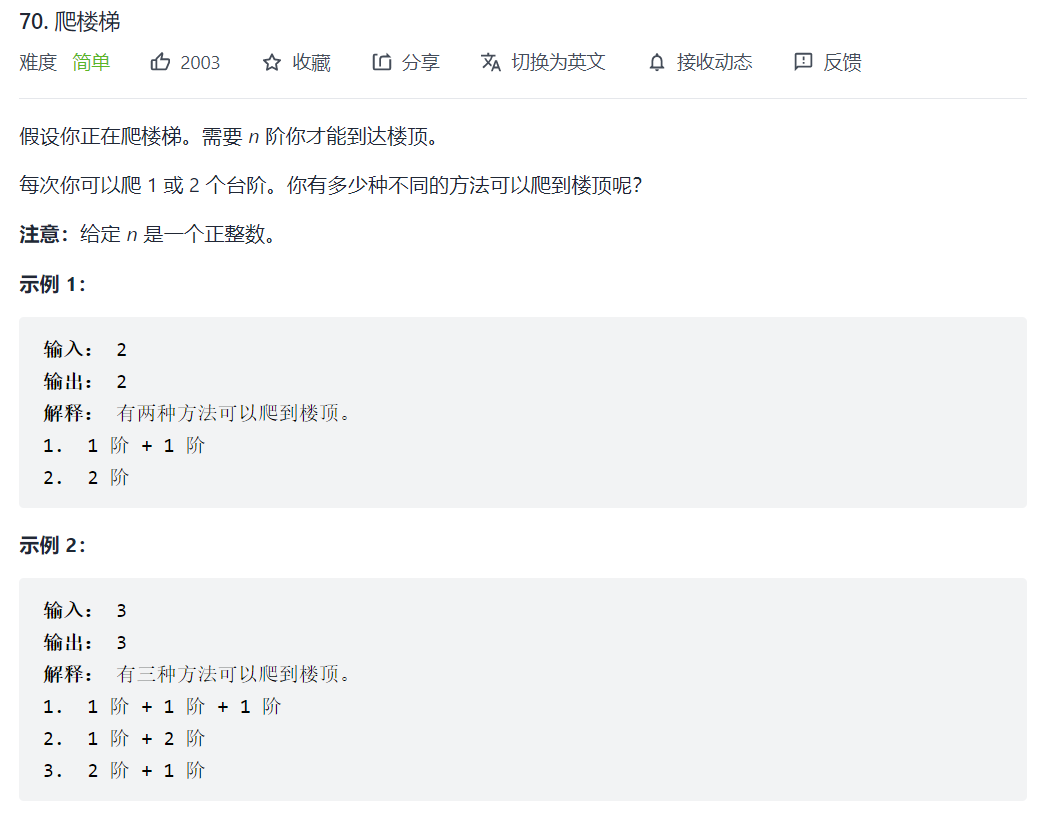
这道题和斐波那契数其实是一样的,每个楼梯都有两种方式到达,从前两节跳两步,从前一节跳一步,于是有了状态转移方程
初始状态,dp[1] = 0, dp[2] = 2(从地上一次两阶,或者一次一阶跳两次)
直接递归会超时,不多赘述,代码和斐波那契也差不多
用dp数组
class Solution {
public:
int climbStairs(int n) {
//用递归会超时,改用自底向上法
if (n == 1 || n == 2)
return n;
vector<int> dp(n + 1);
dp[1] = 1;
dp[2] = 2;
for (int i = 3; i <= n; i++) {
dp[i] = dp[i - 1] + dp[i - 2];
}
return dp[n];
}
};
维护两个变量
class Solution {
public:
int climbStairs(int n) {
//用递归会超时,改用自底向上法
if (n == 1 || n == 2)
return n;
int pre2 = 1, pre1 = 2, cur;
for (int i = 2; i < n; i++) { // i只代表迭代次数 i=2只当前在第三节
cur = pre1 + pre2;
pre2 = pre1;
pre1 = cur;
}
return cur;
}
};
746. 使用最小花费爬楼梯
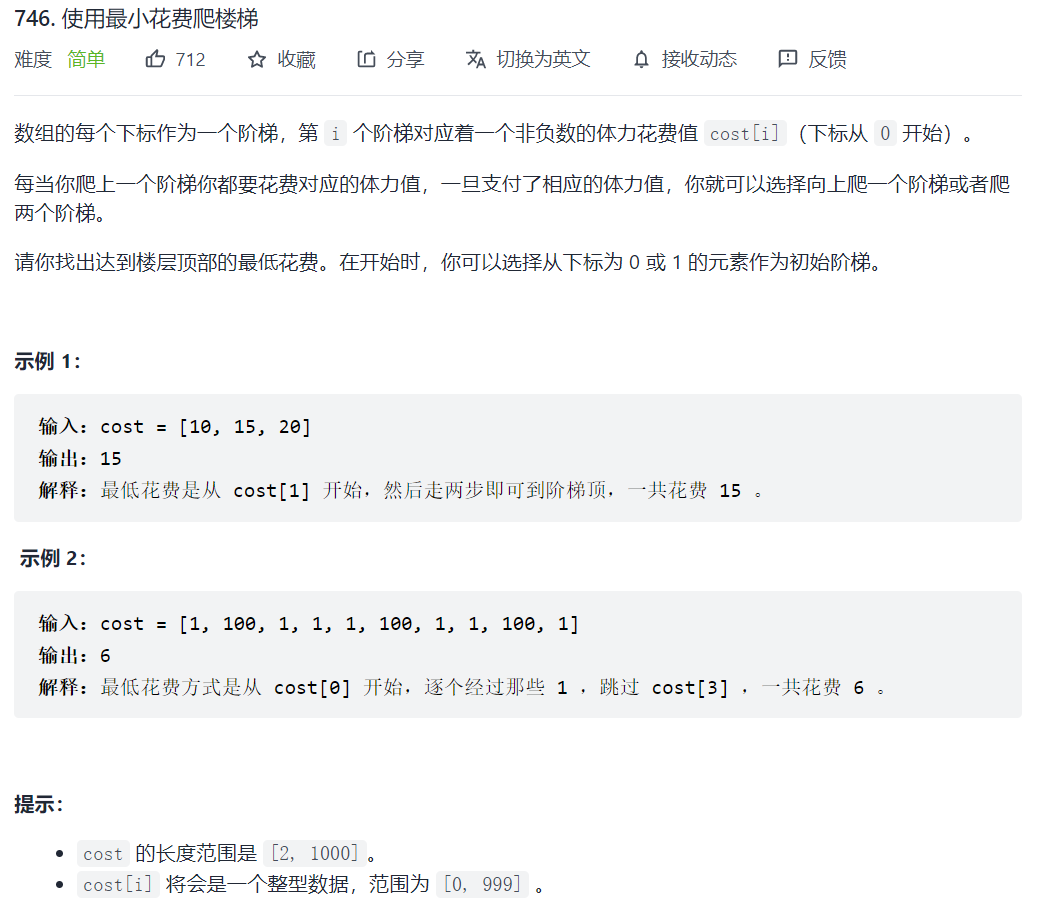
解决动态规划问题的五个步骤:
代码:
class Solution {
public:
int minCostClimbingStairs(vector<int>& cost) {
int n = cost.size();
vector<int> dp(n + 1, 0); // cost共n个,下标n代表楼层顶部
for (int i = 2; i < n + 1; i++) {
dp[i] = min(dp[i - 1] + cost[i - 1], dp[i - 2] + cost[i - 2]);
}
return dp[n];
}
};
优化空间复杂度
class Solution {
public:
int minCostClimbingStairs(vector<int>& cost) {
int pre1 = 0, pre2 = 0;
int res;
for (int i = 2; i <= cost.size(); i++) {
res = min(pre1 + cost[i - 1], pre2 + cost[i - 2]);
pre2 = pre1;
pre1 = res;
}
return res;
}
62. 不同路径
动态规划
这道题是一个二维的动态规划问题,用一个二维数组dp来记录到达每个位置有几种方法,那么可以得到状态转移公式
表示当前位置可以由左面向右走一步或者由上面向下走一步到达。
初始状态:
dp[0][0] = 1,dp[i][1] = 1, dp[1][j] = 1
然后从左到右一层一层的遍历就可以得到完整的dp数组
最后返回dp[m][n]即可
class Solution {
public:
int uniquePaths(int m, int n) {
vector<vector<int>> dp(m + 1, vector<int>(n + 1, 1));
// 从第二行第二列开始处理
for (int i = 2; i <= m; i++) {
for (int j = 2; j <= n; j++) {
dp[i][j] = dp[i-1][j] + dp[i][j-1];
}
}
return dp[m][n];
}
};
优化空间(滚动数组):
只用一个一维数组dp来记录每一行的结果,因为我们以一行一行的遍历,因为未更新这个一维数组之前,其保存的是上一行的结果。在二维dp中,dp[i][j]为上面和左面的元素之和,使用一个数组,dp未更新前,dp[i]为上一行的结果,dp[i-1]更新后,保存的是左边的结果,那么状态转移方程为:
class Solution {
public:
int uniquePaths(int m, int n) {
vector<int> dp(n + 1, 0);
dp[1] = 1;
for (int i = 1; i <= m; ++i)
for (int j = 1; j <= n; ++j)
dp[j] += dp[j - 1];
return dp[n];
}
};
思路三:数论方法
从起点走到终点,一共需要 m + n - 2步(其中 m-1步向下,n-1步向右)
那么问题可以转化为,从 m + n - 2 中,选择 m - 1 步向下,有多少种选法,那么答案为
其中:
求组合的时候,要防止两个int相乘溢出! 所以不能把算式的分子都算出来,分母都算出来再做除法。
class Solution {
public:
int uniquePaths(int m, int n) {
long long ans = 1;
for (int x = n, y = 1; y < m; ++x, ++y) {
ans = ans * x / y;
}
return ans;
}
};
63. 不同路径 II
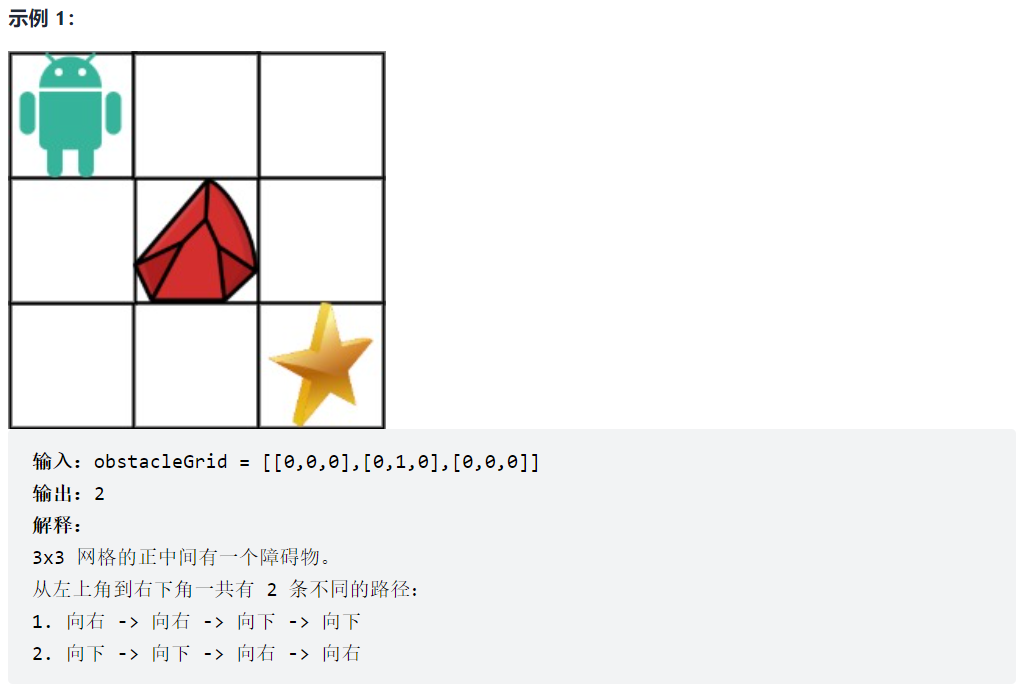
这道题相较于62题多了障碍物,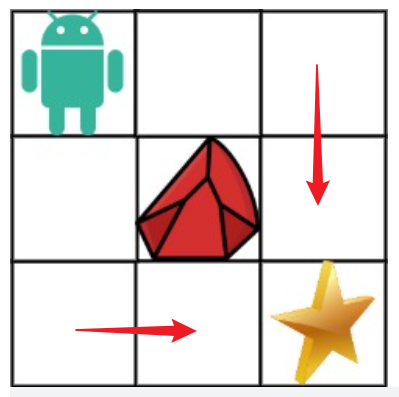
也就是说,障碍物右边或者下边的的位置,被封锁了一条路,在更新dp数组时,只能加一个数,也就是
dp[1][2] = 0 + dp[0][2],dp[2][1] = dp[0][2] + 0
那么将有障碍物的位置,保持初始值0,即可。如果有一个倒霉蛋,上面是障碍物,下面也是障碍物,那么就到不了这个位置了。
class Solution {
public:
int uniquePathsWithObstacles(vector<vector<int>>& obstacleGrid) {
int m = obstacleGrid.size(), n = obstacleGrid[0].size();
vector<vector<int>> dp(m, vector<int>(n, 0));
// 第一列的数,如果出现障碍物,障碍物的下面都无法到达
for (int i = 0; i < m && obstacleGrid[i][0] == 0; i++) dp[i][0] = 1;
// 第一行的数,如果出现障碍物,障碍物的右面都无法到达
for (int i = 0; i < n && obstacleGrid[0][i] == 0; i++) dp[0][i] = 1;
for (int i = 1; i < m; i++) {
for (int j = 1; j < n; j++) {
if (obstacleGrid[i][j] == 0) { // 只更新没有障碍物的地方
dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
}
}
}
return dp[m - 1][n - 1];
}
};
利用滚动数组优化:
class Solution {
public:
int uniquePathsWithObstacles(vector<vector<int>>& obstacleGrid) {
int m = obstacleGrid.size(), n = obstacleGrid[0].size();
vector<int> dp(n + 1, 0);
dp[1] = obstacleGrid[0][0] ? 0 : 1;
for (int i = 1; i <= m; ++i)
for (int j = 1; j <= n; ++j)
if (obstacleGrid[i - 1][j - 1] == 0) // 没有障碍物更新
dp[j] += dp[j - 1];
else
dp[j] = 0; // 有障碍物则更新为0
return dp[n];
}
};

64. 最小路径和
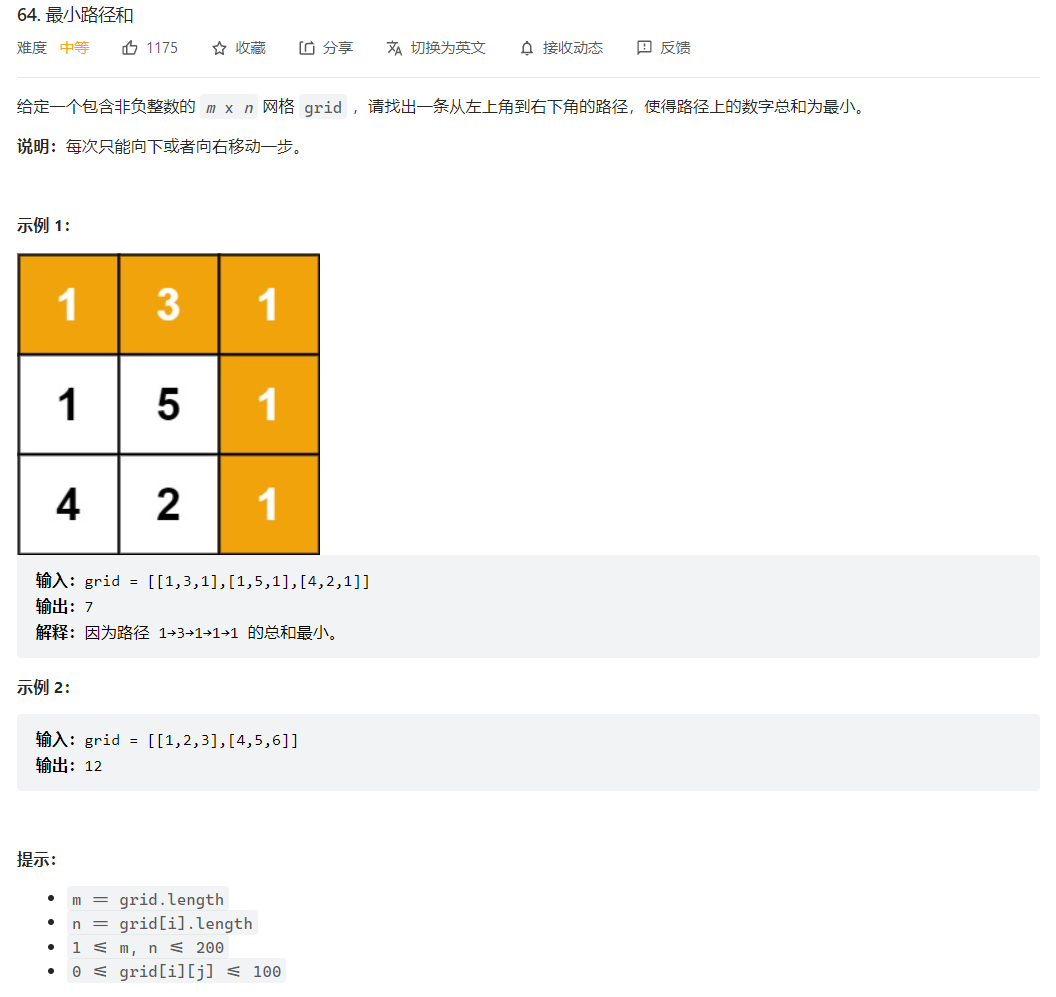
在原数组上操作:
class Solution {
public:
int minPathSum(vector<vector<int>>& grid) {
if (grid.size() == 0 || grid[0].size() == 0) return 0;
int m = grid.size(), n = grid[0].size();
for (int i = 1; i < m; ++i) grid[i][0] += grid[i - 1][0];
for (int i = 1; i < n; ++i) grid[0][i] += grid[0][i - 1];
for (int i = 1; i < m; ++i) {
for (int j = 1; j < n; ++j) {
grid[i][j] += min(grid[i - 1][j], grid[i][j - 1]);
}
}
return grid[m - 1][n - 1];
}
};
class Solution {
public:
int minPathSum(vector<vector<int>>& grid) {
if (grid.size() == 0 || grid[0].size() == 0) return 0;
int m = grid.size(), n = grid[0].size();
vector<vector<int>> dp(m , vector<int>(n, 0));
dp[0][0] = grid[0][0];
for (int i = 1; i < m; ++i) {
dp[i][0] = dp[i - 1][0] + grid[i][0];
}
for (int i = 1; i < n; ++i) {
dp[0][i] = dp[0][i - 1] + grid[0][i];
}
for (int i = 1; i < m; ++i) {
for (int j = 1; j < n; ++j) {
dp[i][j] = min(dp[i - 1][j], dp[i][j - 1]) + grid[i][j];
}
}
return dp[m - 1][n - 1];
}
};
优化空间复杂度后:
因为要求最小值,需要将dp数组初始化为INT32_MAX
class Solution {
public:
int minPathSum(vector<vector<int>>& grid) {
int m = grid.size(), n = grid[0].size();
vector<int> dp(n + 1, INT32_MAX); // 求最小值一定要将初值设的大一点
dp[1] = 0;
for (int i = 0; i < m; ++i)
for (int j = 1; j <= n; ++j)
dp[j] = min(dp[j - 1], dp[j]) + grid[i][j - 1];
return dp[n];
}
};
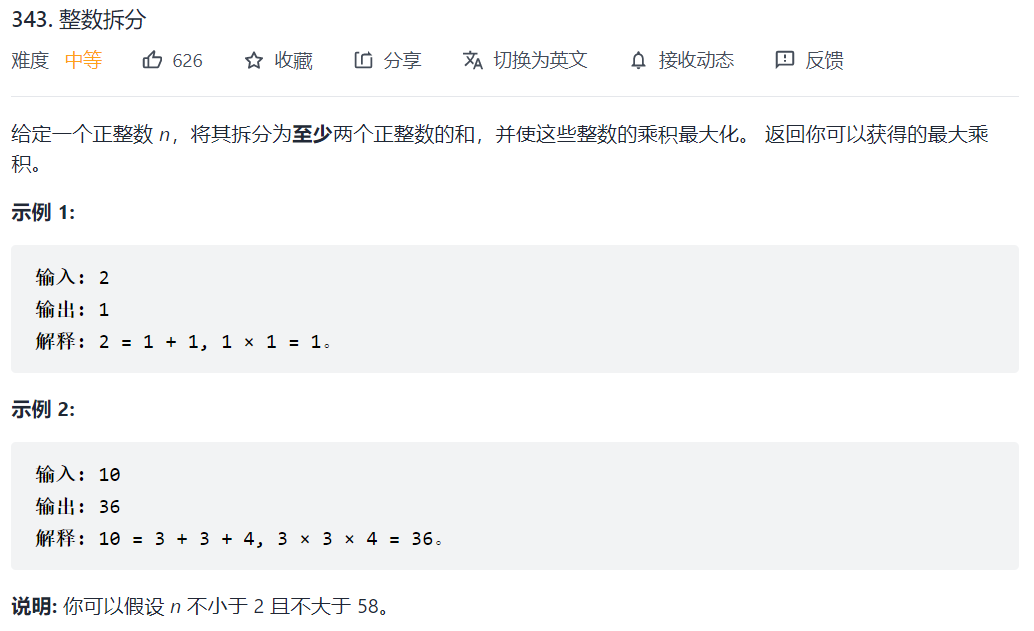
343. 整数拆分
贪心
尽可能的多拆出3来,3越多,乘积越大
class Solution {
public:
int integerBreak(int n) {
if (n == 2) return 1;
if (n == 3) return 2;
int x = n % 3;
int res;
if (x == 0) {
res = pow(3, n / 3);
} else if (x == 1) {
res = pow(3, n / 3 - 1) * 4;
} else {
res = pow(3, n / 3) * 2;
}
return res;
}
};
动态规划
这道题就是切割钢条的思想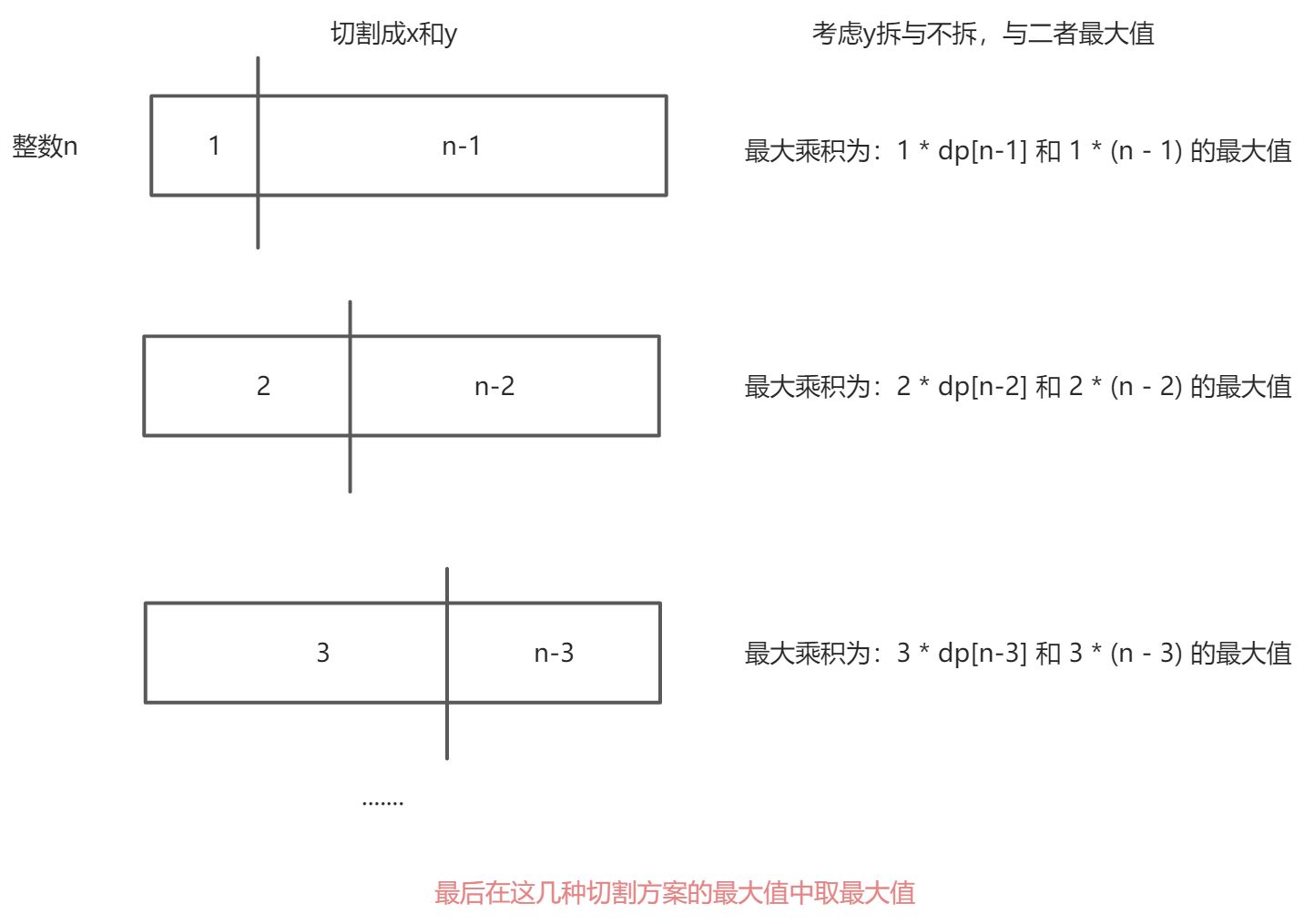
将数n拆分成 x, y
通过dp数组,记录1~n每个数字的最佳切割方案(记录x和y的最大乘积)
假设将 i 切为 j 和 i - j ,j 在 1 ~ i-1 之间迭代,那么状态转移方程为:
- dp[i]:使用之前拆分乘积的最大值
- (i - j) * j : 只拆为这两段
- dp[i -j] * j:i - j 继续拆
定义一个dp数组,dp[i]表示整数i拆分后的最大乘积,1和0都不能拆分,dp[0]和dp[1]都是0
class Solution {
public:
int integerBreak(int n) {
vector<int> dp(n + 1, 0);
// 初始化0,1
for (int i = 0; i <= n; i++) {
for (int j = 1; j < i; j++) {
dp[i] = max(dp[i], max(j * dp[i - j], j * (i - j)));
}
}
return dp[n];
}
};
另一种写法(都一样):
对于每个dp[i]来说,假设拆分出一个 j 出来, 会有
//curMax记录对于不同拆分情况(遍历j)乘积的最大值
dp[i] = max(curMax,max(j * (i - j), j * dp[i - j]));
class Solution {
public:
int integerBreak(int n) {
vector<int> dp(n + 1);
dp[0] = 0;
dp[1] = 0;
for (int i = 2; i <= n; ++i) {
int curMax = 0;
for (int j = 1; j < i; ++j) {
curMax = max(curMax, max(j * (i - j), j * dp[i - j]));
}
dp[i] = curMax;
}
return dp[n];
}
};
赖皮做法,查表。因为 2 ≤ n ≤ 58
class Solution {
public:
int integerBreak(int n) {
vector<int> res{0, 0, 1, 2, 4, 6, 9, 12, 18, 27, 36, 54, 81, 108, 162, 243, 324, 486, 729, 972, 1458, 2187, 2916, 4374, 6561, 8748, 13122, 19683, 26244, 39366, 59049, 78732, 118098, 177147, 236196, 354294, 531441, 708588, 1062882, 1594323, 2125764, 3188646, 4782969, 6377292, 9565938, 14348907, 19131876, 28697814, 43046721, 57395628, 86093442, 129140163, 172186884, 258280326, 387420489, 516560652, 774840978, 1162261467, 1549681956};
return res[n];
}
};
96. 不同的二叉搜索树
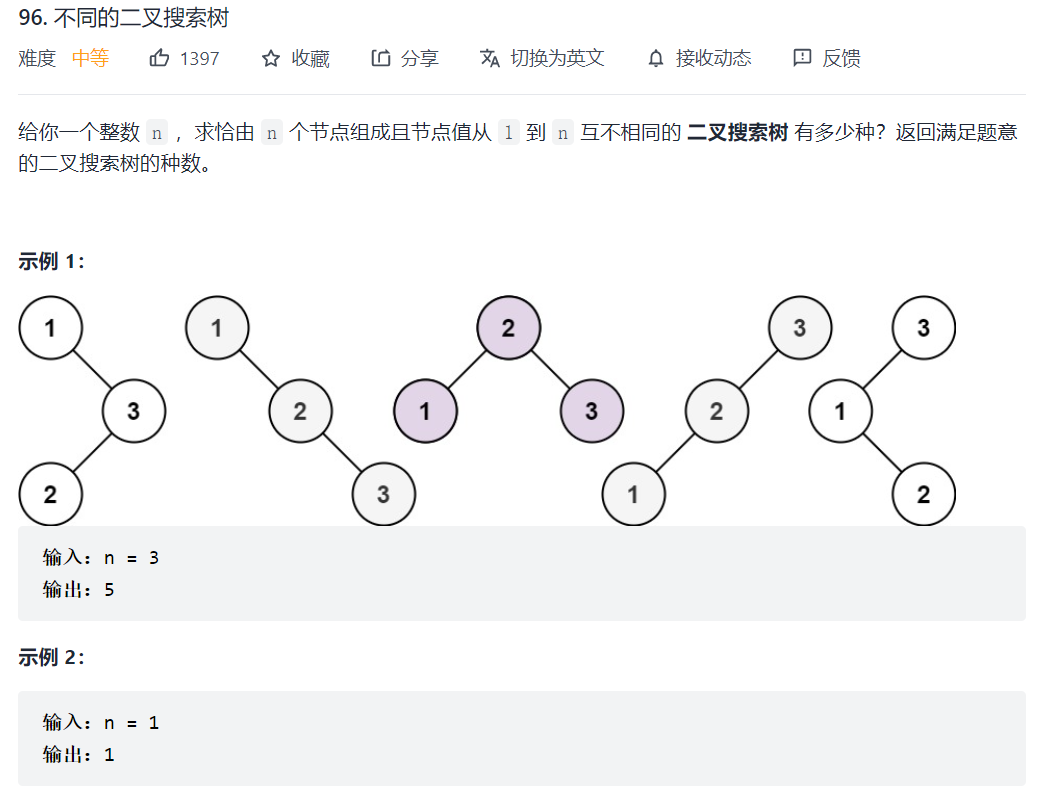
因为求不同树的数量,并不用把搜索树都列出来,所以不用关心其具体数值的差异
动态规划
定义两个函数:
G(n): 长度为 n的序列能构成的不同二叉搜索树的个数。
F(i, n):以 i为根、序列长度为 nn 的不同二叉搜索树个数 (1≤i≤n)。
那么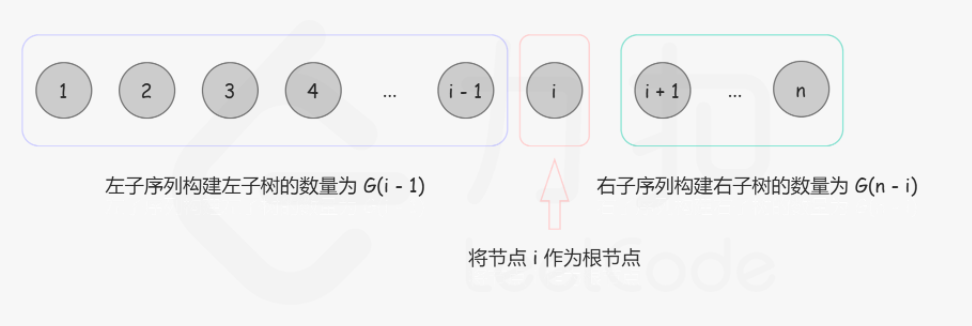
每次以1~n中的不同节点 i 作为根的搜索树数量为 :以 1~i 能够构建搜索树的数量(左子树) 乘以 i~n 能够构建搜索树的数量(右子树)
有
两公式联立可以得到:
完整代码:
class Solution {
public:
int numTrees(int n) {
vector<int> dp(n + 1);
dp[0] = 1; // 空节点也可以看作是一棵二叉搜索树
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= i; j++) { // 计算以j为根结点的搜索树数目
dp[i] += dp[j - 1] * dp[i - j]; // 左子树的数量乘以右子树的数量就是以j为根结点的数目
}
}
return dp[n];
}
};
数学法
动态规划推导的,是卡塔兰数
卡塔兰数:
class Solution {
public:
int numTrees(int n) {
long long C = 1;
for (int i = 0; i < n; ++i) {
C = C * 2 * (2 * i + 1) / (i + 2);
}
return (int)C;
}
};
413. 等差数列划分

记dp[i]为以nums[i]为结尾的等差子数组个数,因为子数组最小为3,从第三个元素开始遍历,如果该元素与它前面的两个元素构成等差数列,那么dp[i] = dp[i - 1] + 1。解释:以nums[i - 1]为结尾的等差子数组个数为
dp[i - 1],那么这dp[i - 1]个子数组都可以加上nums[i]构成新的子数组,并且nums[i - 2]、nums[i - 1]、nums[i]也是一个等差子数组
最后返回的应该是dp的和
class Solution {
public:
int numberOfArithmeticSlices(vector<int>& nums) {
int n = nums.size();
if (n < 3) return 0;
vector<int> dp(n + 1, 0);//dp[i]表示从nums[0]到nums[i]的等差子数组的个数
for (int i = 2; i < n; i++) {
if (nums[i] - nums[i - 1] == nums[i - 1] - nums[i - 2]) {
dp[i] = dp[i-1] + 1;
}
}
return accumulate(dp.begin(), dp.end(), 0);
}
};
或者,在更新dp时累加:
class Solution {
public:
int numberOfArithmeticSlices(vector<int>& nums) {
if (nums.size() < 3) return 0;
int n = nums.size();
vector<int> dp(n, 0);
int res = 0;
for (int i = 2; i < n; ++i) {
if (nums[i] - nums[i - 1] == nums[i - 1] - nums[i - 2]) {
dp[i] = dp[i - 1] + 1;
res += dp[i];
}
}
return res;
}
};
542. 01 矩阵

思路:从左上到右下,右下到左上,两次遍历矩阵,更新dp数组
class Solution {
public:
vector<vector<int>> updateMatrix(vector<vector<int>>& mat) {
if (mat.empty()) return {};
int n = mat.size(), m = mat[0].size();
vector<vector<int>> dp(n, vector<int>(m, INT_MAX - 1));
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
if (mat[i][j] == 0) {
dp[i][j] = 0;
} else {
if (j > 0) {
dp[i][j] = min(dp[i][j], dp[i][j - 1] + 1);
}
if (i > 0) {
dp[i][j] = min(dp[i][j], dp[i - 1][j] + 1);
}
}
}
}
for (int i = n - 1; i >= 0; i--) {
for (int j = m - 1; j >= 0; j--) {
if (mat[i][j] != 0) {
if (j < m - 1) {
dp[i][j] = min(dp[i][j], dp[i][j + 1] + 1);
}
if (i < n - 1) {
dp[i][j] = min(dp[i][j], dp[i + 1][j] + 1);
}
}
}
}
return dp;
}
};
221. 最大正方形


对于在矩阵内搜索正方形或长方形的题型,一种常见的做法是定义一个二维 dp 数组,其中** dp[i][j] **表示满足题目条件的、以 (i, j) 为右下角的正方形或者长方形的属性。
对于本题,则表示 以 (i, j) 为右下角的全由 1 构成的最大正方形面积。如果当前位置是 0,那么 dp[i][j] 即为 0;如果 当前位置是 1,我们假设 dp[i][j] = k2,其充分条件为 dp[i-1][j-1]、dp[i][j-1] 和 dp[i-1][j]的值必须 都不小于 (k k 1)2,否则 (i, j) 位置不可以构成一个边长为 k 的正方形。同理,如果这三个值中的 的最小值为 k k 1,则 (i, j) 位置一定且最大可以构成一个边长为 k 的正方形。
class Solution {
public:
int maximalSquare(vector<vector<char>>& matrix) {
if (matrix.empty() || matrix[0].empty())
return 0;
int m = matrix.size(), n = matrix[0].size(), max_side = 0;
vector<vector<int>> dp(m + 1, vector<int>(n + 1, 0));
for (int i = 1; i <= m; i++) {
for (int j = 1; j <= n; j++) {
if (matrix[i - 1][j - 1] == '1') {
dp[i][j] = min({dp[i - 1][j - 1], dp[i - 1][j], dp[i][j - 1]}) + 1;
}
max_side = max(max_side, dp[i][j] );
}
}
return max_side * max_side;
}
};
拓展