131. 分割回文串

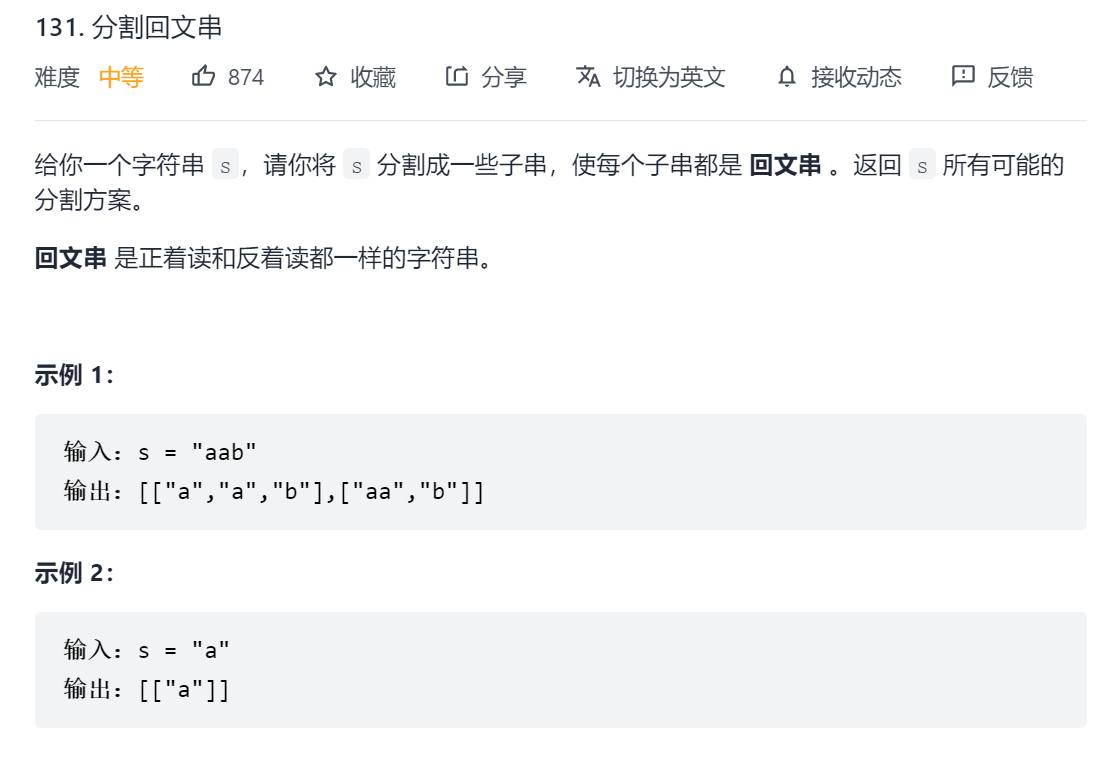
image.png

分割问题可以看作一种特殊的组合问题
image.png
如图，分割”aab”，横向选择不同的分割位置，纵向在余下的部分继续分割（递归的思想：分割字符串、子问题为分割子字符串）

回溯三部曲：

  1. 参数

参数是要分割的字符串、子串的起始位置

  1. void backtracking(const string& s, int startIndex) {
  1. 终止条件

如果切割线startIndex达到了字符串的末尾，那么分割完成，保存结果并返回

  1. if (startIndex >= s.size()) {
  2.         result.push_back(path);
  3.         return;
  4. }
  1. 单层搜索的逻辑

在for (int i = startIndex; i < s.size(); i++)循环中，我们 定义了起始位置startIndex，那么 [startIndex, i] 就是要截取的子串。
首先判断这个子串是不是回文，如果是回文，就加入在vector<string> path中，path用来记录切割过的回文子串。

  1. for (int i = startIndex; i < s.size(); i++) {
  2.     if (isPalindrome(s, startIndex, i)) {
  3.         path.push_back(s.substr(startIndex, i - startIndex + 1));
  4.     } else {
  5.         continue;
  6.     }
  7.     backtracking(s, i + 1);
  8.     path.pop_back();
  9. }

完整代码：

  1. class Solution {
  2. public:
  3.     vector<vector<string>> result;
  4.     vector<string> path;
  5.     // 双指针法判断是否为回文字符串
  6.     bool isPalindrome(const string& s, int start, int end) {
  7.         for (int i = start, j = end; i < j; i++, j--) {
  8.             if (s[i] != s[j]) return false;
  9.         }
  10.         return true;
  11.     }
  13.     void backtracking(const string& s, int startIndex) {
  14.         if (startIndex >= s.size()) {
  15.             result.push_back(path);
  16.             return;
  17.         }
  18.         for (int i = startIndex; i < s.size(); i++) {
  19.             if (isPalindrome(s, startIndex, i)) {
  20.                 path.push_back(s.substr(startIndex, i - startIndex + 1));
  21.             } else {
  22.                 continue;
  23.             }
  24.             backtracking(s, i + 1);
  25.             path.pop_back();
  26.         }
  27.     }
  30.     vector<vector<string>> partition(string s) {
  31.         backtracking(s, 0);
  32.         return result;
  33.     }
  34. };

93. 复原 IP 地址

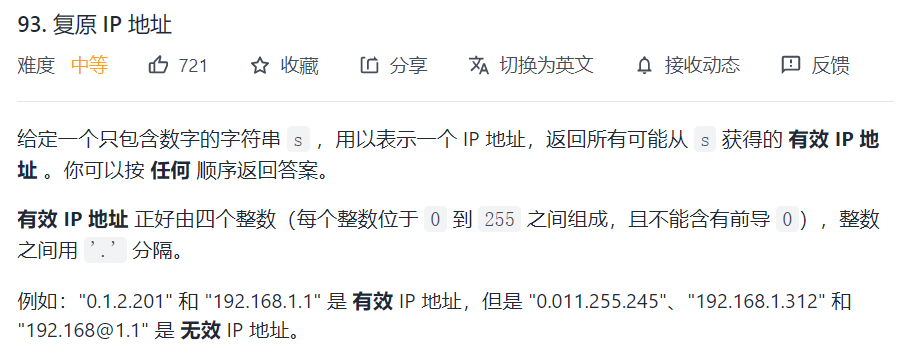
image.png
image.png

这还是一个分割问题，可以逐步分割，然后判断截取字段是否合法

用pointNum记录逗点数量，如果有3个，那么就已经分割为4段了

  1. if (pointNum == 3) { // 逗点数量为3时，分隔结束
  2.     // 判断第四段子字符串是否合法，如果合法就放进result中
  3.     if (isValid(s, startIndex, s.size() - 1)) {
  4.         result.push_back(s);
  5.     }
  6.     return;
  7. }
  1. 单层搜索的逻辑

与分割回文串那一题一样，for循环用于横向切割，然后递归处理剩下的部分
判断本层已经切割的部分是否合法，如果合法就保存结果，不合法就结束本层循环
image.png
然后就是递归和回溯的过程：
递归调用时，下一层递归的startIndex要从i+2开始（因为需要在字符串中加入了分隔符.），同时记录分割符的数量pointNum 要 +1。
回溯的时候，就将刚刚加入的分隔符. 删掉就可以了，pointNum也要-1。

  1. for (int i = startIndex; i < s.size(); i++) {
  2.     if (isValid(s, startIndex, i)) { // 判断 [startIndex,i] 这个区间的子串是否合法
  3.         s.insert(s.begin() + i + 1 , '.');  // 在i的后面插入一个逗点
  4.         pointNum++;
  5.         backtracking(s, i + 2, pointNum);   // 插入逗点之后下一个子串的起始位置为i+2
  6.         pointNum--;                         // 回溯
  7.         s.erase(s.begin() + i + 1);         // 回溯删掉逗点
  8.     } else break; // 不合法，直接结束本层循环
  9. }

判断数字是否合法：

  1.     bool isvalid(const string& s, int start, int end) {
  2.         if (start > end) return false;
  3.         // 以0开头的
  4.         if (s[start] == '0' && start != end) return false;
  5.         // 处理非数字和数值大于255的情况
  6.         int num = 0;
  7.         for (int i = start; i <= end; i++) {
  8.             if (s[i] > '9' || s[i] < '0') return fasle;
  9.             num = num * 10 + (s[i] - '0');
  10.             if (num > 255) return false
  12.         }
  13.         return true;
  14.     }

完整代码：

  1. class Solution {
  2. public:
  3.     vector<string> result;
  4.     void backtracking(string& s, int startIndex, int pointNum) {
  5.         // 终止条件
  6.         if (pointNum == 3) {
  7.             if (isValid(s, startIndex, s.size() - 1)) { // 第四段也合法，保存结果
  8.                 result.push_back(s);
  9.             }
  10.             return;
  11.         }
  12.         // 单层搜索的逻辑
  13.         for (int i = startIndex; i < s.size(); i++) {
  14.             if (isValid(s, startIndex, i)) {
  15.                 s.insert(s.begin() + i + 1, '.'); // 在分割的位置添加一个 .
  16.                 backtracking(s, i + 2, pointNum + 1); // pointNum 是形参，隐含回溯
  17.                 s.erase(s.begin() + i + 1); // 回溯， 把.删了
  18.             } else break;
  19.         }
  20.     }
  21.     bool isValid(const string& s, int start, int end) {
  22.         if (start > end) return false;
  23.         // 以0开头的
  24.         if (s[start] == '0' && start != end) return false;
  25.         // 处理非数字和数值大于255的情况
  26.         int num = 0;
  27.         for (int i = start; i <= end; i++) {
  28.             if (s[i] > '9' || s[i] < '0') 
  29.                 return false;
  30.             num = num * 10 + (s[i] - '0');
  31.             if (num > 255) 
  32.                 return false;
  34.         }
  35.         return true;
  36.     }
  38.     vector<string> restoreIpAddresses(string s) {
  39.         backtracking(s, 0, 0);
  40.         return result;
  41.     }
  42. };