- 剑指 Offer 16. 数值的整数次方
 ">剑指 Offer 16. 数值的整数次方
">剑指 Offer 16. 数值的整数次方
- 剑指 Offer 17. 打印从1到最大的n位数">(分治)剑指 Offer 17. 打印从1到最大的n位数
- 剑指 Offer 43. 1~n 整数中 1 出现的次数💦">剑指 Offer 43. 1~n 整数中 1 出现的次数💦
- 剑指 Offer 44. 数字序列中某一位的数字💦">剑指 Offer 44. 数字序列中某一位的数字💦
- 剑指 Offer 57 - II. 和为s的连续正数序列">剑指 Offer 57 - II. 和为s的连续正数序列
- 剑指 Offer 43. 1~n 整数中 1 出现的次数">剑指 Offer 43. 1~n 整数中 1 出现的次数
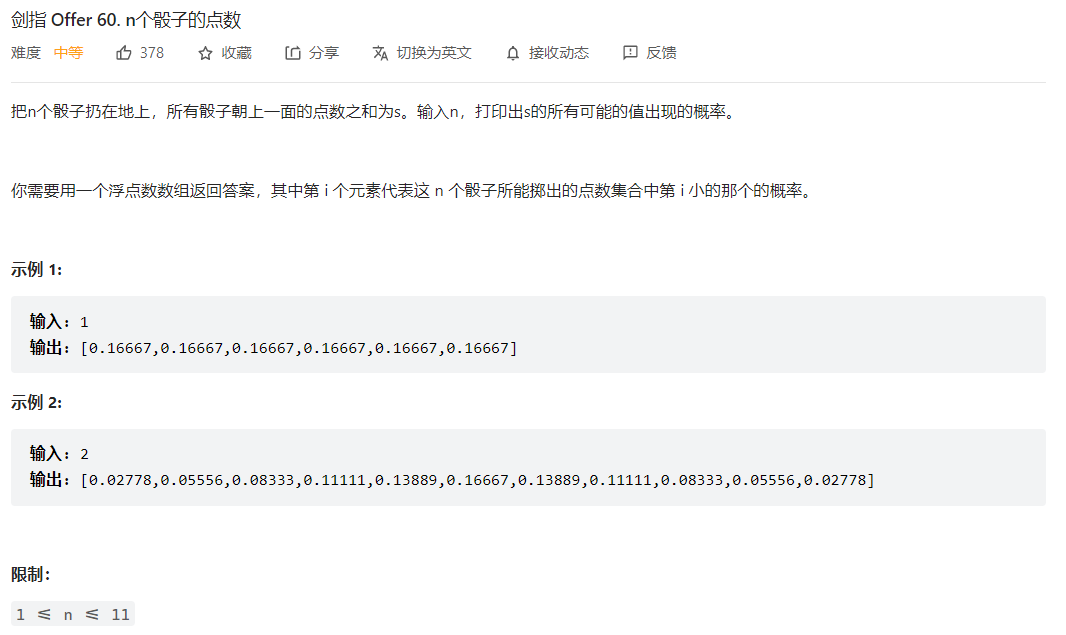
- 剑指 Offer 60. n个骰子的点数">剑指 Offer 60. n个骰子的点数
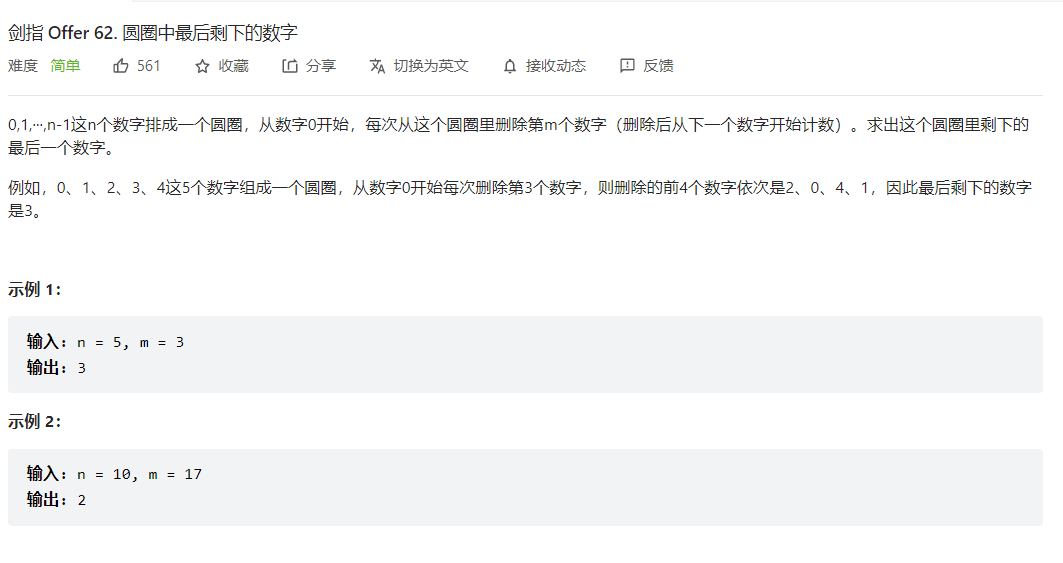
- 剑指 Offer 62. 圆圈中最后剩下的数字💦">剑指 Offer 62. 圆圈中最后剩下的数字💦
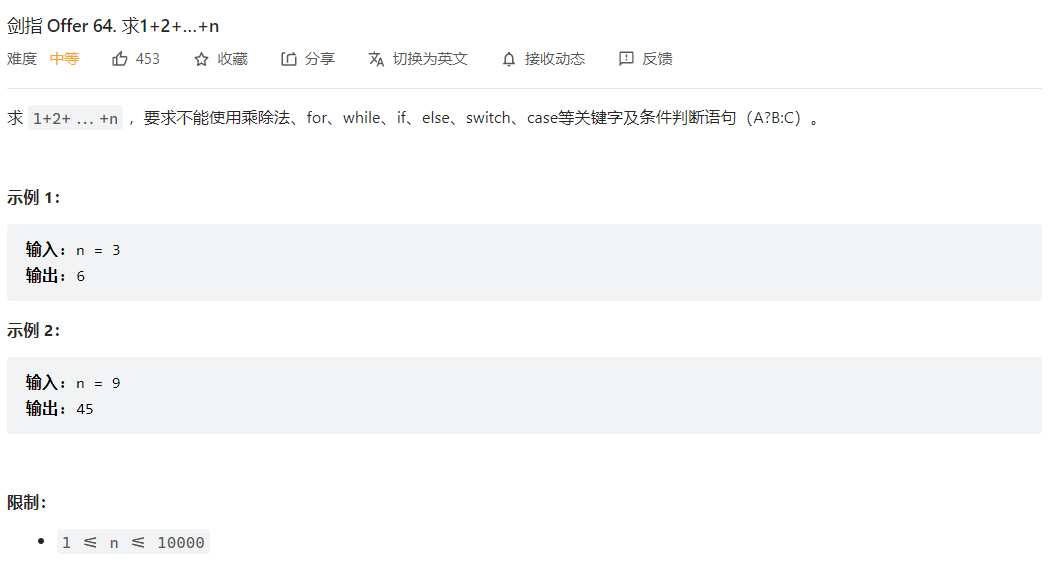
- 剑指 Offer 64. 求1+2+…+n">剑指 Offer 64. 求1+2+…+n
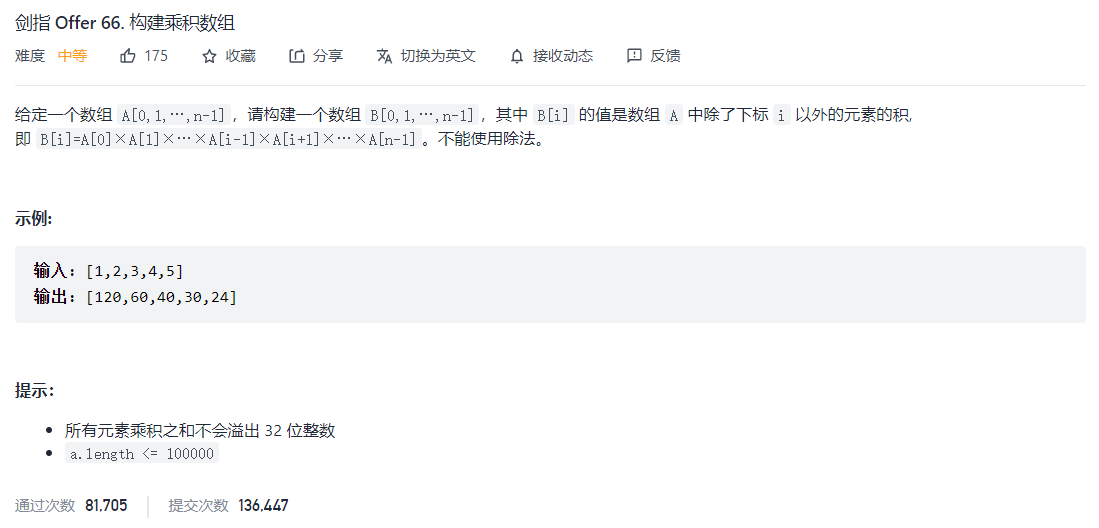
- 剑指 Offer 66. 构建乘积数组">剑指 Offer 66. 构建乘积数组
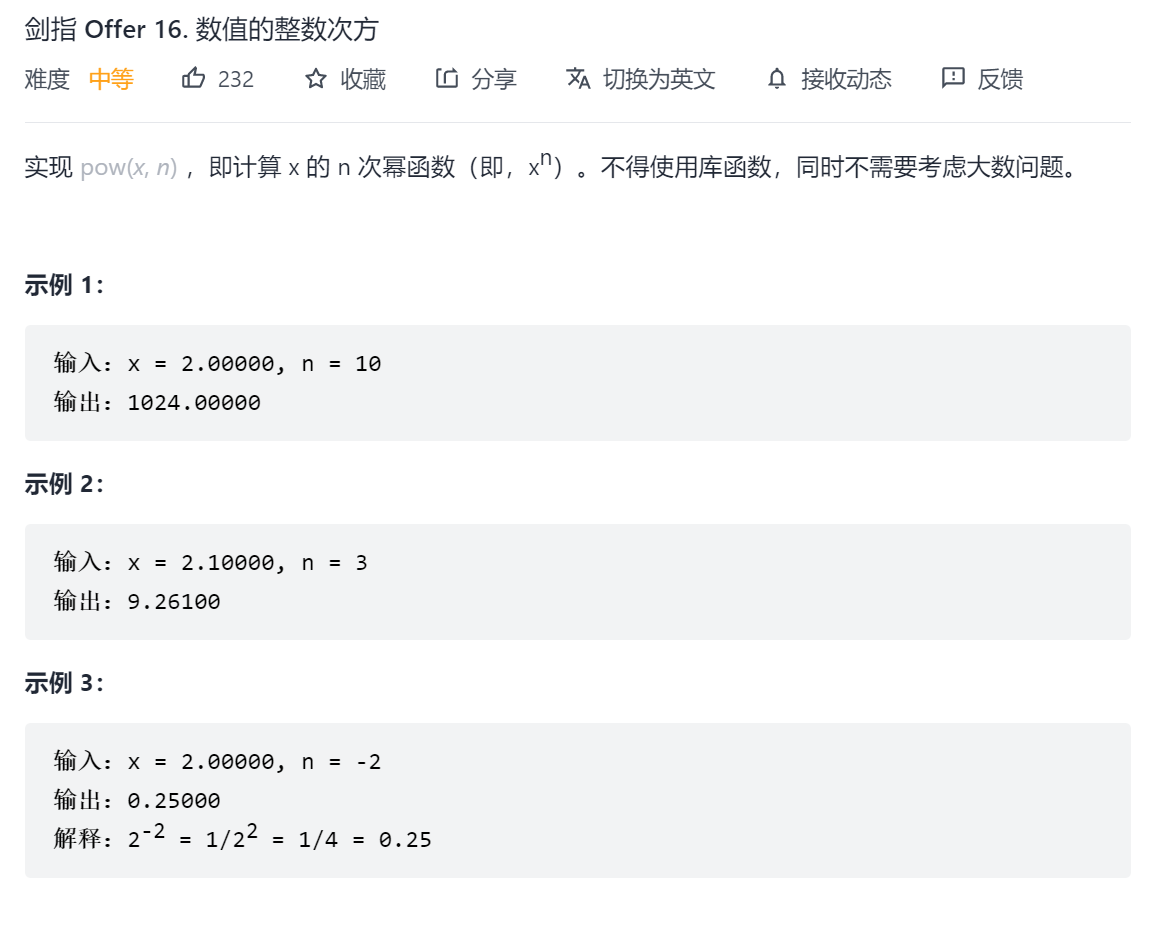
剑指 Offer 16. 数值的整数次方
递归(循环)法, 考虑0和负数的算法(超时)
class Solution {public:double myPow(double x, int n) {if (n == 0)return 1;else if (n > 0)return func(x, n);elsereturn 1 / func(x, -n);}double func(double x, int n) {double res = 1;for (int i = 0; i < n; i++) {res *= x;}return res;}};
class Solution {
public:
double pow(double x, int &n) {
if (n == 1)
return x;
return x * pow(x, --n);
}
double myPow(double x, int n) {
if (n > 0)
return pow(x, n);
else if (n == 0)
return 1;
else {
n *= -1;
return 1.0 / pow(x, n);
}
}
};
时间复杂度为O(n)
这个不能通过所有测试样例,会越界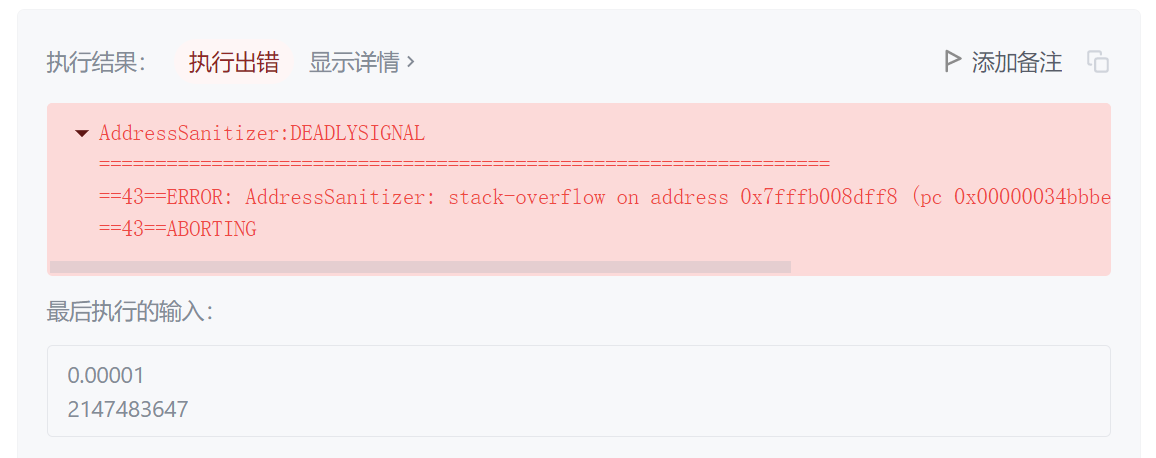
快速幂💦

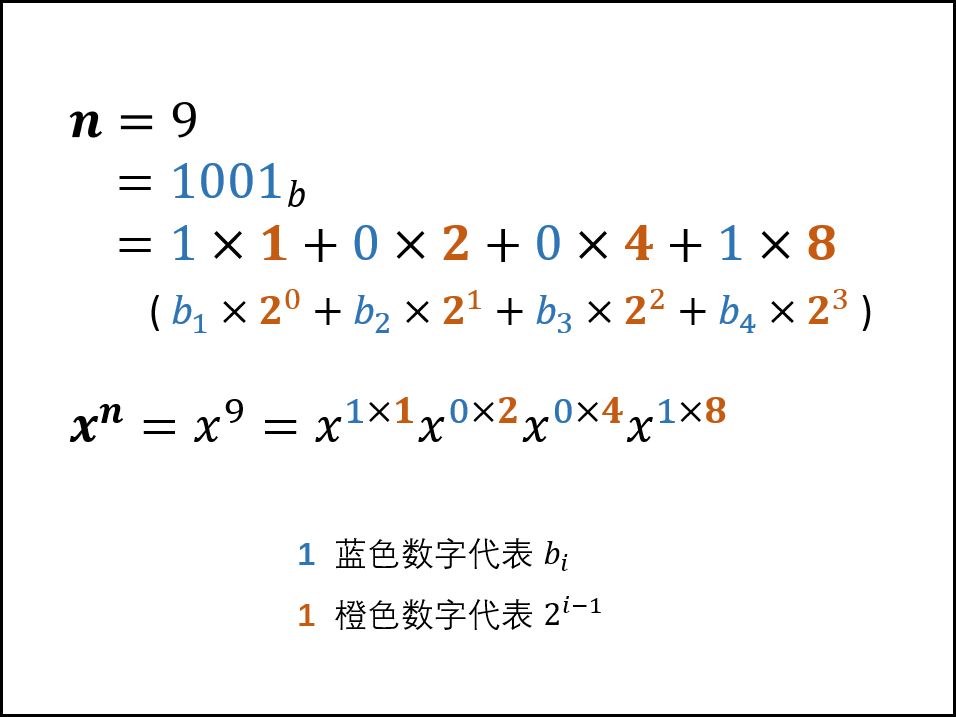



快速幂可以将时间复杂度降为O(logn)
class Solution {
public:
double myPow(double x, int n) {
if(x == 0) return 0;
long long b = n;
double res = 1.0;
if(b < 0) {
x = 1 / x;
b = -b;
}
while(b > 0) {
if((b & 1) == 1) // 如果对应位为1,那么就乘上x^(2^m)
res *= x;
x *= x; //
b >>= 1;
}
return res;
}
};
(分治)剑指 Offer 17. 打印从1到最大的n位数
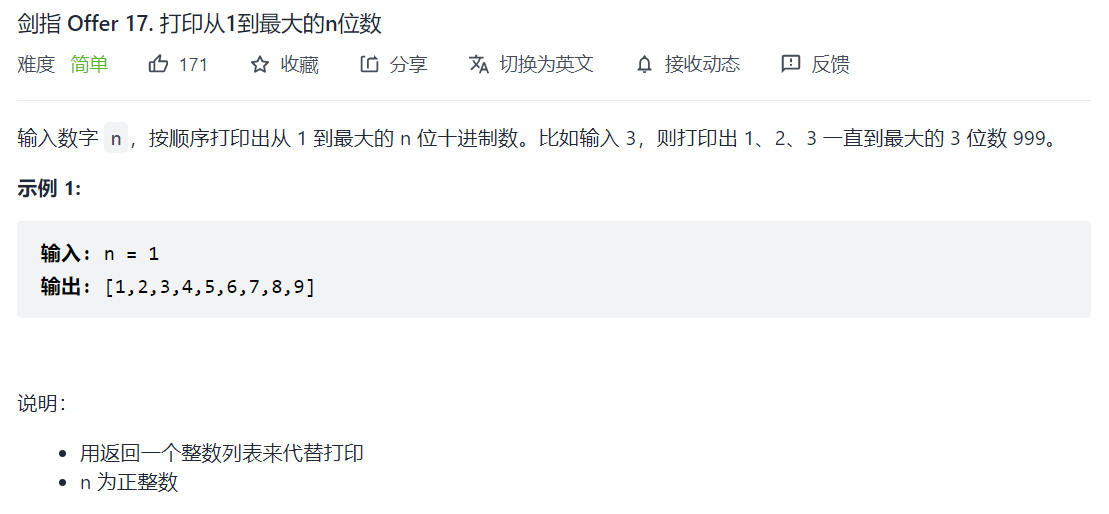
class Solution {
public:
vector<int> printNumbers(int n) {
int temp = pow(10, n);
vector<int> res;
for (int i = 1; i < temp; i++) {
res.push_back(i);
}
return res;
}
};
剑指 Offer 43. 1~n 整数中 1 出现的次数💦
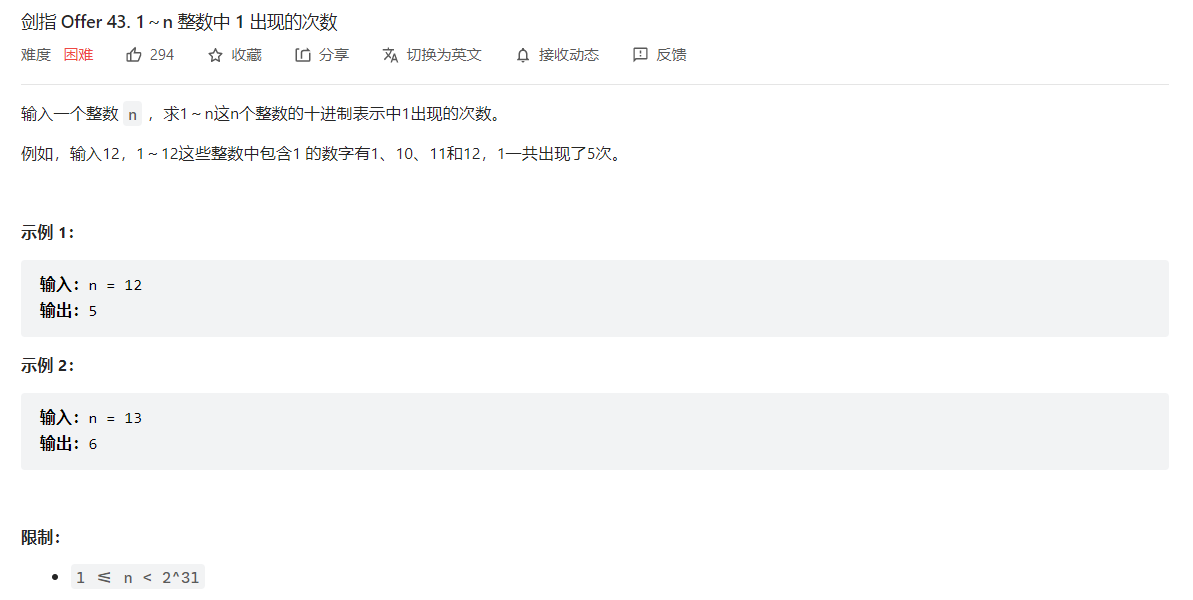
暴力解法可以对每个数字求1的个数,这里不多赘述
找数字规律
本体是找1的个数,而不是找某位为1的数字个数


class Solution {
public:
int countDigitOne(int n) {
long long digit = 1, res = 0;
// 初始化高位,和当前位,从个位开始处理
long long high = n / 10, cur = n % 10, low = 0;
while(high != 0 || cur != 0) {
if(cur == 0) res += high * digit;
else if(cur == 1) res += high * digit + low + 1;
else res += (high + 1) * digit;
low += cur * digit;
cur = high % 10;
high /= 10;
digit *= 10;
}
return res;
}
};
剑指 Offer 44. 数字序列中某一位的数字💦
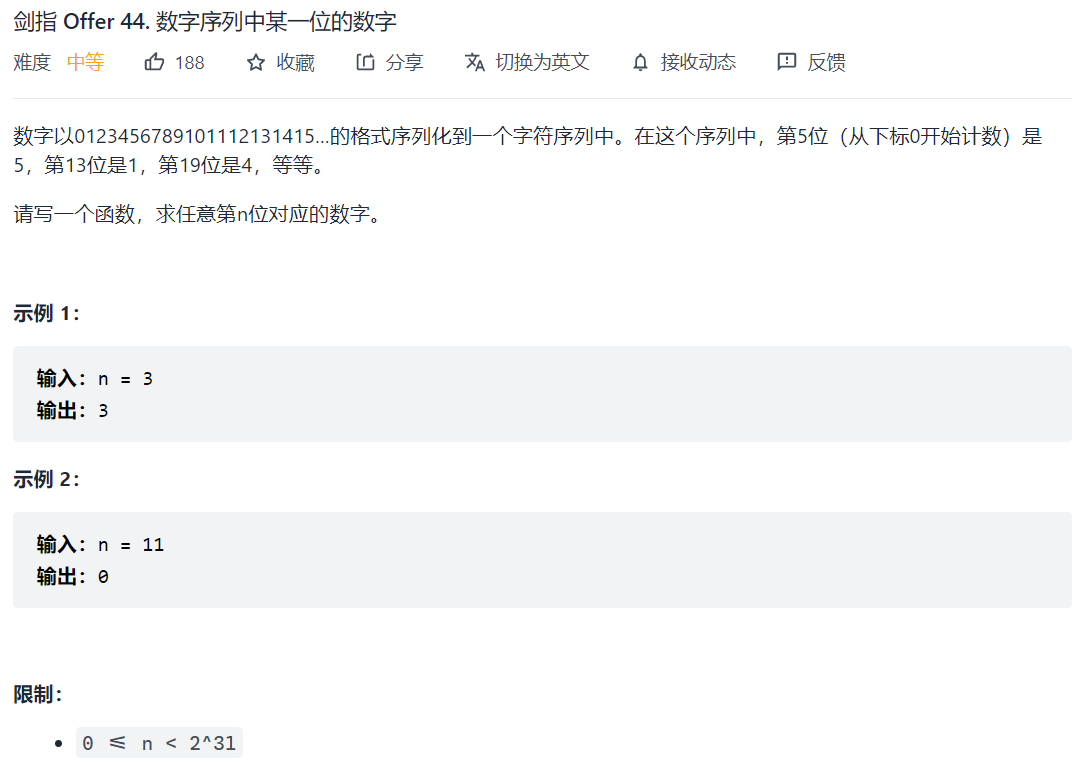
class Solution:
def findNthDigit(self, n: int) -> int:
digit, start, count = 1, 1, 9
while n > count: # 1.
n -= count
start *= 10
digit += 1
count = 9 * start * digit
num = start + (n - 1) // digit # 2.
return int(str(num)[(n - 1) % digit]) # 3.
剑指 Offer 57 - II. 和为s的连续正数序列
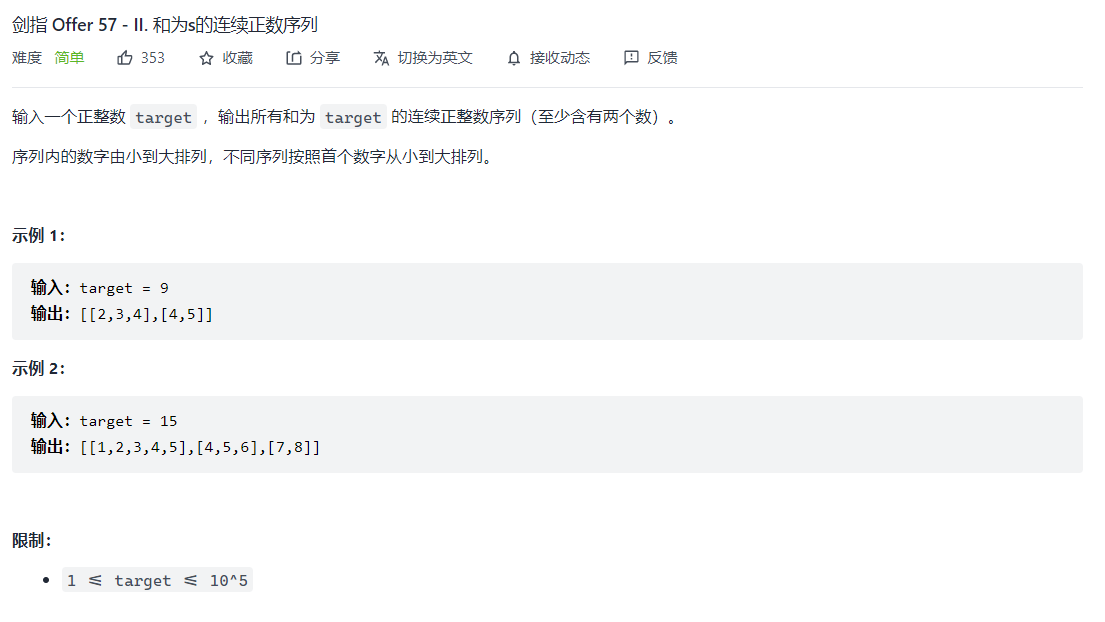
class Solution {
public:
vector<vector<int>> findContinuousSequence(int target) {
vector<vector<int>>vec;
vector<int> res;
for (int l = 1, r = 2; l < r;){
int sum = (l + r) * (r - l + 1) / 2;
if (sum == target) {
res.clear();
for (int i = l; i <= r; ++i) {
res.emplace_back(i);
}
vec.emplace_back(res);
l++;
} else if (sum < target) {
r++;
} else {
l++;
}
}
return vec;
}
};
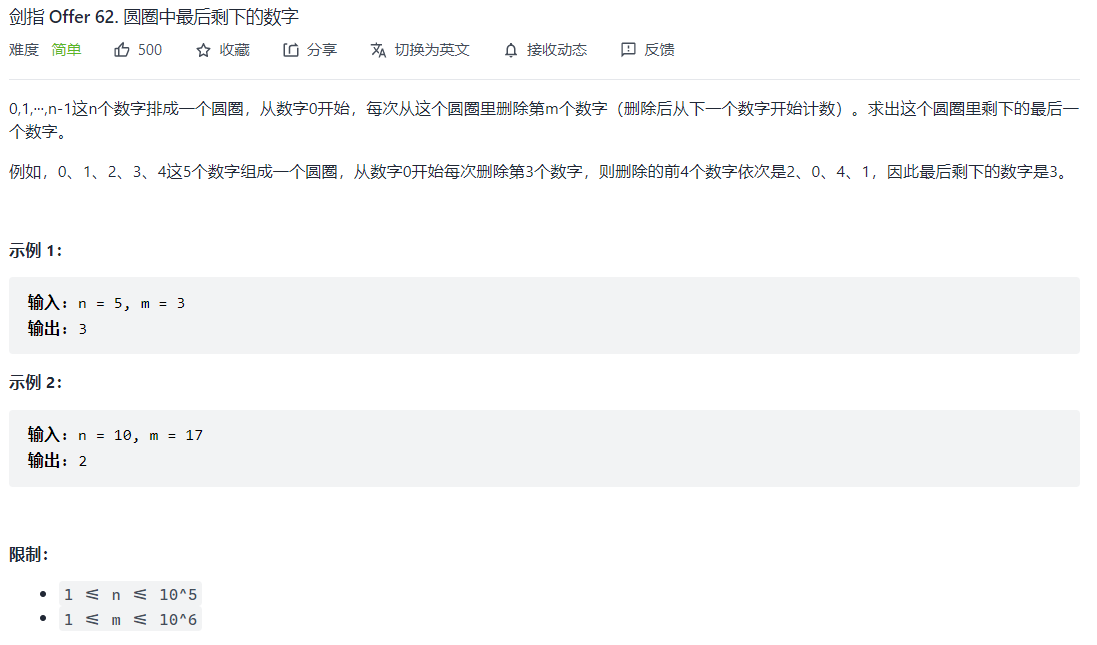
class Solution {
public:
int lastRemaining(int n, int m) {
int f = 0;
for (int i = 2; i != n + 1; ++i) {
f = (m + f) % i;
}
return f;
}
};
剑指 Offer 43. 1~n 整数中 1 出现的次数
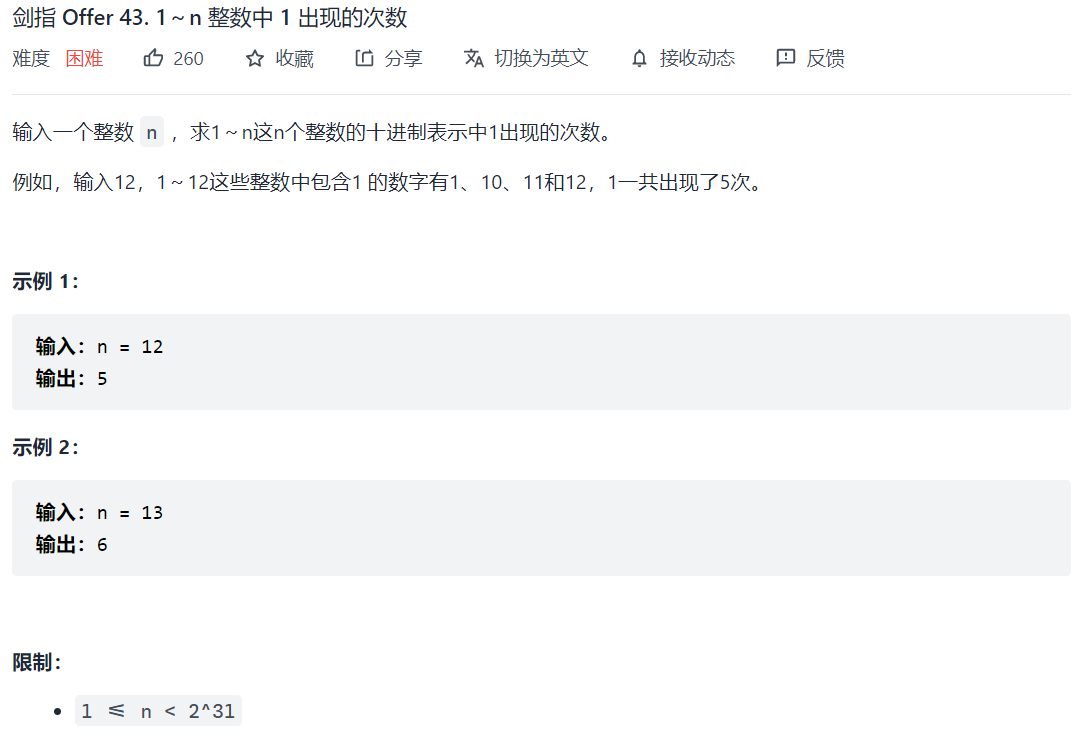
class Solution {
public:
int countDigitOne(int n) {
// mulk 表示 10^k
// 在下面的代码中,可以发现 k 并没有被直接使用到(都是使用 10^k)
// 但为了让代码看起来更加直观,这里保留了 k
long long mulk = 1;
int ans = 0;
for (int k = 0; n >= mulk; ++k) {
ans += (n / (mulk * 10)) * mulk + min(max(n % (mulk * 10) - mulk + 1, 0LL), mulk);
mulk *= 10;
}
return ans;
}
};
剑指 Offer 60. n个骰子的点数

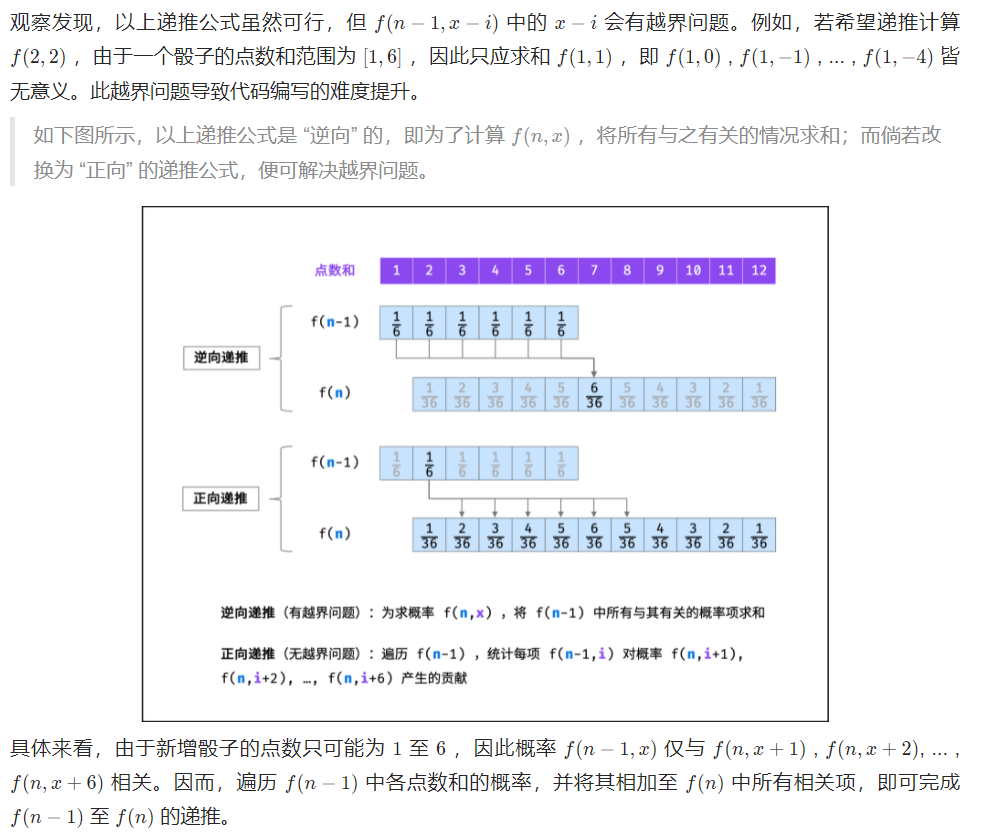
class Solution {
public:
vector<double> dicesProbability(int n) {
vector<double> dp(6, 1.0 / 6.0);
for (int i = 2; i <= n; i++) {
vector<double> tmp(5 * i + 1, 0);
for (int j = 0; j < dp.size(); j++) {
for (int k = 0; k < 6; k++) {
tmp[j + k] += dp[j] / 6.0;
}
}
dp = tmp;
}
return dp;
}
};
剑指 Offer 62. 圆圈中最后剩下的数字💦
class Solution {
public:
int lastRemaining(int n, int m) {
if (n == 1)
return 0;
int last = 0;
for (int i = 2; i <= n; ++i) {
last = (last + m) % i;
}
return last;
}
};
剑指 Offer 64. 求1+2+…+n
思路一
bool型变量占一个字节,因此创建一个 n _n + 1 大小的bool型二维数组,那么他的大小就是 n _* n + 1,再用右移位运算,完成除以二操作
class Solution {
public:
int sumNums(int n) {
bool temp[n][n + 1];
return sizeof(temp) >> 1;
}
};
思路二
逻辑与运算符,如果左边的表达式为0,那么将不会运算右边的表达式
可以根据这个特性来实现if else,然后用递归来处理循环
class Solution {
public:
int sumNums(int n) {
int res = n;
n && (res += sumNums(n - 1));
return res;
}
};
剑指 Offer 66. 构建乘积数组

class Solution {
public:
vector<int> constructArr(vector<int>& a) {
int n = a.size();
vector<int> b(n, 1);
// 计算下三角
for (int i = 1; i < n; ++i) {
b[i] = b[i - 1] * a[i - 1];
}
// 计算上三角
for (int i = n - 1, tmp = 1; i >= 0; --i) {
b[i] *= tmp;
tmp *= a[i];
}
return b;
}
};