20. 有效的括号
先来分析一下 这里有三种不匹配的情况,
- 第一种情况,字符串里左方向的括号多余了 ,所以不匹配。
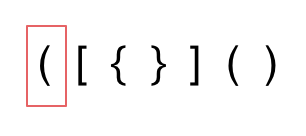
- 第二种情况,括号没有多余,但是 括号的类型没有匹配上。
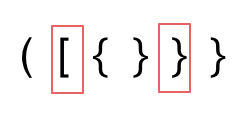
- 第三种情况,字符串里右方向的括号多余了,所以不匹配。
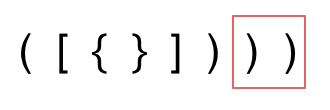
我们的代码只要覆盖了这三种不匹配的情况,就不会出问题,可以看出 动手之前分析好题目的重要性。
动画如下:
第一种情况:已经遍历完了字符串,但是栈不为空,说明有相应的左括号没有右括号来匹配,所以return false
第二种情况:遍历字符串匹配的过程中,发现栈里没有要匹配的字符。所以return false
第三种情况:遍历字符串匹配的过程中,栈已经为空了,没有匹配的字符了,说明右括号没有找到对应的左括号return false
那么什么时候说明左括号和右括号全都匹配了呢,就是字符串遍历完之后,栈是空的,就说明全都匹配了。
思路一
括号匹配,当然是使用栈了,扫描字符串,当遇到左括号时,将其压入栈中,遇到右括号时,如果栈空或者栈顶元素和此括号不匹配,则匹配失败,如果匹配成功,将栈顶元素弹出。当扫描完整个字符串,若栈空,则匹配成功,若栈不空,匹配失败
class Solution {public:bool isValid(string s) {int n = s.size();if (n % 2)return false;stack<char> stk;for(auto c : s) {if (c == '(' || c == '[' || c == '{')stk.push(c);else {//栈中没有左括号或者栈顶元素和括号不匹配时,匹配失败if (stk.empty())return false;char temp = stk.top();if (!((temp == '(' && c == ')') || (temp == '[' && c == ']') || (temp == '{' && c == '}')))return false;elsestk.pop();}}return stk.empty();}};
思路二
当遇到左括号时,将对应的右括号压入栈中,遇到右括号时,和栈顶元素比较,判断元素是否相同
这种实现起来要比左括号先入栈要简单一些
class Solution {
public:
bool isValid(string s) {
stack<int> st;
for (int i = 0; i < s.size(); i++) {
if (s[i] == '(') st.push(')');
else if (s[i] == '{') st.push('}');
else if (s[i] == '[') st.push(']');
// 第三种情况:遍历字符串匹配的过程中,栈已经为空了,没有匹配的字符了,说明右括号没有找到对应的左括号 return false
// 第二种情况:遍历字符串匹配的过程中,发现栈里没有我们要匹配的字符。所以return false
else if (st.empty() || st.top() != s[i]) return false;
else st.pop(); // st.top() 与 s[i]相等,栈弹出元素
}
// 第一种情况:此时我们已经遍历完了字符串,但是栈不为空,说明有相应的左括号没有右括号来匹配,所以return false,否则就return true
return st.empty();
}
};
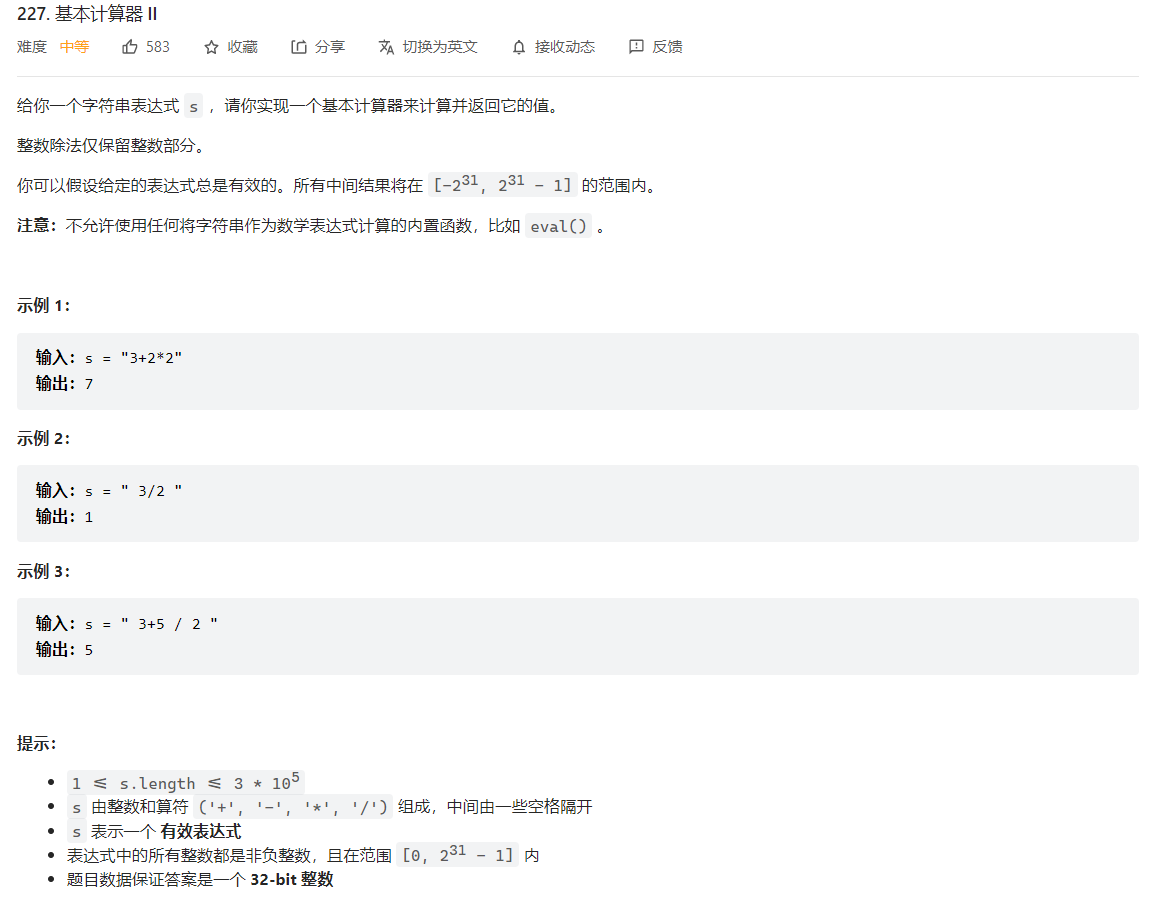
227. 基本计算器 II
class Solution {
public:
int calculate(string s) {
vector<int> st; // 用vector表示栈
char preSign = '+';
long long num = 0;
for (int i = 0; i < s.size(); i++) {
if (isdigit(s[i])) {
num = num * 10 + s[i] - '0';
}
if (!isdigit(s[i]) && s[i] != ' ' || i == s.size() - 1) { // 处理符号
if (preSign == '+') st.push_back(num);
else if (preSign == '-') st.push_back(-num);
else if (preSign == '*') st.back() *= num;
else st.back() /= num;
num = 0;
preSign = s[i];
}
}
return accumulate(st.begin(), st.end(), 0);
}
};
232. 用栈实现队列


思路
两个栈:
- 输入栈
- 输出栈
逻辑:
- 当有元素入队时:将元素压入输入栈
- 当有元素出队或者访问队头时:
- 若输出栈为空,将输入栈所有元素转入输出栈,然后弹出(访问)输出栈栈顶元素
- 若输出栈不为空,弹出(访问)输出栈栈顶元素
- 判空:若两个栈都为空,则队空
动画模拟:(代码随想录)
执行语句:
queue.push(1);
queue.push(2);
queue.pop(); 注意此时的输出栈的操作
queue.push(3);
queue.push(4);
queue.pop();
queue.pop();注意此时的输出栈的操作
queue.pop();
queue.empty();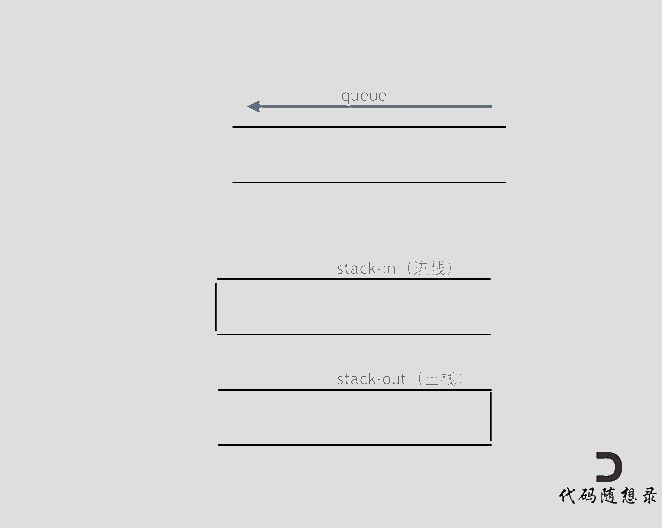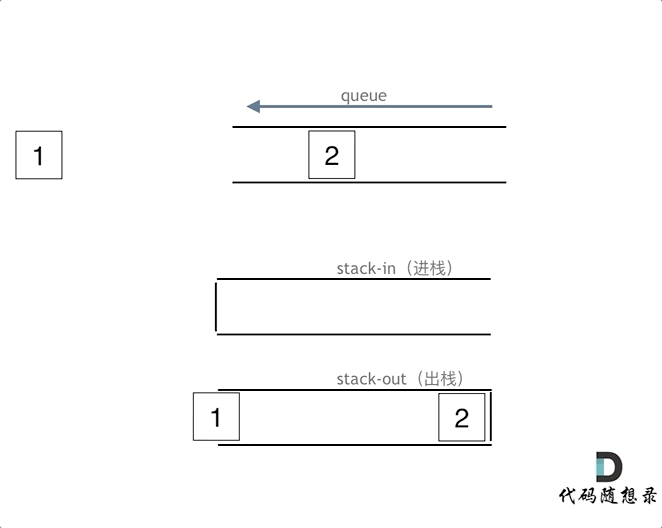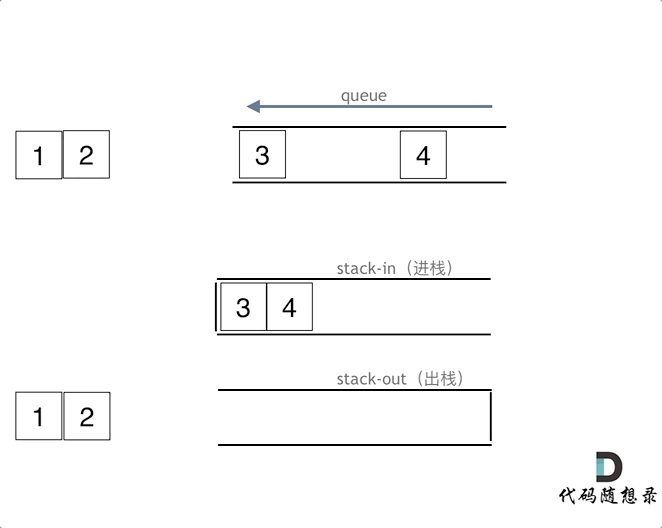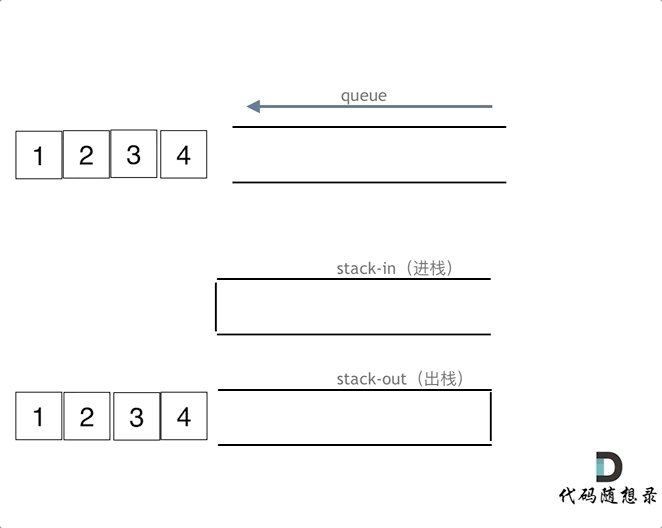
C++代码:
class MyQueue {
public:
MyQueue() {}
void push(int x) {
st1.push(x);
}
int pop() {
if (st2.empty()) {
while (!st1.empty()) {
st2.push(st1.top());
st1.pop();
}
}
int temp = st2.top();
st2.pop();
return temp;
}
int peek() {
if (st2.empty()) {
while (!st1.empty()) {
st2.push(st1.top());
st1.pop();
}
}
return st2.top();
}
bool empty() {
return st1.empty() && st2.empty();
}
stack<int> st1; // 用于入队
stack<int> st2; // 用于出队
};
时间复杂度分析:
入队:O(1)
出队:摊还复杂度 O(1),最坏情况下的时间复杂度 O(n)
在最坏情况下,s2 为空,算法需要从 s1 中弹出 n 个元素,然后再把这 n 个元素压入 s2,在这里n代表队列的大小。这个过程产生了 2n 步操作,时间复杂度为 O(n)。但当 s2 非空时,算法就只有 O(1) 的时间复杂度
225. 用队列实现栈
用两个队列实现
队列是先入先出,栈是后入先出,要用队列模拟栈,关键在于如何改变元素的输出顺序
用一个队列来存储元素,当需要访问栈顶元素(位于队尾)时,将除队尾外所有的元素移入另一个队列,访问后再将所有元素移动回第一个队列即可。
动画模拟:(代码随想录)
queue.push(1);
queue.push(2);
queue.pop(); // 注意弹出的操作
queue.push(3);
queue.push(4);
queue.pop(); // 注意弹出的操作
queue.pop();
queue.pop();
queue.empty();
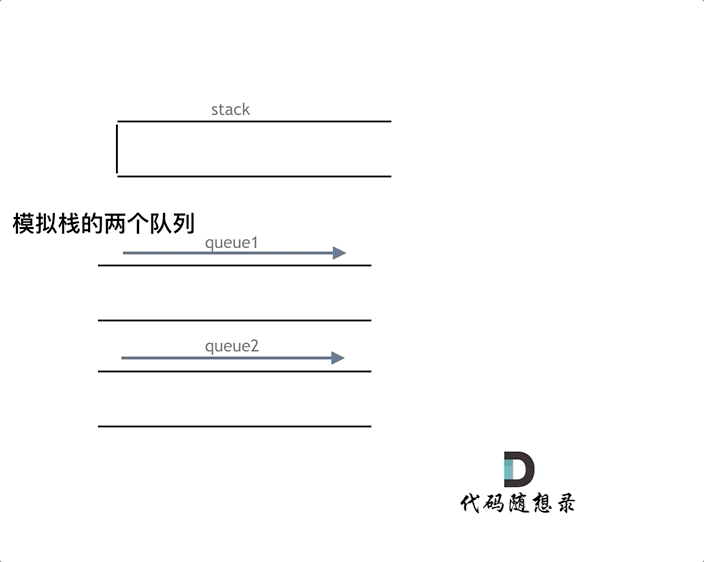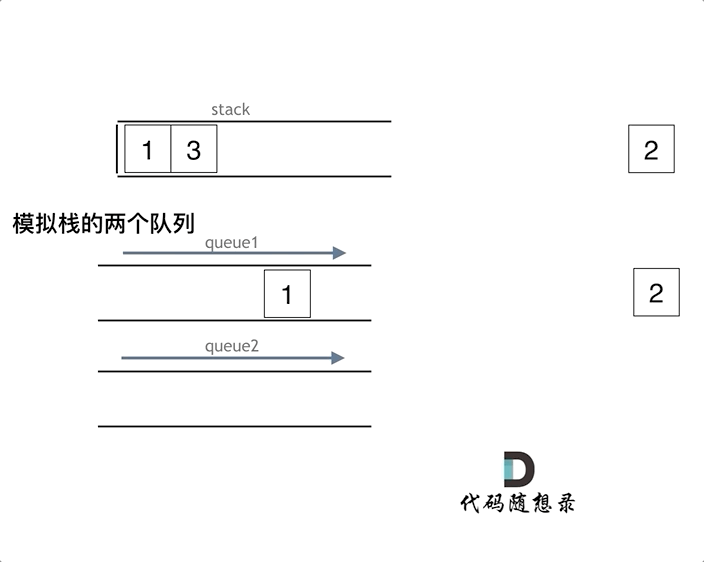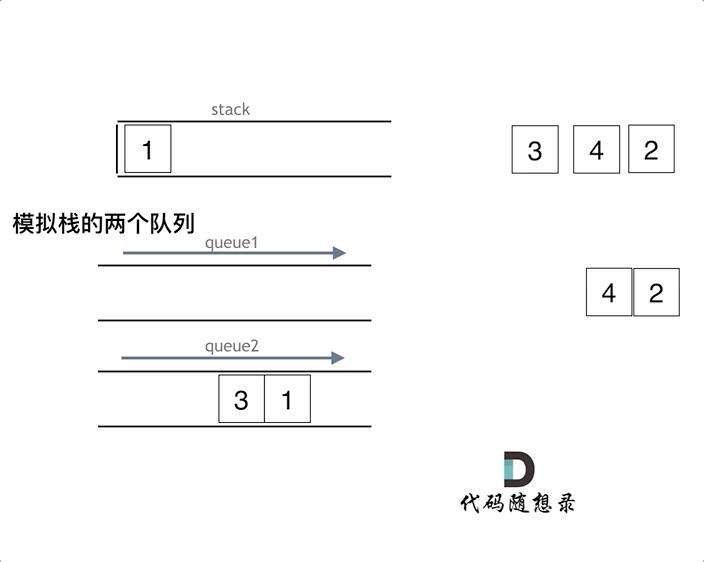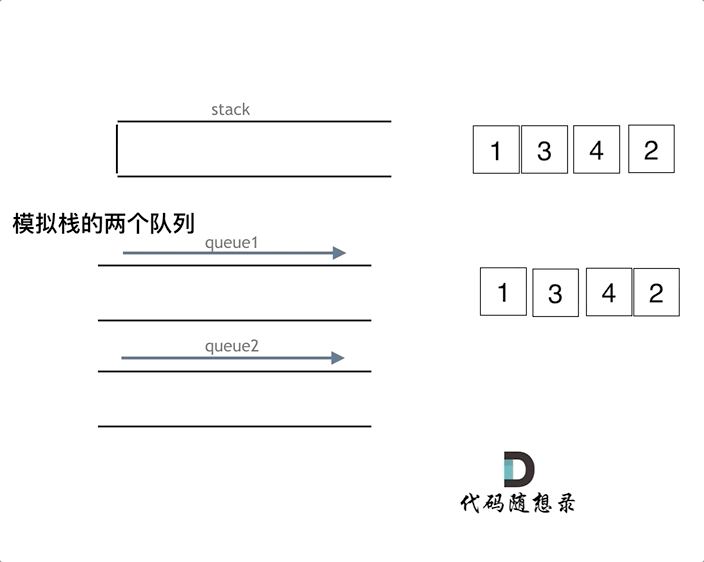
就是每次访问栈顶时,将队列的其他元素都移动到另一个队列,只留最后一个,使用完栈顶后,再将所有元素倒腾回来
class MyStack {
public:
MyStack() {
}
void push(int x) {
q1.push(x);
}
int pop() {
int res;
while (!q1.empty()) {
res = q1.front();
q1.pop();
if (q1.empty()) break;//如果是最后一个元素,要将其删除
q2.push(res);
}
while (!q2.empty()) {
q1.push(q2.front());
q2.pop();
}
return res;
}
int top() {
// return q1.back(); 也可以
int res;
while (!q1.empty()) {
res = q1.front();
q1.pop();
q2.push(res);
}
while (!q2.empty()) {
q1.push(q2.front());
q2.pop();
}
return res;
}
bool empty() {
return q1.empty();
}
queue<int> q1;
queue<int> q2;
};
/**
* Your MyStack object will be instantiated and called as such:
* MyStack* obj = new MyStack();
* obj->push(x);
* int param_2 = obj->pop();
* int param_3 = obj->top();
* bool param_4 = obj->empty();
*/
复杂度分析
- 时间复杂度:入队O(1), 出队O(n)
- 空间复杂度:O(n)
用一个队列实现
通过上面的分析发现,第二个队列实际上就是一个备份的作用,如果访问弹出栈顶元素时,直接将除队尾元素外的所有元素都进行重新入队操作,那么一个队列就可以实现栈了。
class MyStack {
public:
MyStack() {
}
void push(int x) {
q1.push(x);
}
int pop() {
int size = q1.size() - 1;
while (size--) {// 将所有元素重新加入队列
q1.push(q1.front());
q1.pop();
}
int res = q1.front();
q1.pop();
return res;
}
int top() {
return q1.back();
}
bool empty() {
return q1.empty();
}
queue<int> q1;
};
/**
* Your MyStack object will be instantiated and called as such:
* MyStack* obj = new MyStack();
* obj->push(x);
* int param_2 = obj->pop();
* int param_3 = obj->top();
* bool param_4 = obj->empty();
*/
附:摊还分析
摊还分析给出了所有操作的平均性能。摊还分析的核心在于,最坏情况下的操作一旦发生了一次,那么在未来很长一段时间都不会再次发生,这样就会均摊每次操作的代价。
来看下面这个例子,从一个空队列开始,依次执行下面这些操作:
单次出队操作最坏情况下的时间复杂度为O(n)。考虑到我们要做 n 次出队操作,如果我们用最坏情况下的时间复杂度来计算的话,那么所有操作的时间复杂度为 O(n^2)。
然而,在一系列的操作中,最坏情况不可能每次都发生,可能一些操作代价很小,另一些代价很高。因此,如果用传统的最坏情况分析,那么给出的时间复杂度是远远大于实际的复杂度的。例如,在一个动态数组里面只有一些插入操作需要花费线性的时间,而其余的一些插入操作只需花费常量的时间。
在上面的例子中,出队操作最多可以执行的次数跟它之前执行过入队操作的次数有关。虽然一次出队操作代价可能很大,但是每 n 次入队才能产生这么一次代价为 n 的出队操作。因此所有操作的总时间复杂度为:n(所有的入队操作产生) + 2 * n(第一次出队操作产生) + n - 1(剩下的出队操作产生), 所以实际时间复杂度为 O(2*n)。于是我们可以得到每次操作的平均时间复杂度为 O(2n/2n)=O(1)。
1047. 删除字符串中的所有相邻重复项
本题要删除相邻相同元素,其实也是匹配问题,相同左元素相当于左括号,相同右元素就是相当于右括号,匹配上了就删除。
那么再来看一下本题:可以把字符串顺序放到一个栈中,然后如果相同的话 栈就弹出,这样最后栈里剩下的元素都是相邻不相同的元素了。
从栈中弹出剩余元素,此时是字符串ac,因为从栈里弹出的元素是倒叙的,可以对字符串进行翻转,或者在扫描入栈的时候,从字符串的最后一个字符串往前扫描
字符串反转版本
class Solution { public: string removeDuplicates(string S) { stack<char> st; for (char s : S) { if (st.empty() || s != st.top()) { st.push(s); } else { st.pop(); // s 与 st.top()相等的情况 } } string result = ""; while (!st.empty()) { // 将栈中元素放到result字符串汇总 result += st.top(); st.pop(); } reverse (result.begin(), result.end()); // 此时字符串需要反转一下 return result; } };反向扫描版本
class Solution { public: string removeDuplicates(string s) { stack<char> st; for (int i = s.size() - 1; i >= 0; --i) { if (st.empty() || st.top() != s[i]) { st.push(s[i]); } else { st.pop(); } } string res; while (!st.empty()) { res.push_back(st.top()); st.pop(); } return res; } };
当然还可以用字符串代替栈,这样可以不用栈转换为字符串的操作
class Solution {
public:
string removeDuplicates(string s) {
string res;
for (auto c : s) {
if (res.empty() || res.back() != c) {
res.push_back(c);
} else {
res.pop_back();
}
}
return res;
}
};
复杂度分析
- 时间复杂度:O(n)O(n),其中 nn 是字符串的长度。我们只需要遍历该字符串一次。
- 空间复杂度:O(n)O(n) 或 O(1)O(1),取决于使用的语言提供的字符串类是否提供了类似「入栈」和「出栈」的接口。注意返回值不计入空间复杂度。
150. 逆波兰表达式求值

思路
和消除字符串中连续的重复元素类似,不过这次不是成对消除,而是进行运算
使用栈,扫描tokens:
- 如果是数字,入栈
- 如果是运算符,取出栈顶两个元素,然后做四则运算,将结果压入堆栈
最后返回栈顶元素即可
注:可以自定义string转换为整数的函数,C++中可以用stoi将string转换为int类型
class Solution {
public:
int evalRPN(vector<string>& tokens) {
stack<int> st;
for (auto &str: tokens) {
int num1, num2;
if (str == "+") {
num1 = st.top(); st.pop();
num2 = st.top(); st.pop();
st.push(num1 + num2);
} else if (str == "-") {
num1 = st.top(); st.pop();
num2 = st.top(); st.pop();
st.push(num2 - num1);
} else if (str == "*") {
num1 = st.top(); st.pop();
num2 = st.top(); st.pop();
st.push(num1 * num2);
} else if (str == "/") {
num1 = st.top(); st.pop();
num2 = st.top(); st.pop();
st.push(num2 / num1);
} else {
st.push(stoi(str));
}
}
return st.top();
}
};
复杂度分析
时间复杂度:O(n),其中 n是数组tokens 的长度。需要遍历数组 tokens 一次,计算逆波兰表达式的值。
空间复杂度:O(n),其中 nn 是数组 tokens 的长度。使用栈存储计算过程中的数,栈内元素个数不会超过逆波兰表达式的长度
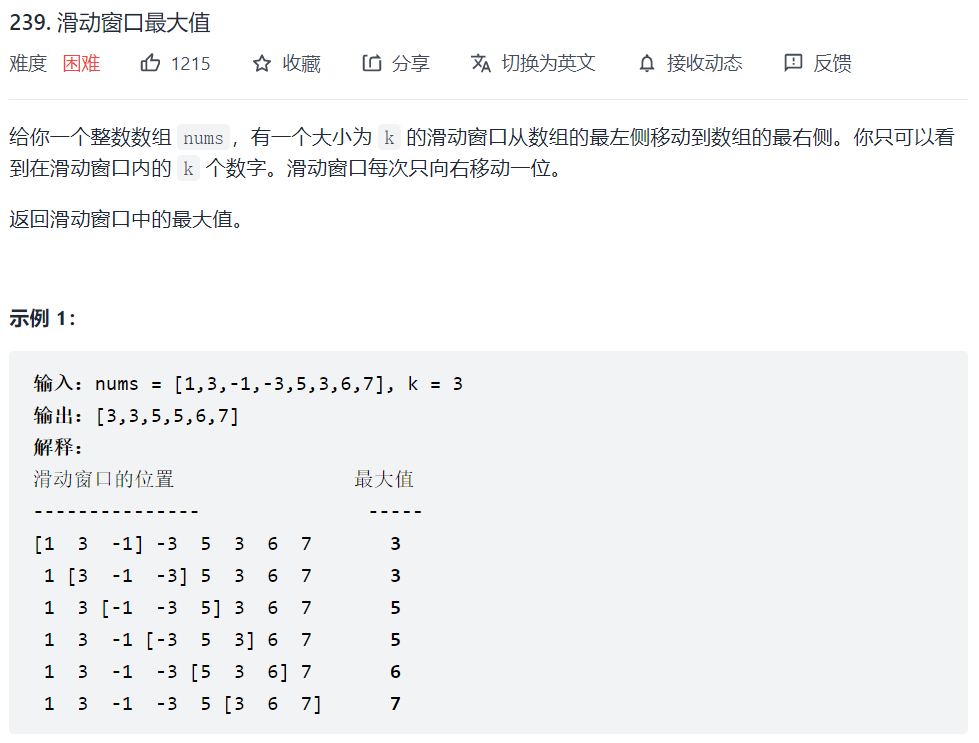
239. 滑动窗口最大值
思路一:暴力,超时
首先想到的是暴力解法,逐个窗口扫描取最大值,时间复杂度为O(kN),k是窗口大小,N是数组长度
class Solution {
public:
vector<int> maxSlidingWindow(vector<int>& nums, int k) {
vector<int> res;
for (int i = 0; i < nums.size() - k + 1; i++) {
res.push_back(findMax(nums, i, i + k));
}
return res;
}
int findMax(vector<int> nums, int begin, int end) {
int max = nums[begin];
for (int i = begin + 1; i < end; i++)
max = max < nums[i] ? nums[i] : max;
return max;
}
};
但是当提交后,发现果然不出所料,超出时间限制
因此暴力法对于此题不可取。
思路二:优先队列
对于「最大值」,我们可以想到一种非常合适的数据结构,那就是优先队列(堆),其中的大根堆可以帮助我们实时维护一系列元素中的最大值。
对于本题而言,初始时,我们将数组 nums 的前 k 个元素放入优先队列中。每当向右移动窗口时,要判断堆顶元素是不是要被移除,如果堆顶元素的下标不在窗口中,就把它移除。移除后,把一个新的元素放入优先队列中,此时堆顶的元素就是堆中所有元素的最大值。
为了方便判断堆顶元素与滑动窗口的位置关系,我们可以在优先队列中存储二元组 (num,index),表示元素 num 在数组中的下标为 index。
class Solution {
public:
vector<int> maxSlidingWindow(vector<int>& nums, int k) {
priority_queue<pair<int, int>> pq; // 值,索引
vector<int> res;
for (int i = 0; i < nums.size(); i++) {
pq.push({nums[i], i});
while (pq.top().second <= i - k) pq.pop();
if (i >= k - 1) res.push_back(pq.top().first);
}
return res;
}
};
复杂度分析
- 时间复杂度:O(nlogn),其中 n 是数组 nums 的长度。在最坏情况下,数组 nums 中的元素单调递增,那么最终优先队列中包含了所有元素,没有元素被移除。由于将一个元素放入优先队列的时间复杂度为 O(logn),因此总时间复杂度为 O(nlogn)。
- 空间复杂度:O(n),即为优先队列需要使用的空间。这里所有的空间复杂度分析都不考虑返回的答案需要的 O(n) 空间,只计算额外的空间使用
思路三:单调双端队列
假如有两个下标,i < j,并且 nums[i] < nums[j],在滑动窗口的过程中,如果i在窗口中,因为 i < j,那么j也一定在窗口中,由于 nums[i] < nums[j],nums[i]一定不会是窗口的最大值,此时,可以将nums[i]从窗口中删除
那么维护一个双端队列,保证从队尾到队头单调不减,这样可以始终保证队头元素为窗口的最大值,滑动窗口的过程中,向队尾添加元素时,将队尾元素弹出直到队尾元素大于等于要添加的元素为止(这个要添加的元素就是上面提到的nums[j],有它在,被弹出的元素不会是窗口的最大值),保存窗口最大值之前,将不在窗口中的队头元素删除。
为了便于操作,队列中存储数组的下标
class Solution {
public:
vector<int> maxSlidingWindow(vector<int>& nums, int k) {
deque<int> dq;
vector<int> res;
for (int i = 0; i < nums.size(); i++) {
while (!dq.empty() && nums[dq.back()] < nums[i]) dq.pop_back();
dq.push_back(i);
while (dq.front() <= i - k) dq.pop_front();
if (i >= k - 1) res.push_back(nums[dq.front()]);
}
return res;
}
};
复杂度分析:
- 时间复杂度:每一个下标恰好被放入队列一次,并且最多被弹出队列一次,因此时间复杂度为 O(n)。
- 空间复杂度:需要维护一个单调队,空间复杂度为O(k)
347. 前 K 个高频元素
思路一:堆 priority_queue
大顶堆
一般看到前k个什么什么,会想到利用快速排序或者堆。
对于这道题,输出前k高频元素,那么首先肯定要统计每个元素的频数,可以用map来进行统计,然后按照频数建立大顶堆,C++可以使用priority_queue,建好了堆输出k次堆顶就好了class Solution { public: vector<int> topKFrequent(vector<int>& nums, int k) { map<int, int> m; vector<int> res; for (auto num : nums) { m[num]++; } priority_queue<pair<int, int>> pq; for (auto p : m) { pq.emplace(p.second, p.first); } while(k--) { res.push_back(pq.top().second); pq.pop(); } return res; } };
小顶堆
用大顶堆可以依次弹出k的元素,当然也以用小顶堆,每次从小顶堆弹出的元素,是频数最小的,所以,可以维护一个大小为k的小顶堆,想堆中添加元素,超出k个时,将最小的弹出,最后剩下的k个元素就是前k个高频元素。
priority_queue默认是大顶堆,因此可以重载函数调用运算符()来改为小顶堆
C++代码:typedef pair<int, int> pii; class Solution { public: vector<int> topKFrequent(vector<int>& nums, int k) { unordered_map<int, int> um; for (auto num: nums) { ++um[num]; } priority_queue<pii, vector<pii>, greater<pii>> pq; // 小顶堆,堆头是频率小的元素 for (auto p: um) { pq.emplace(p.second, p.first); if (pq.size() > k) { // 元素数量超过k个,弹出最小值 pq.pop(); } } vector<int> res; for (int i = 0; i < k; ++i) { res.push_back(pq.top().second); pq.pop(); } return res; } };
复杂度分析:
时间复杂度:O(Nlogk),其中 N 为数组的长度。我们首先遍历原数组,并使用哈希表记录出现次数,每个元素需要 O(1) 的时间,共需 O(N) 的时间。随后,我们遍历「出现次数数组」,由于堆的大小至多为 k,因此每次堆操作需要 O(logk) 的时间,共需 O(Nlogk) 的时间。二者之和为 O(Nlogk)。
空间复杂度:O(N)。哈希表的大小为O(N),而堆的大小为O(k),共计为O(N)。
思路二:基于快速排序
思路与算法
我们可以使用基于快速排序的方法,求出「出现次数数组」的前 k 大的值。
在对数组 做快速排序的过程中,我们首先将数组划分为两个部分
与
,并使得
中的每一个值都不超过
,且
中的每一个值都大于
。
于是,我们根据 kk 与左侧子数组 的长度(为
)的大小关系:
如果 ,则数组
前 kk 大的值,就等于子数组
前 k 大的值。
否则,数组 前 k 大的值,就等于左侧子数组全部元素,加上右侧子数组
中前
大的值。
原版的快速排序算法的平均时间复杂度为 O(N\log N)。我们的算法中,每次只需在其中的一个分支递归即可,因此算法的平均时间复杂度降为 O(N)。
class Solution {
public:
void qsort(vector<pair<int, int>>& v, int start, int end, vector<int>& ret, int k) {
int picked = rand() % (end - start + 1) + start;
swap(v[picked], v[start]);
int pivot = v[start].second;
int index = start;
for (int i = start + 1; i <= end; i++) {
if (v[i].second >= pivot) {
swap(v[index + 1], v[i]);
index++;
}
}
swap(v[start], v[index]);
if (k <= index - start) {
qsort(v, start, index - 1, ret, k);
} else {
for (int i = start; i <= index; i++) {
ret.push_back(v[i].first);
}
if (k > index - start + 1) {
qsort(v, index + 1, end, ret, k - (index - start + 1));
}
}
}
vector<int> topKFrequent(vector<int>& nums, int k) {
unordered_map<int, int> occurrences;
for (auto& v: nums) {
occurrences[v]++;
}
vector<pair<int, int>> values;
for (auto& kv: occurrences) {
values.push_back(kv);
}
vector<int> ret;
qsort(values, 0, values.size() - 1, ret, k);
return ret;
}
};
复杂度分析
时间复杂度:O(N^2),其中 NN 为数组的长度。
设处理长度为 N 的数组的时间复杂度为 f(N)。由于处理的过程包括一次遍历和一次子分支的递归,最好情况下,有 f(N) = O(N) + f(N/2),根据 主定理,能够得到 f(N) = O(N)。
最坏情况下,每次取的中枢数组的元素都位于数组的两端,时间复杂度退化为 O(N^2)。
但由于我们在每次递归的开始会先随机选取中枢元素,故出现最坏情况的概率很低。平均情况下,时间复杂度为 O(N)。
空间复杂度:O(N)。哈希表的大小为 O(N),用于排序的数组的大小也为 O(N),快速排序的空间复杂度最好情况为 O(\log N),最坏情况为 O(N)。