剑指 Offer 09. 用两个栈实现队列

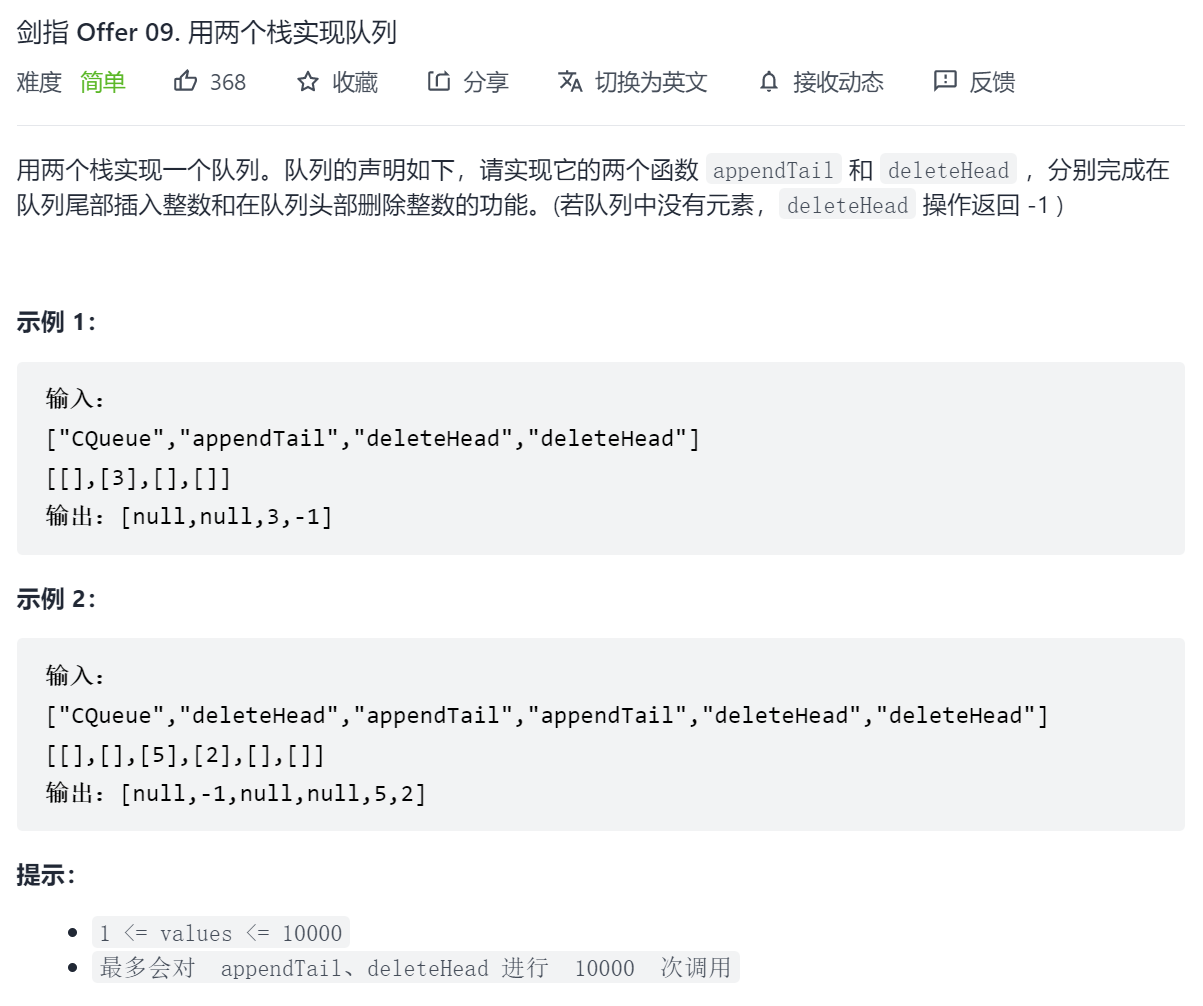
image.png

思路很简单，栈1用来进队，栈2用来出队
入队操作：

  • 将元素压入栈1

出队操作：

  • 如果两个栈都空，那么返回-1
  • 判断栈2是否为空：
    • 空：将栈1中的所有元素导入栈2，返回栈2的栈顶元素并弹出
    • 不空：返回栈2的栈顶元素并弹出
  1. class CQueue {
  2. public:
  3.     CQueue() {}
  5.     void appendTail(int value) {
  6.         st1.push(value);
  7.     }
  9.     int deleteHead() {
  10.         if (st2.empty() && st1.empty())
  11.             return -1;
  12.         if (st2.empty()) {
  13.             while (!st1.empty()) {
  14.                 st2.push(st1.top());
  15.                 st1.pop();
  16.             }
  17.         }
  18.         int temp = st2.top();
  19.         st2.pop();
  20.         return temp;
  21.     }
  22.     stack<int> st1;
  23.     stack<int> st2; 
  24. };
  26. /**
  27.  * Your CQueue object will be instantiated and called as such:
  28.  * CQueue* obj = new CQueue();
  29.  * obj->appendTail(value);
  30.  * int param_2 = obj->deleteHead();
  31.  */

剑指 Offer 30. 包含min函数的栈

image.png

思路一：单调栈辅助

因为要求维护栈中的最小值，并且要求min函数的时间复杂度为O(1)，那么可以用一个单调栈来维护栈中的最小元素，单调栈的栈顶始终是栈的最小元素

push：

  • st1正常操作
  • 如果st2的栈顶元素大于等于x（取等号是因为可能有两个相同的最小值），那么将x压入栈2，相当于更新最小值（st2的栈顶），否则不操作

pop：

  • 如果两个栈的栈顶相同，弹出的是最小值，此时需要将两个栈的栈顶都弹出，否则只弹出st1的栈顶元素

top：

  • st1.top()

min:

  • st2.top()
  1. class MinStack {
  2. public:
  3.     /** initialize your data structure here. */
  4.     MinStack() {}
  6.     void push(int x) {
  7.         st1.push(x);
  8.         if (st2.empty() || st2.top() >= x) {
  9.             st2.push(x);
  10.         }
  11.     }
  13.     void pop() {
  14.         if (st2.top() == st1.top())
  15.             st2.pop();
  16.         st1.pop();
  17.     }
  19.     int top() {
  20.         return st1.top();
  21.     }
  23.     int min() {
  24.         return st2.top();
  25.     }
  27.     stack<int> st1;
  28.     stack<int> st2; // 单调栈，栈顶是最小元素
  29. };
  31. /**
  32.  * Your MinStack object will be instantiated and called as such:
  33.  * MinStack* obj = new MinStack();
  34.  * obj->push(x);
  35.  * obj->pop();
  36.  * int param_3 = obj->top();
  37.  * int param_4 = obj->min();
  38.  */

思路二：保存两个值

1.先存x，再存最小值

每当push时，先将x放入，在存储一个当前最小值

  1. class MinStack {
  2. public:
  3.     /** initialize your data structure here. */
  4.     int Min=INT_MAX;
  5.     stack<int> st;
  6.     MinStack() {
  8.     }
  9.     void push(int x) {
  10.         st.push(Min);//加入上一个最小值
  11.         if(x<Min) Min=x;//更新最小值
  12.         st.push(x);//加入该数值
  13.     }
  15.     void pop() {
  16.         st.pop();//pop掉该数值
  17.         Min=st.top();//得到去掉该值后的最小值
  18.         st.pop();//将该最小值也pop掉
  19.     }
  21.     int top() {
  22.         return st.top();//返回栈顶即可
  23.     }
  25.     int min() {
  26.         return Min;
  27.     }
  28. };
  30. /**
  31.  * Your MinStack object will be instantiated and called as such:
  32.  * MinStack* obj = new MinStack();
  33.  * obj->push(x);
  34.  * obj->pop();
  35.  * int param_3 = obj->top();
  36.  * int param_4 = obj->min();
  37.  */

2. 我的思路：先存x，再存min

栈中的元素是成对的，表示存入x后，栈中的最小元素是min

class MinStack {
public:
    /** initialize your data structure here. */
    stack<int> st;
    MinStack() {}
    void push(int x) {     
        if (st.empty()) { // 如果栈为空，当前值就是最小值
            st.push(x);
            st.push(x);
        } else {
            int curMin = st.top(); // 当前最小值
            st.push(x);
            if (x < curMin) {
                st.push(x);
            } else {
                st.push(curMin);
            }
        }
    }

    void pop() {
        if (st.empty())
            return;
        st.pop();//pop掉最小值
        st.pop();//将该值也pop掉
    }

    int top() {
        if (st.empty())
            return -1;
        int temp1 = st.top();
        st.pop();
        int temp2 = st.top();
        st.push(temp1);
        return temp2;
    }

    int min() {
        return st.top();
    }
};

/**
 * Your MinStack object will be instantiated and called as such:
 * MinStack* obj = new MinStack();
 * obj->push(x);
 * obj->pop();
 * int param_3 = obj->top();
 * int param_4 = obj->min();
 */

剑指 Offer 31. 栈的压入、弹出序列

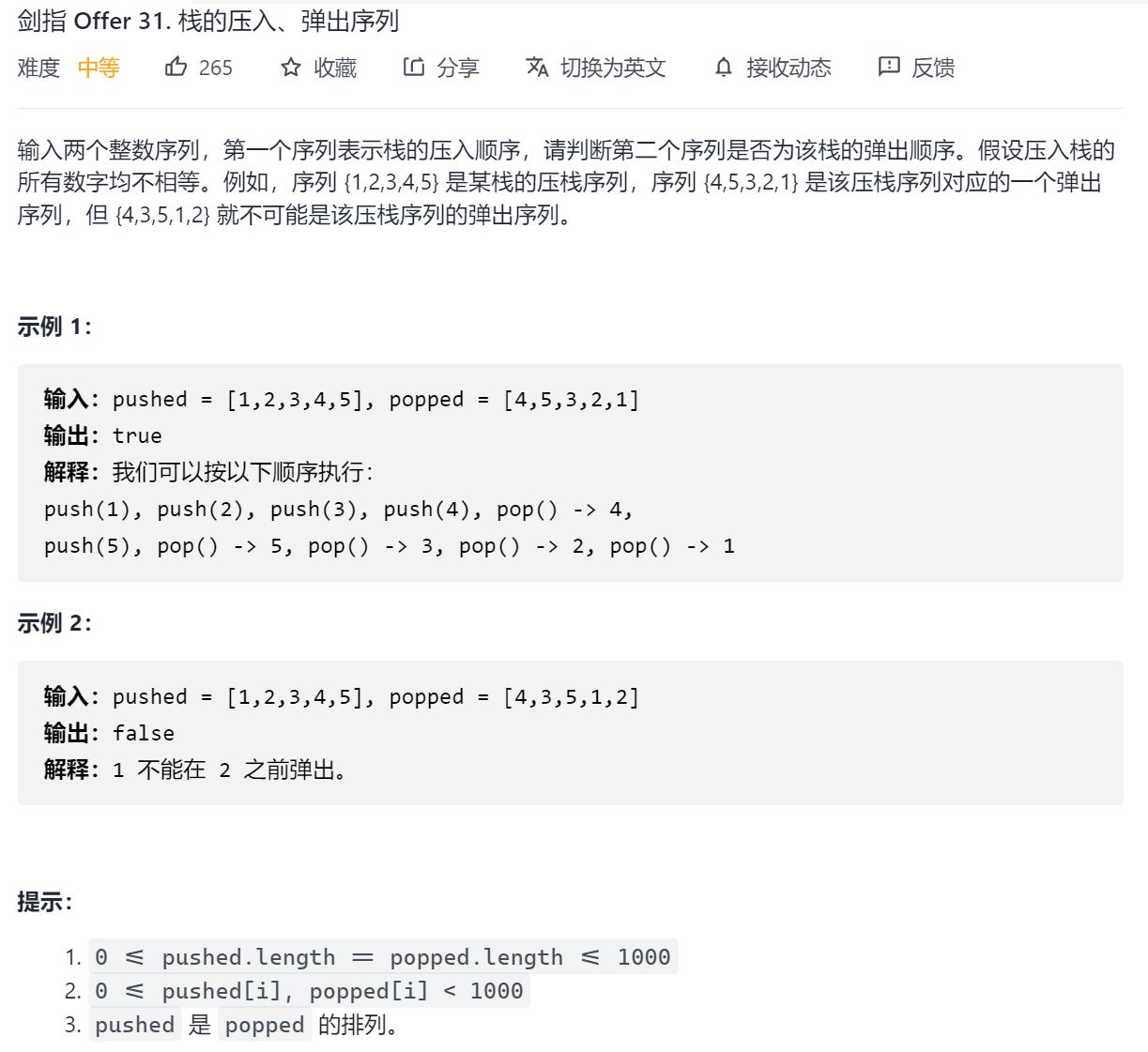
image.png
思路：
用一个辅助栈
如果栈为空或者栈顶元素不等于当前待出栈元素，那么不断将pushed元素压入栈中，如果元素用光还是无法找到待出栈元素，那么返回false
如果栈顶元素和待出栈元素一致，那么将该元素从辅助栈中弹出，访问下一个待出栈元素
所有元素都出栈以后，返回true

class Solution {
public:
    bool validateStackSequences(vector<int>& pushed, vector<int>& popped) {
        stack<int> st;
        int i = 0, j = 0;

        while (i < popped.size()) {
            while (st.empty() || st.top() != popped[i]) {
                if (j == pushed.size())
                    break;
                st.push(pushed[j++]);
            }
            if (st.top() != popped[i])
                break;
            st.pop();
            i++;
        }

        return i == popped.size();
    }
};

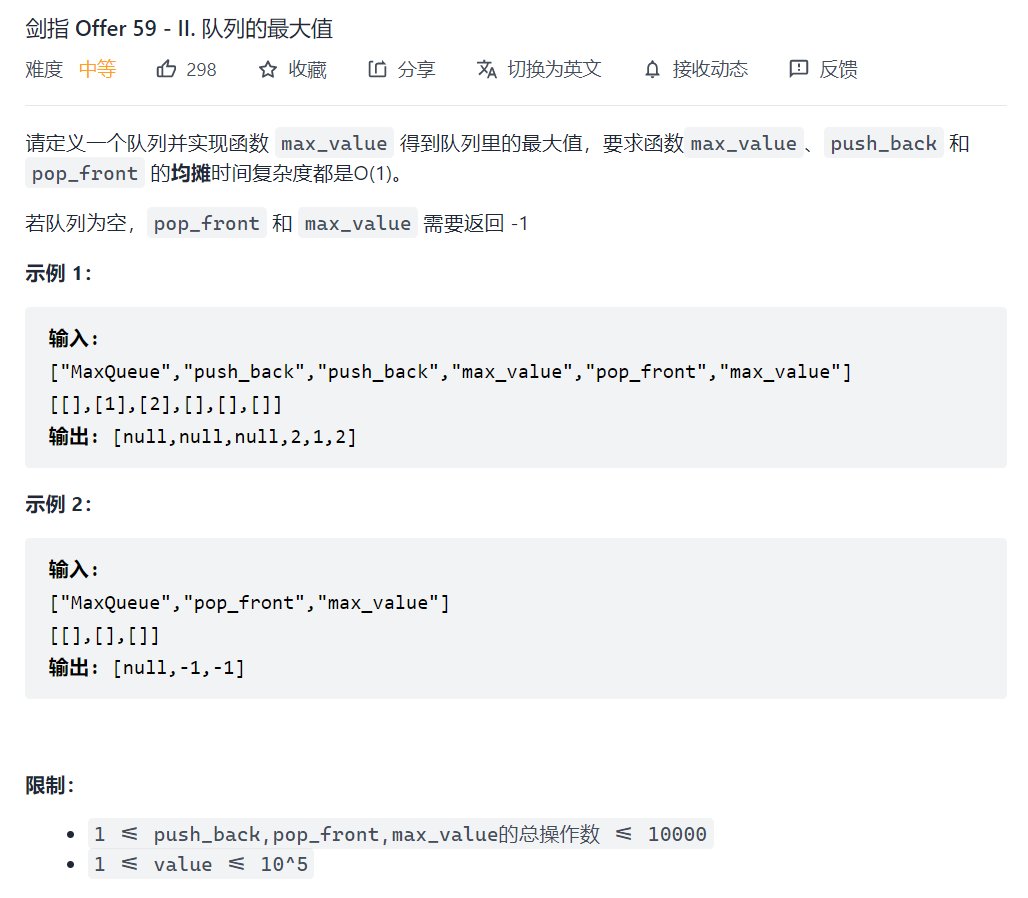
剑指 Offer 59 - I. 滑动窗口的最大值

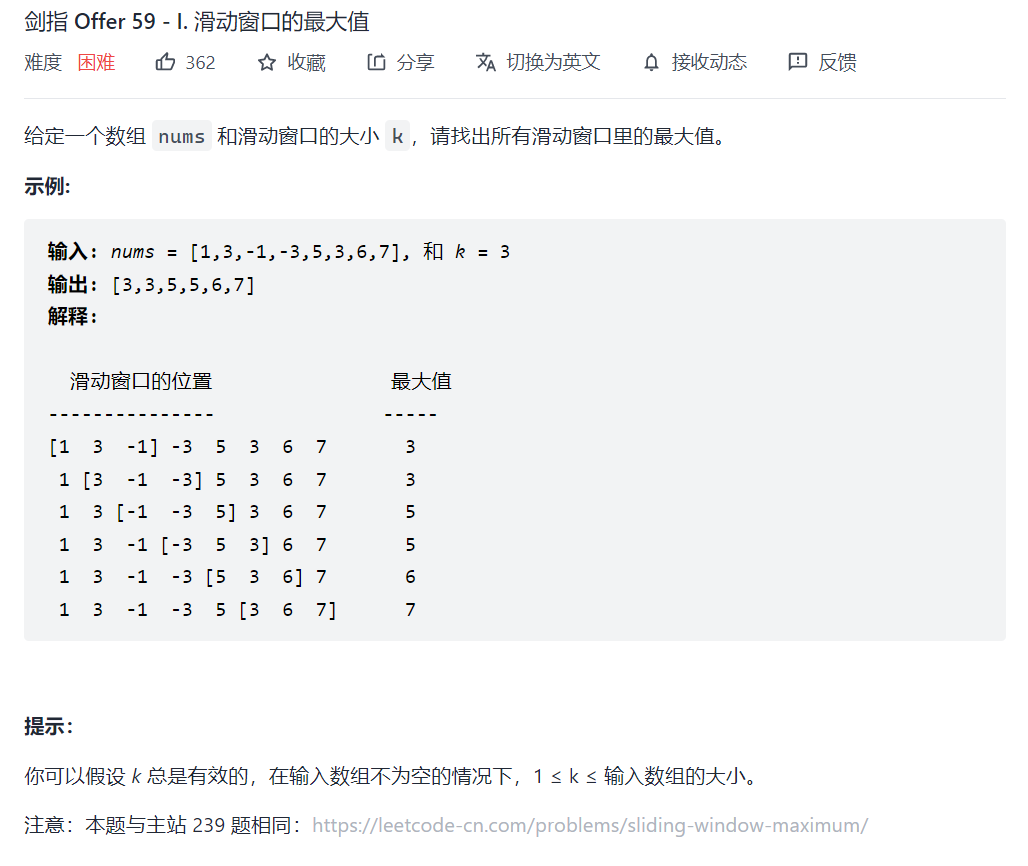
image.png
优先队列

class Solution {
public:
    vector<int> maxSlidingWindow(vector<int>& nums, int k) {
        if (nums.size() == 0) return {};
        priority_queue<pair<int, int>> pq;
        for (int i = 0; i < k; ++i) {
            pq.emplace(nums[i], i);
        }
        vector<int> res;
        res.push_back(pq.top().first);
        for (int i = k; i < nums.size(); ++i) {
            pq.emplace(nums[i], i);
            while (pq.top().second <= i - k) {
                pq.pop();
            }
            res.push_back(pq.top().first);
        }
        return res;
    }
};

单调队列

剑指 Offer 59 - II. 队列的最大值

image.png