1. 冒泡排序
两两交换,第一趟使最大的元素位于最后,第二趟使次大的处于倒数第二位,每一趟处理,都会有一个元素处于最终位置,时间复杂度为O(N^2)
排序后同值元素的相对位置保持不变,具有稳定性(大学考试可能会考,实际上没什么卵用)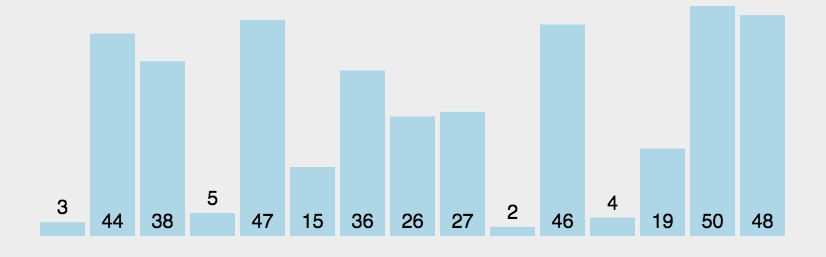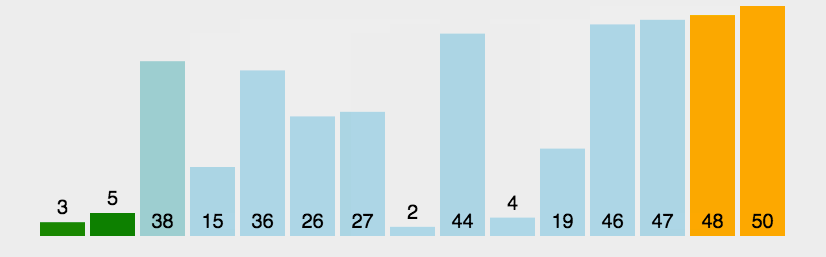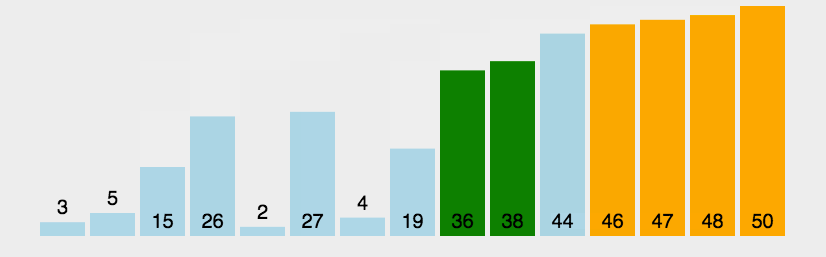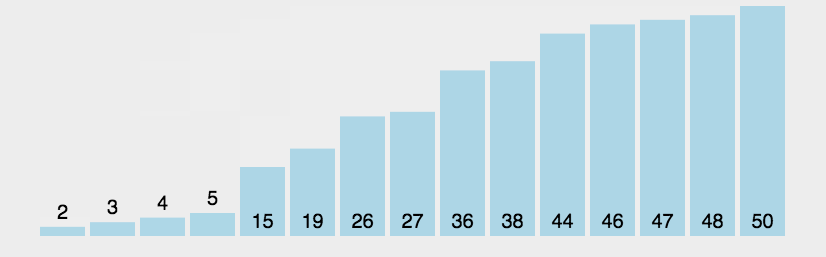
void bubbleSort(vector<int>& v) {for (int i = v.size() - 1; i > 0; i--) {bool flag = true; // 标记是否发生交换,如果没有发生交换,则已经有序,直接结束循环for (int j = 0; j < i; j++) {if (v[j] > v[j + 1]) { // swapint t = v[j];v[j] = v[j + 1];v[j + 1] = t;flag = false;}}if (flag)break;}}
2. 选择排序
第一趟选择所有元素中最小的,和第一位交换;第二趟选择第二位及以后的元素中最小的,和第二位交换;以此类推.(选择最大的和最后一位交换也行,逻辑是一样的)
每一趟处理,都会有一个元素处于最终位置,时间复杂度为O(N^2)
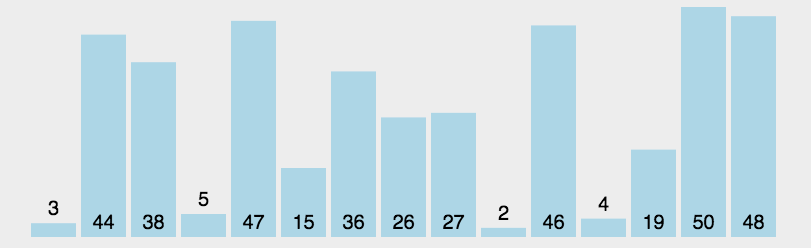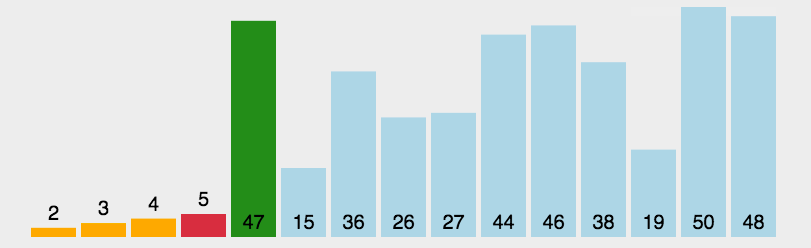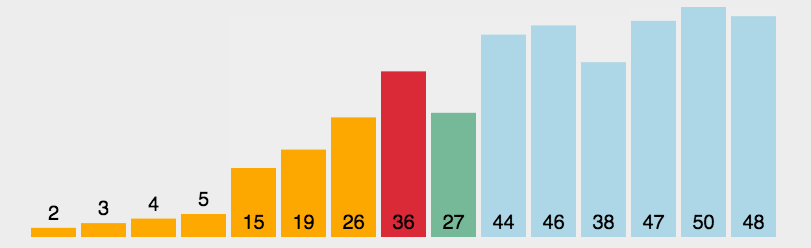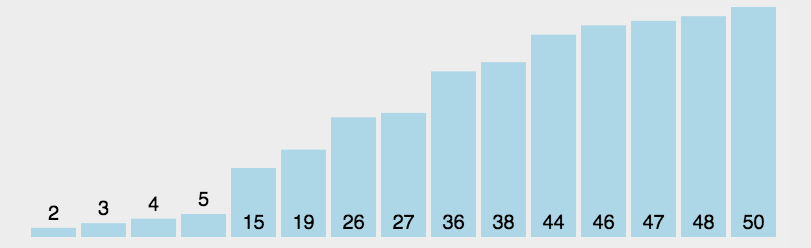
void selectionSrot(vector<int>& v) {for (int i = 0; i < v.size(); i++) {int minIndex = i;for (int j = i + 1; j < v.size(); j++) { // 查找最小元素if (v[j] < v[minIndex]) {minIndex = j;}}// 交换int t = v[i];v[i] = v[minIndex];v[minIndex] = t;}}
3. 插入排序
思路:假设某元素之前的子序列有序,该元素如果大于子序列末端元素则可继续下一个元素;如果该元素小于子序列末端,则往前插入到指定位置
第一趟:第一个元素已经有序
第二趟:第二个元素往前插
第三趟:第三个元素往前两个元素插
……
时间复杂度:O(n²)=1+2+3+…+n-1
空间复杂度:O(1)
原址排序
稳定性:由于是从后往前,后续元素如果存在前面相等的,无法越过,相对位置不会发生变化
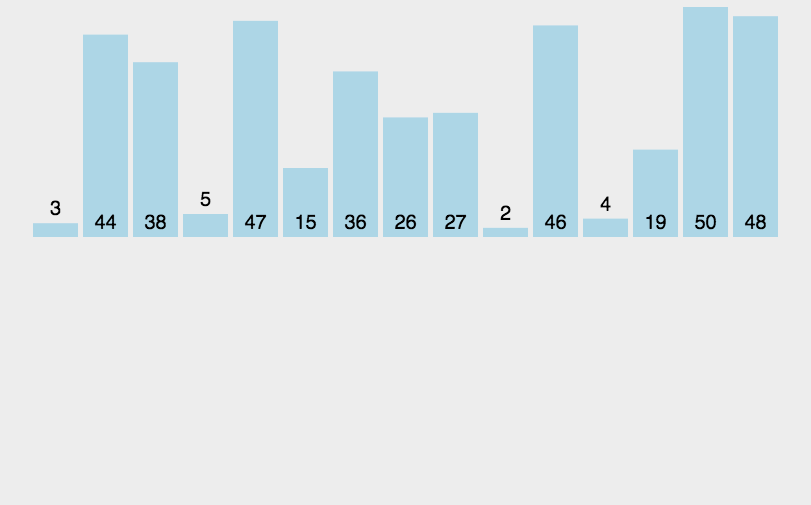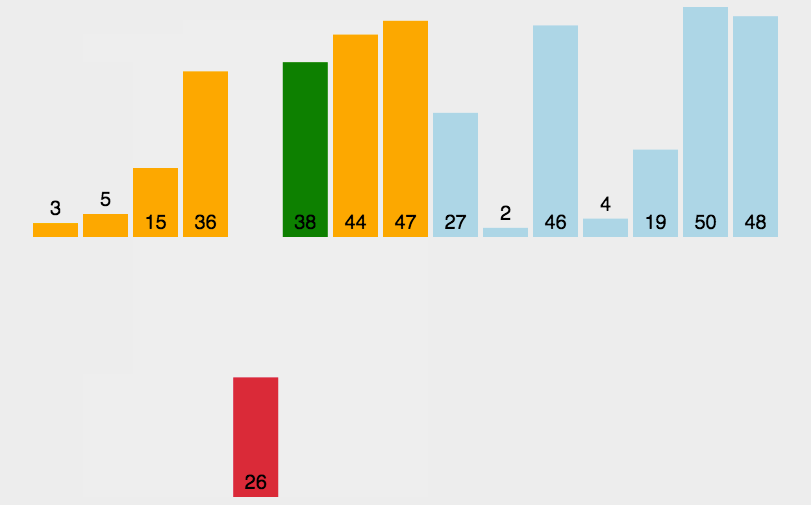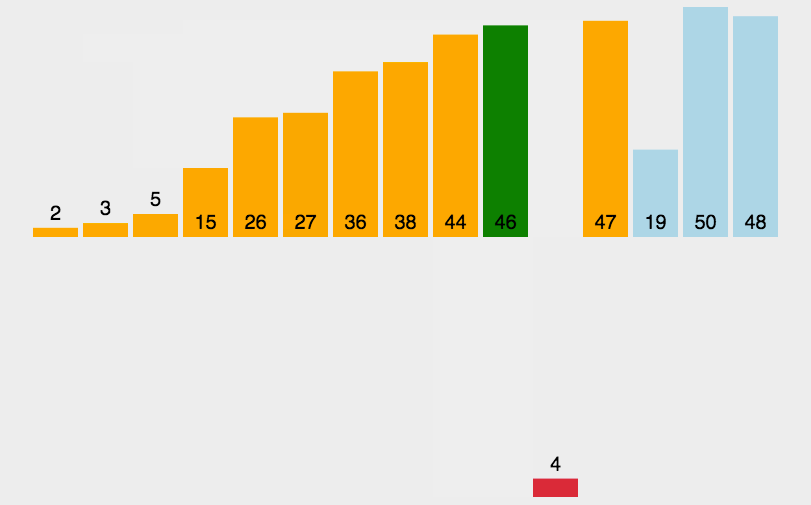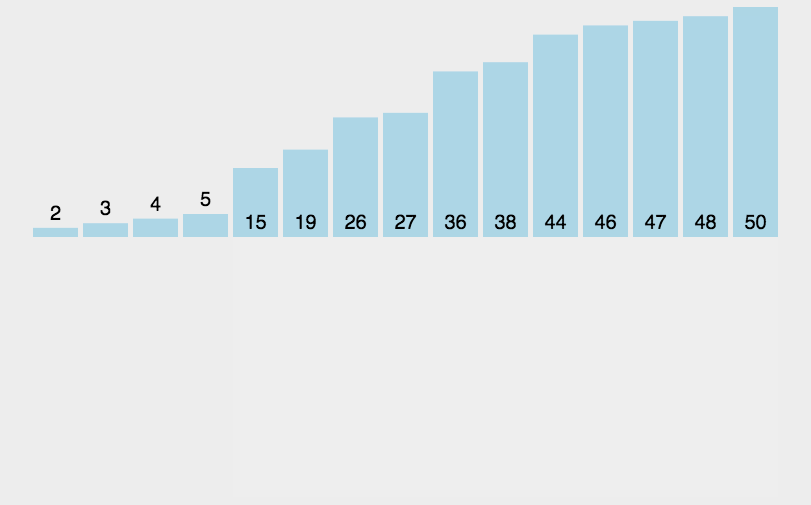
算法第四版上插入的思路,通过交换,值得学习
void insertSort(vector<int>& v) {for (int i = 0; i < v.size(); i++) {for (int j = i; j > 0 && v[j - 1] > v[j]; j--) {// 通过交换将元素插入合适的位置int t = v[j];v[j] = v[j - 1];v[j - 1] = t;}}}
4. 希尔排序
希尔排序是插入排序的一种。
也称缩小增量排序,是直接插入排序算法的一种更高效的改进版本。希尔排序是非稳定排序算法
思路:如序列 9 8 7 6 5 4 3 2 1
确定一个增量序列,如 4(length/2) 2 1 ,从大到小使用增量
使用第一个增量,将序列划分为若干个子序列,下标组合为0-4-8,1-5,2-6,3-7
依次对子序列使用直接插入排序法;
使用第二个增量,将序列划分为若干个子序列(0-2-4-6-8),(1-3-5-7)
依次对子序列使用直接插入排序法:
使用第三个增量1,这时子序列就是元序列(0-1-2-3-4-5-6-7-8),使用直接插入法
完成排序。
时间复杂度:不太确定在O(nlogn)~O(n²)之间
空间复杂度:O(1)
原址排序
稳定性:由于相同的元素可能会被划分至不同子序列单独排序,因此稳定性是无法保证的——不稳定 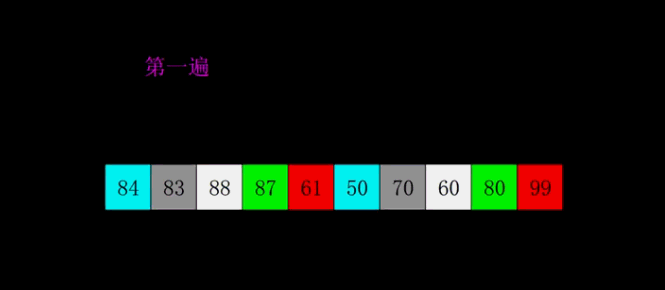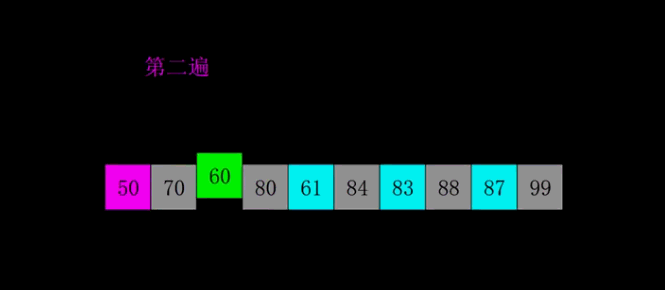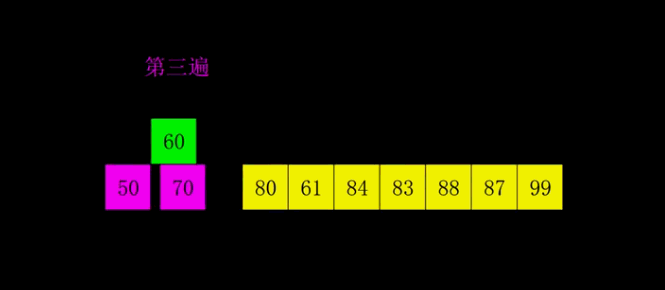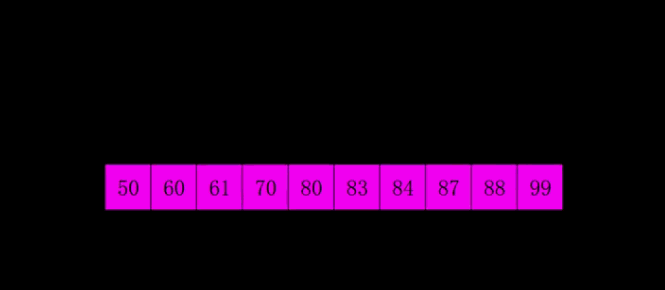
void shellSort(vector<int>& v) {int len = v.size();int interval = len / 2; //增量,一般初始设为长度的一半// while (h < len / 3)// h = 3 * h + 1;while (interval >= 1) {// 第一个循环,改变间隔的大小for (int i = interval; i < len; i++) {// i向前推进的同时,用j来对每个子序列进行插入排序,很秒for (int j = i; j >= interval && v[j] < v[j - interval]; j -= interval) {int t = v[j];v[j] = v[j - interval];v[j - interval] = t;}}interval /= 2;}}
5. 快速排序
快速排序的基本思想:通过一趟排序将待排记录分隔成独立的两部分,其中一部分记录的关键字均比另一部分的关键字小,则可分别对这两部分记录继续进行排序,以达到整个序列有序。
快速排序使用分治法来把一个串(list)分为两个子串(sub-lists)。具体算法描述如下:
- 从数列中挑出一个元素,称为 “基准”(pivot);
- 重新排序数列,所有元素比基准值小的摆放在基准前面,所有元素比基准值大的摆在基准的后面(相同的数可以到任一边)。在这个分区退出之后,该基准就处于数列的中间位置。这个称为分区(partition)操作;
- 递归地(recursive)把小于基准值元素的子数列和大于基准值元素的子数列排序。
pivot的选择:
- 最左边元素
- 最右边元素
- 中间元素
选择两端的元素为pivot如果数组本身有序的话,可能会TLE
快排的一般写法,这段代码没有把分区单独封装
void quickSort(vector<int>& v, int l, int r) {// 子数组长度为 1 时终止递归if (l >= r) return;// 哨兵划分操作(以 arr[l] 作为基准数)int i = l, j = r;while (i < j) {while (i < j && arr[j] >= arr[l]) j--; // 找到第一个小于枢轴的数while (i < j && arr[i] <= arr[l]) i++; // 找到第一个大于枢轴的数swap(arr[i], arr[j]); // 交换}swap(arr[i], arr[l]);// 递归左(右)子数组执行哨兵划分quickSort(arr, l, i - 1);quickSort(arr, i + 1, r);}
划分的时候有单向扫描分区法,双指针双向扫描分区法,还有三点中值法使得选择的枢轴尽量是中值
快速排序初始数组越乱,效率越高,平均效率为O(nlogN)
👌模板:
#include <iostream>#include <cstring>#include <algorithm>using namespace std;const int N = 100010;int x[N];void quickSort(int x[], int l, int r) {if (l >= r) return; // 没有元素或者只有一个int i = l - 1, j = r + 1, pivot = x[l + r >> 1]; // 去中间元素为枢轴 样例有有序大数组,选择两端会TLEwhile (i < j) {while (x[++i] < pivot);while (x[--j] > pivot);if (i < j) swap(x[i], x[j]);}quickSort(x, l, j);quickSort(x, j + 1, r);}int main() {int n;cin >> n;for (int i = 0; i < n; ++i) cin >> x[i];quickSort(x, 0, n - 1);for (int i = 0; i < n; ++i) cout << x[i] << " ";return 0;}
快速选择算法查找第k个数
快速排序的步骤:
- 选择pivot
- 划分为左右两个区间
- 递归处理左右两个区间
如果pivot前面有left个元素,假如left > k,说明排序后第k个元素位于枢轴左边,递归处理左区间,反之递归处理右区间。
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 100010;
int x[N];
int quickSelect(int x[], int l, int r, int k) {
if (l >= r) return x[l];
int i = l - 1, j = r + 1, pivot = x[l + r >> 1];
while (i < j) {
while (x[++i] < pivot);
while (x[--j] > pivot);
if (i < j) swap(x[i], x[j]);
}
int len = j - l + 1; // pivot前面的元素个数
if (len >= k) return quickSelect(x, l, j, k); // 处理左区间
else return quickSelect(x, j + 1, r, k - len); // 处理有区间,找右区间的第k - len个元素
}
int main() {
int n, k;
cin >> n >> k;
for (int i = 0; i < n; ++i) cin >> x[i];
cout << quickSelect(x, 0, n - 1, k) << endl;
return 0;
}
6. 归并排序
归并排序使用的是分治的思想,先让部分有序,然后进行归并,最终使整体有序
归并排序需要一个辅助空间,空间复杂度为O(N),时间复杂度为 O(NlogN)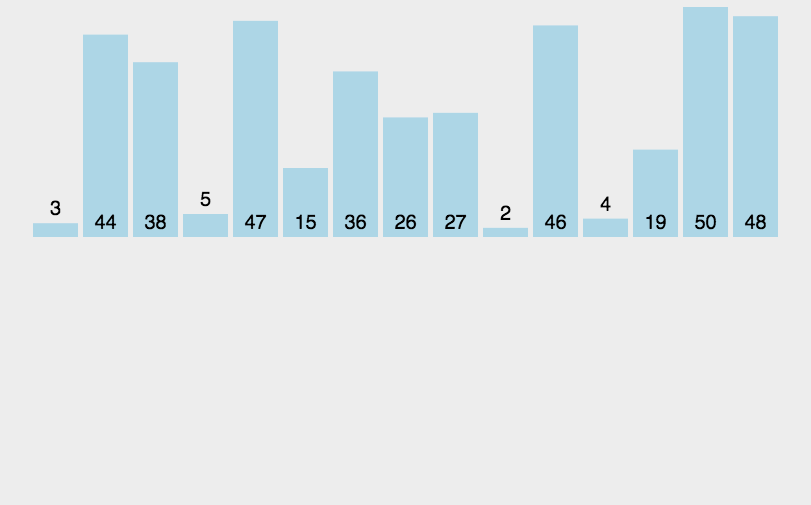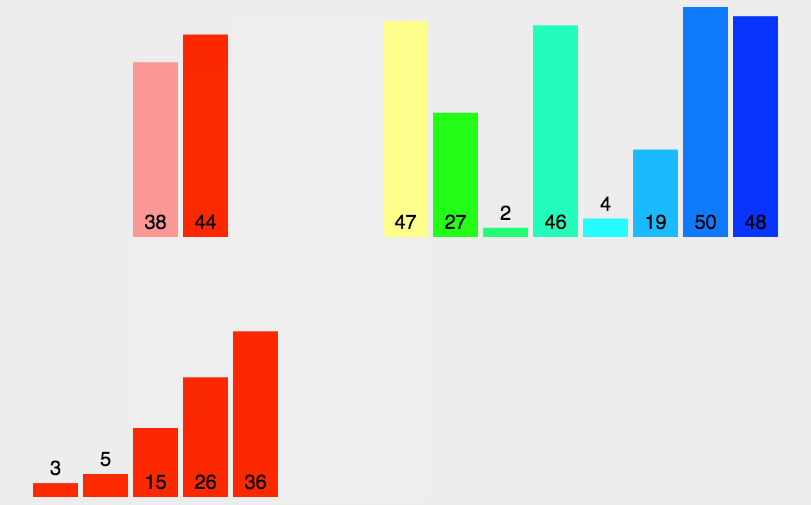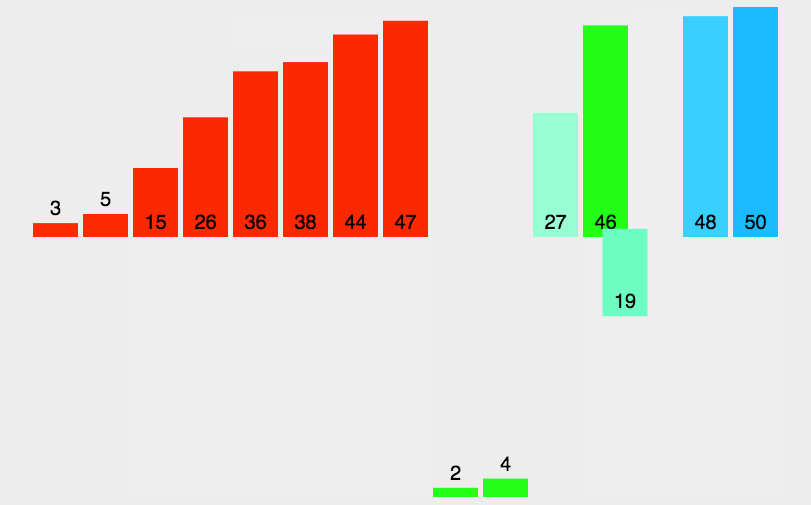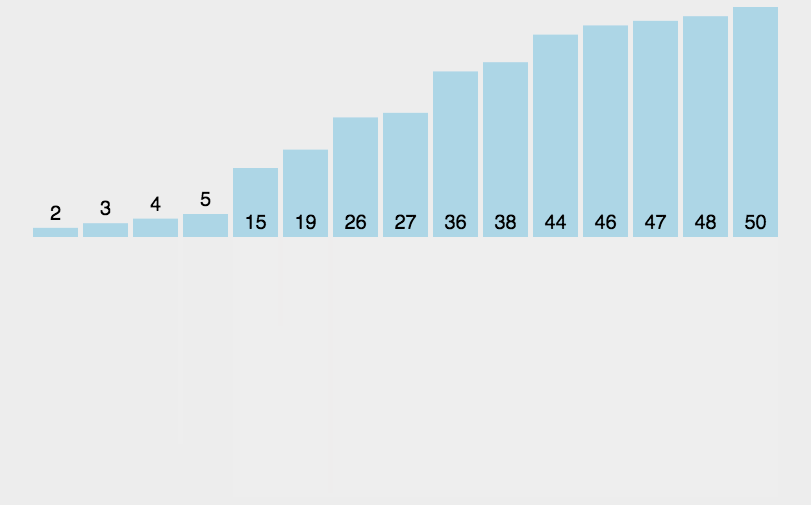
步骤:
- 确定分界点(中间点),将数组分为左右两部分
- 递归排序左右两部分
- merge
版本1:
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 100010;
int a[N], tmp[N];
void merge_sort(int a[], int l, int r) {
if (l >= r) return;
int mid = (l + r) >> 1;
merge_sort(a, l, mid);
merge_sort(a, mid + 1, r);
int i = l, j = mid + 1, k = l;
while (i <= mid && j <= r) {
if (a[i] <= a[j]) tmp[k++] = a[i++];
else tmp[k++] = a[j++];
}
while (i <= mid) tmp[k++] = a[i++];
while (j <= r) tmp[k++] = a[j++];
for (int i = l; i <= r; ++i) a[i] = tmp[i];
}
int main() {
int n;
cin >> n;
for (int i = 0; i < n; ++i) scanf("%d", &a[i]);
merge_sort(a, 0, n - 1);
for (int i = 0; i < n; ++i) printf("%d ", a[i]);
return 0;
}
版本2:
void merge(vector<int>& v, int left, int mid, int right) { // 左闭右闭
// 相当于将两个数组合并成一个有序数组
int n = right - left + 1;
vector<int> helper(v.begin(), v.end());
int cur = left;
int p1 = left, p2 = mid + 1;
while (p1 <= mid && p2 <= right) {
if (helper[p1] < helper[p2]) {
v[cur++] = helper[p1++];
} else {
v[cur++] = helper[p2++];
}
}
while (p1 <= mid) { // 右边没处理完的话,不用处理
v[cur++] = helper[p1++];
}
}
void mergeSort(vector<int>& v, int left, int right) { // 左闭右闭
if (left < right) {
int mid = left + ((right - left) >> 1);
mergeSort(v, left, mid); // 处理左半部分
mergeSort(v, mid + 1, right); // 处理右半部分
merge(v, left, mid, right); // 归并
}
}
归并排序的应用,求逆序对的个数
归并的过程中,如果左半边的数组出现了大于右半边数组中对应位置的元素,那么左半边数组中剩余的所有元素都比右半边这个元素大,那么逆序对的个数加 mid - i + 1,即左边剩余元素的个数
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
typedef long long ll;
const int N = 100010;
int a[N], tmp[N];
ll mergeSort(int a[], int l, int r) {
if (l >= r) return 0;
int mid = (l + r) >> 1;
long long res = mergeSort(a, l, mid) + mergeSort(a, mid + 1, r);
int i = l, j = mid + 1, k = l;
while (i <= mid && j <= r) {
if (a[i] <= a[j]) tmp[k++] = a[i++];
else {
tmp[k++] = a[j++];
res += mid - i + 1;
}
}
while (i <= mid) tmp[k++] = a[i++];
while (j <= r) tmp[k++] = a[j++];
for (int i = l; i <= r; i++) a[i] = tmp[i];
return res;
}
int main() {
int n;
cin >> n;
for (int i = 0; i < n; i++) scanf("%d", &a[i]);
cout << mergeSort(a, 0, n - 1) << endl;
return 0;
}
还有一个常考的题,求小数和
#include<iostream>
using namespace std;
const int N = 100010;
int n;
int a[N], tmp[N];
long long res;
void merge_sort(int a[], int l, int r) {
if (l >= r) return;
int mid = (l + r) >> 1;
merge_sort(a, l, mid);
merge_sort(a, mid + 1, r);
// merge
int k = l, i = l, j = mid + 1;
while (i <= mid && j <= r) {
if (a[i] <= a[j]) { // 找到a[j]左边比它小的数
res += a[i] * (r - j + 1); // a[i]比a[j]右边的数也小
tmp[k++] = a[i++];
} else {
tmp[k++] = a[j++];
}
}
while (i <= mid) tmp[k++] = a[i++];
while (j <= r) tmp[k++] = a[j++];
for (int i = l; i <= r; i++) a[i] = tmp[i];
}
int main() {
cin >> n;
for (int i = 0; i < n; i++) cin >> a[i];
merge_sort(a, 0 , n - 1);
cout << res << endl;
return 0;
}
7. 计数排序
计数排序:创建一个辅助数组,以数据元素为索引,统计出现的次数,然后按照辅助数组下标和计数进行输出,得到一个有序(升)数列
优点:快
缺点:数组数据范围较大时,浪费空间
适用范围:数据范围较小,额外空间能接受
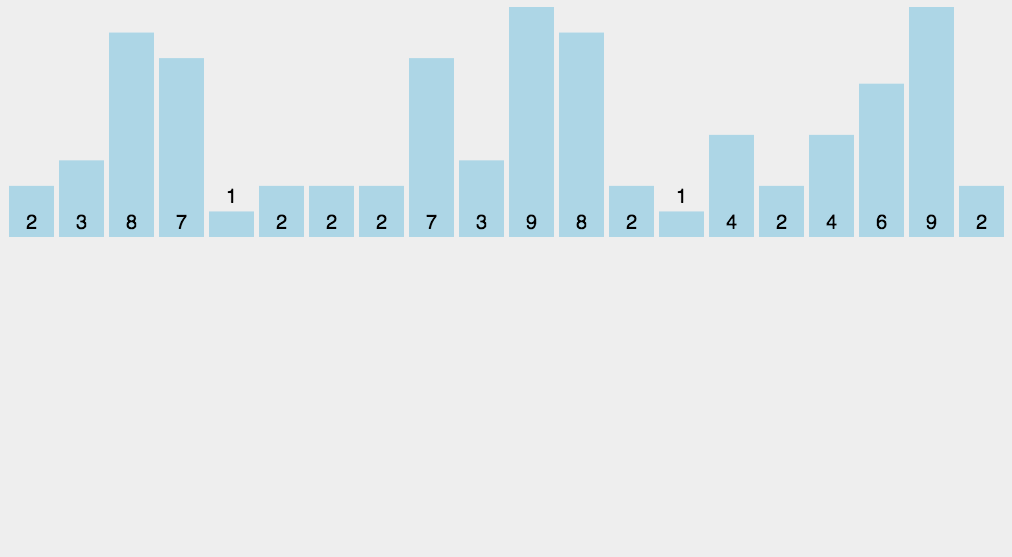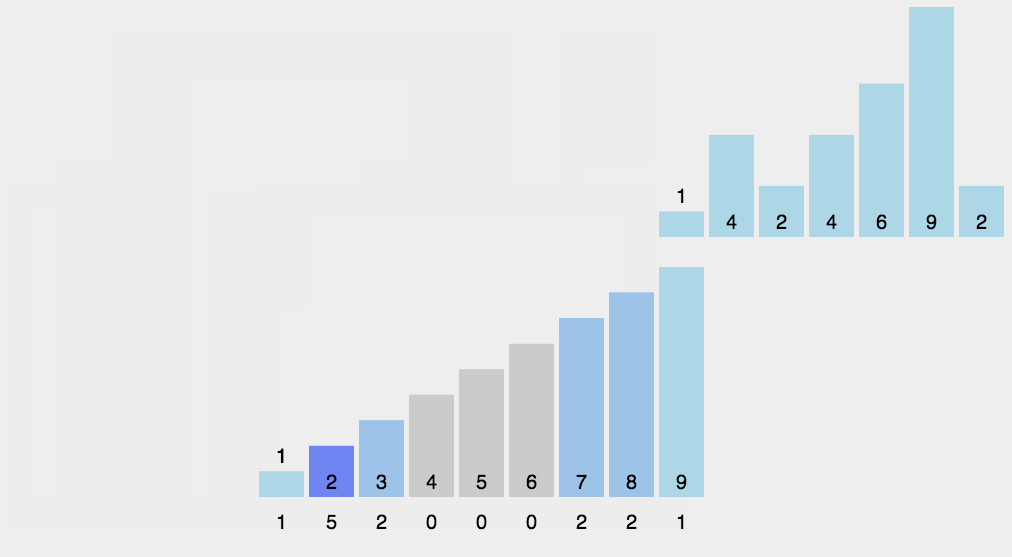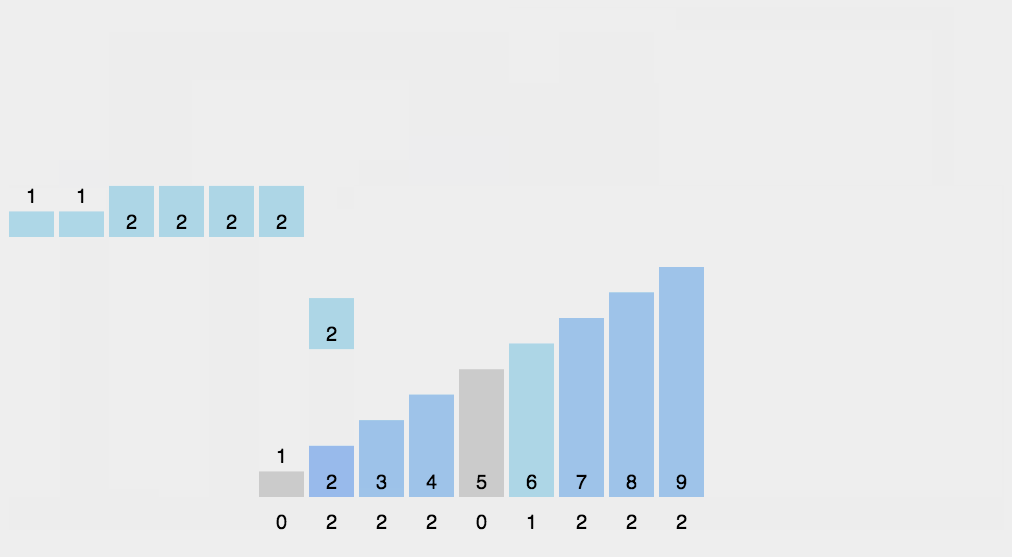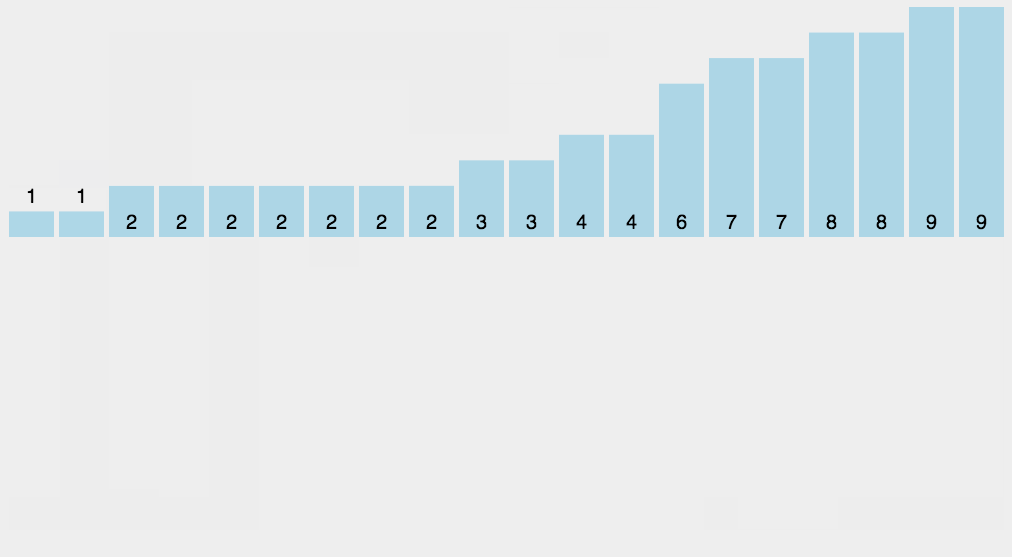
void countSort(vector<int>& v) {
int maxNum = INT32_MIN;
for (auto num : v) {
maxNum = max(maxNum, num);
}
vector<int> helper(maxNum + 1, 0); // 辅助数组用于计数
// 统计出现的次数
for (auto num : v) {
helper[num]++;
}
// 根据辅助数组来进行排序
int cur = 0;
for (int i = 0; i < helper.size(); i++) {
while (helper[i]) {
v[cur++] = i;
helper[i]--;
}
}
}
计数排序是一个稳定?的排序算法。当输入的元素是 n 个 0到 k 之间的整数时,时间复杂度是O(n+k),空间复杂度也是O(n+k),其排序速度快于任何比较排序算法。当k不是很大并且序列比较集中时,计数排序是一个很有效的排序算法。
8. 桶排序
桶排序是计数排序的升级版。计数排序可以看成每个桶只存储相同元素,而桶排序每个桶存储一定范围的元素,通过映射函数,将待排序数组中的元素映射到各个对应的桶中,对每个桶中的元素进行排序,最后将非空桶中的元素逐个放入原序列中。
桶排序需要尽量保证元素分散均匀,否则当所有数据集中在同一个桶中时,桶排序失效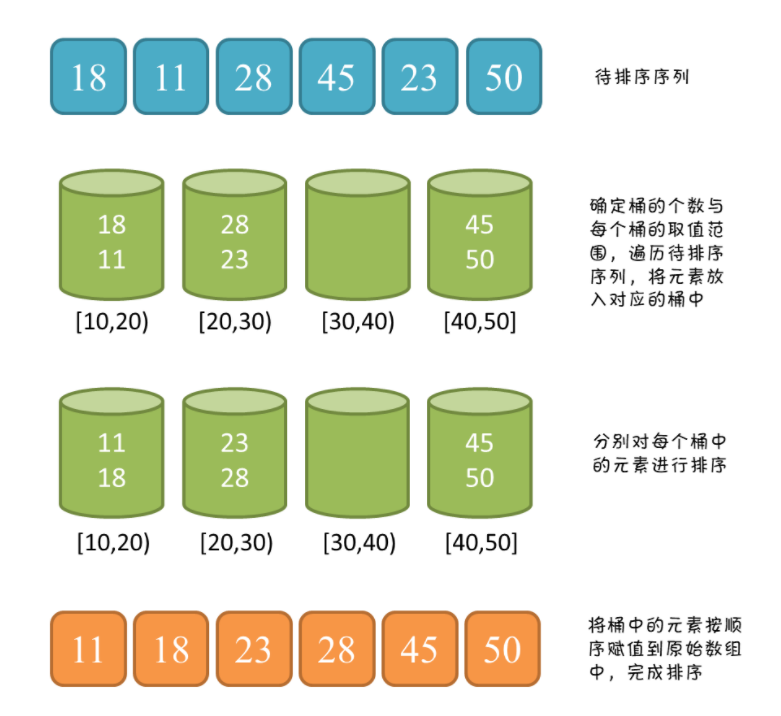
桶排序需要用链表(动态数组也行)来存储每个桶中的元素
void bucketSort(vector<int>& v) {
if (v.size() == 0)
return;
int maxNum = v[0], minNum = v[0];
for (auto num : v) {
maxNum = max(maxNum, num);
minNum = min(minNum, num);
}
// 计算桶的数量
int bucketNum = (maxNum - minNum) / v.size() + 1; //这个自己定义也行
vector<vector<int>> buckets(bucketNum);
// 元素入桶子
for (auto num: v) {
int n = (num - minNum) / v.size(); // 计算映射到哪个桶
buckets[n].push_back(num);
// 寻找正确的插入位置
for (int i = buckets[n].size() - 1; i > 0 && buckets[n][i] < buckets[n][i - 1]; i++) {
int temp = buckets[n][i];
buckets[n][i] = buckets[n][i - 1];
buckets[n][i - 1] = temp;
}
}
int cur = 0;
for (auto bucket : buckets) {
for (int i = 0; i < bucket.size(); i++) {
v[cur++] = bucket[i];
}
}
}
9. 基数排序
基数排序是按照低位先排序,然后收集;再按照高位排序,然后再收集;依次类推,直到最高位。有时候有些属性是有优先级顺序的,先按低优先级排序,再按高优先级排序。最后的次序就是高优先级高的在前,高优先级相同的低优先级高的在前。
算法描述:
- 取得数组中的最大数,并取得位数;
- arr为原始数组,从最低位开始取每个位组成radix数组;
- 对radix进行计数排序(利用计数排序适用于小范围数的特点);

void radixSort(vector<int>& v) {
if (v.size() == 0)
return;
// 寻找最大的元素,计算位数
int maxNum = v[0];
for (auto num : v) {
maxNum = max(maxNum, num);
}
int pos = 0;
while (maxNum) {
pos++;
maxNum /= 10;
}
const int BUCKETS = 10;
vector<vector<int>> buckets(BUCKETS);
//外层循环是根据数字的位数确定的
for (int i = 0; i < pos; i++) {
// i = 0, 表示个位数; i = 1, 表示十位数; 以此类推
int denominator = static_cast<int>(pow(10, i)); // 取某一位数的时候需要用的分母
for (int & tmp : v) // 按数字放入桶中
buckets[(tmp / denominator) % 10].push_back(tmp);
int index = 0;
// 从桶中取出来,放入原来的source序列中,以备下次遍历时使用
for (auto & theBucket : buckets) {
for (int & k : theBucket)
v[index++] = k;
theBucket.clear();//一定要清空桶中数据
}
}
}
基数排序基于分别排序,分别收集,所以是稳定的。但基数排序的性能比桶排序要略差,每一次关键字的桶分配都需要O(n)的时间复杂度,而且分配之后得到新的关键字序列又需要O(n)的时间复杂度。假如待排数据可以分为d个关键字,则基数排序的时间复杂度将是O(d*2n) ,当然d要远远小于n,因此基本上还是线性级别的。
基数排序的空间复杂度为O(n+k),其中k为桶的数量。一般来说n>>k,因此额外空间需要大概n个左右。
10. 堆排序
堆排序(Heapsort)是指利用堆这种数据结构所设计的一种排序算法。堆积是一个近似完全二叉树的结构,并同时满足堆积的性质:即子结点的键值或索引总是小于(或者大于)它的父节点。
算法描述
- 将初始待排序关键字序列(R1,R2….Rn)构建成大顶堆,此堆为初始的无序区;
- 将堆顶元素R[1]与最后一个元素R[n]交换,此时得到新的无序区(R1,R2,……Rn-1)和新的有序区(Rn),且满足R[1,2…n-1]<=R[n];
- 由于交换后新的堆顶R[1]可能违反堆的性质,因此需要对当前无序区(R1,R2,……Rn-1)调整为新堆,然后再次将R[1]与无序区最后一个元素交换,得到新的无序区(R1,R2….Rn-2)和新的有序区(Rn-1,Rn)。不断重复此过程直到有序区的元素个数为n-1,则整个排序过程完成。

堆排序代码实现的流程:
建堆→将堆顶元素与数组未处理部分的最后一个元素交换→调整→将堆顶元素与数组未处理部分的最后一个元素交换→调整→…
如果要进行升序排序,可以建立小顶堆,每次输出堆顶(最大元素),将栈顶元素放在数组末尾,最后形成一个单调不减的数组
处理的过程中利用完全二叉树的性质,可以方便计算左右节点、父节点的下标
// 建立大顶堆
void makeHeap(vector<int>& v) {
int n = v.size();
for (int i = n / 2 - 1; i >= 0; i--) {
fixDown(v, i, n);
}
}
// 调整
void fixDown(vector<int>& v, int k, int n) {
int left = 2 * k + 1;
int right = 2 * k + 2;
if (left >= n) { // 如果左孩子越界,当前节点是叶子结点,不用调整
return;
}
int maxChild;
if (right >= n) { // 右孩子越界
maxChild = left;
} else {
maxChild = v[left] > v[right] ? left : right; // max指向较大的元素
}
if (v[k] >= v[maxChild])
return; // 父节点比孩子大,不用交换
// 父节点与最大的孩子交换
int temp = v[k];
v[k] = v[maxChild];
v[maxChild] = temp;
// 递归调整
fixDown(v, maxChild, n);
}
void heapSort(vector<int>& v) {
makeHeap(v); // 建堆
for (int i = v.size() - 1; i >= 0; i--) {
int temp = v[0];
v[0] = v[i];
v[i] = temp;
fixDown(v, 0, i);
}
}
时间复杂度: 堆化:一半的元素修复,修复是单分支的,所以整体堆化为 n*lgn / 2
排序:n个元素都要取出,因此调整n次,每次调整修复同上是lgn的,整体为O(nlgn)
空间复杂度:不需要开辟辅助空间
原址排序

