144. 二叉树的前序遍历

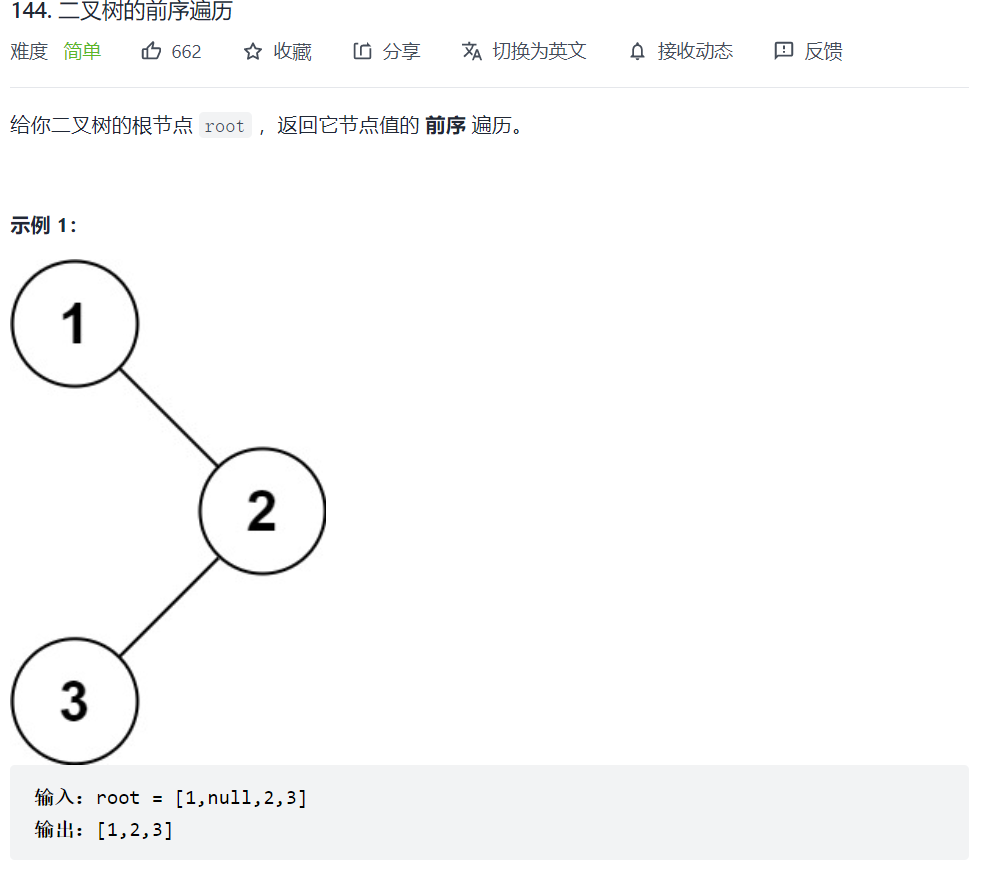
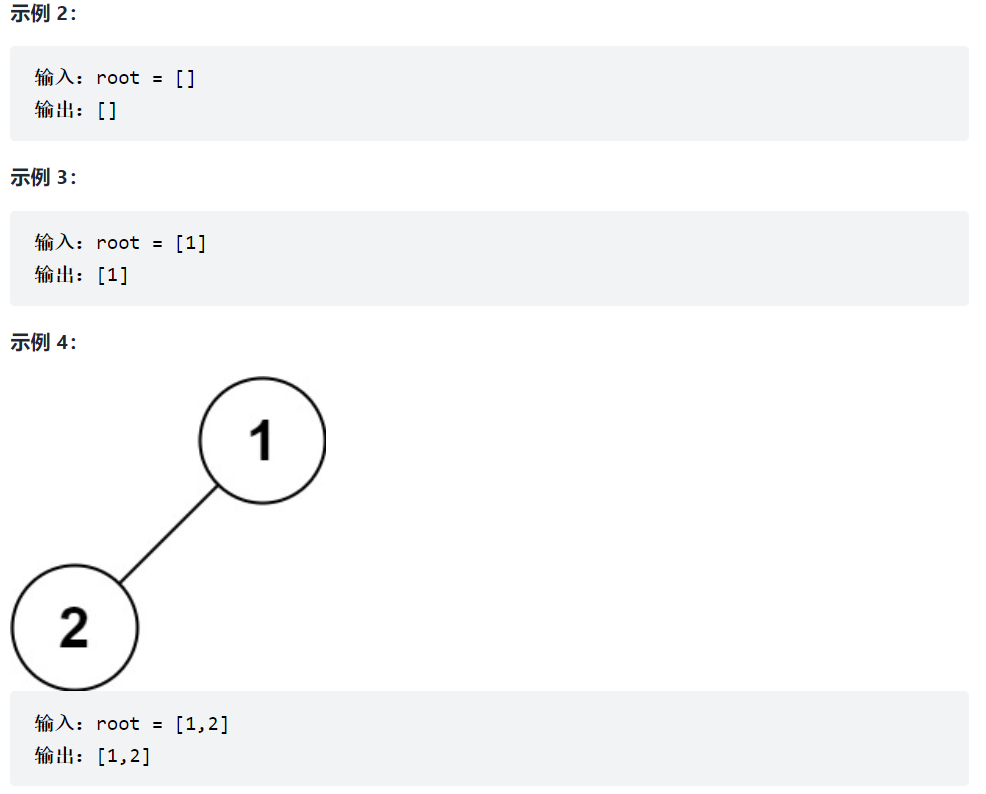
先序遍历：先根再左再右

二叉树的定义：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */

递归遍历

C++代码：

public:
    vector<int> preorderTraversal(TreeNode* root) {
        vector<int> res;
        traversal(root, res);
        return res;
    }
    void traversal(TreeNode * cur, vector<int> &v) {
        // 递归出口
        if (cur == nullptr)
            return;
        // 先访问根结点，然后再递归遍历左右子树
        v.push_back(cur->val);
        traversal(cur->left, v);
        traversal(cur->right, v);
    }
};

迭代遍历

class Solution {
public:
    vector<int> preorderTraversal(TreeNode* root) {
        vector<int> res;
        stack<TreeNode*> stk;
        if (root == nullptr) return res;
        stk.push(root);
        while (!stk.empty()) {
            // 访问根结点
            TreeNode* cur = stk.top();
            stk.pop();
            res.push_back(cur->val);
            // 右孩子先入栈，先入的后被访问
            if (cur->right)
                stk.push(cur->right);
            if (cur->left)
            stk.push(cur->left);
        }
        return res;
    }
};

145. 二叉树的后序遍历

先序遍历：先左再右最后访问根结点

递归遍历

class Solution {
public:
    vector<int> postorderTraversal(TreeNode* root) {
        vector<int> res;
        traversal(root, res);
        return res;
    }

    void traversal(TreeNode *cur, vector<int> &v) {
        // 递归出口
        if (cur == nullptr)
            return;

        // 先遍历左右子树,最后访问根结点
        traversal(cur->left, v);
        traversal(cur->right, v);
        v.push_back(cur->val);
    }
};

迭代遍历

后序遍历的关键在于，当访问完节点的左子树后，如果右子树为空或者已经访问过，才能访问这个节点

class Solution {
public:
    vector<int> postorderTraversal(TreeNode* root) {
        if (root == nullptr) return {};
        stack<TreeNode*> st;
        vector<int> res;
        TreeNode* cur = root;
        TreeNode* pre = nullptr; // 用于判断右子树是否处理
        while (cur != nullptr || !st.empty()) {
            while (cur != nullptr) { // 处理左子树
                st.push(cur);
                cur = cur->left;
            }
            // 左子树处理完毕，处理根和右子树
            cur = st.top();
            st.pop();
            if (cur->right == nullptr || pre == cur->right) { // 如果没有右孩子或者右孩子已经访问过，访问根
                res.push_back(cur->val);
                pre = cur; // 记住此次访问的节点
                cur = nullptr; // 表示这根子树处理完毕，接下来从栈中取节点处理
            } else {
                st.push(cur); // 右子树未处理，先处理右子树，因此将根节点再次放回栈中
                cur = cur->right;
            }
        }
        return res;
    }
};

当然，先序遍历是中左右，后续遍历是左右中，那么我们只需要调整一下先序遍历的代码顺序，就变成中右左的遍历顺序，然后在反转result数组，输出的结果顺序就是左右中了，如下图：
二叉树的遍历 - 图5

class Solution {
public:
    vector<int> postorderTraversal(TreeNode* root) {
        stack<TreeNode*> st;
        vector<int> result;
        if (root == NULL) return result;
        st.push(root);
        while (!st.empty()) {
            TreeNode* node = st.top();
            st.pop();
            result.push_back(node->val);
            if (node->left) st.push(node->left); // 相对于前序遍历，这更改一下入栈顺序 （空节点不入栈）
            if (node->right) st.push(node->right); // 空节点不入栈
        }
        reverse(result.begin(), result.end()); // 将结果反转之后就是左右中的顺序了
        return result;
    }
};

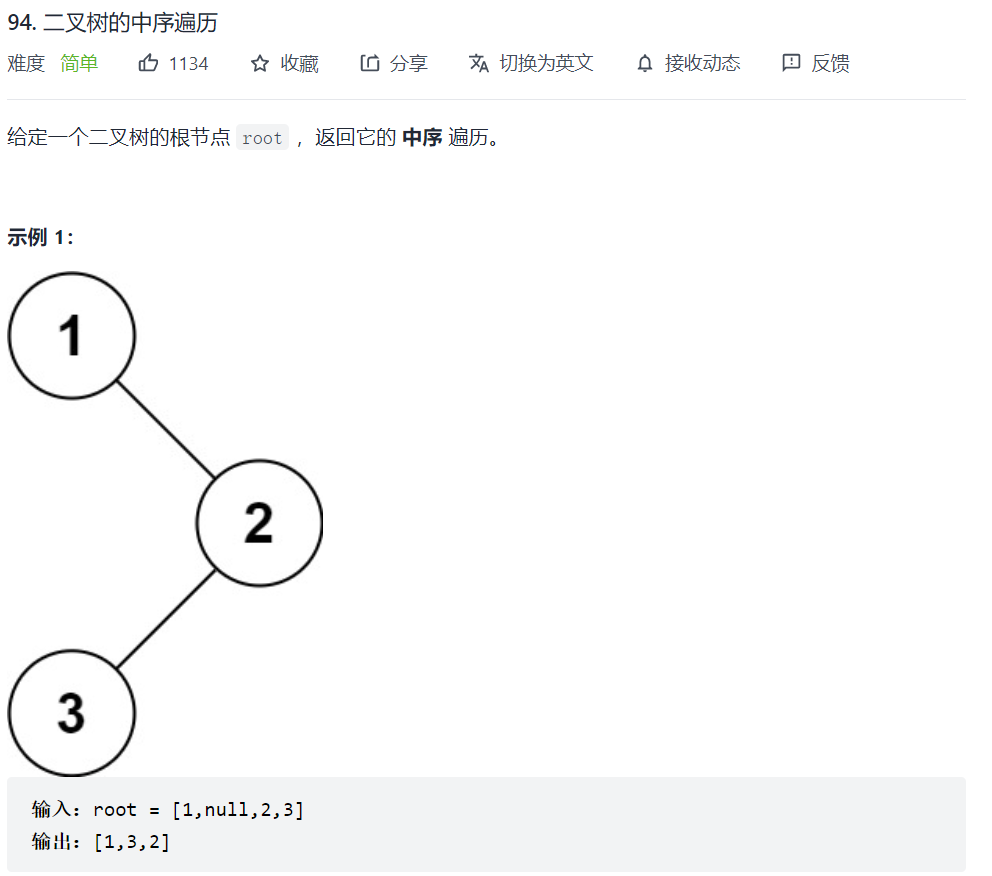
94. 二叉树的中序遍历

先序遍历：先左再根最后右

递归遍历

class Solution {
public:
    vector<int> inorderTraversal(TreeNode* root) {
        vector<int> res;
        traversal(root, res);
        return res;
    }

    void traversal(TreeNode *cur, vector<int> &v) {
        // 递归出口
        if (cur == nullptr)
            return;

        // 先左再根最后右
        traversal(cur->left, v);
        v.push_back(cur->val);
        traversal(cur->right, v);
    }
};

迭代遍历

class Solution {
public:
    vector<int> inorderTraversal(TreeNode* root) {
        vector<int> res;
        if (root == nullptr) return res;

        stack<TreeNode*> st;
        TreeNode* cur = root;
        while (cur || !st.empty()) {
            while (cur != nullptr) { // 有左子树的话，将根结点先入栈
                st.push(cur);
                cur = cur->left;
            }
            // 访问根结点
            cur = st.top(); st.pop();
            res.push_back(cur->val);
            cur = cur->right;
        }
        return res;
    }
};

复杂度分析

空间复杂度：无论是迭代还是递归，都需要用栈来保存节点信息，只不过一个是自己定义的栈，一个是系统栈，因此空间复杂度都为O(n)
时间复杂度：O(n)

[

](https://leetcode-cn.com/problems/binary-tree-tilt/)记住层序遍历，稍微修改一下，就能完成下面道题

102. 二叉树的层序遍历

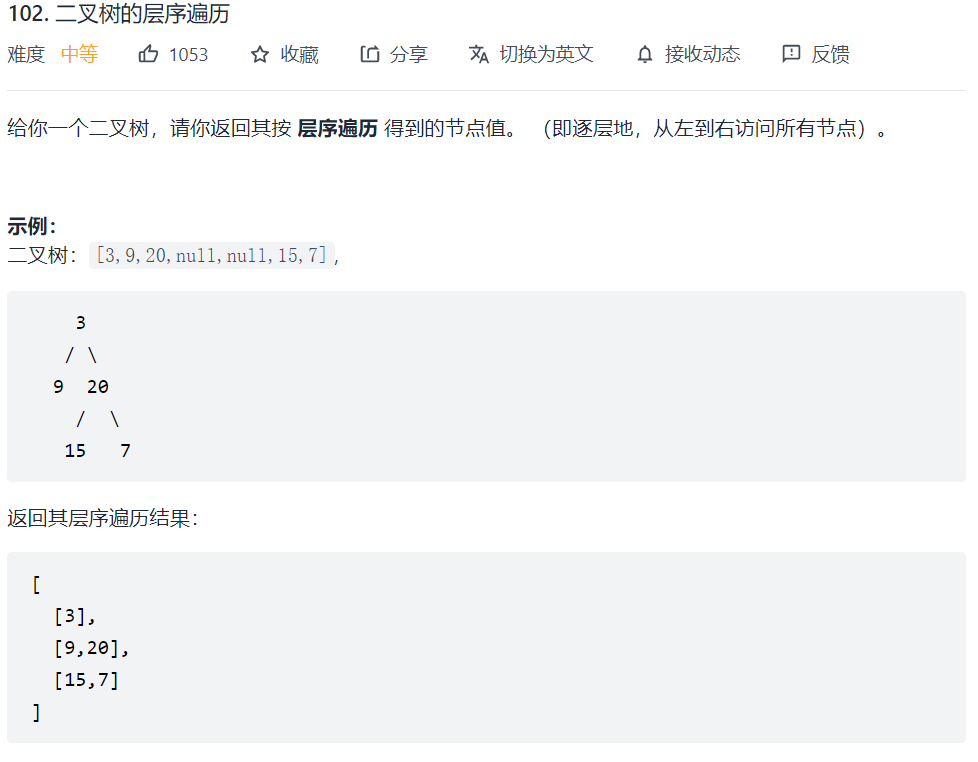
需要借用一个辅助数据结构即队列来实现，队列先进先出，符合一层一层遍历的逻辑，而是用栈先进后出适合模拟深度优先遍历也就是递归的逻辑。

而这种层序遍历方式就是图论中的广度优先遍历，只不过我们应用在二叉树上。
使用队列实现二叉树广度优先遍历，动画如下：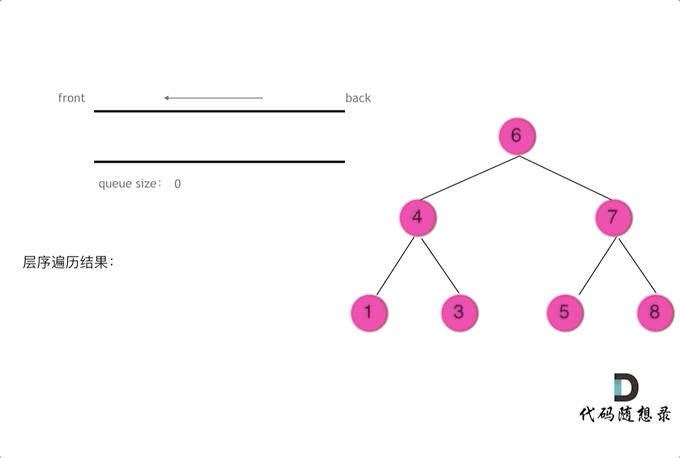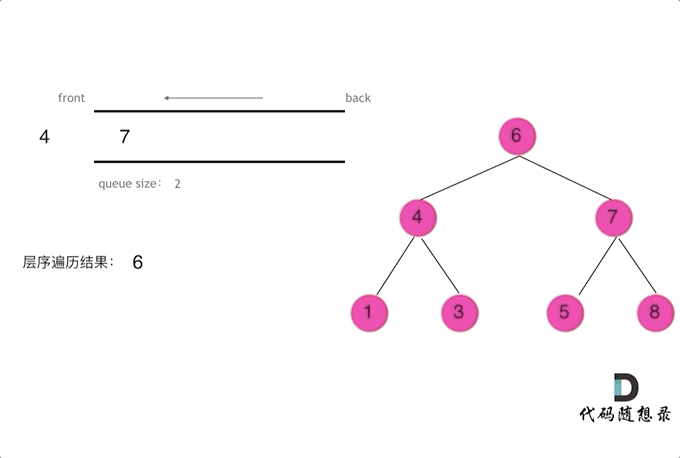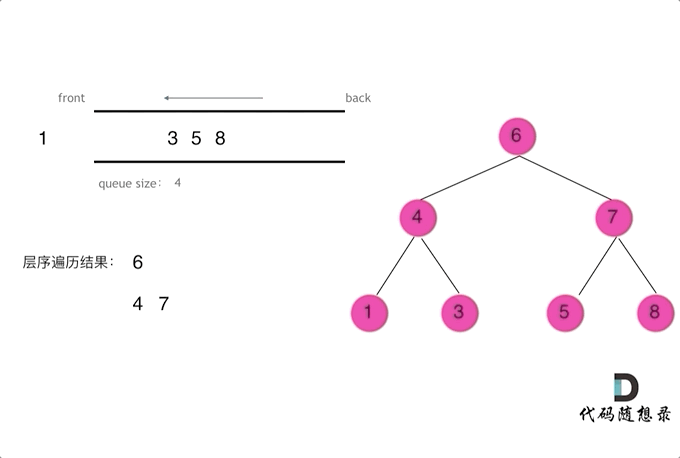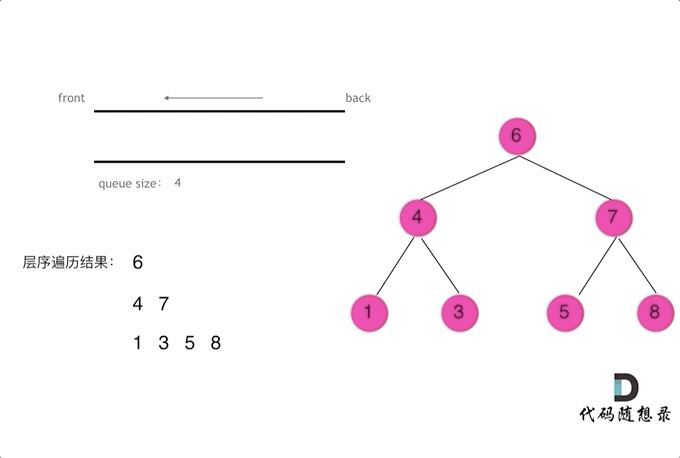

class Solution {
public:
    vector<vector<int>> levelOrder(TreeNode* root) {
        queue<TreeNode*> que;
        vector<vector<int>> res;
        if (root == nullptr) return res;
        que.push(root);
        while (!que.empty()) {
            int size = que.size(); // 当前层的节点个数
            vector<int> level;
            for (int i = 0; i < size; i++) {
                TreeNode* node = que.front();
                que.pop();
                level.push_back(node->val);
                if (node->left != nullptr) que.push(node->left);
                if (node->right != nullptr) que.push(node->right);
            }
            res.push_back(level);
        }
        return res;
    }
};

107. 二叉树的层序遍历 II

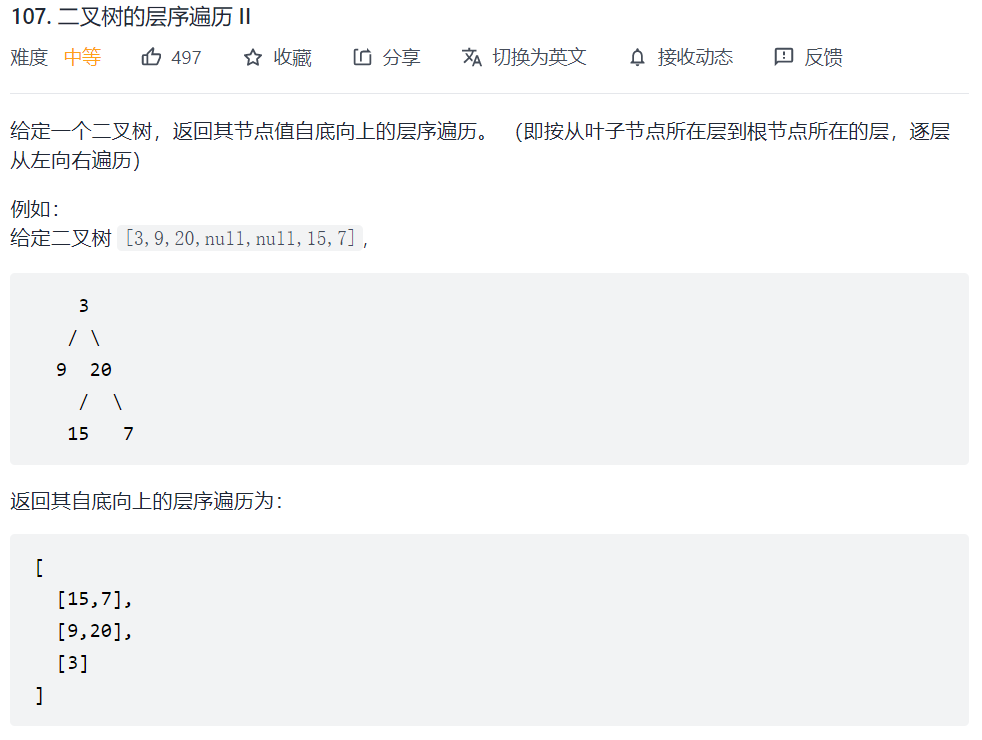
102题是返回从顶层向下的结果，这一题要求返回自底向上的层序遍历结果，那么我们直接对结果进行反转即可。

class Solution {
public:
    vector<vector<int>> levelOrderBottom(TreeNode* root) {
        vector<vector<int>> res;
        if (root == nullptr) return res;
        queue<TreeNode*> que;
        que.push(root);
        while (!que.empty()) {
            int size = que.size();
            vector<int> level;
            for (int i = 0; i < size; i++) {
                TreeNode* node = que.front();
                que.pop();
                level.push_back(node->val);
                if (node->left != nullptr) que.push(node->left);
                if (node->right != nullptr) que.push(node->right);
            }
            res.push_back(level);
        }
        reverse(res.begin(), res.end()); // 反转自顶向下的结果
        return res;
    }
};

199. 二叉树的右视图

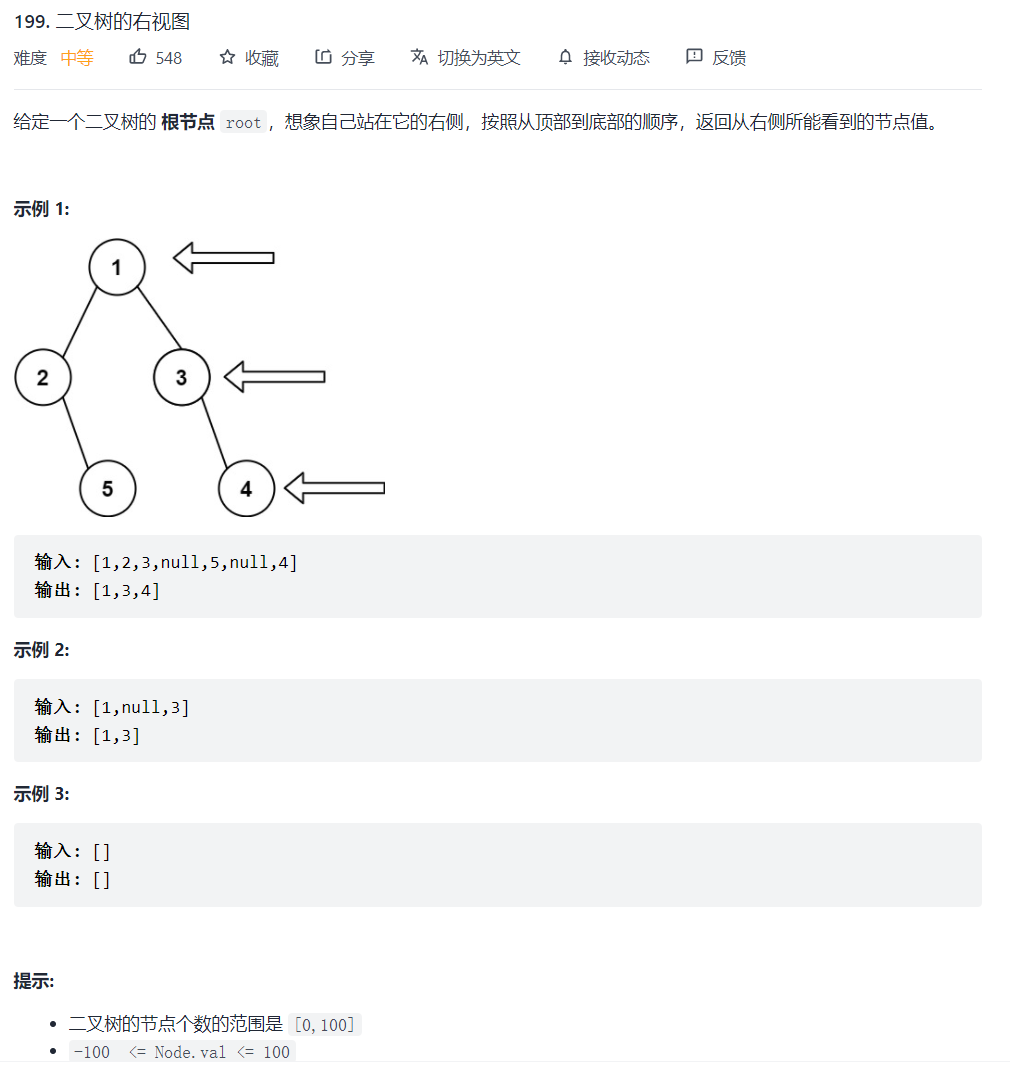
所谓，二叉树的右视图，实际上就是得到每一层的最后一个节点值，因此，在层序遍历的基础上，我们直接把每一层的最后一个元素放入res中。

class Solution {
public:
    vector<int> rightSideView(TreeNode* root) {
        vector<int> res;
        if (root == nullptr) return res;
        queue<TreeNode*> que;
        que.push(root);
        while (!que.empty()) {
            int size = que.size();
            for (int i = 0; i < size; i++) {
                TreeNode* node = que.front();
                que.pop();
                if (i == size - 1)
                    res.push_back(node->val);
                if (node->left != nullptr) que.push(node->left);
                if (node->right != nullptr) que.push(node->right);
            }
        }
        return res;
    }
};

637. 二叉树的层平均值

将层序每一层的结果求个平均值就可。


class Solution {
public:
    vector<double> averageOfLevels(TreeNode* root) {
        vector<double> res;
        if (root == nullptr) return res;
        queue<TreeNode*> que;
        que.push(root);
        while (!que.empty()) {
            int size = que.size();
            double sum = 0;
            for (int i = 0; i < size; i++) {
                TreeNode* node = que.front();
                que.pop();
                sum += node->val;
                if (node->left != nullptr) que.push(node->left);
                if (node->right != nullptr) que.push(node->right);
            }
            res.push_back(sum / size); //保存当前层的平均值
        }
        return res;
    }
};

429. N 叉树的层序遍历

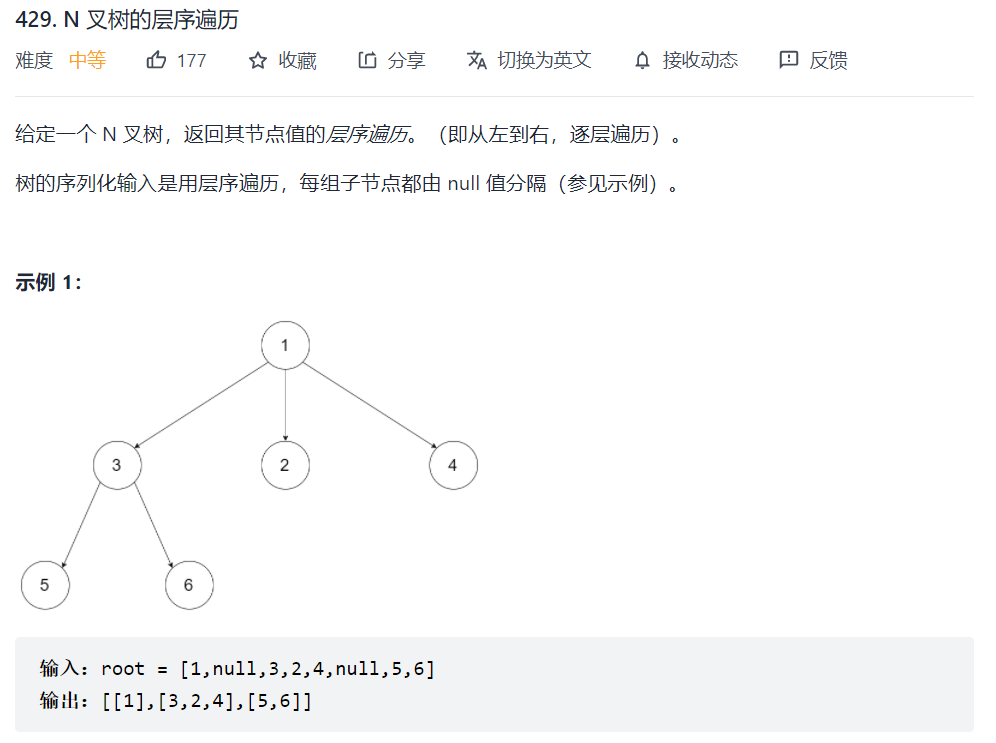
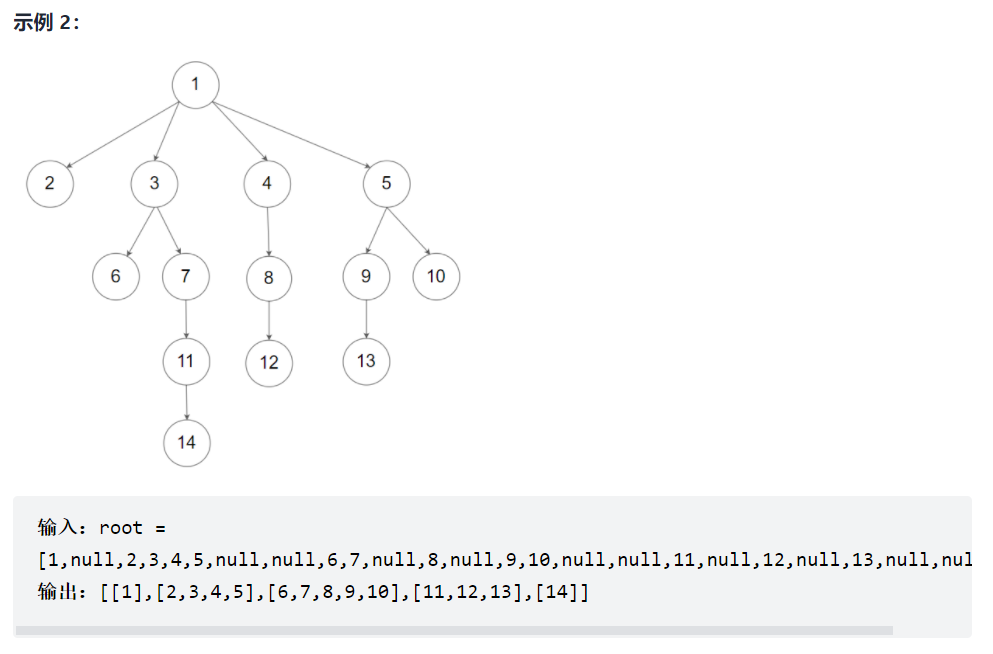
N叉树的定义

/*
// Definition for a Node.
class Node {
public:
    int val;
    vector<Node*> children;

    Node() {}

    Node(int _val) {
        val = _val;
    }

    Node(int _val, vector<Node*> _children) {
        val = _val;
        children = _children;
    }
};
*/

套层序遍历的模板

class Solution {
public:
    vector<vector<int>> levelOrder(Node* root) {
        vector<vector<int>> res;
        if (root == nullptr) return res;
        queue<Node*> que;
        que.push(root);
        while (!que.empty()) {
            int size = que.size();
            vector<int> level;
            for (int i = 0; i < size; i++) {
                Node* node = que.front();
                que.pop();
                level.push_back(node->val);
                // 孩子的数量不确定，用循环
                for (auto child : node->children) {
                    que.push(child);
                }
            }
            res.push_back(level);
        }
        return res;
    }
};

515. 在每个树行中找最大值

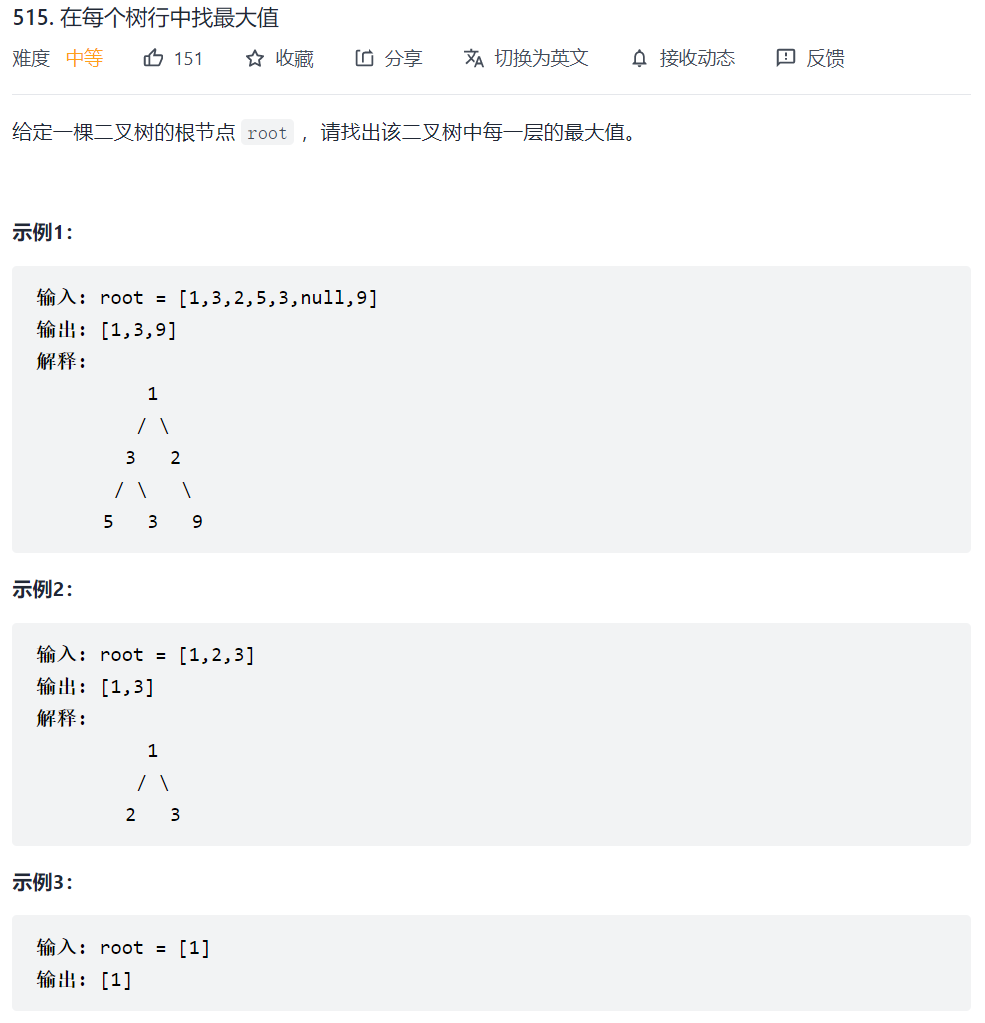
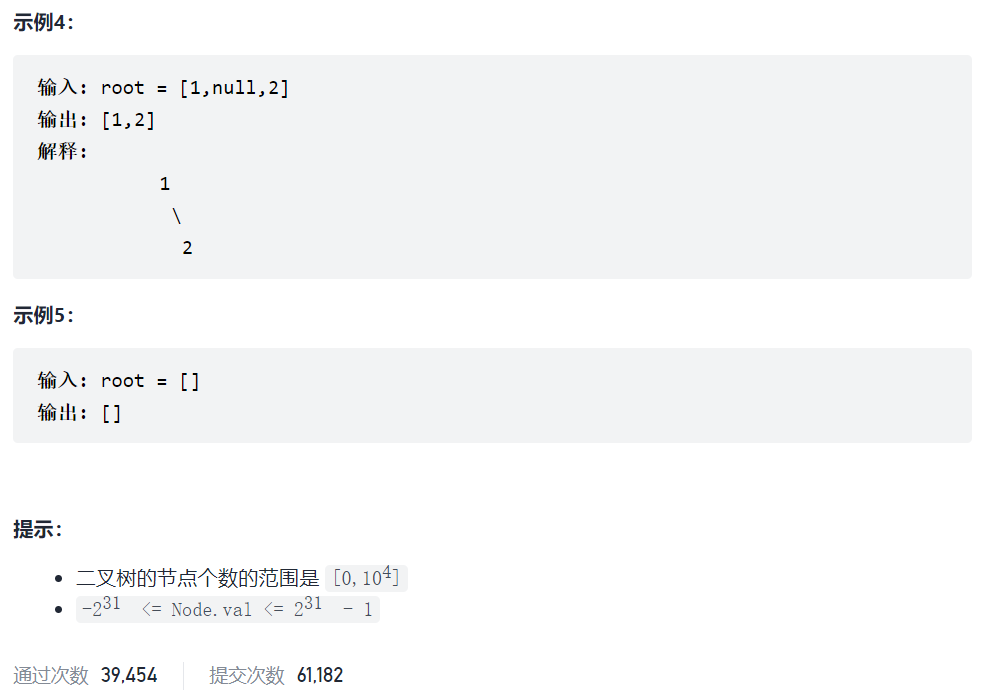
依然套用层序遍历的模板

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    vector<int> largestValues(TreeNode* root) {
        queue<TreeNode*> que;
        vector<int> res;
        if (root == nullptr) return res;
        que.push(root);
        while (!que.empty()) {
            int size = que.size(); // 当前层的节点个数
            int max = INT_MIN; // 记录每层的最大值
            for (int i = 0; i < size; i++) {
                TreeNode* node = que.front();
                que.pop();
                if (node->val > max) max = node->val;
                if (node->left != nullptr) que.push(node->left);
                if (node->right != nullptr) que.push(node->right);
            }
            res.push_back(max);
        }
        return res;
    }
};

116. 填充每个节点的下一个右侧节点指针

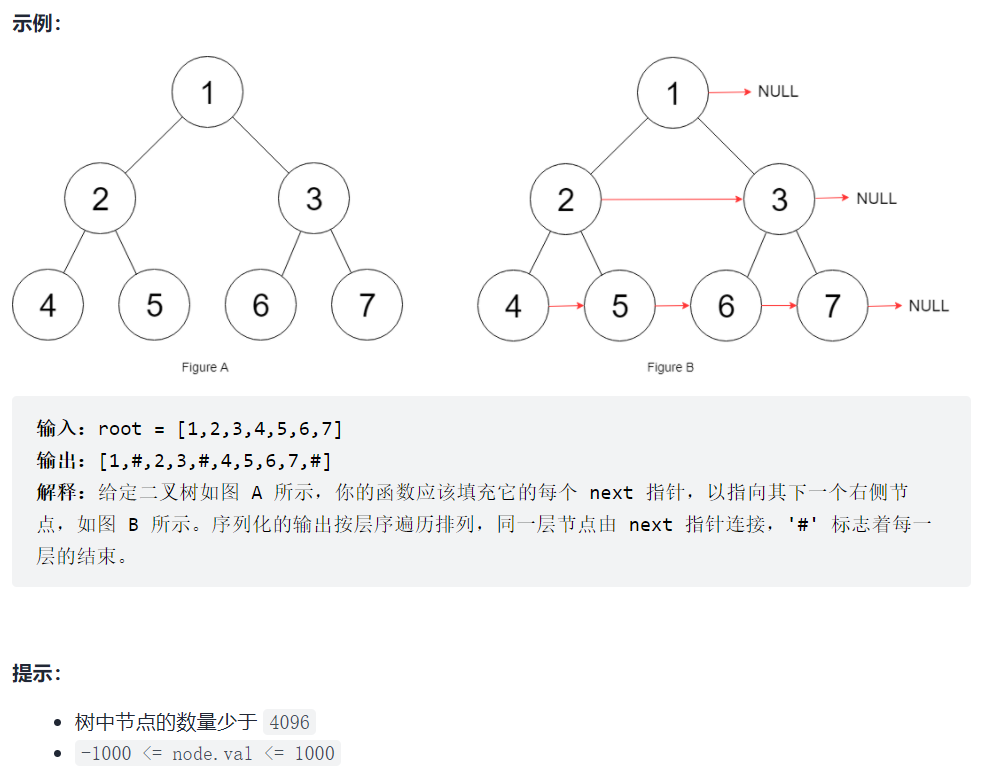
套用层序遍历的模板，遍历每一层元素，如果元素不是最后一个，对其赋值

/*
// Definition for a Node.
class Node {
public:
    int val;
    Node* left;
    Node* right;
    Node* next;

    Node() : val(0), left(NULL), right(NULL), next(NULL) {}

    Node(int _val) : val(_val), left(NULL), right(NULL), next(NULL) {}

    Node(int _val, Node* _left, Node* _right, Node* _next)
        : val(_val), left(_left), right(_right), next(_next) {}
};
*/

class Solution {
public:
    Node* connect(Node* root) {
        if (!root) return root;
        queue<Node*> que;
        que.push(root);
        while (!que.empty()) {
            int size = que.size(); // 当前层的节点个数
            for (int i = 0; i < size; i++) {
                Node* node = que.front();
                que.pop();
                if (i < size - 1) // 不是层的最后一个元素
                    node->next = que.front();
                // 默认next都为null，因此不用再设置最后一个元素的next
                if (node->left) que.push(node->left);
                if (node->right) que.push(node->right);
            }
        }
        return root;
    }
};

117. 填充每个节点的下一个右侧节点指针 II

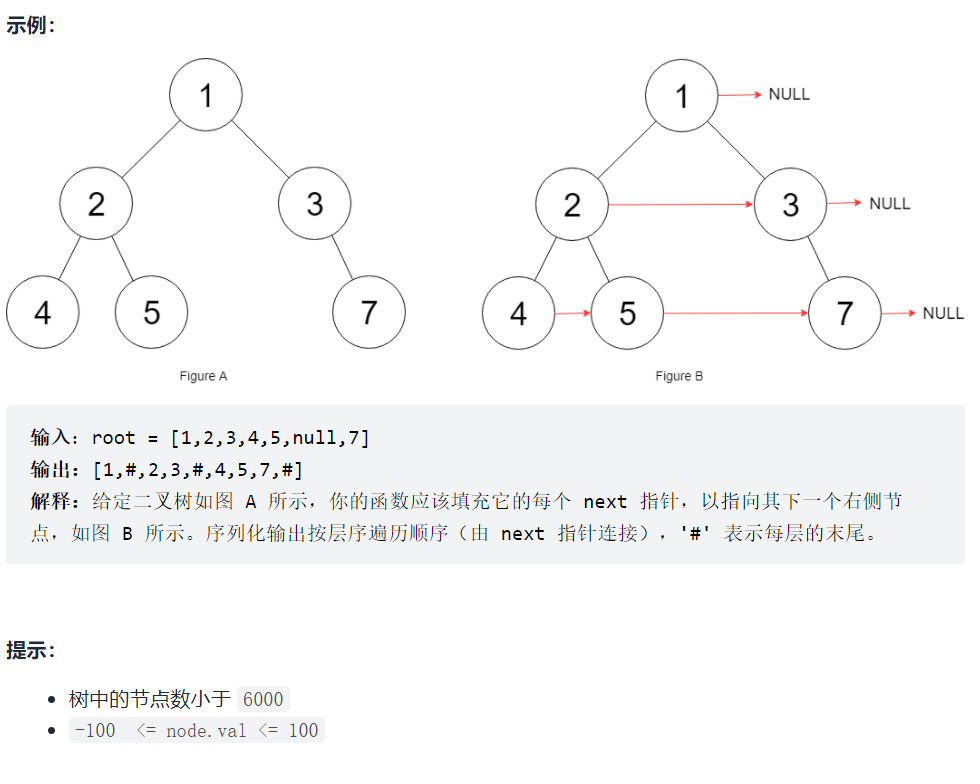
上一道题，使用层序遍历模板的解法，不需要考虑二叉树是否完美，因此，本题代码与上一题一样

class Solution {
public:
    Node* connect(Node* root) {
        if (!root) return root;
        queue<Node*> que;
        que.push(root);
        while (!que.empty()) {
            int size = que.size(); // 当前层的节点个数
            for (int i = 0; i < size; i++) {
                Node* node = que.front();
                que.pop();
                if (i < size - 1) // 不是层的最后一个元素
                    node->next = que.front();
                // 默认next都为null，因此不用再设置最后一个元素的next
                if (node->left) que.push(node->left);
                if (node->right) que.push(node->right);
            }
        }
        return root;
    }
};

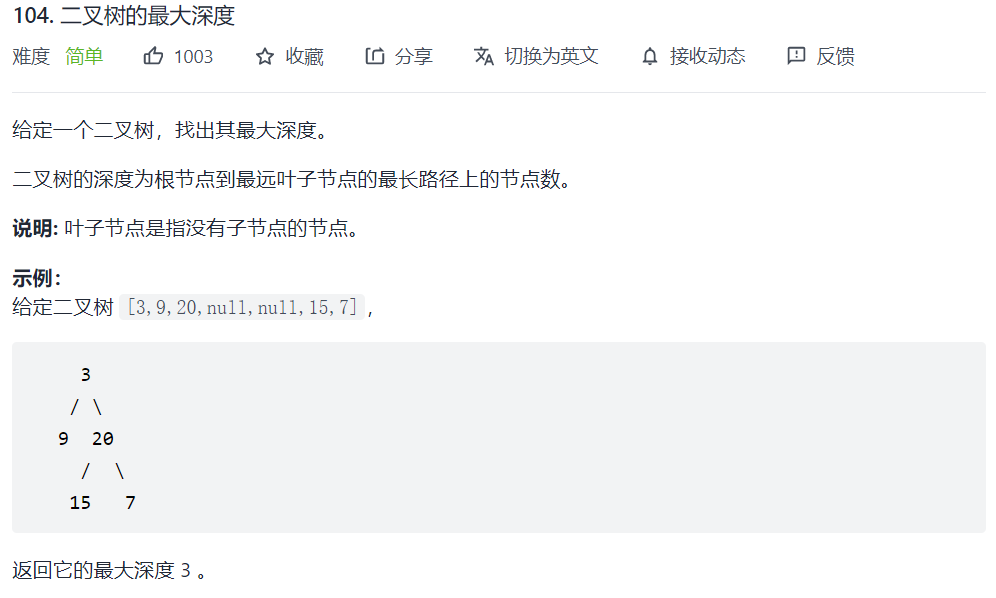
104. 二叉树的最大深度

思路一：广度优先

套用层序遍历的模板

class Solution {
public:
    int maxDepth(TreeNode* root) {
        queue<TreeNode*> que;
        int depth = 0;
        if (root == nullptr) return depth;
        que.push(root);
        while (!que.empty()) {
            int size = que.size(); // 当前层的节点个数
            depth++; // 记录深度
            for (int i = 0; i < size; i++) {
                TreeNode* node = que.front();
                que.pop();
                if (node->left != nullptr) que.push(node->left);
                if (node->right != nullptr) que.push(node->right);
            }

        }
        return depth;
    }
};

思路二：深度优先

知道了左右子树的最大深度，那么树的最大深度就是左右子树的最大深度之中最大的那个+1

class Solution {
public:
    int maxDepth(TreeNode* root) {
        if(!root) return 0;
        return max(maxDepth(root->left), maxDepth(root->right)) + 1;
    }
};

通过递归三部曲更加深刻的理解这个深度优先方法：
精简的写法看不出这道题是先序遍历还是后续遍历：

先序遍历求的是深度
后序遍历求的是高度，根节点的高度就是树的深度

使用后序遍历计算树的高度：

确定递归函数的参数和返回值：参数就是传入树的根节点，返回就返回这棵树的深度，所以返回值为int类型。
```
int getdepth(treenode* node)
```
确定终止条件：如果节点为空的话，返回0，表示高度为0
```
if (!node) return 0;
```

确定单层递归的逻辑：先求它的左子树的深度，再求的右子树的深度，最后取左右深度最大的数值再+1 （加1是因为算上当前中间节点）就是目前节点为根节点的树的深度

int leftdepth = getdepth(node->left);       // 左
int rightdepth = getdepth(node->right);     // 右
int depth = 1 + max(leftdepth, rightdepth); // 中
return depth;

整体代码如下：

class solution {
public:
 int getdepth(treenode* node) {
     if (node == null) return 0;
     int leftdepth = getdepth(node->left);       // 左
     int rightdepth = getdepth(node->right);     // 右
     int depth = 1 + max(leftdepth, rightdepth); // 中
     return depth;
 }
 int maxdepth(treenode* root) {
     return getdepth(root);
 }
};

代码精简后就是最开始的代码了！！！

使用前序遍历的话，就能体现出回溯的过程

class solution {
public:
    int result;
    void getdepth(treenode* node, int depth) {
        result = depth > result ? depth : result; // 中

        if (node->left == null && node->right == null) return ;

        if (node->left) { // 左
            depth++;    // 深度+1
            getdepth(node->left, depth);
            depth--;    // 回溯，深度-1
        }
        if (node->right) { // 右
            depth++;    // 深度+1
            getdepth(node->right, depth);
            depth--;    // 回溯，深度-1
        }
        return ;
    }
    int maxdepth(treenode* root) {
        result = 0;
        if (root == 0) return result;
        getdepth(root, 1);
        return result;
    }
};

精简后：

class solution {
public:
    int result;
    void getdepth(treenode* node, int depth) {
        result = depth > result ? depth : result; // 中
        if (node->left == null && node->right == null) return ;
        if (node->left) { // 左
            getdepth(node->left, depth + 1);
        }
        if (node->right) { // 右
            getdepth(node->right, depth + 1);
        }
        return ;
    }
    int maxdepth(treenode* root) {
        result = 0;
        if (root == 0) return result;
        getdepth(root, 1);
        return result;
    }
};

559. N 叉树的最大深度

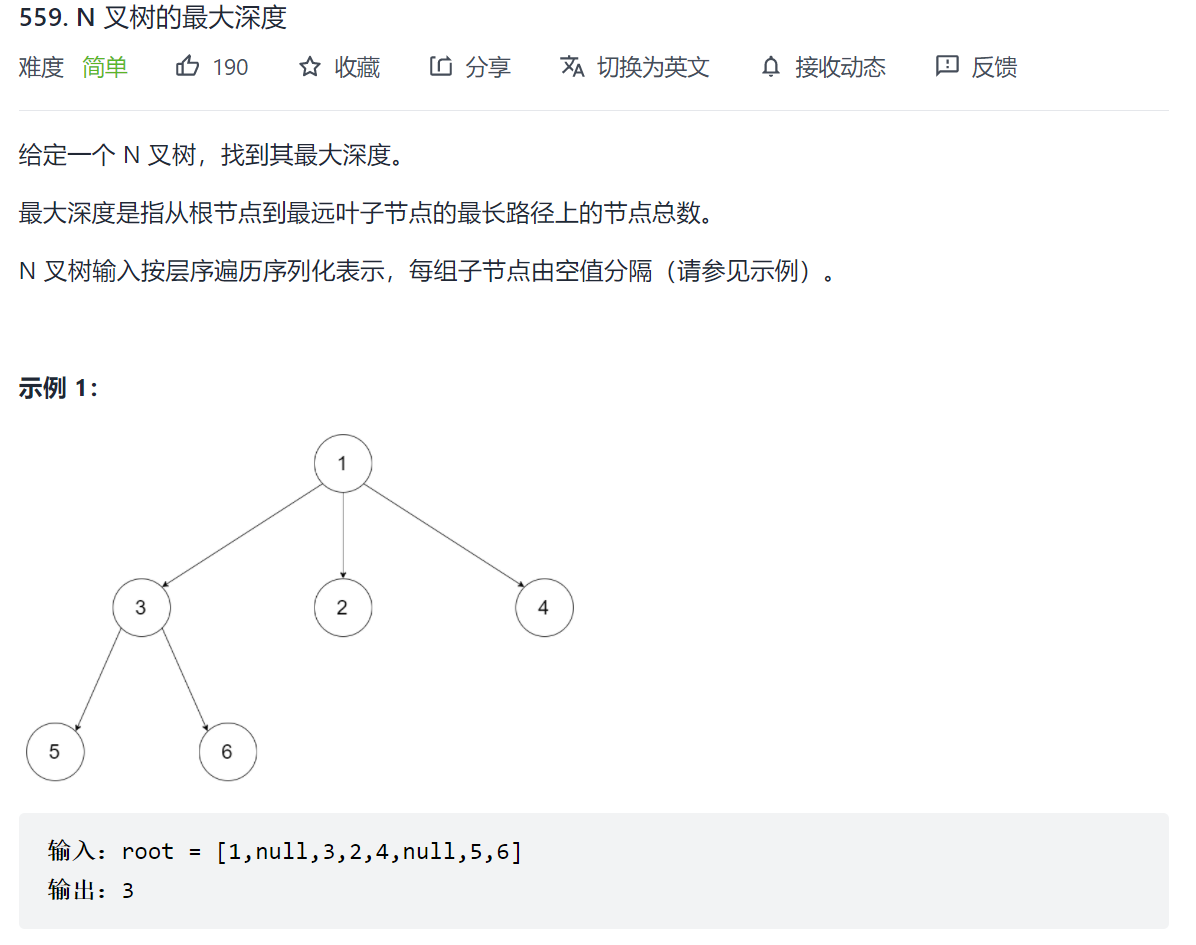
N叉树的定义如下：

// Definition for a Node.
class Node {
public:
    int val;
    vector<Node*> children;

    Node() {}

    Node(int _val) {
        val = _val;
    }

    Node(int _val, vector<Node*> _children) {
        val = _val;
        children = _children;
    }
};

递归法

确定参数和返回值：参数为节点，返回值为int
```
int getDepth(Node* root)
```
确定递归出口：如果节点为空的话，返回0
```
if (!root) return 0;
```

确定单层递归的逻辑：求每个子树的高度，树的高度为最大的子树高度加1

int maxdep = 0;
for (auto node : root->children) {
 maxdep = max(maxdep, getDepth(node));
}
return maxdep + 1;

完整代码如下：

class Solution {
public:
 int maxDepth(Node* root) {
     return getDepth(root);
 }
 int getDepth(Node* root) {
     if (!root) return 0;
     int maxdep = 0;
     for (auto node : root->children) {
         maxdep = max(maxdep, getDepth(node));
     }
     return maxdep + 1;
 }
};

简化后的代码如下：

class Solution {
public:
 int maxDepth(Node* root) {
     if (!root) return 0;
     int maxdep = 0;
     for (auto node : root->children) {
         maxdep = max(maxdep, maxDepth(node));
     }
     return maxdep + 1;
 }
};

迭代法

使用层序遍历的模板，稍微修改下即可
代码如下：

class Solution {
public:
 int maxDepth(Node* root) {
     if (!root) return 0;
     queue<Node*> que;
     que.push(root);
     int depth = 0;
     while (!que.empty()) {
         depth++;
         int size = que.size();
         for (int i = 0; i < size; i++) {
             Node* node = que.front(); que.pop();
             for (auto n : node->children) {
                 que.push(n);
             }
         }
     }
     return depth;
 }
};

111. 二叉树的最小深度

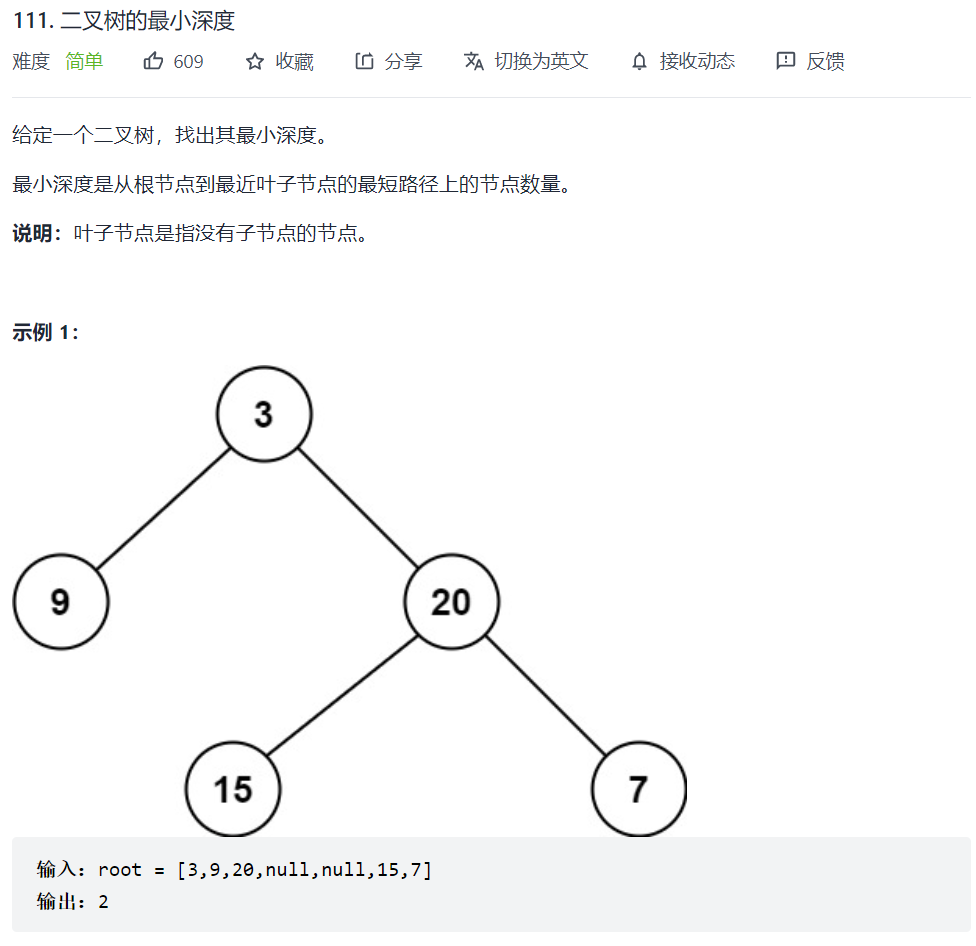
这道题要注意的一点就是，只有当一个节点左孩子和右孩子都不存在时，这个节点才是叶子节点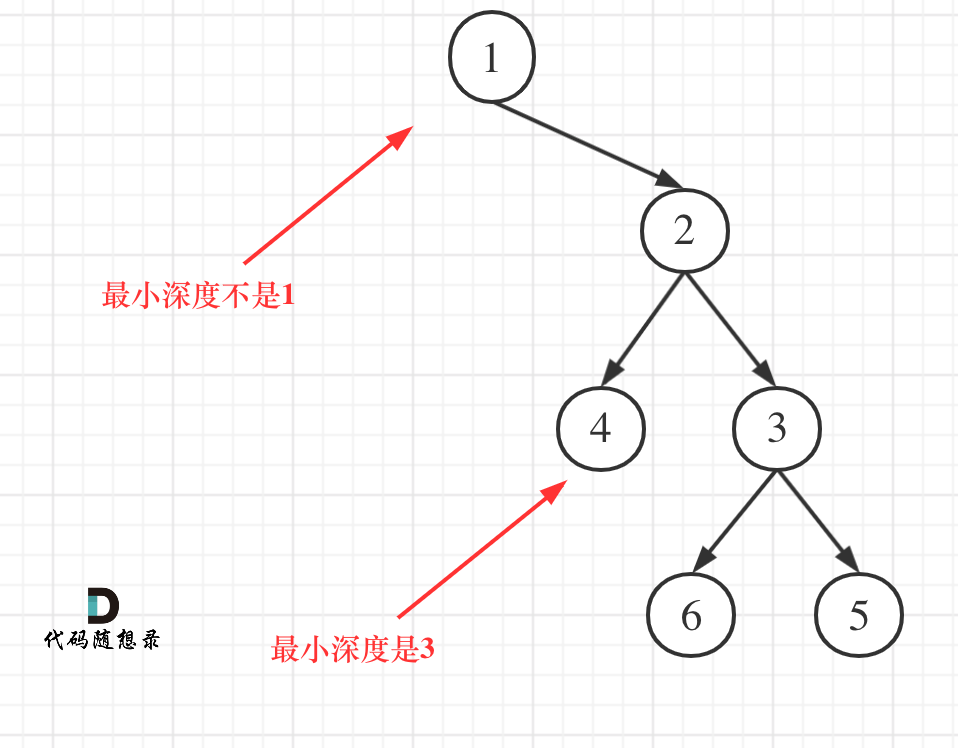

思路一：广度优先

套用层序遍历的模板，在最大深度的基础上，加一个判断条件，如果出队时某节点是叶子节点，那么返回当前深度。

class Solution {
public:
    int minDepth(TreeNode* root) {
        queue<TreeNode*> que;
        int depth = 0;
        if (root == nullptr) return depth;
        que.push(root);
        while (!que.empty()) {
            int size = que.size(); // 当前层的节点个数
            depth++; // 记录深度
            for (int i = 0; i < size; i++) {
                TreeNode* node = que.front();
                que.pop();
                if (!node->left && !node->right)//当前节点为叶子节点，返回当前深度
                    return depth;
                if (node->left != nullptr) que.push(node->left);
                if (node->right != nullptr) que.push(node->right);
            }
        }
        return depth;
    }
};

思路二：深度优先

对于每个非叶子节点，都可以考虑其左子树和右子树的最小叶子结点深度，那么就可以递归的解决这个问题

class Solution {
public:
    int minDepth(TreeNode* root) {
        if (root == nullptr) return 0;
        if (root->left != nullptr && root->right == nullptr) {
            return minDepth(root->left) + 1;
        }
        if (root->left == nullptr && root->right != nullptr) {
            return minDepth(root->right) + 1;
        }
        return min(minDepth(root->left), minDepth(root->right)) + 1;
    }
};

或

class Solution {
public:
    int minDepth(TreeNode* root) {
        if (!root) return 0;
        else if (!root->left) return minDepth(root->right) + 1;
        else if (!root->right) return minDepth(root->left) + 1;
        else return min(minDepth(root->left), minDepth(root->right)) + 1;
    }
};

[

](https://leetcode-cn.com/problems/binary-tree-tilt/)