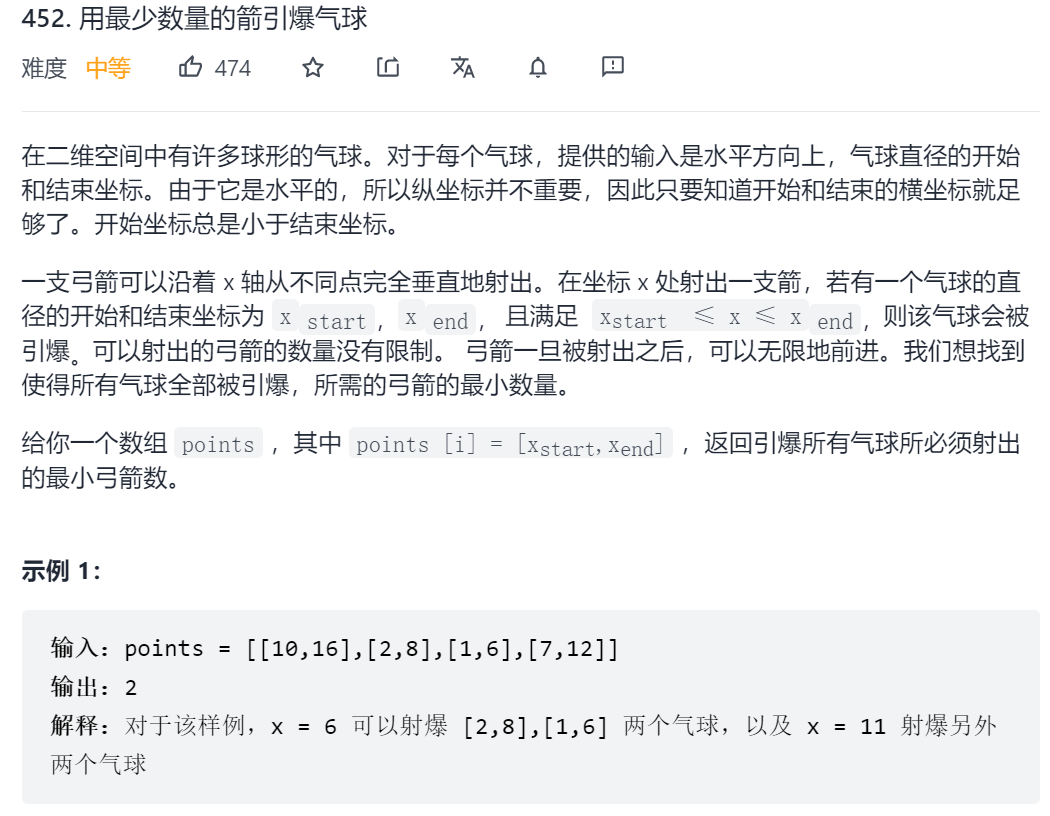
452. 用最少数量的箭引爆气球">452. 用最少数量的箭引爆气球
- 思路一：按左边界排序，寻找最小右边界
- 思路二：按右边界排序
55. 跳跃游戏">55. 跳跃游戏
45. 跳跃游戏 II">45. 跳跃游戏 II
435. 无重叠区间">435. 无重叠区间
763. 划分字母区间">763. 划分字母区间
56. 合并区间">56. 合并区间

452. 用最少数量的箭引爆气球

思路一：按左边界排序，寻找最小右边界

用更少的箭，射爆更多的气球，就是尽可能的让有重叠区间的气球，被一只箭射爆，那么可以对区间进行排序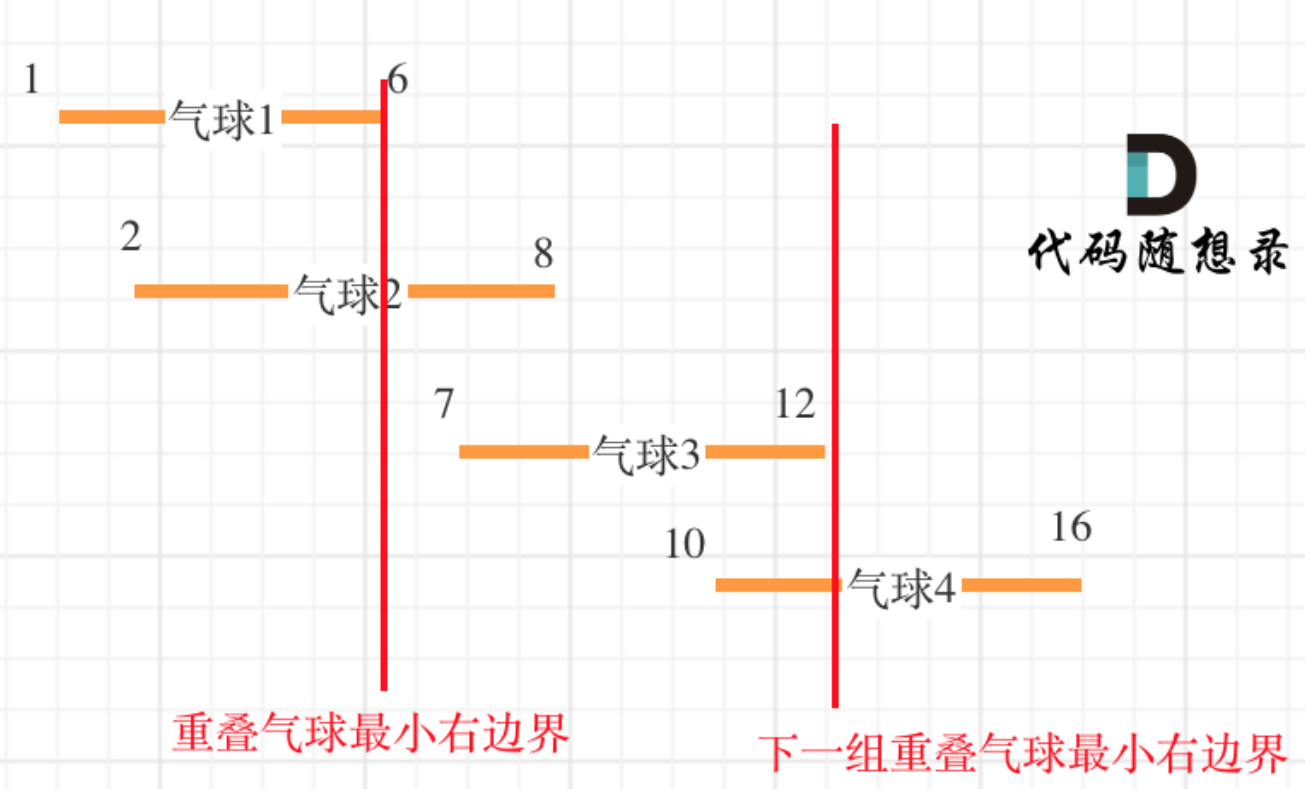

遍历区间，如果当前区间的左端点小于上一个区间（重叠区间的最小右边界），那么这支箭可以同时射爆这个🎈，需要更新最小有边界；如果大于最小右边界，则需要增加一支箭

class Solution {
public:
    int findMinArrowShots(vector<vector<int>>& points) {
        if (points.size() == 0) return 0;
        int result = 1; // 气球不为0，最少需要一只箭
        sort(points.begin(), points.end(), [](vector<int>& v1, vector<int>& v2){
            return v1[0] < v2[0];
        });
        for (int i = 1; i < points.size(); i++) {
            if (points[i][0] > points[i - 1][1]) { // 不重叠，加一支箭
                result++;
            } else { // 有重叠，更新重叠气球的最小右边界
                points[i][1] = min(points[i][1], points[i - 1][1]);
            }
        }
        return result;
    }
};

思路二：按右边界排序

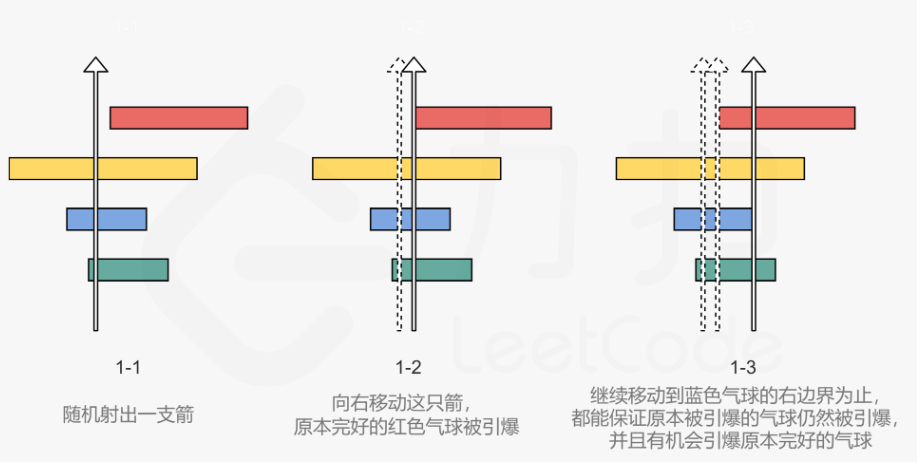
class Solution {
public:
    int findMinArrowShots(vector<vector<int>>& points) {
        if (points.empty()) return 0;
        sort(points.begin(), points.end(), [](const auto& v1, const auto& v2) {
            return v1[1] < v2[1];
        });
        int right = points[0][1]; // 这支箭能够射爆的所有气球的最小右边界
        int res = 1;
        for (const auto& point : points) {
            if (point[0] > right) {
                res++;
                right = point[1];
            }
        }
        return res;
    }
};

55. 跳跃游戏

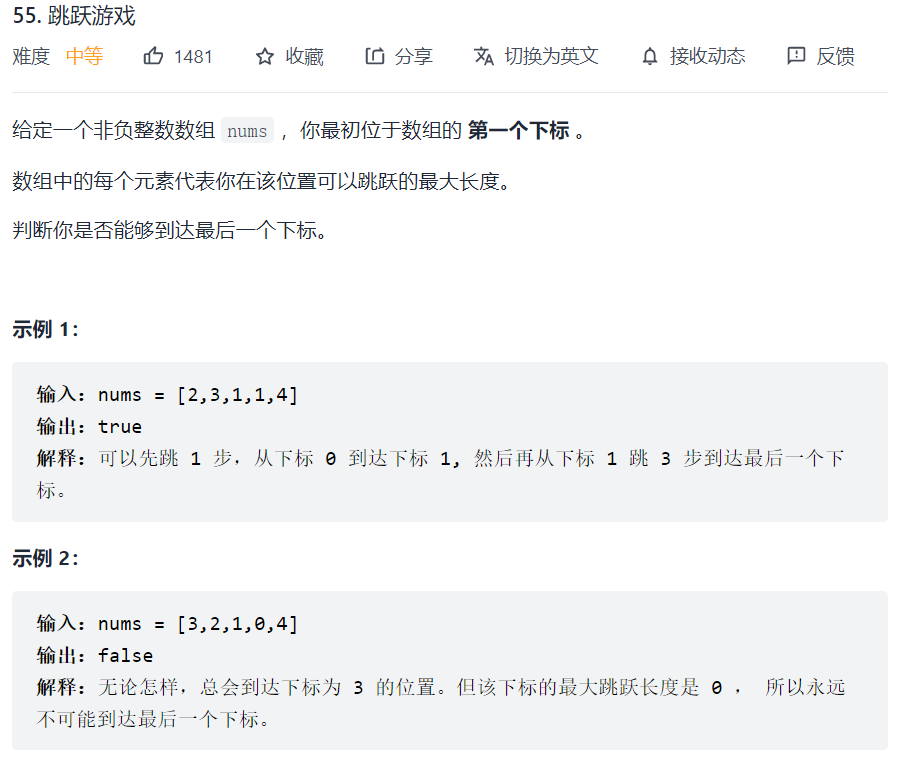
本题跳几步无所谓，关键在于可跳的覆盖范围！
不用明确具体每次跳几步，只需要每次根据最大可跳跃的步数来确定目前最大可达范围，如果范围能够达到最后一个位置，那么返回true。这个范围内，别管是怎么跳的，反正一定可以跳过来。
那么这个问题就转化为跳跃覆盖范围究竟可不可以覆盖到终点！
每次移动取最大跳跃步数（得到最大的覆盖范围），每移动一个单位，就更新最大覆盖范围。
贪心算法局部最优解：每次取最大跳跃步数（取最大覆盖范围），整体最优解：最后得到整体最大覆盖范围，看是否能到终点。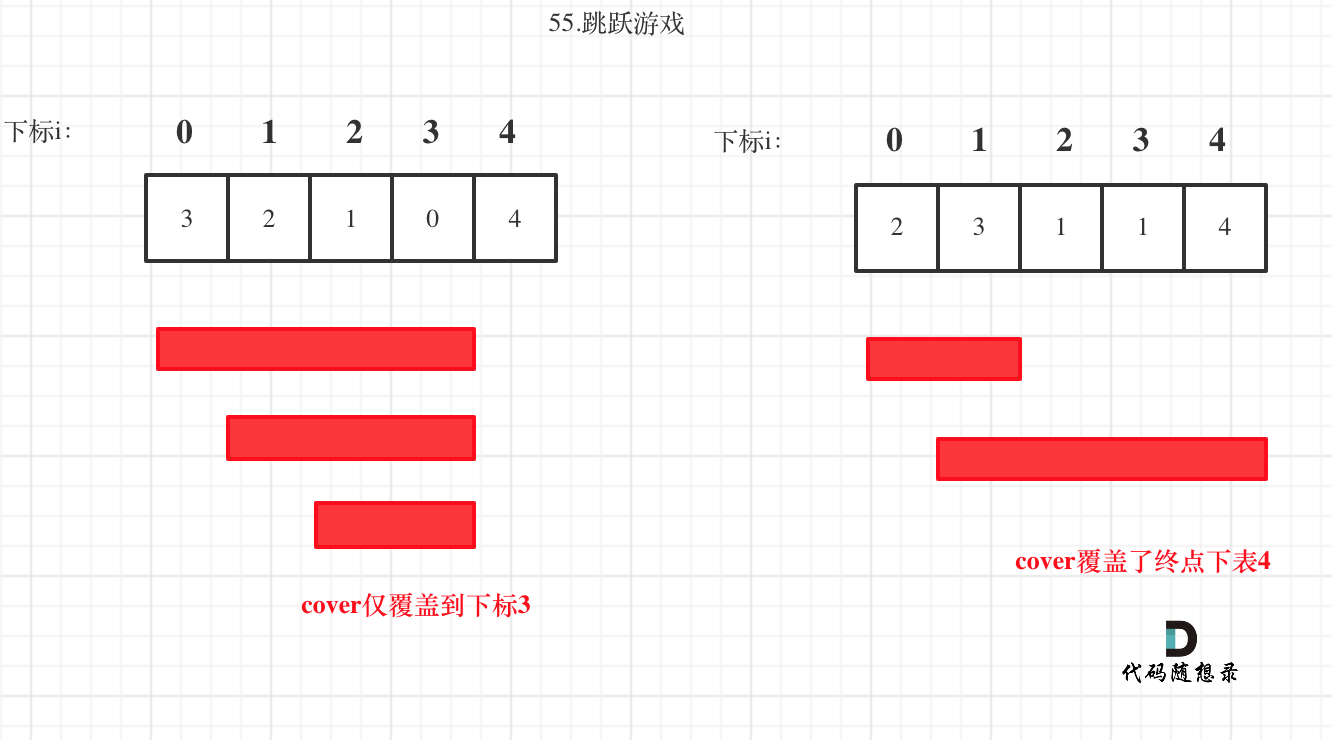

class Solution {
public:
    bool canJump(vector<int>& nums) {
        int maxRange = 0;
        for (int i = 0; i <= maxRange; i++) { // 只可以在最大可达范围内蹦跶
            maxRange = max(i + nums[i], maxRange);
            if (maxRange >= nums.size() - 1) return true;
        }
        return false;
    }
};

45. 跳跃游戏 II

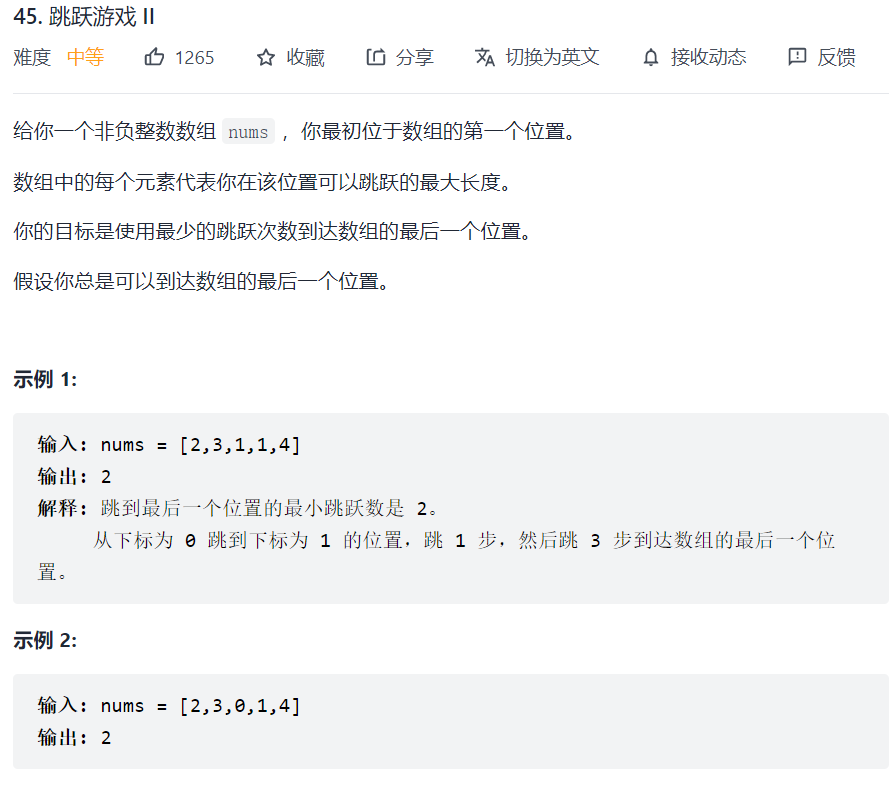
维护两个变量，当前次跳跃可以达到的最远位置，可以达到的远位置，遍历数组元素，更新可以达到的最远位置，如果当前处于最远位置，那么增加一次跳跃，同时更新当前跳跃次数可以达到的最远位置

在遍历数组时，不访问最后一个元素，这是因为在访问最后一个元素之前，我们的边界一定大于等于最后一个位置，否则就无法跳到最后一个位置了。（题目说了，总能到达最后一个位置）如果访问最后一个元素，在边界正好为最后一个位置的情况下，我们会增加一次「不必要的跳跃次数」，因此我们不必访问最后一个元素。

class Solution {
public:
    int jump(vector<int>& nums) {
        int n = nums.size(), maxRange = 0, range = 0, res = 0;
        for (int i = 0; i < n - 1; i++) {
            maxRange = max(maxRange, i + nums[i]);
            if (i == range) { // 达到这几次跳跃能够到达的最远位置
                res++;
                range = maxRange;
            }
        }
        return res;
    }
};

两个思路其实贪心策略是一样的，就是考虑每一次跳跃能到达的最远位置，只不过思路二通过控制循环的条件，来简化了代码

复杂度分析：

时间复杂度O(N)
空间复杂度O(1)
435. 无重叠区间

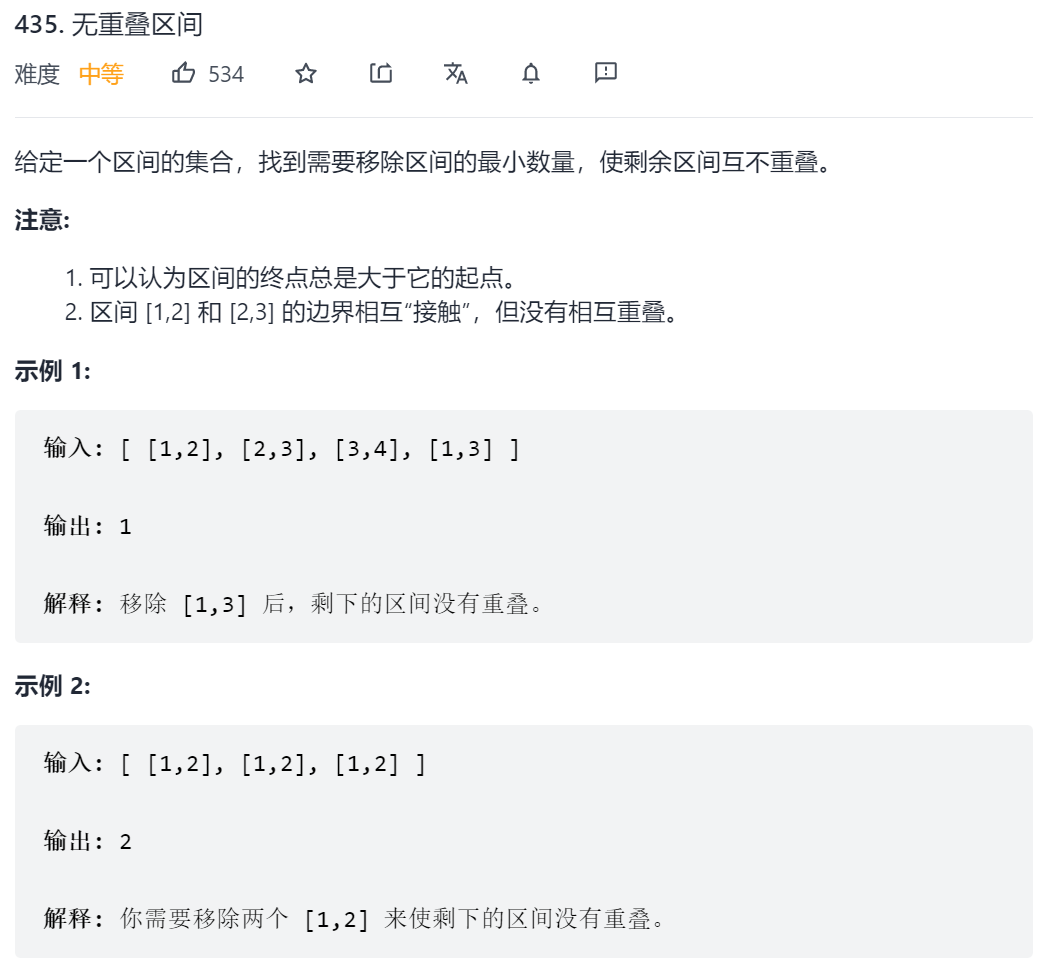
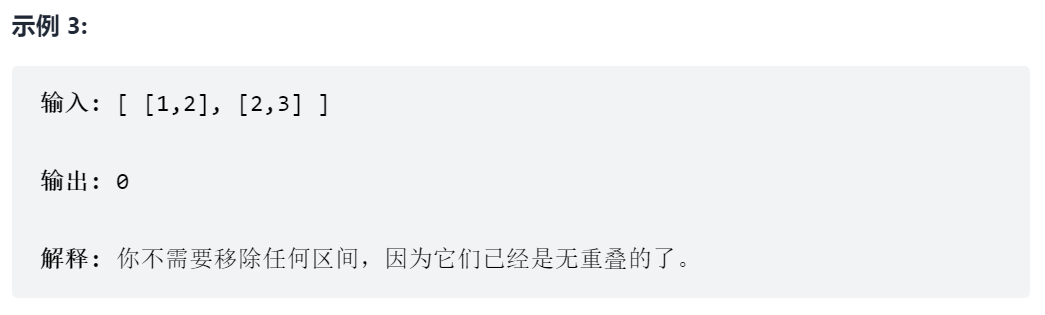
解决区间问题一般都需要进行排序，对于452题引爆气球来说，需要尽可能地令区间重叠，可以根据区间的左端点排序，区间的右端点越大，越容易和更多的区间重叠。对于这道题来说，要尽量让区间无重叠，那么可以根据区间的右端点排序，右端点越小，留给其它区间的位置就越多，因此采取的贪心策略为，优先保留结尾小且不相交的区
间。

用一个变量来存储前一个区间的右端点：

class Solution {
public:
    int eraseOverlapIntervals(vector<vector<int>>& intervals) {
        if (intervals.empty()) {
            return 0;
        }
        int n = intervals.size();
        sort(intervals.begin(), intervals.end(), [](vector<int> a, vector<int> b) {
            return a[1] < b[1];
        });
        int total = 0, prev = intervals[0][1];
        for (int i = 1; i < n; ++i) {
            if (intervals[i][0] < prev) {
                // 有重叠，删除这个区间
                ++total;
            } else {
                prev = intervals[i][1];
            }
        }
        return total;
    }
};

或者直接更新intervals

class Solution {
public:
    int eraseOverlapIntervals(vector<vector<int>>& intervals) {
        if (intervals.empty()) return 0;
        sort(intervals.begin(), intervals.end(), [](vector<int>& v1, vector<int>& v2) {
            return v1[1] < v2[1];
        });
        int res = 0;
        for(int i = 1; i < intervals.size(); i++) {
            if (intervals[i][0] < intervals[i - 1][1]) {
                res++;
                intervals[i][1] = intervals[i - 1][1];
            }
        }
        return res;
    }
};

当然，这一题也可以按区间左端点排序，然后从右向左遍历也是可以的。

时间复杂度：O(nlogn) ，有一个快排
空间复杂度：O(1)

换一个问法：统计非交叉区间的个数
判断上一个区间的右端点是否小于等于下一个区间的左端点即可

class Solution {
public:
    // 按照区间右边界排序
    static bool cmp (const vector<int>& a, const vector<int>& b) {
        return a[1] < b[1];
    }
    int eraseOverlapIntervals(vector<vector<int>>& intervals) {
        if (intervals.size() == 0) return 0;
        sort(intervals.begin(), intervals.end(), cmp);
        int count = 1; // 记录非交叉区间的个数
        int end = intervals[0][1]; // 记录区间分割点
        for (int i = 1; i < intervals.size(); i++) {
            if (end <= intervals[i][0]) {
                end = intervals[i][1];
                count++;
            }
        }
        return count;
    }
};

763. 划分字母区间

区间内所有字母出现的最远位置就是当前分割的位置，可以用哈希表来记录每个字母出现的最远位置，然后遍历字符串s，不断更新当前区间内字母出现的最远位置，如果遍历到最远位置，说明从下一个字符开始，都是新的字符，记录当前区间的长度。

可以分为如下两步：

统计每一个字符最后出现的位置
从头遍历字符，并更新字符的最远出现下标，如果找到字符最远出现位置下标和当前下标相等了，则找到了分割点

class Solution {
public:
    vector<int> partitionLabels(string s) {
        int h[26];
        for (int i = 0; i < s.size(); i++) h[s[i] - 'a'] = i;
        int right = 0, left = 0;
        vector<int> res;
        for (int i = 0; i < s.size(); i++) {
            right = max(right, h[s[i] - 'a']);
            if (i == right) {
                res.push_back(right - left + 1);
                left = i + 1; 
            }
        }
        return res;
    }
};

56. 合并区间

先按左边界排序，然后正向遍历intervals，

如果当前记录重叠区间的右端点大于等于当前区间的左端点，说明区间发生重叠，这时候需要更新重叠区间的右边界（取最大值）
如果当前记录重叠区间的右端点小于等于当前区间的左端点，说明区间没有重叠，将记录的重叠区间保存，然后将重叠区间的左右边界更新为当前区间的左右边界，continue

class Solution {
public:
    vector<vector<int>> merge(vector<vector<int>>& intervals) {
        vector<vector<int>> res;
        sort(intervals.begin(), intervals.end(), [](auto& v1, auto& v2) {
            return v1[0] < v2[0];
        });
        res.push_back({intervals[0][0], intervals[0][1]});
        int idx = 0;
        for (int i = 1; i < intervals.size(); i++) {
            if (intervals[i][0] <= res[idx][1]) { // 有重叠则合并
                res[idx][1] = max(res[idx][1], intervals[i][1]);
            } else { // 无重叠则保存
                res.push_back(intervals[i]);
                idx++;
            }
        }
        return res;
    }
};

按右端点排序反向遍历也可以，如果按照右端点排序，正向遍历，如果后面一个区间的左端点比前面的都小就寄了。

区间问题