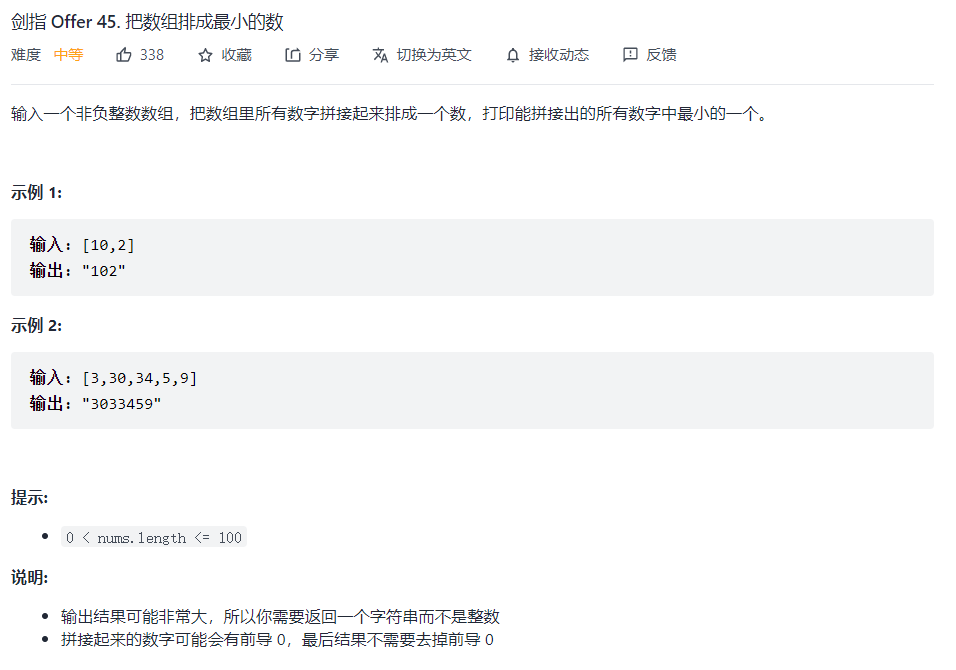
剑指 Offer 45. 把数组排成最小的数

image.png
以 3 、 30 为例
30 3 < 3 30
所以应该将30置于3的前面

  1. class Solution {
  2. public:
  3.     string minNumber(vector<int>& nums) {
  4.         vector<string> strs;
  5.         for (auto &num : nums) {
  6.             strs.push_back(to_string(num));
  7.         }
  8.         sort(strs.begin(), strs.end(), [](const string &a, const string& b){
  9.             return a + b < b + a;
  10.         });
  11.         string res;
  12.         for (auto &str : strs) {
  13.             res += str;
  14.         }
  15.         return res;
  16.     }
  17. };

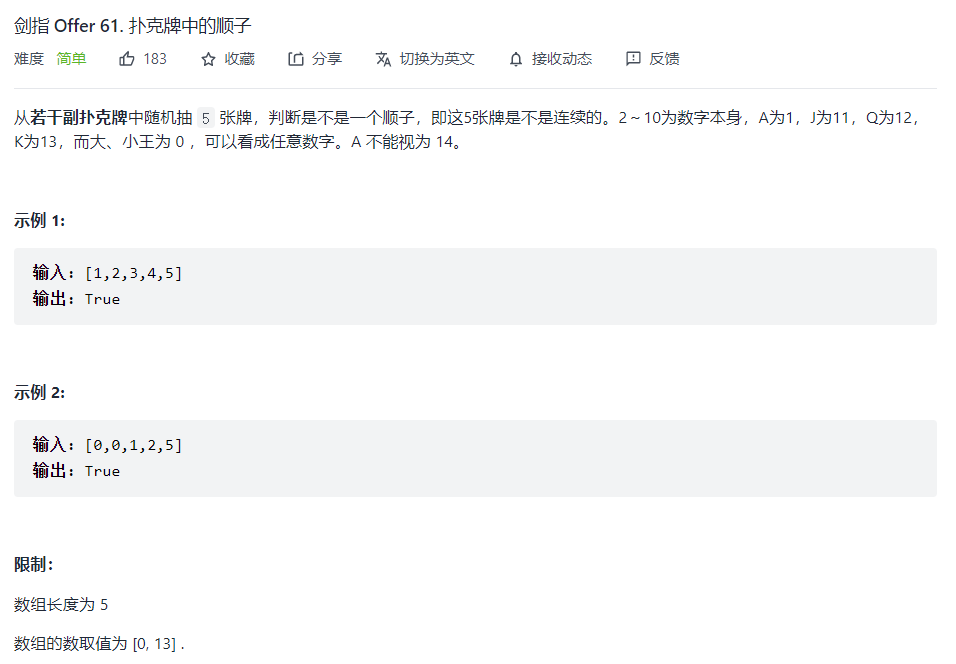
剑指 Offer 61. 扑克牌中的顺子

image.png
image.png

排序

  1. class Solution {
  2. public:
  3.     bool isStraight(vector<int>& nums) {
  4.         sort(nums.begin(), nums.end());
  5.         int joker = 0; // 大小王的数量
  6.         for (int i = 0; i < 4; i++) {
  7.             if (nums[i] == 0) {
  8.                 joker++;
  9.             } else if (nums[i] == nums[i + 1]){
  10.                 return false;
  11.             }
  12.         }
  13.         return nums[4] - nums[joker] < 5; // 最大数减去最小数是否小于五
  14.     }
  15. };

image.png

集合

  1. class Solution {
  2. public:
  3.     bool isStraight(vector<int>& nums) {
  4.         unordered_set<int> us;
  5.         int maxNum = 0, minNum = 100;
  6.         for (const auto &num : nums) {
  7.             if (num == 0)
  8.                 continue;
  9.             maxNum = max(maxNum, num);
  10.             minNum = min(minNum, num);
  11.             if (us.count(num)) return false;
  12.             us.insert(num);
  13.         }
  14.         return maxNum - minNum < 5; // 最大数减去最小数是否小于五
  15.     }
  16. };

剑指 Offer 40. 最小的k个数

image.png

  1. class Solution {
  2. public:
  3.     vector<int> getLeastNumbers(vector<int>& arr, int k) {
  4.         sort(arr.begin(), arr.end());
  5.         vector<int> res;
  6.         for (int i = 0; i < k; i++) {
  7.             res.push_back(arr[i]);
  8.         }
  9.         return res;
  10.     }
  11. };

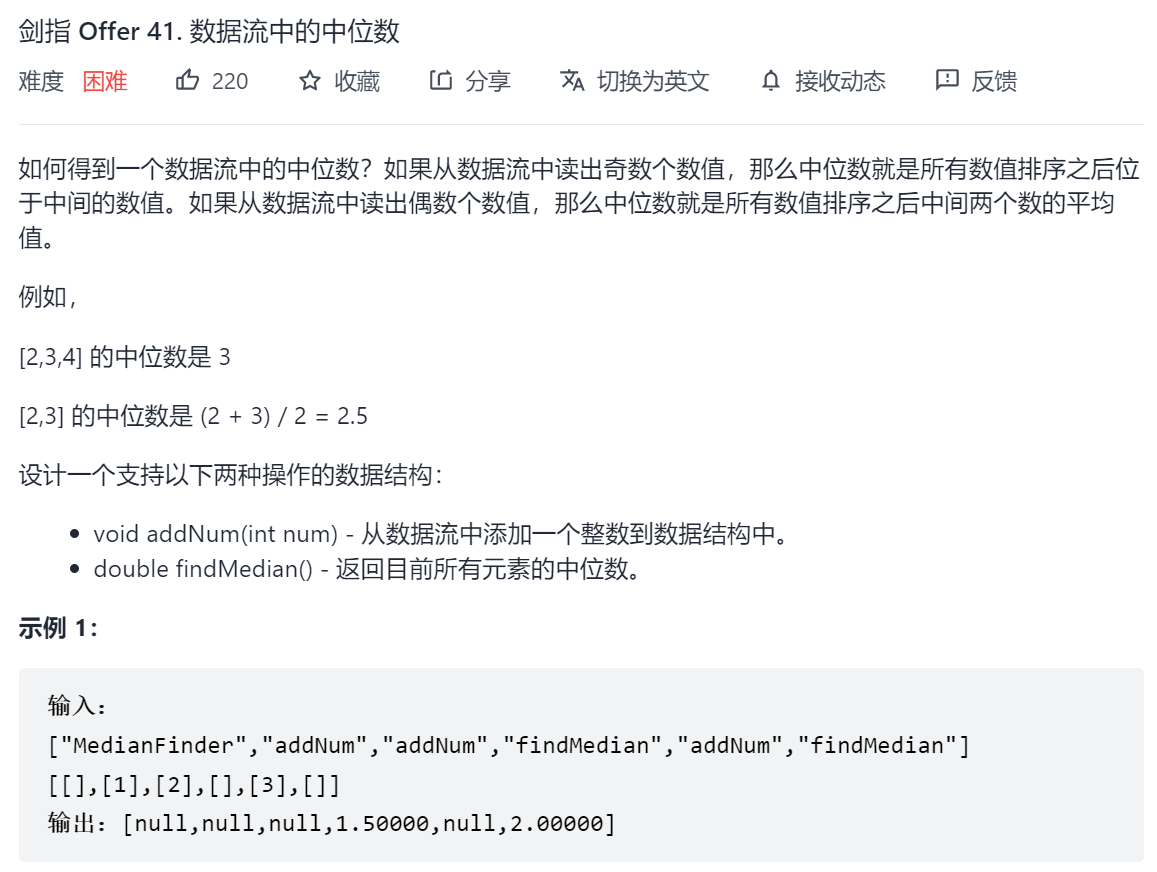
剑指 Offer 41. 数据流中的中位数

image.png
image.png

  1. class MedianFinder {
  2. public:
  3.     priority_queue<int, vector<int>, less<int>> queMin;
  4.     priority_queue<int, vector<int>, greater<int>> queMax;
  6.     MedianFinder() {}
  8.     void addNum(int num) {
  9.         if (queMin.empty() || num <= queMin.top()) {
  10.             queMin.push(num);
  11.             if (queMax.size() + 1 < queMin.size()) {
  12.                 queMax.push(queMin.top());
  13.                 queMin.pop();
  14.             }
  15.         } else {
  16.             queMax.push(num);
  17.             if (queMax.size() > queMin.size()) {
  18.                 queMin.push(queMax.top());
  19.                 queMax.pop();
  20.             }
  21.         }
  22.     }
  24.     double findMedian() {
  25.         if (queMin.size() > queMax.size()) {
  26.             return queMin.top();
  27.         }
  28.         return (queMin.top() + queMax.top()) / 2.0;
  29.     }
  30. };
  32. /**
  33.  * Your MedianFinder object will be instantiated and called as such:
  34.  * MedianFinder* obj = new MedianFinder();
  35.  * obj->addNum(num);
  36.  * double param_2 = obj->findMedian();
  37.  */