134. 加油站💦
暴力解法
遍历整个数组,看从i出发,是否能够回到i
class Solution {public:int canCompleteCircuit(vector<int>& gas, vector<int>& cost) {int n = gas.size();int curGas; // 当前油量for (int i = 0; i < n; i++) {curGas = gas[i];int j = i;while (curGas - cost[j] >= 0) { // 油量足以走到下一个加油站curGas -= cost[j];j = (j + 1) % n; // 走到下一个加油站curGas += gas[j]; // 加油if (j == i) return i;}}return -1;}};
模拟解法
直接从全局进行贪心选择,情况如下:
- 情况一:如果gas的总和小于cost总和,那么无论从哪里出发,一定是跑不了一圈的
- 情况二:rest[i] = gas[i]-cost[i]为一天剩下的油,i从0开始计算累加到最后一站,如果累加没有出现负数,说明从0出发,油就没有断过,那么0就是起点。
- 情况三:如果累加的最小值是负数,汽车就要从非0节点出发,从后向前,看哪个节点能这个负数填平,能把这个负数填平的节点就是出发节点。
class Solution {public:int canCompleteCircuit(vector<int>& gas, vector<int>& cost) {int n = gas.size();int minGasSum = INT_MAX;int curSum = 0;for (int i = 0; i < n; i++) {int rest = gas[i] - cost[i];curSum += rest;minGasSum = min(curSum, minGasSum);}if (curSum < 0) return -1;if (minGasSum >= 0) return 0;for (int i = n - 1; i > 0; i--) {int rest = gas[i] - cost[i];minGasSum += rest;if (minGasSum >= 0)return i;}return -1;}};
贪心
可以换一个思路,首先如果总油量减去总消耗大于等于零那么一定可以跑完一圈,说明 各个站点的加油站 剩油量rest[i]相加一定是大于等于零的。
每个加油站的剩余量rest[i]为gas[i] - cost[i]。
i从0开始累加rest[i],和记为curSum,一旦curSum小于零,说明[0, i]区间都不能作为起始位置,起始位置从i+1算起,再从0计算curSum。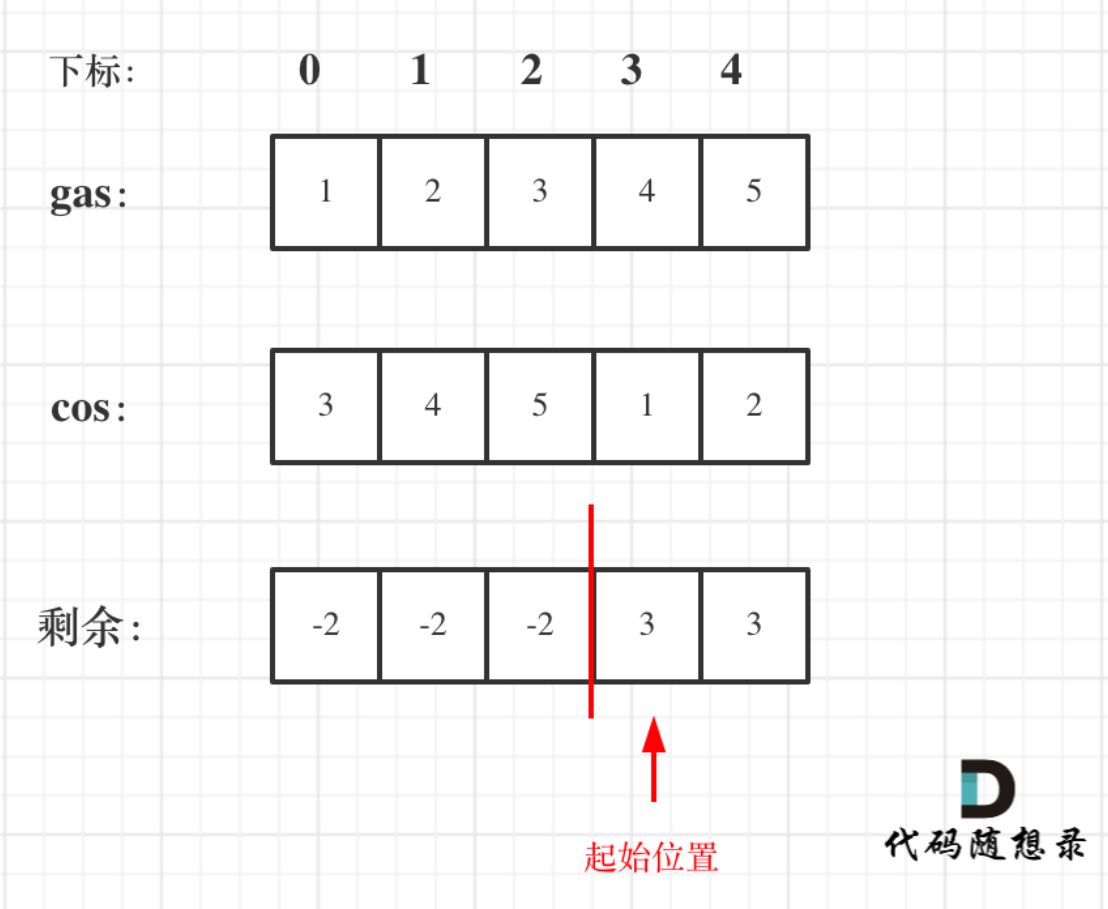
那么为什么一旦[i,j] 区间和为负数,起始位置就可以是j+1呢,j+1后面就不会出现更大的负数?
如果出现更大的负数,就是更新j,那么起始位置又变成新的j+1了。
而且j之前出现了多少负数,j后面就会出现多少正数,因为耗油总和是大于零的(前提我们已经确定了一定可以跑完全程)。
那么局部最优:当前累加rest[j]的和curSum一旦小于0,起始位置至少要是j+1,因为从j开始一定不行。全局最优:找到可以跑一圈的起始位置。
note:
[i, j]为rest和为负数的话,因为区间的前几个数必然是正的(不是正的无法作为起点),后面的都是负的,才导致rest和小于零,减少正数(起点更新至i后面的位置)只会使rest和更小,而取rest为负的作为起点更是不行,所以[i, j]区间内任何一个点都不能是起点(到不了j就没油了),要从j+1开始重新判断
class Solution {public:int canCompleteCircuit(vector<int>& gas, vector<int>& cost) {int n = gas.size();int start = 0, curSum = 0, totalSum = 0;for (int i = 0; i < n; i++) {int rest = gas[i] - cost[i];curSum += rest;totalSum += rest;if (curSum < 0) {curSum = 0;start = i + 1;}}if (totalSum < 0) return -1;return start;}};
- 时间复杂度:O(n)
- 空间复杂度:O(1)
贪心证明(力扣官方题解)

找到第一个无法到达的加油站,通过证明从出发位置到当前加油站中的任意加油站都不能达到第一个加油站的后一个位置,那么可以从后一个位置开始重新搜索class Solution {public:int canCompleteCircuit(vector<int>& gas, vector<int>& cost) {int n = gas.size();int i = 0; // 初始从第一个加油站开始搜索while (i < n) {int sumGas = 0, sumCost = 0, cnt = 0; // cnt 表示从i出发能够走多远while (cnt < n) {int j = (i + cnt) % n;sumCost += cost[j];sumGas += gas[j];if (sumCost > sumGas) break; // 找到从i出发第一个不能到到的加油站cnt++;}if (n == cnt) return i; // 从i出发可以绕一周else i = i + cnt + 1;}return -1;}};
781. 森林中的兔子
思路一:数学
当某种颜色的兔子回答 x 时,最多有x+1个兔子有这种颜色(说话的兔子和它看到的其他同颜色兔子之和)
如果有13只兔子回答5,随便抓一只回答5的兔子,假设兔子是白的,那么同样白色的兔子还有5只,白色的兔子一共6只。再抓一只说5的灰色兔子,灰色兔子一共也有六只,要求兔子的最小数量,因此假设灰色和白色共12只都在这13只中,那么还有一只兔子是其他颜色的,也就是说13只兔子回答5这种情况下,最少有18只兔子。
假设有x只兔子回答y,那么最少需要的兔子颜色有种,每种颜色的数量为
因此最少的兔子数为:
贪心策略,尽可能让说一个数字的兔子属于同一种颜色
class Solution {public:int numRabbits(vector<int> &answers) {// 创建无序集合,为了统计说 y 的兔子共有几只// key: y// value: xunordered_map<int, int> count;for (int y : answers) {++count[y];}int ans = 0;//for (auto &[y, x] : count) {// 直接从集合中取出[key: value] 是C++17的新特性//ans += (x + y) / (y + 1) * (y + 1);//}for(auto p: count) {int x = p.second;int y = p.first;ans += (x + y)/(y + 1) * (y + 1);// 分子 +y 是为了实现向上取整}return ans;}}
思路二:分组
class Solution {public:int numRabbits(vector<int>& answers) {// 如果有x个兔子喊y,那么最多有y+1个兔子是同一种颜色的,其他的必然是不同颜色unordered_map<int, int> count; // first:喊n颜色且为color second:喊n的兔子并且颜色为color的兔子最多还能有几只int res = 0;for (int i = 0; i < answers.size(); i++) {if (count[answers[i]] == 0) { // 新建一种颜色,假设为红色res += answers[i] + 1; // 累加兔子数量count[answers[i]] = answers[i]; // 表示最多还有answers[i]只红兔子可以喊这个数} else {count[answers[i]]--; // 可以喊answers[i]的红兔子减少一只}}return res;}};
860. 柠檬水找零
思路
用一个哈希表(或者两个变量)记录已有的零钱数,20不用记,因为不会用20来找零
贪心策略,顾客给你20块,优先找他十块的,才能保证尽可能多的顾客都能被找零
class Solution {
public:
bool lemonadeChange(vector<int>& bills) {
unordered_map<int, int> um; // 记录你手头的零钱
for (int i = 0; i < bills.size(); i++) {
if (bills[i] == 5) {
um[5]++; // 不用找零
} else if (bills[i] == 10) {
if (um[5] > 0) {
um[10]++;
um[5]--; // 找五元
} else return false; // 找不开,返回false
} else if (bills[i] == 20) {
if (um[10] > 0 && um[5] > 0) {
um[10]--;
um[5]--;
} else if (um[5] > 3) {
um[5] -= 3;
} else return false;
}
}
return true;
}
};
精简写法:
class Solution {
public:
bool lemonadeChange(vector<int>& bills) {
int five = 0, ten = 0;
for (int i : bills) {
if (i == 5) five++;
else if (i == 10) {five--; ten++;}
else if (ten > 0) {ten--; five--;}
else five -= 3;
if (five < 0) return false;
}
return true;
}
};
406. 根据身高重建队列

像这种两个维度的题,比如分发糖果,一定是先确定一个维度,再去考虑如何确定另外一个维度
那么用示例一来举例,分析一下
输入:people = [[7,0],[4,4],[7,1],[5,0],[6,1],[5,2]] 输出:[[5,0],[7,0],[5,2],[6,1],[4,4],[7,1]] 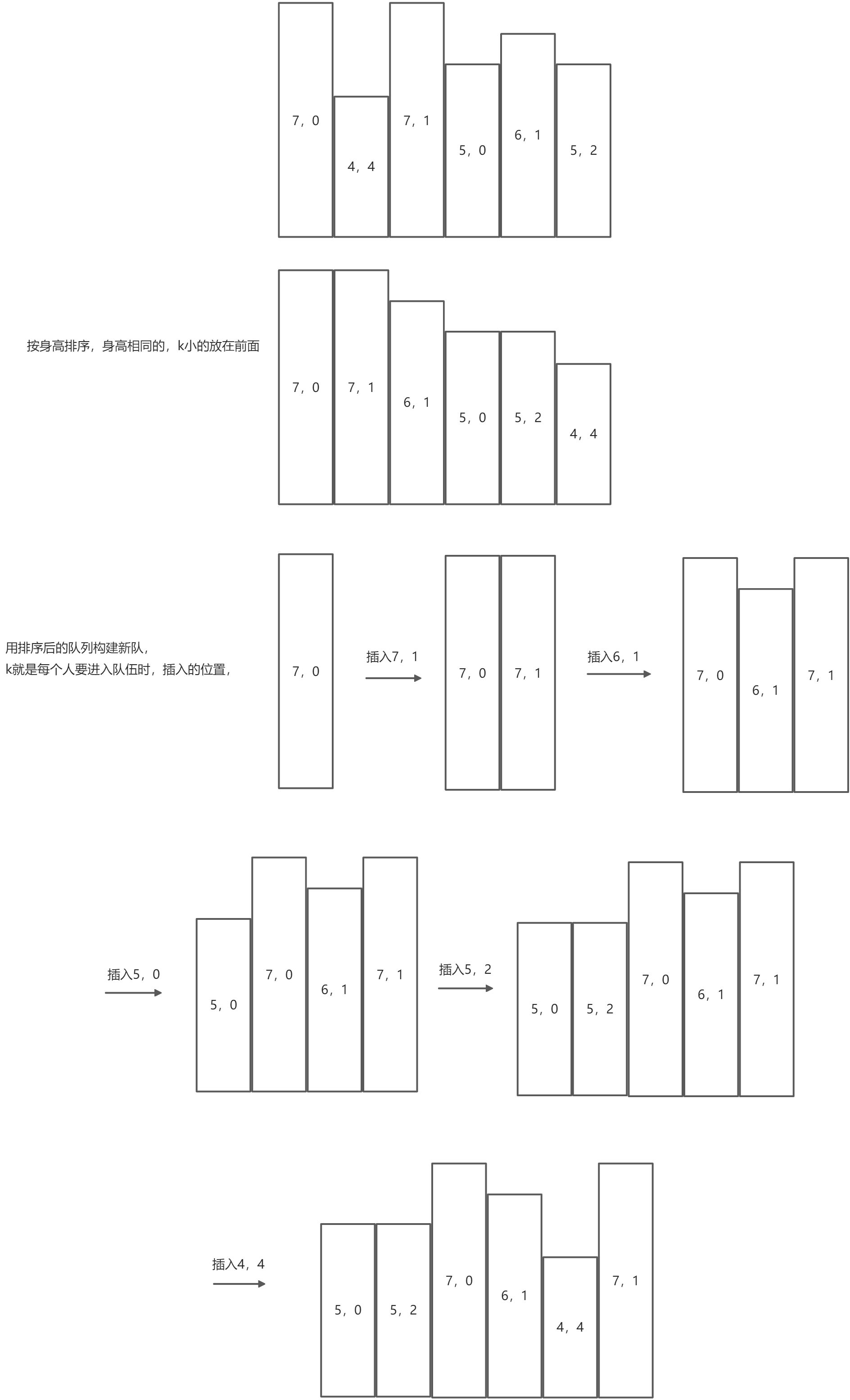
先按照身高降序,ki升序,然后按照排序后的数组逐个向res中插入,插入一个人时,只有两种情况:
- 队伍里的人都比他高,那么将其插入队伍的最开始
队伍里有ki个人身高等于他,由于身高相同的人按照ki降序,所以将其插入队伍的第ki个位置
class Solution { public: vector<vector<int>> reconstructQueue(vector<vector<int>>& people) { sort(people.begin(), people.end(), [](auto& p1, auto& p2) { if (p1[0] == p2[0]) return p1[1] < p2[1]; // 身高相同的按ki升序 return p1[0] > p2[0]; // 按身高降序 }); vector<vector<int>> res; for (auto& p : people) { res.insert(res.begin() + p[1], p); } return res; } };顺序表插入操作比较费时,可以链表来降低时间复杂度
class Solution { public: vector<vector<int>> reconstructQueue(vector<vector<int>>& people) { // 先按身高从高到低排序,身高一样的k小的站在前面 sort(people.begin(), people.end(), [](vector<int>& v1, vector<int>& v2)->bool{ if (v1[0] == v2[0]) return v1[1] < v2[1]; return v1[0] > v2[0]; }); list<vector<int>> que; // 遍历已经排序好的队伍,然后处理ki维,根据前面有多少比他高的选择合适的插入位置 for (int i = 0; i < people.size(); i++) { // 身高排序后,前面比他高的人的个数hi就是他要插入的位置 int loc = people[i][1]; std::list<vector<int>>::iterator it = que.begin(); // 寻找插入位置 while(loc--) it++; que.insert(it, people[i]); } return vector<vector<int>>(que.begin(), que.end()); } };时间复杂度O(nlogn + n^2)总体O(N)
- 空间复杂度O(logN)排序用栈
注:C++中vector(可以理解是一个动态数组,底层是普通数组实现的)如果插入元素大于预先普通数组大小,vector底部会有一个扩容的操作,即申请两倍于原先普通数组的大小,然后把数据拷贝到另一个更大的数组上。
所以使用vector(动态数组)来insert,是费时的,插入再拷贝的话,单纯一个插入的操作就是O(n^2)了,甚至可能拷贝好几次,就不止O(n^2)了。
738. 单调递增的数字
思路一:贪心
从后向前遍历数字,如果出现前一个数字大于后一个数字的情况,那么令前一个数字减一,并将后一个数字赋值为9,前一位减一可以保证这个数字不会超过原来的数,这样可以保证这两位编程最大单调递增的整数(局部最优),从后向前调整还能够保证不会改变之前调整的结果,这样最后就达到全局最优
需要用一个标记,记录从哪一位开始变成9,最后统一变换
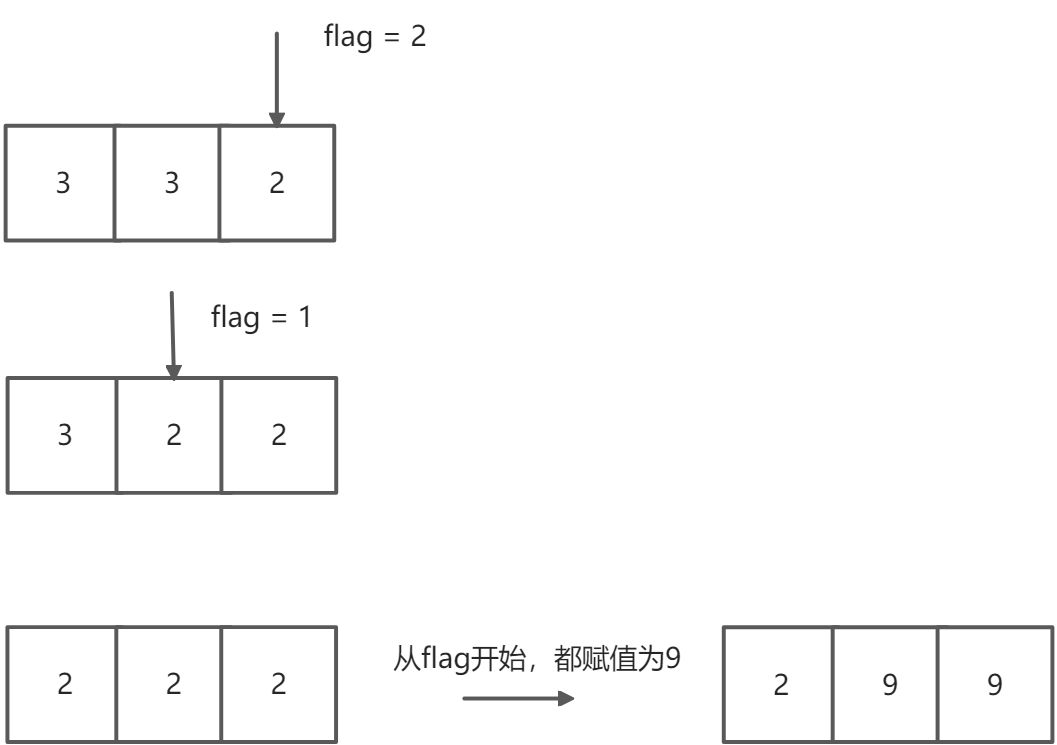
如果不用标记为,在比较数字大小变换时,会发生这种情况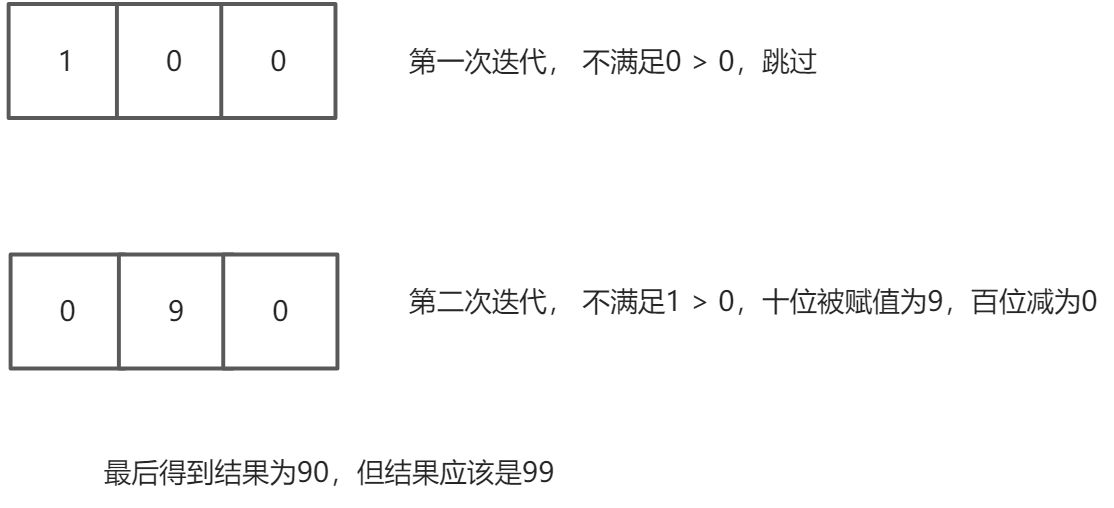
事实上,只要个位前面的任意一位减一了,那么都应该让那一位右边的所有位都置为9,才能保证得到的数字是最大的。
class Solution {
public:
int monotoneIncreasingDigits(int n) {
if(n < 10) return n;
string s = to_string(n);
int len = s.size();
int flag = len; // 标记从哪一位开始变为9
for (int i = len - 1; i > 0; i--) {
if (s[i - 1] > s[i]) {
s[i - 1]--;
flag = i;
}
}
for (int i = flag; i < len; i++) s[i] = '9';
return stoi(s);
}
};
- 时间复杂度:O(n) n 为数字长度
空间复杂度:O(n) 需要一个字符串,转化为字符串操作更方便
思路二
在评论区发现一个非常巧妙的写法
直接通过除法和取余获得每次比较的两位,如果前一位大于后一位,直接通过整除将后面数置零,然后减一,实现了前一位减一,后面所有数字置为9的操作。
举个例子:
332 ,因为3>2,所以332整除10再乘以10得到320,330-1得到329
然后取32,因为3>2,所以329整除100再乘以100得到300,300-1得到299class Solution { public: int monotoneIncreasingDigits(int n) { int res = n; int i = 1; while (i <= res) { n = res / i % 100; // 取后两位 i *= 10; if (n / 10 > n % 10) res = res / i * i - 1; // 这个操作实现了前一位减一后面所有数置为9 } return res; } };时间复杂度:O(n) n 为数字长度
- 空间复杂度:O(1)
968. 监控二叉树
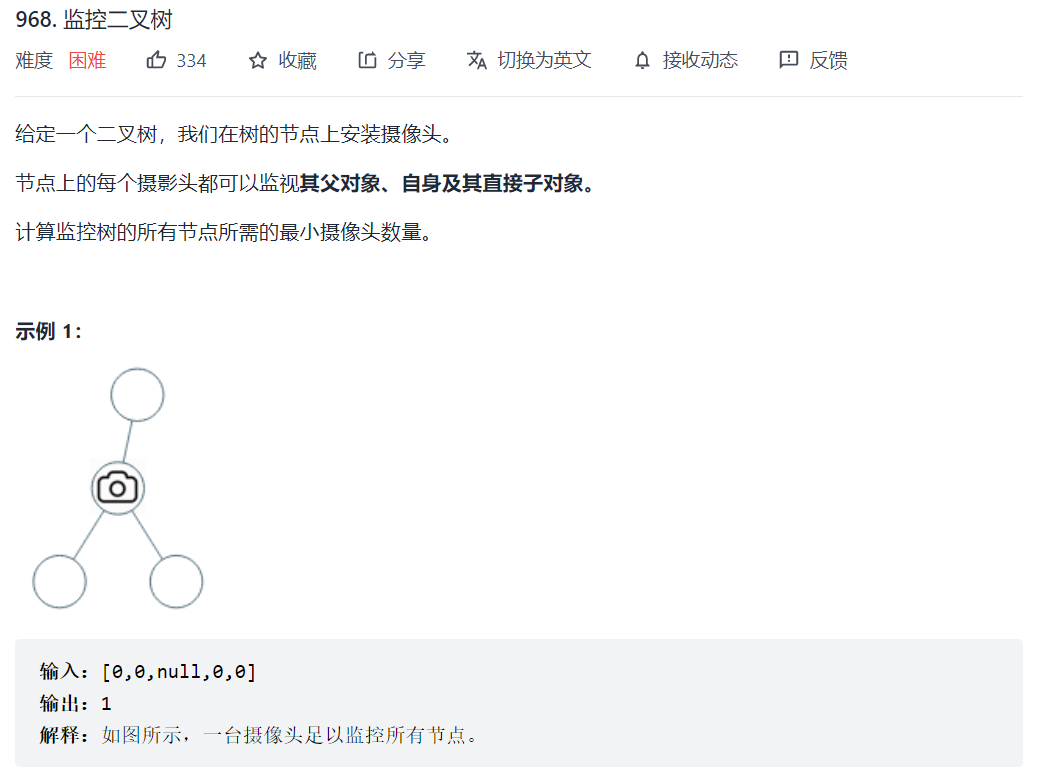
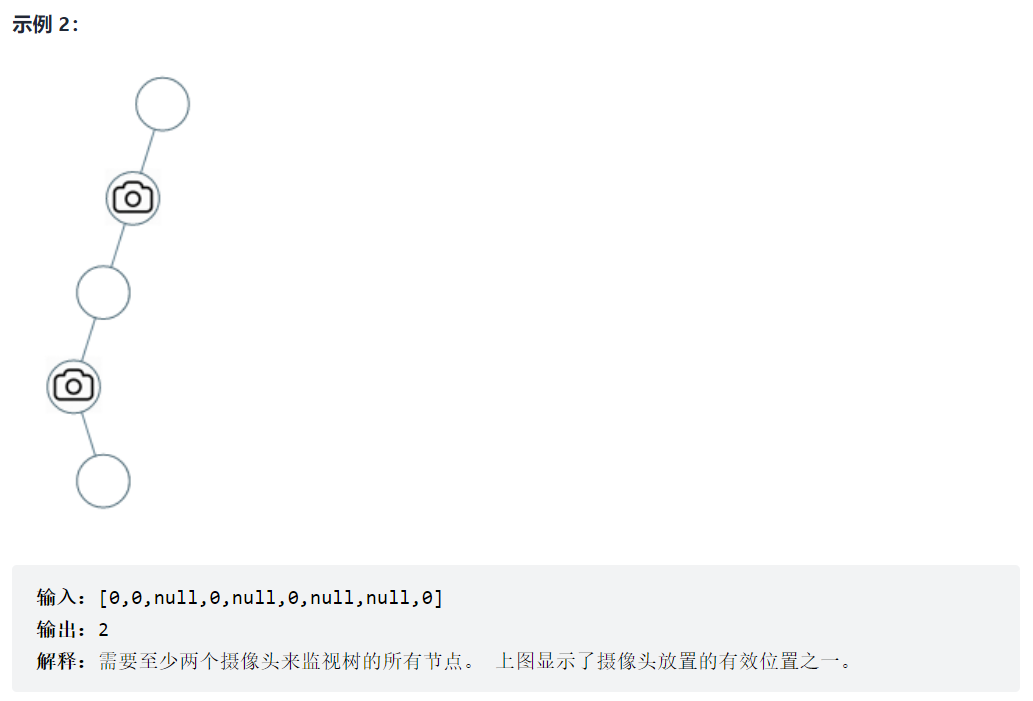
如何放置,才能让摄像头最小的
从题目中示例,其实可以得到启发,发现题目示例中的摄像头都没有放在叶子节点上!
这是很重要的一个线索,摄像头可以覆盖上中下三层,如果把摄像头放在叶子节点上,就浪费的一层的覆盖。
所以把摄像头放在叶子节点的父节点位置,才能充分利用摄像头的覆盖面积。
所以我们要从下往上看,局部最优:让叶子节点的父节点安摄像头,所用摄像头最少,整体最优:全部摄像头数量所用最少
局部最优推出全局最优,找不出反例,那么就按照贪心来!
此时,大体思路就是从低到上,先给叶子节点父节点放个摄像头,然后隔两个节点放一个摄像头,直至到二叉树头结点。
此时这道题目还有两个难点:
- 二叉树的遍历
- 如何隔两个节点放一个摄像头
从下到上遍历,采用后序遍历
状态转移的公式:
每个节点可能有的几种状态:
- 该节点无覆盖,无摄像头0
- 本节点有摄像头 1
- 本节点有覆盖,无摄像头2
空节点的状态:空节点的状态只能是有覆盖,空节点的父节点是叶子节点,为了使安装的摄像头尽可能少,不应该在叶子结点上安装摄像头,那么要保证推导的时候所有节点(包括空节点)都是覆盖状态,那么只能将空节点设置为是覆盖状态
所以递归的终止条件:
// 空节点,该节点有覆盖
if (cur == NULL) return 2;
单层逻辑:
- 情况1:左右节点都有覆盖且无摄像头。后序遍历,左右节点都是被覆盖状态,那么当前节点处于无覆盖状态,返回0
- 情况2:左右节点至少有一个无覆盖的情况。左右孩子有未被覆盖的,必须在当前节点安装摄像头,返回1,并将摄像头数量加一
- left == 0 && right == 0
- left == 1 && right == 0
- left == 0 && right == 1
- left == 0 && right == 2
- left == 2 && right == 0
- 将上述合成一个条件:left == 0 || right == 0
- 情况3:左右节点至少有一个有摄像头,left == 1 || right == 1,父节点处于被覆盖状态,返回2
- 情况4:头结点没有覆盖,后序遍历完了之后,根结点如果还没被覆盖,在根结点再放置一个摄像头
代码:
class Solution {
public:
int res;
int dfs(TreeNode* node) {
if (node == nullptr) return 2; // 空节点处于被覆盖状态
int left = dfs(node->left);
int right = dfs(node->right);
if (left == 2 && right == 2) return 0; // 左右孩子都有覆盖,返回0
if (left == 0 || right == 0) { // 左右孩子有未被覆盖的,在此安装一个摄像头
res++;
return 1;
}
if (left == 1 || right == 1) return 2; // 左右孩子有摄像头,此节点被覆盖
return 2; // 力扣编译器要求必须有返回值,实际不会执行这一句
}
int minCameraCover(TreeNode* root) {
res = 0;
if (dfs(root) == 0) res++;
return res;
}
};
也可以 if - else if
class Solution {
public:
int res;
int dfs(TreeNode* node) {
if (node == nullptr) return 2; // 空节点处于被覆盖状态
int left = dfs(node->left);
int right = dfs(node->right);
if (left == 2 && right == 2)
return 0; // 左右孩子都有覆盖,返回0
else if (left == 0 || right == 0) { // 左右孩子有未被覆盖的,在此安装一个摄像头
res++;
return 1;
} else
return 2; // 左右孩子有摄像头,此节点被覆盖
}
int minCameraCover(TreeNode* root) {
res = 0;
if (dfs(root) == 0) res++;
return res;
}
};