神经网络在测试集上表现不好，很可能不是过拟合的问题，往往是在训练集上就表现的不好。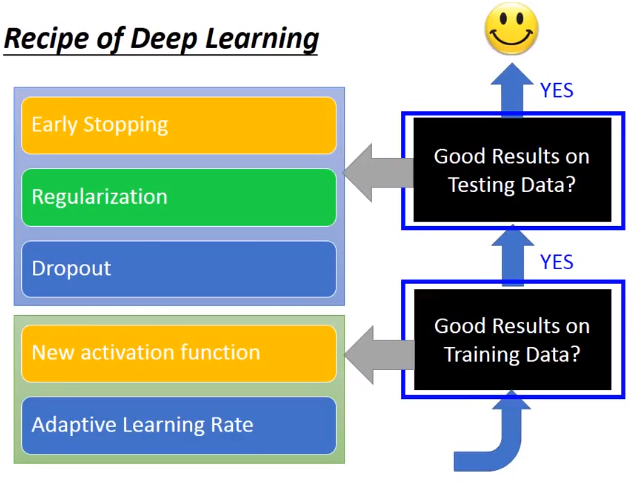
image.png

1.提升训练集上的表现

1.1更换激活函数

sigmoid函数：梯度消失问题

如果激活函数是sigmoid，根据函数特性，对于输入较大的变化，输出把这种变化缩小了。层层缩小，到最后，输入（Input）的变化对最终输出（Output）的影响非常小，即梯度不再有变化。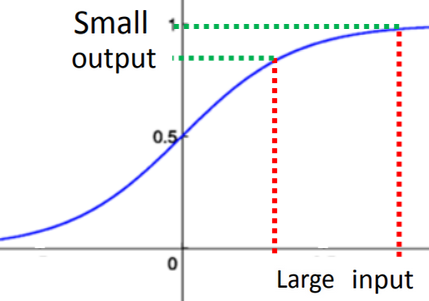
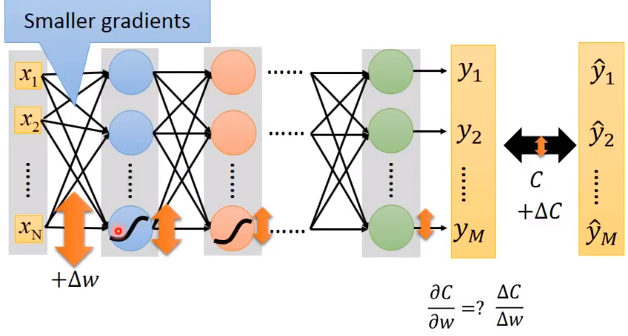
image.png image.png

tanh：梯度消失问题

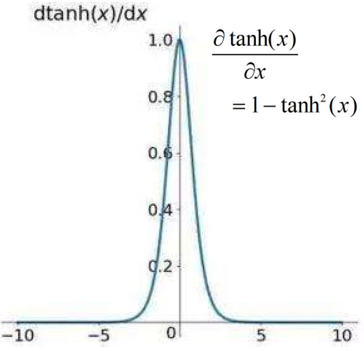
tanh函数曲线关于原点对称，将输出压缩到（-1,1）的范围；但也存在梯度消失（梯度饱和）问题，而且计算形式更复杂了。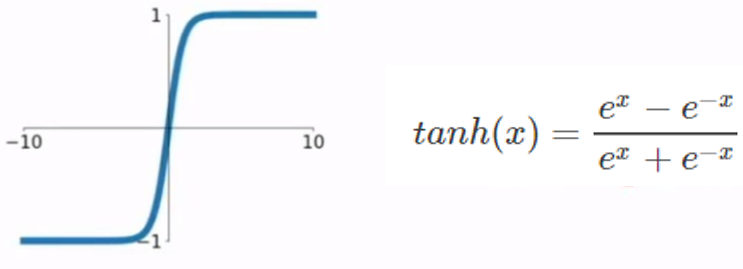
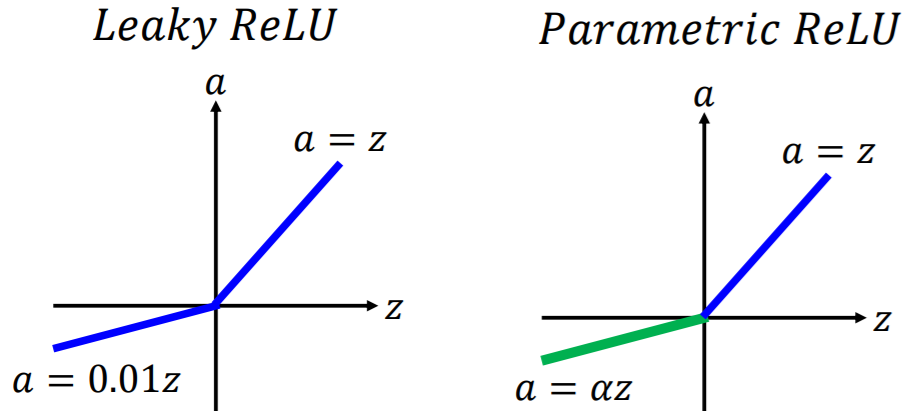
image.png image.png

ReLu

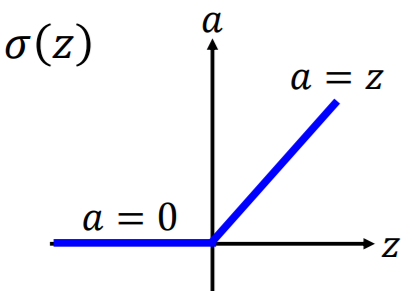
image.png
a=0时，相当于神经元死亡；多层线性相乘，等价于1层。
选择ReLU整流线性单元（Rectified Linear Unit）作为激活函数的优势在于：

  • 函数简单，易于计算。
  • 符合生物神经元特性。（即神经元不是一受刺激就有反应，而是累积一段时长，才有输出）
  • ReLU可以由无数个sigmoid叠加而成
  • ReLU可以解决梯度消失问题。（因为当输入大于0时，输入等于输出，不会层层衰减。）

ReLU的变种：
image.png

Maxout：自动学习的激活函数

  • Maxout工作原理：分组取最大值

神经元中的激活函数是一个取最大值的函数：将每层的输出分若干组，每组有若干个输出，每组中取各自最大的值作为神经元的输出。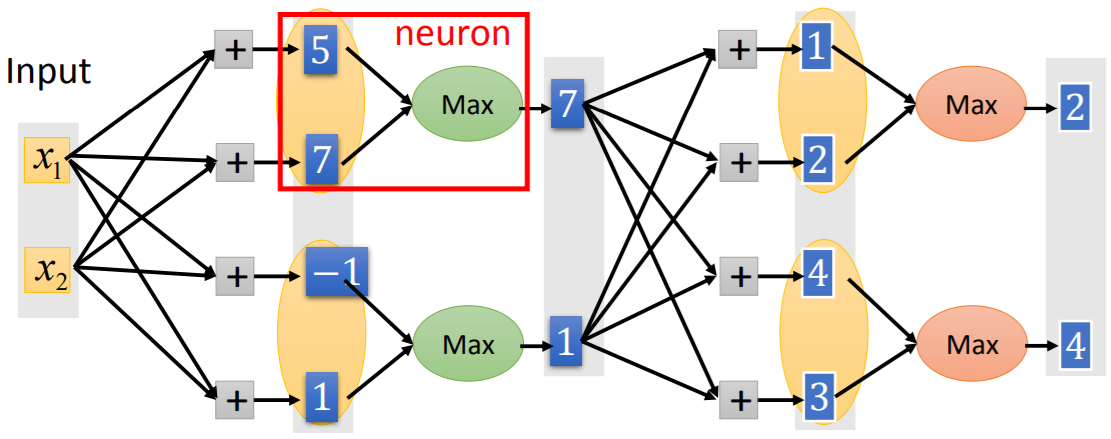
image.png

  • ReLU是Maxout的一个特例。

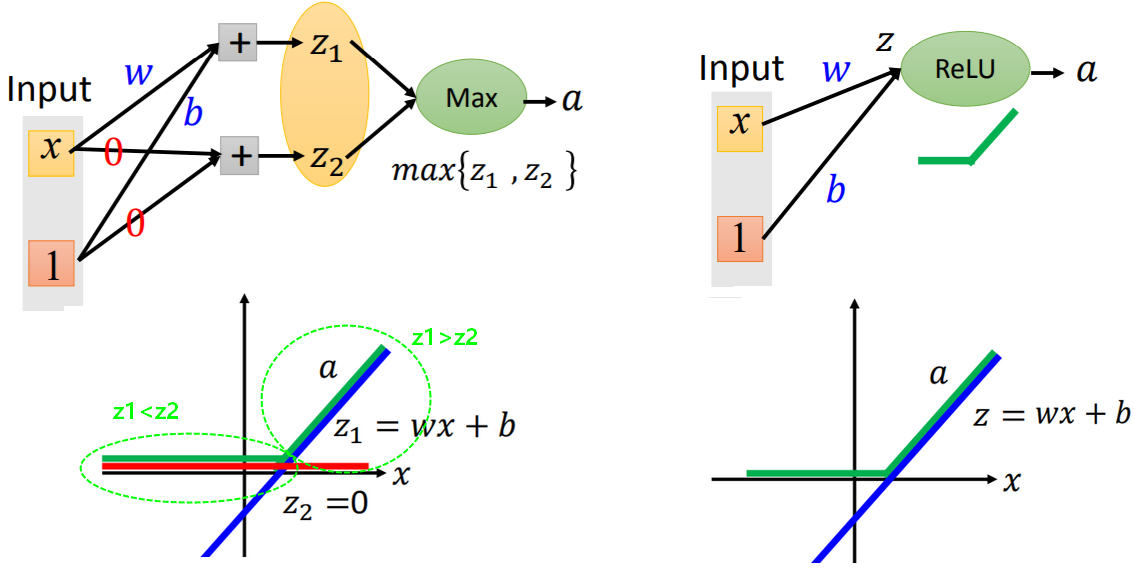
image.png

  • Maxout可以呈现出任何分段的（piecewise）线性凸函数（convex）。

Maxout呈现出的分段函数形状和特征上的参数有关，在学习时，可以根据参数的不同，画出的函数形状也不同，即可以自动学习激活函数。分段函数有多少段，由每组中元素的个数决定。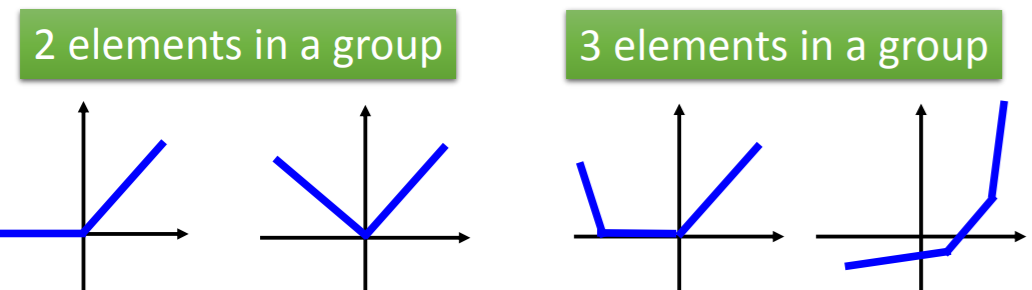
image.png
【问题】如何训练以Maxout作为激活函数的神经网络？
表面上看，分组取最大值后，神经网络变得瘦长：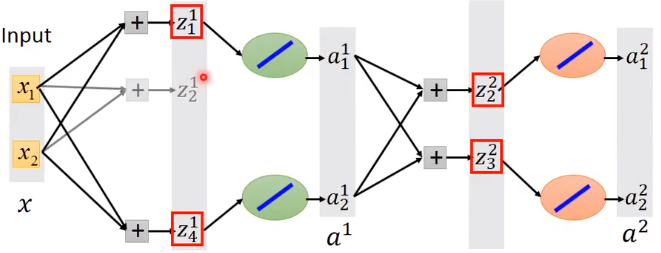
image.png
但实际，每次的输入是不同的，每次分组取最大值后Maxout的输出也不同，所以正常进行反向传播，每层的参数都会被更新。

1.2自适应学习率

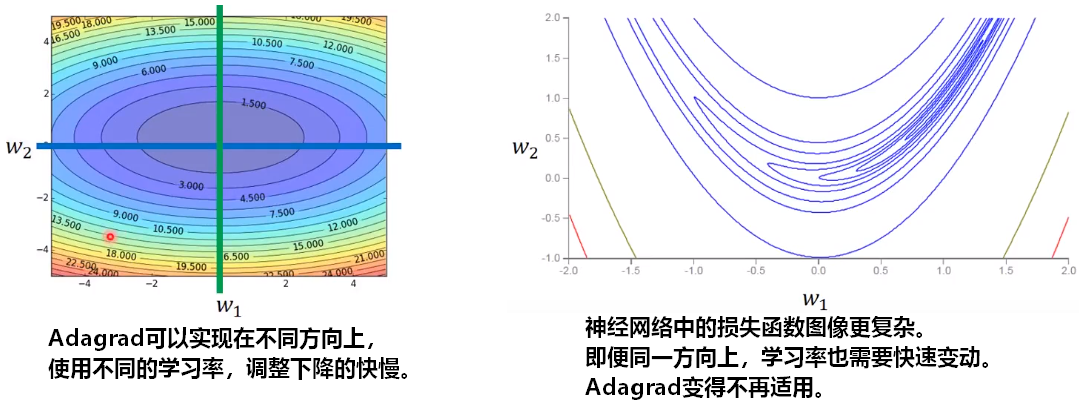
image.png
【问题】如何更动态的更新学习率/步长，更好的在神经网络中进行梯度下降？

RMSProp：Root Mean Square

image.png
【问题】神经网络中，梯度下降，如何避免取到局部最优解？
经研究，神经网络中的损失函数是比较平滑的，一般得到的最优解就是全局最优解，或者非常接近全局最优解。
另外，用于解决局部最优解的方法是，加入物理学中的“惯性”概念。

Momentum：动量

原本梯度下降是走梯度向量的反方向（详见梯度的理论推导），为了尽量避免走入局部最优解，在每一次下降过程中，考虑上一次下降方向对本次下降的影响（即“惯性”）。
image.png
每一次梯度下降的方向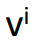image.png，实际上是之前所有梯度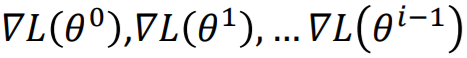image.png的加和，受之前所有梯度的影响。可以看出，受最近的梯度影响较大。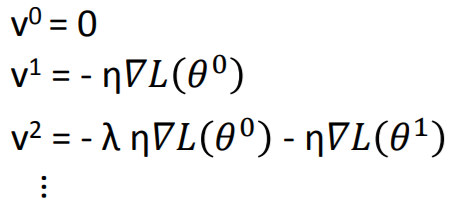
image.png
【注意】加入动量（Momentum）并不一定保证可以找到全局最优解，只是为找到全局最优解提供了更多可能。

Adam：RMSProp+Momentum

image.png

2.提升测试集上的表现

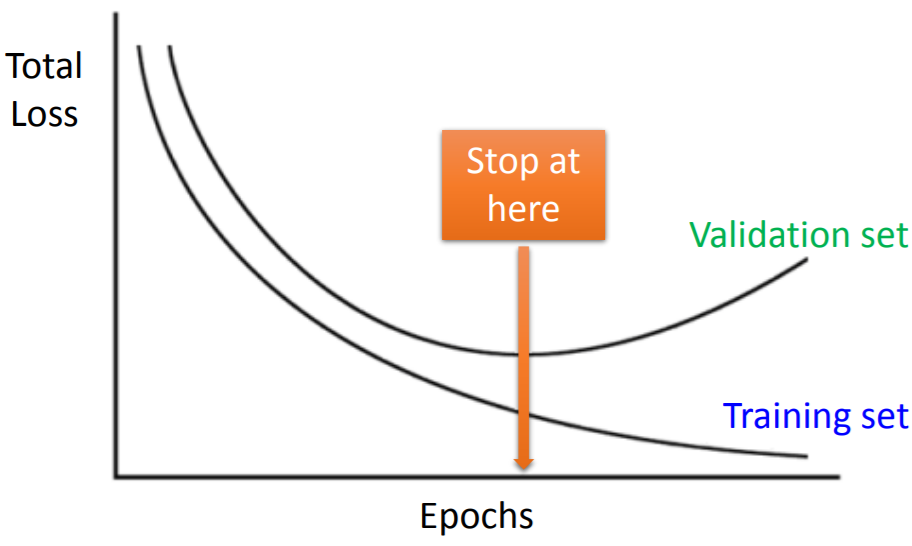
2.1早停法(Early stopping)

使用验证集来及时停止训练轮次，防止训练模型时的过拟合问题。
image.png

2.2正则化

L1正则、L2正则（具体查看“模型的泛化能力”一篇）
在损失函数中加入正则项：

  • L1正则的效果：使参数W向量变得稀疏，元素w的数值差异较大，会牺牲一些较不重要的维度（对应的w为0）。

  • L2正则的效果：使W向量各元素整体上平均的变小。

    2.3Dropout

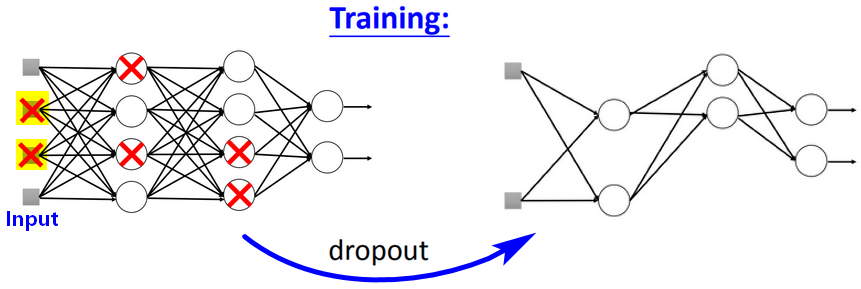
    image.png
    使用Dropout之后，模型在训练集上的效果变差，但模型的泛化能力更强。

    如何做Dropout？

  • 【做法】输入层也要做dropout，dropout就是神经元被随机丢弃掉，即对神经元采样并丢弃。

假设每个神经元都有 p% 的概率被丢弃掉。

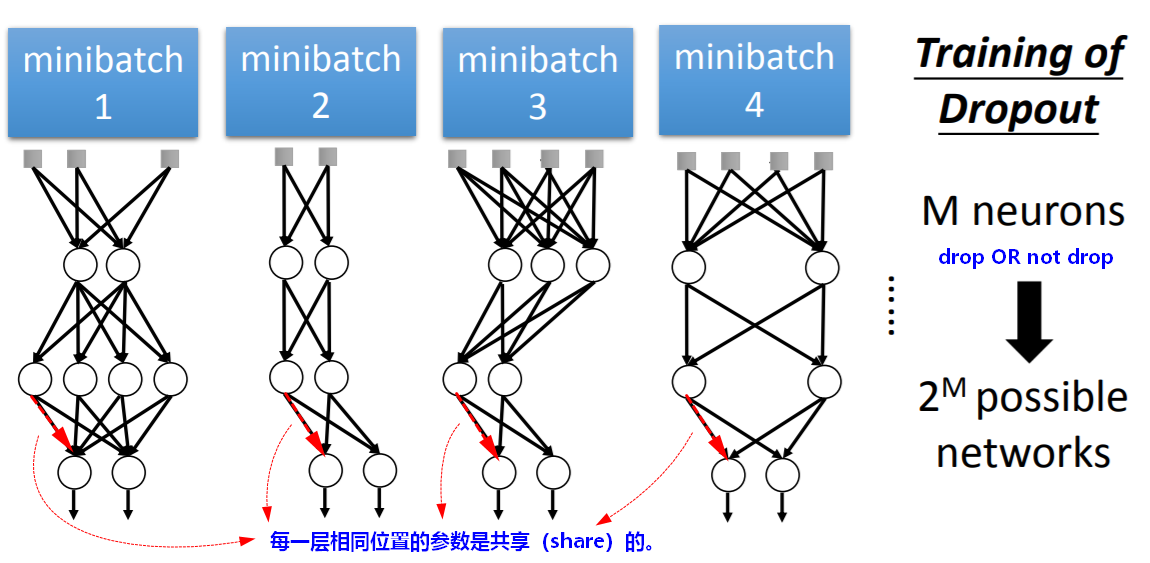
  • 【时机】在每次更新参数前（例如：每次mini-batch时），进行dropout；然后使用新的“瘦身”后的网络进行训练（所以每一次min-batch使用的网络结构都不一样，但在可能的网络模型中，相同神经元连接位置的参数是共享的）。
  • 【测试】测试时，神经网络不进行dropout，但是所有参数都要乘以(1-p%)倍。

【问题】为什么经过dropout进行训练的网络，在测试时所有参数需要乘以(1-p%)？
原因1：假设测试时，使用训练时的参数，输出实际会被放大若干倍，只有参数缩小，才可以获得和训练时近似的输出。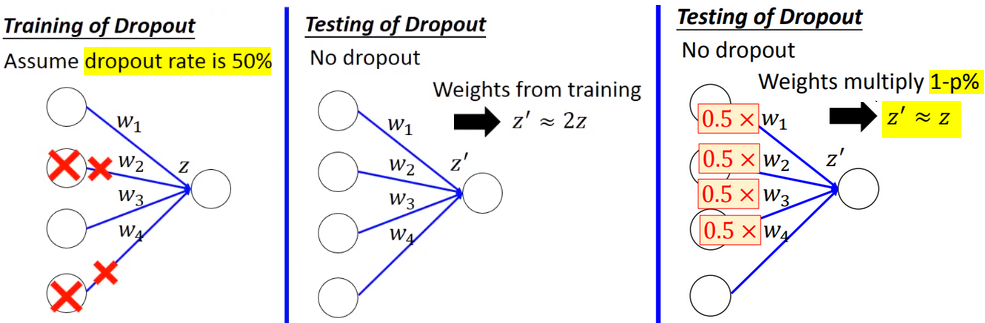
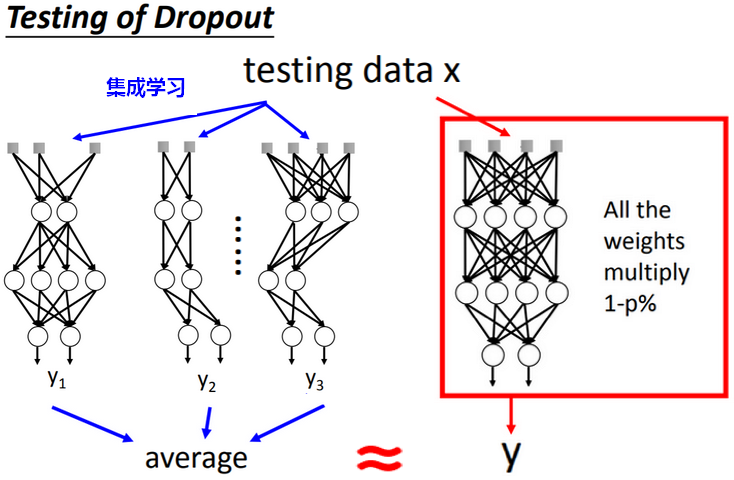
image.png
原因2：使用dropout时，每次mini-batch都得到一个网络模型，dropout实际相当于是集成学习（ensemble）。测试时，所有参数乘以(1-p%)，此时的网络模型相当于是使用了之前训练的若干个模型做输出。

Dropout与集成学习

  • 使用Dropout技巧进行训练时，相当于每个mini-batch都得到一个网络模型，（如果有 M 个神经元）则最多有 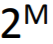image.png 种可能的网络模型。
  • 在可能的网络模型中，相同神经元连接位置的参数是共享的。
  • Dropout技巧是一种集成学习（ensemble）。

  • 但测试时，理论上应该用每个模型（最多共image.png个）做输出并去平均，但模型太多了；此时不使用dropout，但所有参数乘以（1-p%）得到的模型，在效果上是相似的。

    （只有是linear network，ensemble才会等于weights multiply一个值。）
    image.png
    image.png

    Dropout的问题

    牺牲了独立性：理论上，集成学习中（bagging），分类器越独立，集成效果越好；在神经网络（整体有M个神经元）中，dropout之后（丢掉N个神经元），这个分类器就是子神经网络，因为不同的子神经网络之间是共享参数的，这相当于牺牲了独立性；但因为子神经网络有image.png个，通过数量弥补了子神经网络不独立的弊端。
    dropout比例的tradeoff：dropout的概率P越大，子神经网络的独立性越大（因为每个子网络中相同的神经元越少），P=0.5时，子网络数量最多；但是P越大，每个子网络中的神经元数量太少，虽然独立，但学习能力太差。实践中，dropout比例一般设置为0.2~0.3。
    提升泛化能力：因为每个神经元都是一个特征采样，dropout相当于随机忽略特征/减轻特征依赖，可以提升泛化能力。另一角度，dropout某神经元时，相当于连接该神经元的W=0，相当于做了随机的L1正则。

参考： 1.台湾大学李宏毅《机器学习》2017，Spring