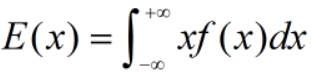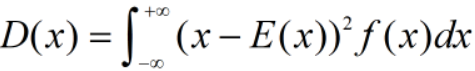1.条件概率
随机事件:有可能发生,也可能不发生的事件。
假设 随机事件a、b是两个相关的事件。
条件概率:在某事件发生的条件下另一事件发生的概率。例如: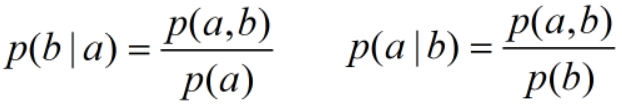
先验概率、后验概率
随机事件独立
- 如果
 ,则称随机事件 a和b独立,即各自发生的概率和另一事件无关。
,则称随机事件 a和b独立,即各自发生的概率和另一事件无关。 当随机事件a和b独立时,a和b同时发生的概率为:
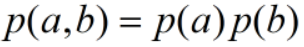
n个相互独立的随机事件同时发生的概率:
2.随机变量
离散型随机变量
定义
离散型随机变量的取值是有限个或者无限可列个(例如:整数集)。
- 变量分布情况:概率分布表
可以使用概率分布表描述离散型随机变量的分布。此时,概率满足: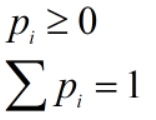
- 常见的概率分布
连续型随机变量
- 定义
连续型随机变量的取值是无限不可列个(例如:实数集)。
- 变量分布情况:概率密度函数
从离散型随机变量的概率分布表推广到无限情况,
连续型随机变量的概率密度函数满足: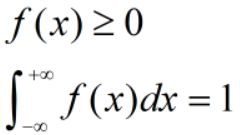
- 概率分布函数 y
连续型随机变量的分布函数y是概率密度函数的变上限积分: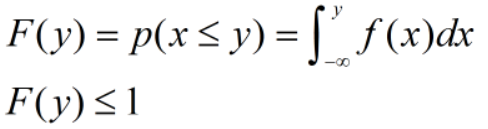 该函数是增函数。
该函数是增函数。
(连续型随机变量取某个值的概率为0,但这个取值落在某一区间的值可以不为0)
- 常见的概率分布
高斯分布
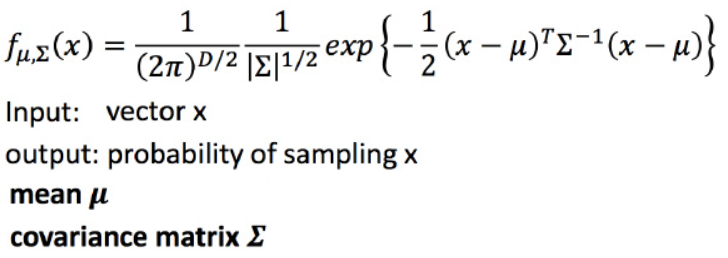
协方差矩阵相同,而均值不同,则概率分布的最高点的位置不同,离散度一样。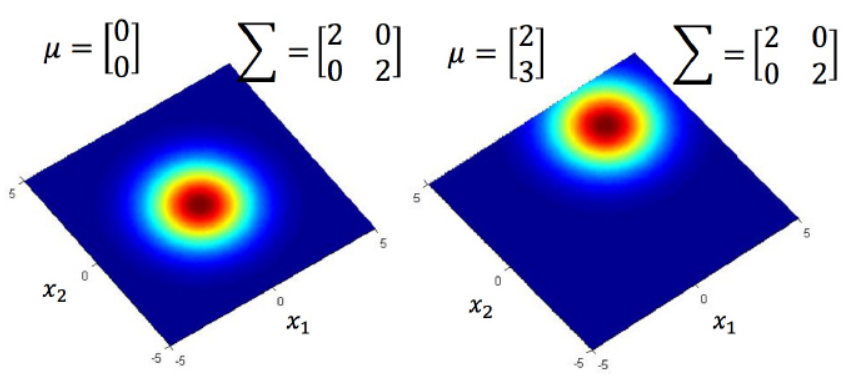
均值相同,而协方差矩阵不同,则概率分布的最高点的位置相同,但离散度不同。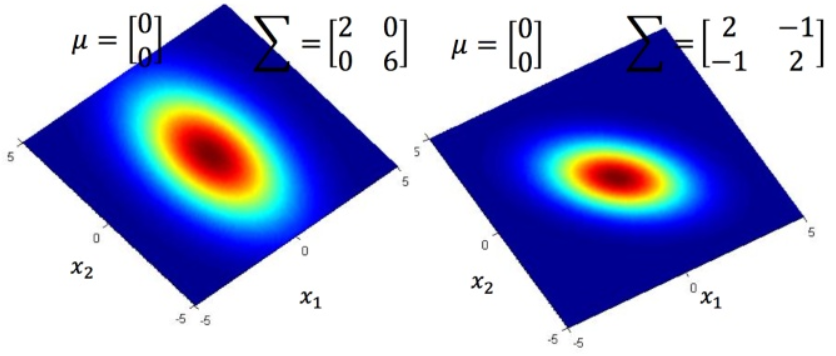
数学期望、方差
数学期望是随机变量在概率意义下的均值,是加权平均值的抽象。
方差反映的是随机变量取值的变化程度,方差越小,取值变化的程度越小。
- 对于离散型随机变量 x
数学期望: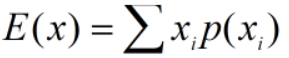
方差: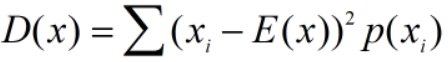
- 对于连续型随机变量 x,假设其概率密度函数是 f(x)
协方差
协方差用于描述两个随机变量之间线性关系的强弱。
协方差定义为: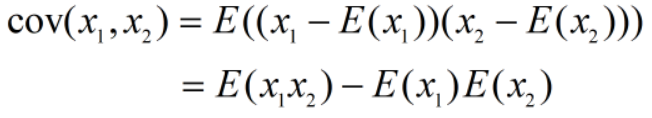
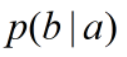 为先验概率。
为先验概率。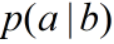 为后验概率。
为后验概率。