DBSCAN聚类

1.DBSCAN：思想和步骤

DBSCAN(Density-Based Spatial Clustering of Applications with Noise)是一种基于密度的聚类算法。它可以在具有噪音的空间数据中发现任意形状的簇（噪音鲁棒，对噪声不敏感）；并将具有足够密度的区域划分为簇，这个簇就是密度相连的点的最大集合（从一个核心点出发，不断向密度可达的区域扩张）。

1.1密度、核心点

数据集中特定点的密度：通过该点Eps半径之内的点计数（包括该点本身）来估计，即该点Eps邻域内的样本数。所以，密度依赖半径。基于密度，有如下概念：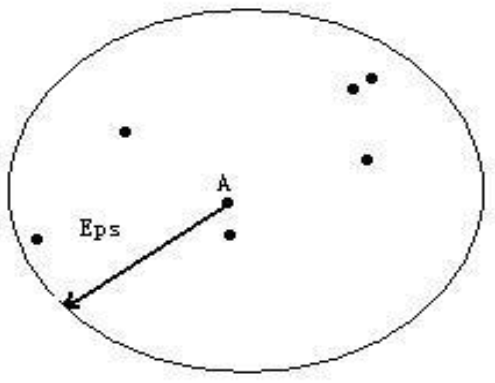

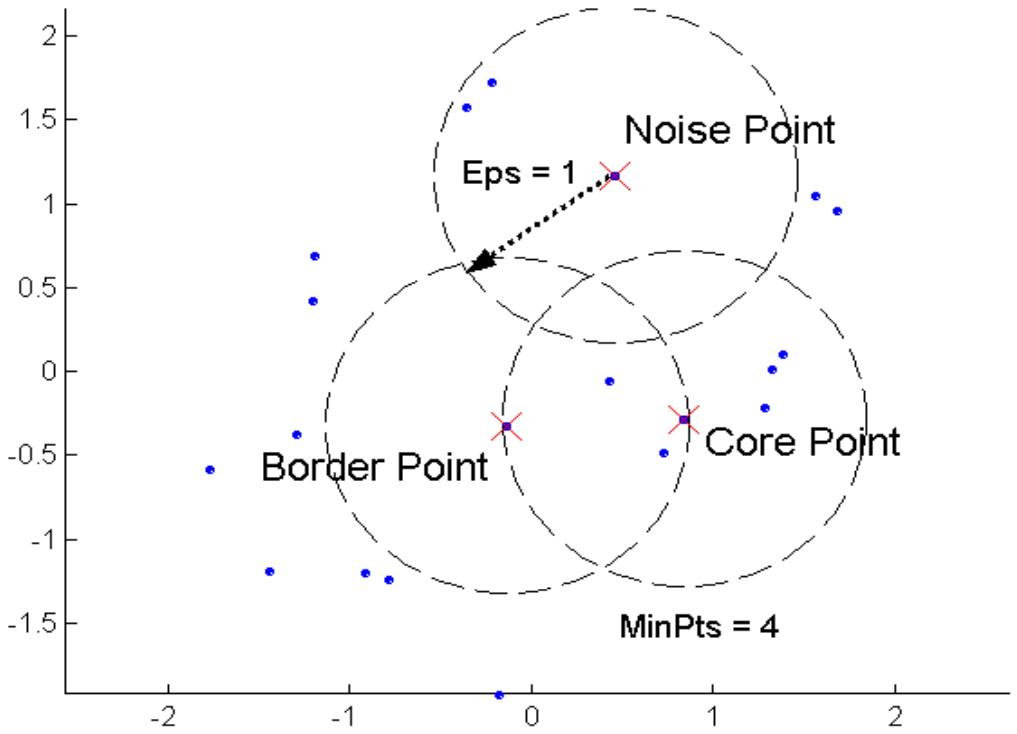
核心点（core point）：在半径内含有大于等于最小数目MinPts的点都是核心点；核心点在簇内，或者说在稠密区域内。是否为核心点，由Eps和MinPts决定。
边界点（border point）：稠密区域边缘上的点；边界点不是核心点，但边界点的Eps邻域内有核心点。
噪音点（noise point）：稀疏区域上的点，或者说任何既不是核心点也不是边界点的点。
直接密度可达（directly density-reachable）：如果x是核心点，y在x的Eps邻域内，则y是从x直接密度可达的。
密度可达：对于一组样本，如果是从直接密度可达的，则是从密度可达的。“链式反应”。
密度相连：如果样本点y和z都从x密度可达，则它们是密度相连的。

1.2算法步骤

• 【初始化】遍历数据点，计算每个点的Eps邻域；
• 【建簇】循环遍历数据点，判断它是不是核心点，如果是，就以它为圆心以Eps为半径画圆建簇，如果不是，就暂时归为噪音点；
• 【扩张簇】循环遍历簇内的点，判断它是不是核心点，如果是，就将其Eps邻域内的点都归入簇，如果不是，则不做额外操作，因为该点本身就属于簇，直到遍历完簇的所有点，这样簇得到了扩张。

算法的关键是依次处理每一个还未标记的样本点，反复扩张，直到找到一个完整的簇。最后DBSCAN算法会将样本划分成K个簇以及噪声点的集合。
DBSCAN中簇的定义为：一个簇中的任意两个样本都是密度相连的，如果一个新的数据点是从一个簇中的某个样本点密度可达，则这样新的数据点就属于这个簇。
DBSCAN不像K-Means那样需要用户指定中心点数目/簇的数量，但需要指定半径和最小点数，算法自动发现簇的数量。

2.DBSCAN：核心问题

2.1超参数的设置

样本点邻域的半径Eps：难以确定。如果是低维，可以通过散点图来判断；或者选择不同的Eps来对比聚类效果。
核心点的样本数阈值MinPts：如果样本向量是n维，则一般有：.
【问题】设置超参数中的矛盾：
如果希望聚类的类别较多，则核心点的数量应该更多，所以Eps应该更大，MinPts应该更小，但这样聚类，会将很多簇都合并到了一起，结果聚类的类别反而少了；
如果希望聚类的类别较少，则核心点的数量应该更少，所以Eps应该更小，MinPts应该更大，但这样聚类，会出现很多独立开的小类，结果聚类的类别反而多了。

2.2DBSCAN的缺点

• 聚类效果受距离函数影响大

在定义样本点x的Eps邻域时，需要计算其他点与x的距离，选用不同的距离函数会影响到聚类的质量。
而且当样本维数很高时，会有维数灾难的问题，计算量也很大。

• 超参数的人为设定比较困难

邻域半径Eps和样本数阈值MinPts的理想值不容易设定，这对聚类结果有很大影响。

• 运算量大，不便进行分布式

K-Means中数据样本点可以分布式计算到各个中心点的距离（需要将中心点的集合分发到各个节点），并进行所属类簇的标注以及更新中心点，将同一类簇的数据点进行聚合，如此迭代下去。但DBSCAN中没有使用中心点，通过距离计算样本点的邻域，运算量大，不适合进行分布式。

2.3DBSCAN优化加速

如何快速找到一个点的邻域以所有邻居的集合，可以用R树或KD树等数据结构加速。

3.DBSCAN：应用

3.1热点发现

由于热点是实时变动的，例如：新闻热点，并不能提前知道有多少类的热点，可用DBSCAN自动聚类。

3.2DBSCAN+K-Means

针对K-Means的受异常点/噪声点影响大的缺点，可以先用DBSCAN聚类，去掉噪声点，再对没有噪声点的数据进行K-Means聚类。

参考来源： 1.雷明《机器学习与应用》