KL距离（相对熵）

1. KL距离公式

KL距离：用来预测的概率和真实的概率之间的距离，度量概率分布的差异。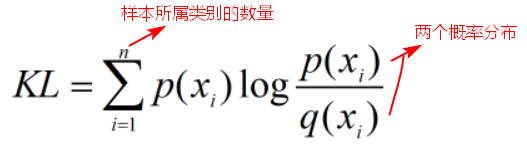
其中，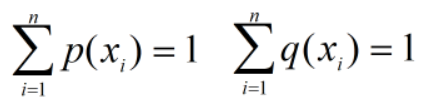

相对熵

相对熵(relative entropy, 或称Kullback-Leiblerdivergence, KL 距离)。
两个概率分布p(x) 和q(x) 的相对熵定义为：
, 该定义中约定。
相对熵常被用以衡量两个随机分布的差距。
当两个随机分布相同时，其相对熵为0。当两个随机分布的差别增加时，其相对熵也增加。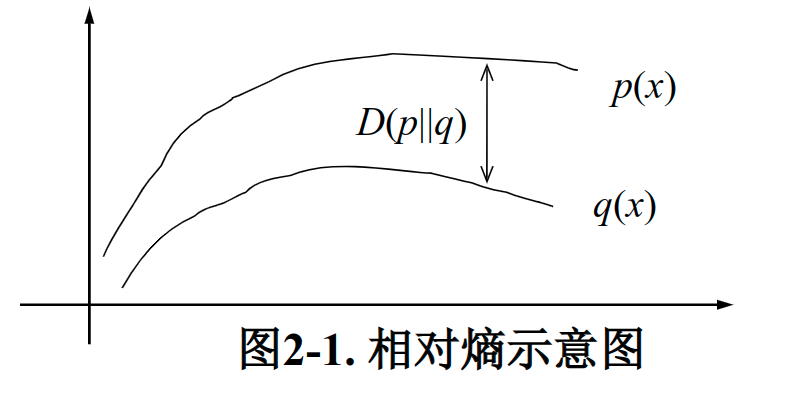

2.KL距离的特性

• 非对称性

【问题】以下哪个q的概率分布和p(x)的分布最接近？（即KL距离最小）

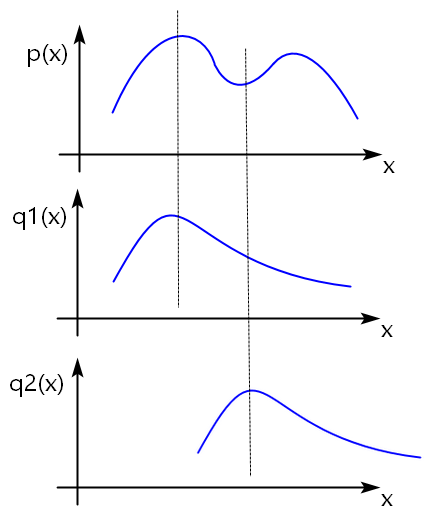
根据KL距离公式，，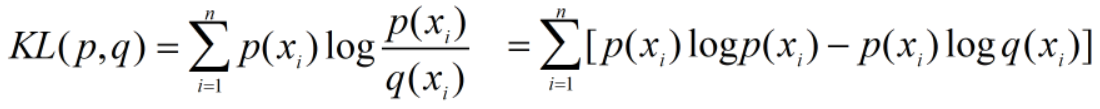
寻找相对于p(x)最近的分布，p(x)保持不变，要使KL距离最小，则需要 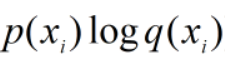越大越好。
因为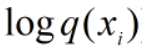为负数，
当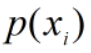取值较大时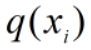，越大越好；当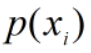较小时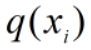，取值对距离影响较小。
所以，此时，q1(x)的分布和p(x)的分布更接近。

当KL距离公式为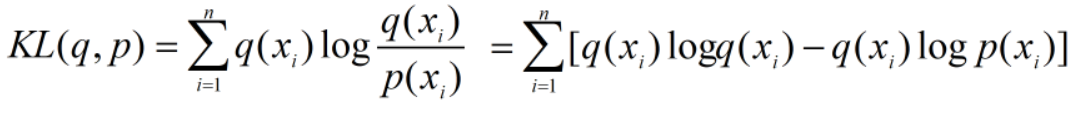：时，
因为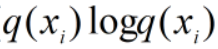 只和q自身有关，要使KL距离最小，则需要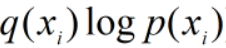越大越好。
当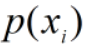取值较大时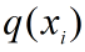，取值对距离影响较小；当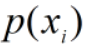较小时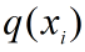，取值越小越好。

【结论】为了使KL距离更小，当KL(p,q)计算距离时，q要尽可能拟合p的大值；当KL(q,p)计算距离时，q要尽可能拟合p的小值。