一、向量
1.概念定义
向量中的元素
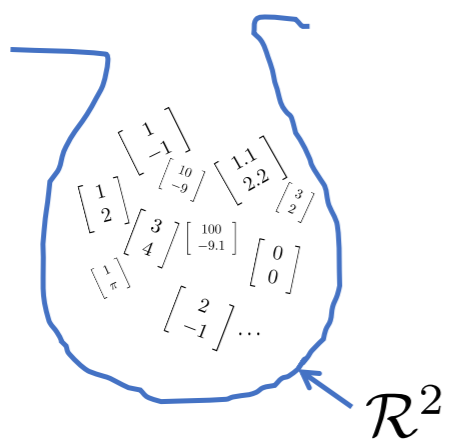
向量集合
向量集合就是以向量为元素的集合，元素的个数可以是无限个。写法举例：
如果某个向量集合中所有向量都有n个元素，则该向量集合记为
。
标准向量
如果一个向量中的其中一维是1，其他是0，这是一个标准向量（standard vector）。
2.向量属性
3.均值向量
向量随机变量X的数学期望也是一个向量，其各分量是原X各个分量的数学期望。
随机变量X的均值向量 μ定义为：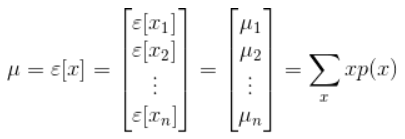
二、矩阵
1.概念定义
方阵Square
行数和列数相等的矩阵是方阵。m=n
以方阵为前提：对称矩阵、可逆矩阵、正交矩阵、特征值与特征向量、对角化、矩阵的迹。
转置矩阵（Transpose）
可以证明：转置操作是一个线性系统（Linear System）。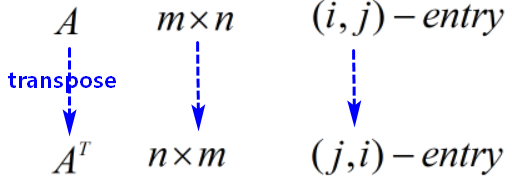
对称矩阵（symmetric）
对称矩阵是以主对角线为对称轴，各元素对称相等的矩阵。
对称矩阵是方阵，其转置和自身相等。各元素都为实数的对称矩阵是实对称矩阵。
对角矩阵（diagonal）
对角矩阵(diagonal matrix)是一个主对角线之外的元素皆为0的矩阵，对角线上的元素可以为0或其他值。（主对角线：n阶方阵中从左上角到右下角的斜线）
对角矩阵写为：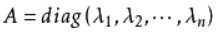
，
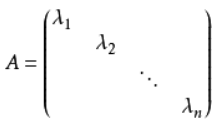
当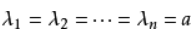
时，对角矩阵称为数量矩阵。
当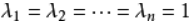
时，对角矩阵称为单位矩阵。
对角化**：对于一个n阶矩阵A，如果存在一个正交矩阵P，使得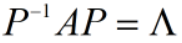
，这是矩阵A的对角化，称P为对角化旋转矩阵，
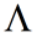为n阶对角矩阵。
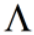的对角线元素为矩阵A的特征值（非负），矩阵P的列为矩阵A**的正交化特征向量。一个矩阵可以对角化的充分必要条件是存在一个线性无关的特征向量。实对称矩阵一定可以对角化。
正交矩阵（orthogonal）
一个n阶矩阵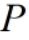
满足：
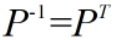，则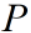
是正交矩阵。此时有：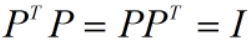
- 正交矩阵的行列式为1；
正交矩阵的行向量、列向量之间相互正交，不同行/列的内积为0，相同行/列的内积为1。
2.矩阵属性
3.协方差矩阵
协方差矩阵是一个对称的方阵（行数=列数），主对角线上是各个维度的方差（variance）。
- 协方差矩阵计算的是不同维度之间的协方差，在计算每个协方差时要用到各个样本。
- 计算一个样本矩阵的协方差矩阵，要明确一行是一个样本还是一个维度。维度之间的协方差（covariance）计算如下：
三、矩阵与向量
1.矩阵与向量相乘
线性系统
矩阵与向量相乘，可以看成是输入为向量，矩阵为参数的线性系统。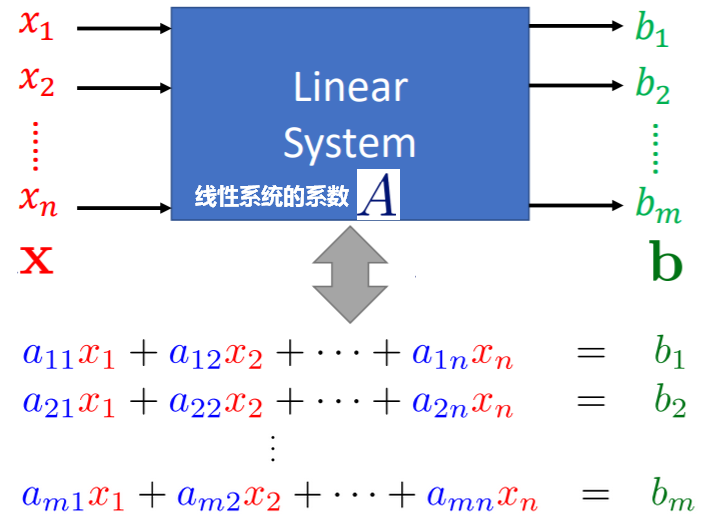
行角度
行角度的拆解形式，称为线性方程组（system of linear equation）。具体参见“线性系统”一节。
列角度
列角度的拆解形式，称为线性组合（linear combination）。具体参见“线性系统”一节。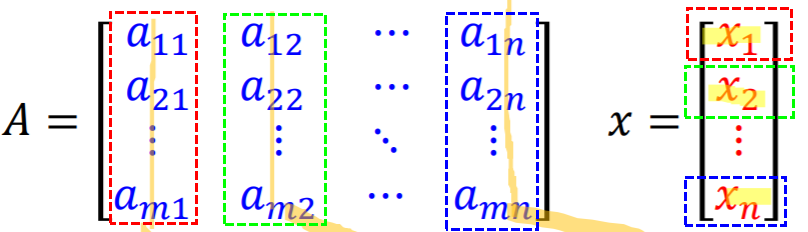
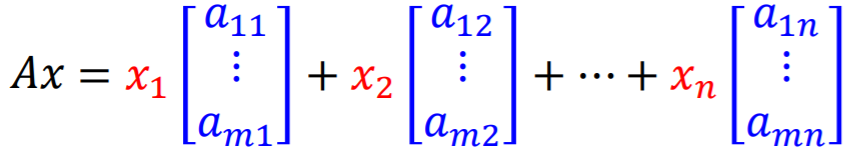
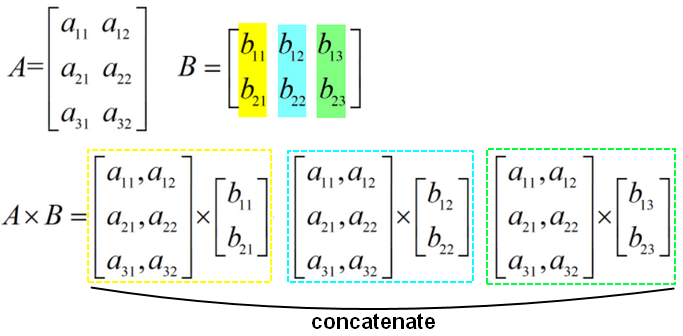
矩阵与矩阵相乘
2.范数（norm）
范数在机器学习中的作用：计算距离，衡量向量/矩阵的相似程度。
3.特征值/特征向量
对于 n 阶矩阵A，如果存在一个数 λ 和一个非0向量 x ，满足：
λ 是矩阵A的特征值（eigenvalue），x** 是特征值 λ 对应的特征向量（eigenvector）。（特征值/特征向量可以有多个。）
【性质1】如果 x** 是矩阵A的属于特征值 λ 对应的特征向量，那么对于
，k**x 也是矩阵A的属于特征值 λ 对应的特征向量。
【性质2】如果 x,y** 都是矩阵A的属于特征值 λ 对应的特征向量，那么对于
，a**x+by 也是矩阵A的属于特征值 λ **对应的特征向量。
- 矩阵A的一组特征向量是一组正交（orthogonal）向量（向量内积为0，相互垂直）。
- 矩阵A的所有特征值的和为矩阵的迹（trace）：
（n阶矩阵A的主对角线上各元素的总和被称为矩阵A的迹/迹数，
）
- 矩阵A的所有特征值的积为矩阵的行列式：
从矩阵线性变换角度，理解特征值和特征向量：
矩阵乘法对应了一个变换，是把任意一个向量变成另一个方向或长度都大多不同的新向量。在这个变换的过程中，原向量主要发生旋转、伸缩的变化。
如果矩阵对某一个向量或某些向量只发生伸缩变换，不产生旋转的效果，那么这些向量就称为这个矩阵的特征向量，伸缩的比例就是特征值。
【特征值、特征向量的应用】
通过求出方阵A的特征值和对应的特征向量，就能找到旋转后正确的坐标轴，得出使数据在各个维度区分达到最大（方差最大）的坐标轴。
在数据挖掘中，直接用特征值来描述对应特征向量方向上包含的信息量，而某一特征值除以所有特征值的和就为：该特征向量的方差贡献率（在该维度下蕴含的信息的比例）。
经过特征向量变换下的数据称为变量的主成分，当前m个主成分累计的方差贡献率达到85%以上就保留这个m个主成分的数据。实现了对数据进行降维的目的。
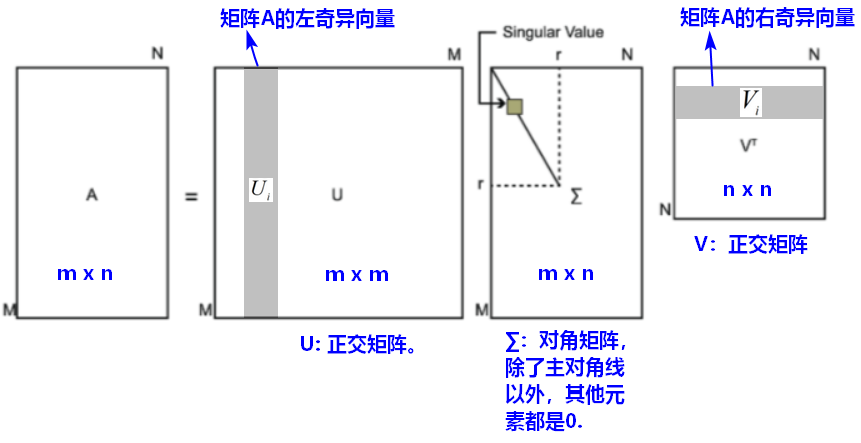
4.奇异值分解SVD
4.1完全奇异值分解
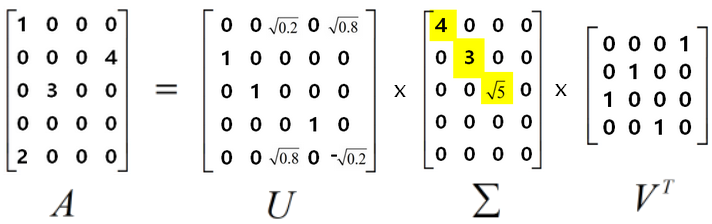
假设A是一个mxn的矩阵，则存在以下奇异值分解SVD（singular value decomposition）：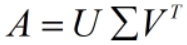
- 矩阵的奇异值分解一定存在，但不唯一：奇异值是唯一的，但矩阵U和V不是唯一的。
- SVD不要求矩阵A是方阵，SVD可以看成是矩阵的对角化的推广。
- ∑(矩形)对角矩阵的对角线元素是降序排列的非负元素（奇异值）。
- U是m阶正交矩阵，V是n阶正交矩阵，满足：
；
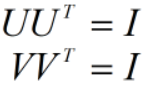左奇异向量是线性无关的，
；右奇异向量也是线性无关的，
；
4.2紧奇异值分解
紧奇异值分解（compact SVD）是与原始矩阵等秩的奇异值分解。
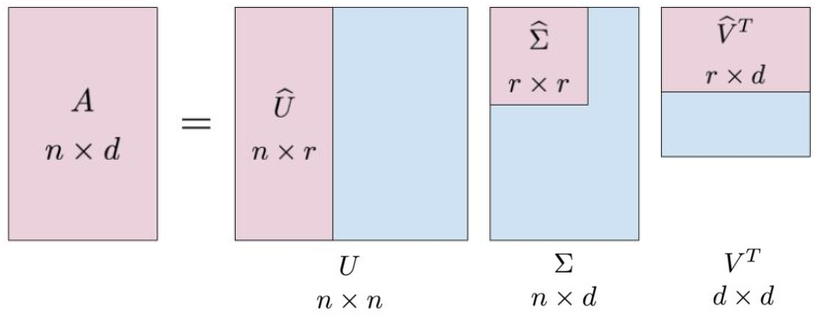
4.3截断奇异值分解
截断奇异值分解（truncated SVD）是比原始矩阵低秩的奇异值分解。
- 如果将
的主对角线元素
删除，即主对角线只剩
，令
，则：
， 
，
是所有秩为
的矩阵中最接近原矩阵
的矩阵，即两个矩阵的距离最小：
利用低秩矩阵估计（low rank approximation）可以对图片进行压缩。
在高维的情况下，前10%的奇异值平方和就占据了全部奇异值平方和的80%。依据奇异值能量占比选择k值：，一般取阈值为90%，这样达到了降维的目的。
4.4多角度理解SVD
【角度1：矩阵线性变换】
矩阵的奇异值分解，可以看做将矩阵线性变换分解为旋转变换（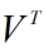
）、缩放变换（
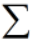）、旋转变换（
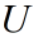）的组合，其中，旋转变换分别基于空间的标准正交基进行。
【角度2：矩阵对角化】
SVD是矩阵对角化的推广。对角化：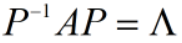
4.5奇异值分解的主要性质
mxn的矩阵A，SVD为：
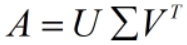
U的列向量（即左奇异向量）是
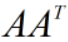的特征向量；V的列向量（
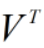的行向量，即右奇异向量）是
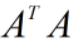的特征向量。∑的奇异值是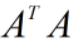或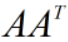的特征值的平方根。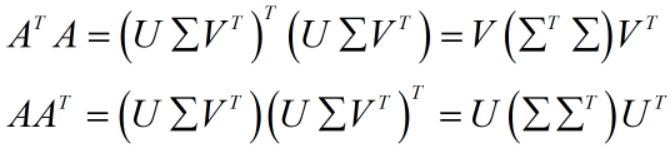
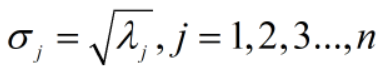
矩阵A的奇异值分解中，奇异值、左奇异向量、右奇异向量的关系如下：
矩阵A和∑的秩相等，等于正奇异值
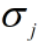的个数（包含重复的奇异值）。
当A是n阶方阵时，如果A有n个特征值，由n个特征值得到一个对角矩阵
，由n个特征向量生成一个n阶矩阵
，则
，将n个特征向量标准化之后，
，所以：
4.6奇异值分解的应用
矩阵压缩
使用截断奇异值分解，如果选择的前k个奇异值占所有奇异值的比例足够大，得到的新的矩阵和原矩阵非常接近。这其实是类似于图像压缩，只保留图像分解后的两个方阵和一个对角阵的对角元素，就可以恢复原图像。
数据降维
利用SVD来实现PCA降维。
协同过滤
协同过滤包含基于用户的协同过滤，基于物品的协同过滤。这两种方式本身是不需要SVD就可以进行的；但是加入了SVD之后，可以减少计算量同时还能提高推荐效果。
将用户x商品的矩阵分解为三个矩阵（用户x隐变量，用户隐变量x商品隐变量，商品x隐变量），求出用户隐变量和商品隐变量之间的映射关系。
若有收获，就点个赞吧
0 人点赞
