梯度下降

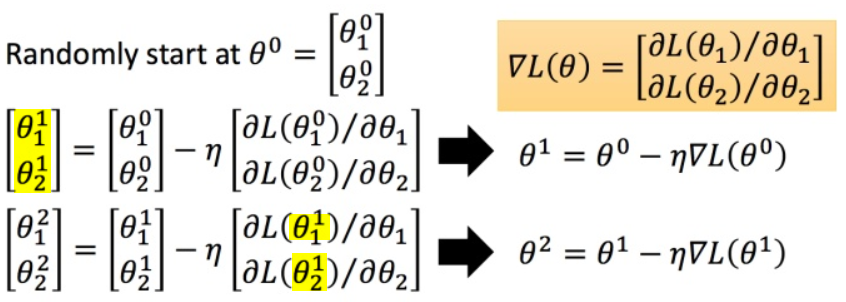
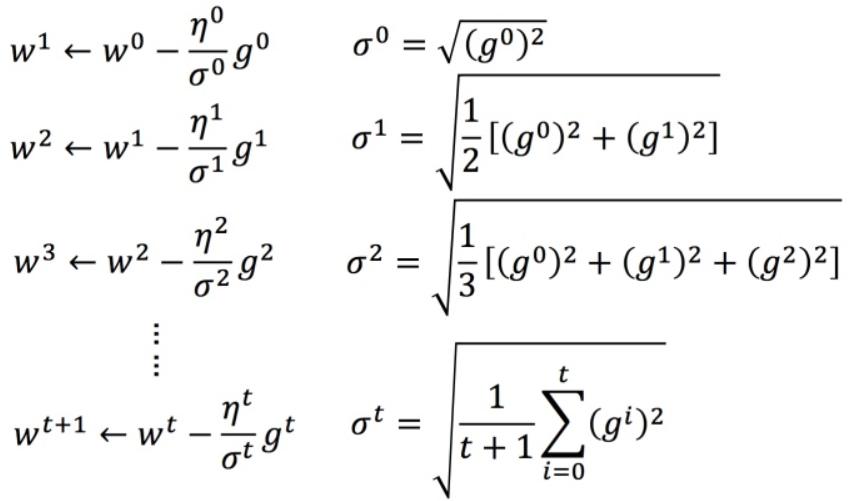1.梯度的理解

1.1梯度的含义

对多元函数求偏导数形成的向量就是梯度。
梯度是一个向量组合。

1.2梯度下降的三要素

• 出发点（参数初始值）
• 下降方向
• 步长/学习率

1.3梯度下降的理论推导

如果没有章法的进行梯度下降，每次更新参数之后的loss并不一定会越来越小。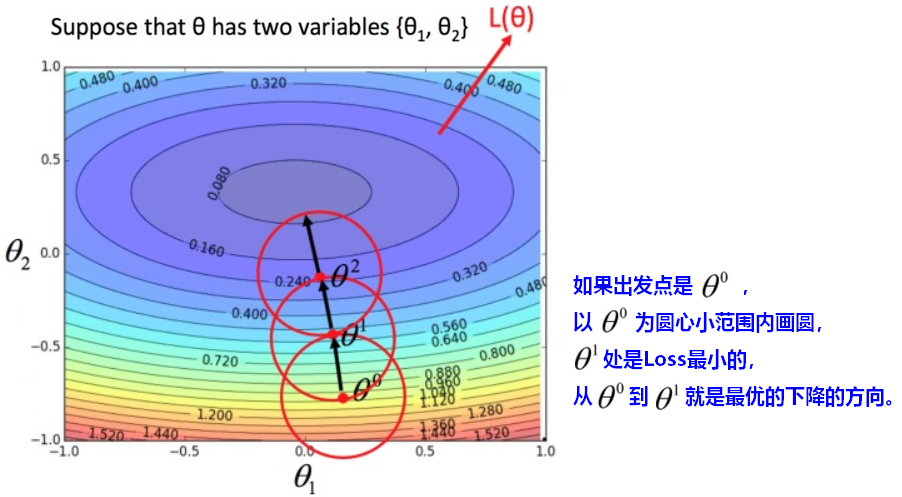

【问题】如何在圆圈内，快速找到Loss最小值？
在 (a,b) 点的红色圆圈内（圆圈足够的小），可以将损失函数用多变量泰勒展开式进行简化：


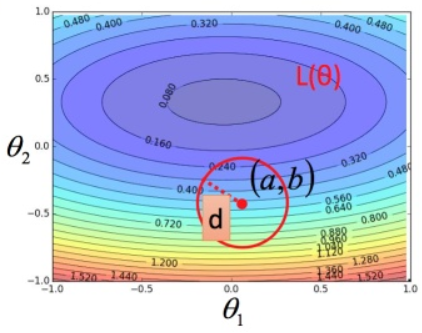
目标是最小化Loss，常数项 s 和调参无关，所以目标变成：

最小化 ，即最小化 向量(△θ_1,△θ_2) 和(u,v) 的内积（数量积）。

根据余弦值最小，要使两个向量内积最小，两向量的方向应该正好相反。
此时，有：

注意

• 以上推导梯度下降公式的前提是圆圈的半径足够的小（即学习率足够小），才能利用泰勒展开：

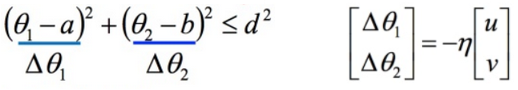
• 梯度下降的公式推导中，只保证了往下坡的方向走，并不保证是往最低点走，也不保证更新参数后得到的Loss一定会越来越小。

【问题】如何优化梯度下降，更快更准的找到最低点？
【调整出发点】选择合适的出发点。
【调整山坡和方向】向着最低点迈进，更快效率的更新参数。（特征归一化）
【调整学习率】学习率针对参数和更新次数做调整适应，保证尽量不提前停止或跑过。
【调整步长】寻找最佳步长。（Adagrad）

2.优化器（optimizer）

【问题】每次下降之后，梯度绝对值越来越小，更新之后更接近loss最低点，如何调整学习率？为什么需要调整学习率？
在坡度平缓的地方，梯度较小，但我们希望下降快一些，所以需要大一点的学习率；在坡度陡峭的地方，梯度较大，但我们希望下降慢一些，需要更小的学习率。

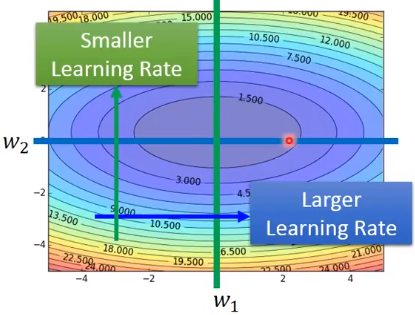
【期望1】随着次数的增加，通过一些因子来减少学习率。初始点会距离loss最低点比较远，所以使用大一点的学习率；越来越接近最低点了，此时减少学习率。
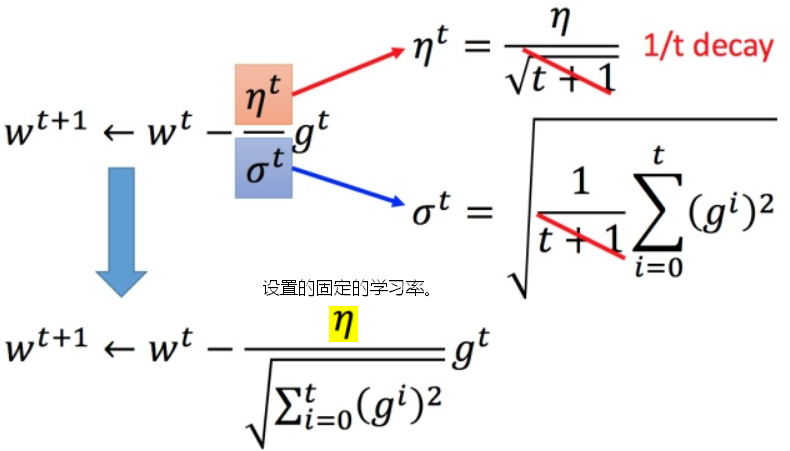
【解决1】令学习率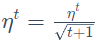，t 表示更新次数，学习率会随着更新次数而逐渐减小。
【期望2】不同参数的更新，使用不同的学习率，而不是共用一个学习率。
【解决2】Adagrad

2.1 Adagrad

自适应学习率

对于参数 w，梯度为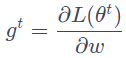，普通梯度下降的学习率为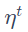，Adagrad的学习率为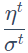

参数更新为：，
为之前对该参数求的所有偏导的均方根。
【举例】

Adagrad的简化

Adagrad理论解释：归一化+最佳步长

Adagrad计算步长时，有矛盾存在，梯度变大，会导致步长变大，此时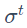变大，又会减小步长。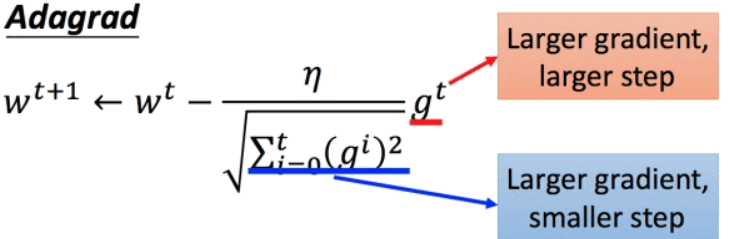

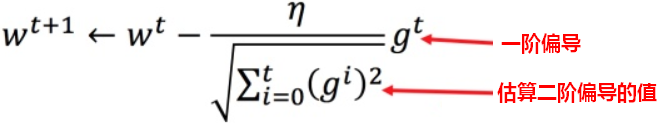
【结论1】最佳步长是 一阶偏导数/二阶偏导数，Adagrad体现了最佳步长。
【举例】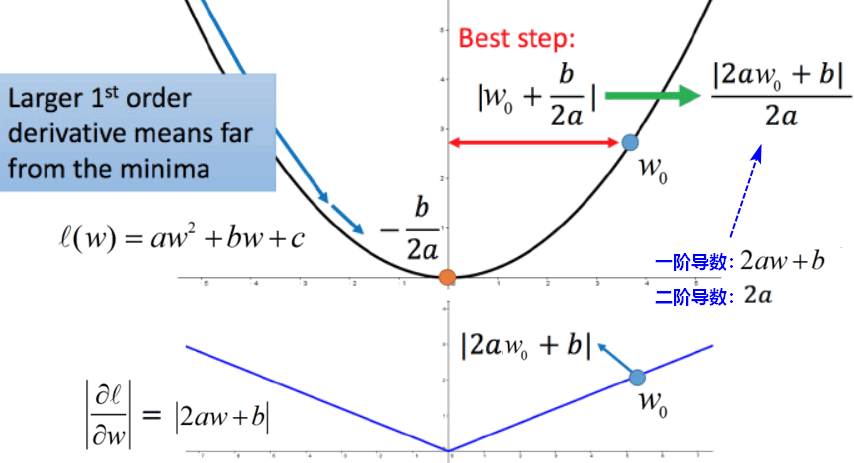


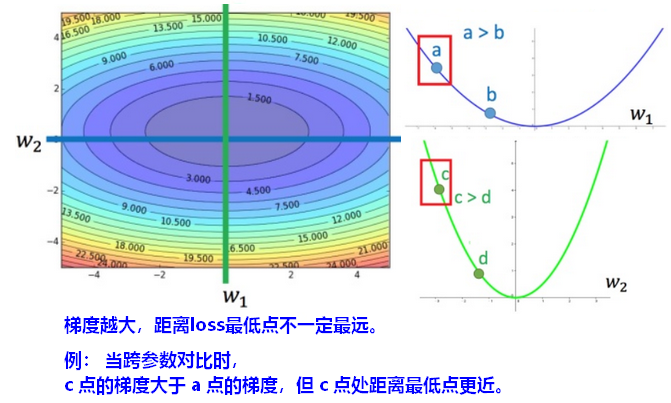
【结论2】Adagrad记录了各维度梯度的量级，相当于统一了梯度的量级，减小了下降时路径的震荡，Adagrad的本质是数值归一化。
用r记录梯度量级，有：， 。

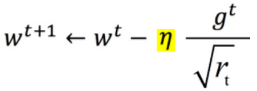Adagrad的问题和效用

效用：Adagrad有自适应学习率，可以调整梯度。
当w2方向上比较陡峭时，我们希望下降的慢一些，此时梯度大，Adagrad的学习率较小，下降的慢；
当w1方向上比较平缓时，我们希望下降的快一些，此时梯度小，Adagrad的学习率较大，下降的快。
问题：随着迭代次数增多，记录梯度量级的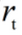会越来越大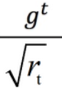，趋近于0，导致梯度更新变慢。

2.2 RMSProp

对于神经网络中更为复杂的损失函数图像，即使是同一个方向上，梯度下降也有快有慢，此时Adagrad不太适用。我们需要更为动态变化的学习率。
【问题】神经网络中，梯度下降，如何避免取到局部最优解？
经研究，神经网络中的损失函数是比较平滑的，一般得到的最优解就是全局最优解，或者非常接近全局最优解。
另外，用于解决局部最优解的方法是，加入物理学中的“惯性”概念。

RMSProp的理论解释

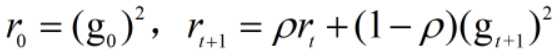
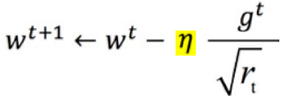
RMSProp对梯度进行了加权求和，只保留过去给定窗口大小的梯度，解决了Adagrad在后期梯度更新变慢的问题，加快了收敛。

2.3 Momentum：动量

原本梯度下降是走梯度向量的反方向（详见梯度的理论推导），为了尽量避免走入局部最优解，在每一次下降过程中，考虑上一次下降方向对本次下降的影响（即“惯性”）。

每一次梯度下降的方向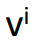，实际上是之前所有梯度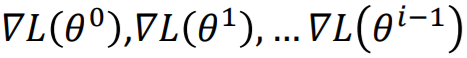的加和，受之前所有梯度的影响。可以看出，受最近的梯度影响较大。
动量法，可以使梯度下降在梯度方向不变的维度上更新更快，在梯度方向有所改变的维度上更新变慢，可以加快收敛并减小震荡。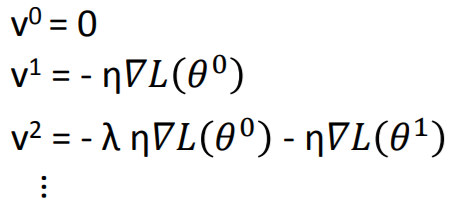

【注意】加入动量（Momentum）并不一定保证可以找到全局最优解，只是为找到全局最优解提供了更多可能。

2.4 Adam：RMSProp+Momentum

Adam理论解释

在Adagrad、RMSProp、Momentum中，动量v和量级r的初始化都为0。
Adam结合了RMSProp和Momentum的优点，m代表动量，v代表量级。
随着更新次数n增大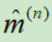，和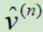会越来越小，初始化时，放大了m和v。

3.特征转换

3.1 问题引出

当输入的特征项之间量纲scale不一致，例如：
x2的量级大于x1的量级，当 _w_1 和 _w_2 做同样的变化时，
_w_1 对 y 的变化影响是比较小的，对loss的影响也比较小，w1方向上的坡度比较平滑。
w2对 y 的变化影响是比较大的，对loss的影响也比较大，w2方向上的坡度比较陡峭。
此时更新参数，两个方向上需要有不同的学习率。
【解决】使特征项之间的scale一致。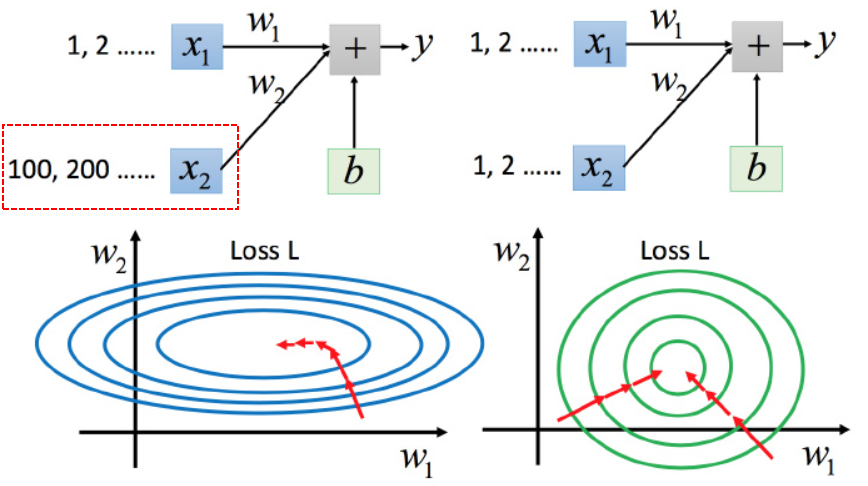

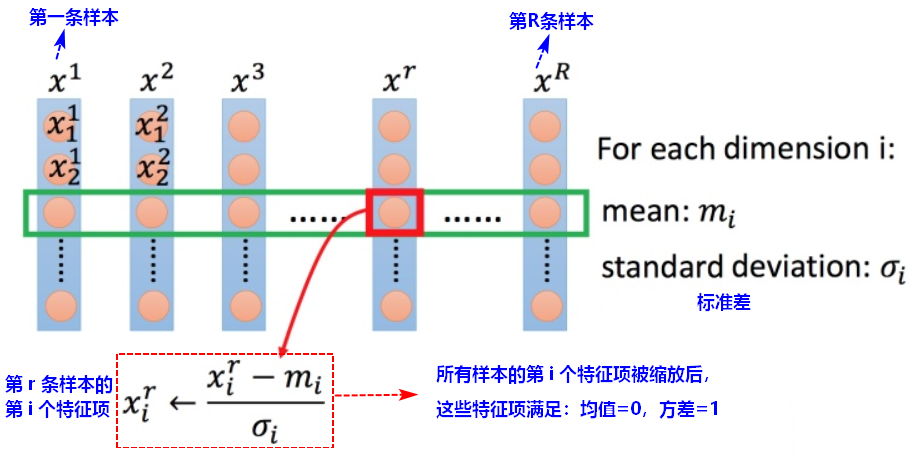
3.2 特征缩放(Feature scaling)

归一化的效果是让梯度下降朝着最低点走，参数更新得更有效率，目的是提高迭代求解的收敛速度和精度。

标准归一化

最大最小值归一化

x = (x-min)/(max-min)
【缺点】

• 当有新数据加入时，可能导致max和min的变化，需要重新定义。
• 对于outlier非常敏感，outlier影响了max或min值，所以这种方法只适用于数据在一个范围内分布的情况。
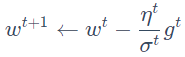