PCA降维

1.降维：

1.1降维的原因

维度灾难，维度冗余 >>> 降维

密采样：dense sample

当训练样本的采样密度足够大时，在任意测试样本x附近任意小的距离范围（σ）内，总能找到一个训练样本。
当样本的属性维数n越来越大时，为了满足密采样条件，需要的样本数量也会指数级的增长。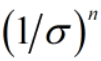
在高维的情况下，会出现数据样本稀疏、距离计算困难等问题。

降维：dimension reduction

通过数学变换，将原始高维属性空间转变为一个低维子空间（subspace），子空间中的样本密度大幅提高，距离计算也变得容易。

1.2降维方式

特征抽取/映射

把高维空间的数据，映射到低维空间。常用的降维方法有线性降维，如：PCA。

特征选择

1.3线性降维

基于对原始高维空间进行线性变换来降维的方法称为线性降维，线性降维的基本形式为：

原始维度是维，对原始高维空间线性变换之后，得到低维空间的维度是维，

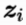• 是原属性向量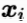在新坐标系中的坐标向量。

，，

• 新空间中的属性是原空间中属性的线性组合。
• W为变换矩阵（有个维基向量），如果新坐标系是正交坐标系，则W为正交变换。

• 对W施加不同的约束，即对低维子空间有不同的性质要求，此时得到不同的线性降维方法。

  2.主成分分析PCA

  主成分分析PCA（Principal Component Analysis）降维是在做特征映射，属于线性降维方法，它要求低维子空间对样本具有最大可分性。

  2.1PCA降维思路

  主成分分析等价于对原坐标系进行坐标系旋转变换，将数据投影到新坐标系的坐标轴上。
  如果存在一个超平面对（正交属性空间中的）样本点进行表达，希望这个超平面：

• 最近重构性：样本点到超平面的距离足够近（最小投影距离）。

• 最大可分性：样本点在超平面上的投影尽可能分开（最大投影方差）。
• 原数据经正交变换成若干个线性无关的新变量表示的数据，即降维之后不同维度的相关性为0。

通过主成分分析，可以用主成分近似的表示原始数据，对数据降维，发现数据的基本结构（例如：考察因子负荷量、贡献率）。
【理解】为什么投影方差要最大？
样本数据投影后，应该保留尽可能多的信息量，即数据在所投影的维度具有尽可能大的区分度，这个信息量/区分度用投影后的方差来衡量。
【理解】为什么投影距离需要最小？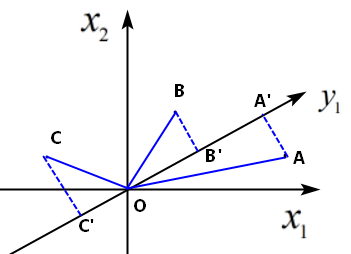
对x1,x2坐标系旋转，得到新的坐标轴y1，样本点在y1上有三个投影，投影点在y1上的方差和为：OA’^2+OB’^2+OC’^2，主成分分析要选择正交变换后投影方差最大的，根据勾股定理，则需要投影距离（AA’^2+BB’^2+CC’^2）最小。

【理解】为什么PCA降维要进行正交变换？
对原数据进行变换，期望变换后没有维度冗余，且新变量之间线性无关，这样才能降低分析的难度；只有当新坐标系为正交坐标系，即经过正交变换，各主成分之间正交，才能消除可能出现的低秩（low-rank低秩代表矩阵行或列之间存在线性相关，每列/行可由其他列/行线性表示出，即存在冗余信息），新变量之间线性无关（协方差cov(y1,y2)=0）。

2.2PCA算法

输入：m x n样本矩阵X（m个属性维度，n条样本），对样本数据进行规范化处理，每一行元素（每一行代表一个属性）的均值为0。
输出：k x n样本主成分矩阵Y。（样本维度由m降到k，主成分个数为k个。）
主成分分析的目的是降维，一般选择个主成分（线性无关）来代替原有变量（线性相关），既可以简化问题，又保留了原有变量的大部分信息（原有变量的方差）。

样本规范化/白化

原样本由实数空间（正交坐标系）中的点表示，规范化处理后，数据会落在原点附近，均值为0，方差为1。

总体主成分分析

在数据总体上进行的PCA称为总体主成分分析。
【定义】


如果满足以下条件：
1)是一组标准正交基，即向量是单位向量，；
2)变量与变量互不相关，即；
的第一主成分：是的所有线性变换中方差最大的，则是第一主成分。
的第二主成分：是与不相关的的所有线性变换中方差最大的，则是第二主成分。
一般的，是与都不相关的的所有线性变换中方差最大的。
【主成分的求解、性质】
根据定义，如果是的第主成分，，则方差最大，有
，定义拉格朗日函数求解约束最优化问题可得：
，

• 所以是的第大特征值，是该特征值对应的单位特征向量。
• 总体主成分的协方差矩阵是对角矩阵：

，并且

• 的协方差矩阵满足：

令为正交矩阵，，

• 总体主成分的方差之和等于随机变量的方差之和：

总体主成分的方差之和，就是协方差矩阵的主对角线元素之和（迹trace）；
随机变量的方差之和，就是协方差矩阵的主对角线元素之和（迹trace）；

【问题】如何求解特征值λ和特征向量α，来完成PCA降维？
在中，，
是原样本数据矩阵中各个元素减去各自所在维度的均值后得到的矩阵，n为样本数量。
奇异值分解：，右奇异向量就是的特征向量，奇异值的平方就是对应的特征值，即求出了，就可以用线性变换求解各个主成分。

因子负荷量

第k个主成分与变量的相关系数称为因子负荷量：（表示两者之间的相关程度）

选择主成分的个数

通常利用方差贡献率选择主成分的个数k。
第k个主成分的方差贡献率是的方差与所有方差之和的比：，
k个主成分的累计方差贡献率为：，
累计方差贡献率反映了主成分保留信息的比例，通常取k使得累计方差贡献率达到规定的百分比之上。（70%~80%）

样本主成分分析

在有限样本上进行的PCA称为样本主成分分析。
定义有限样本（n条观测样本，每条样本都是m个维度）：
，随机变量
表示第j条观测样本的第i个变量。
样本协方差矩阵S为：，（计算协方差时，每条样本都参与计算）

2.3核主成分分析

核主成分分析（Kernelized PCA）KPCA：现实任务中，可能需要非线性映射才能找到合适的低维嵌入（而不是线性变换）；如果先从本真的低维空间采样并嵌入高维空间，此时如果直接使用线性降维，会丢失原本的低维结构。非线性降维的常用方法是基于核技巧对线性降维方法进行核化（kernelized）。
通过将样本映射到高维空间（从维到维），再在高维特征空间中实施PCA（从维到维）：
其中：
，高维空间的映射虽然不清楚具体形式，但可以引入核函数：

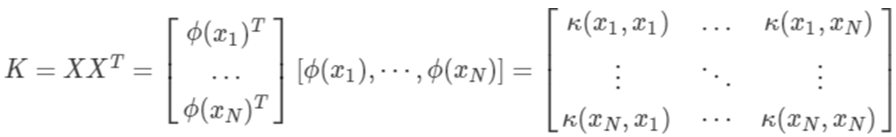
2.4PCA的优缺点

主成分分析的结果可以用于其他机器学习方法的输入。
PCA的主要优点：
（1）仅通过方差衡量信息量，不受数据集以外因素影响。
（2）各主成分之间正交，消除可能出现的低秩、或者原始数据成分间相关的可能。
（3）计算方法简单，易于实现。
PCA的主要缺点：
（1）降维后各个特征维度的含义具有一定的模糊性，数据的可解释性没有原始样本的特征强。（可解释性变弱）
（2）方差小的非主成分可能含有对样本差异的重要信息（可能丢失强力特征），因降维丢弃后可能对后续处理有影响。

参考来源： 1.周志华《机器学习》 2.李航《统计学习方法》（第2版）