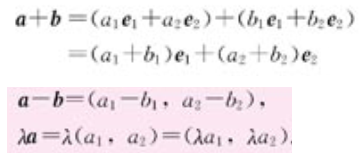一、数学知识
1.概念
向量:有大小、方向的量。
有向线段:向量的直观表示。线段的方向表示向量的方向,长度表示位移的距离,即向量的长度。
相等的向量:同向且等长的有向线段。
基线:通过向量的直线,叫向量的基线。
向量共线或平行:向量的基线相平行或重合,则称这些向量共线或平行。平行向量的相应坐标成比例。
向量互相垂直:两个向量的基线相互垂直。
单位向量:与一个非零向量同向且长度为1的向量,称为这个非零向量的单位向量。
基向量:与轴(规定了长度单位与方向的直线)同向的单位向量e,称为轴的基向量。
坐标/数量:对轴上任一向量a,存在唯一实数x,使得a=xe,则称 x 是 a 在轴上的坐标/数量。坐标的意义是在实数和向量之间建立起了一一对应关系,于是可以用数值来表示向量,进而把平面/空间向量数值化、代数化。
基底:一个平面内不共线的一组单位向量,叫做这个平面内所有向量的基底。
正交基底:作为基底的两个基向量相互垂直,则这个基底称为正交基底。
正交分解:在正交基底下分解向量,称为正交分解。
直角坐标:对于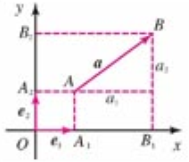 ,有
,有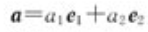 ,则
,则 
有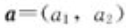
数乘向量:实数λ与向量a的乘积仍然是一个向量,记为λa。
向量的数量积

向量的数量积是一个实数。
2.公式法则
向量的线性运算
- 向量求和的三角形法则:
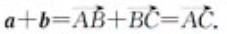
动点从A到C的位移等于从A到B,再从B到C的位移之和。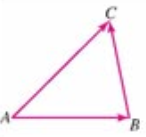
- 向量加法交换律:
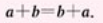
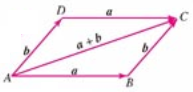
- 向量加法的平行四边形法则 / 向量加法的结合律:
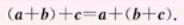
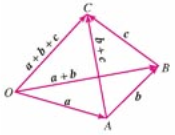
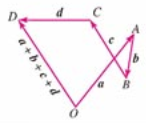
- 向量的多边形法则:以第一个向量的始点为始点,以第n个向量的终点为终点的向量,叫这n个向量的和向量。
- 数乘向量运算:
向量的坐标运算
- 对于轴上两个向量:
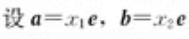 ,有:
,有:
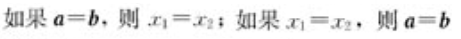
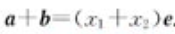
- 轴上向量的坐标=终点坐标-始点坐标。
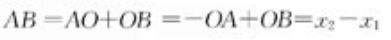
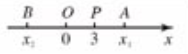
- 向量的直角坐标运算:
向量的数量积/内积
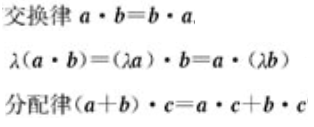
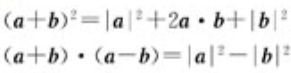
- 向量数量积的坐标运算
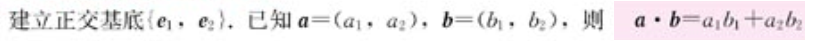
- 向量的长度

n维向量的坐标运算

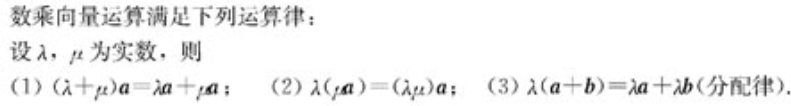
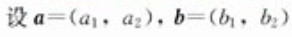 ,有如下结论:
,有如下结论: