1.深度
1.1为什么需要深度?
deep vs shallow
shallow网络,不断增加参数,也可以增加space;fit同样的function,deep网络需要的参数量比较少。
shallow网络的神经元需要多少才能拟合一个f?
理论上,只有一个中间层的神经网络,只要神经元的数量足够多,就可以拟合任意的函数曲线。但为什么还需要深度神经网络?
- 经实践证明,又深又窄的网络模型的预测效果要好于又浅又宽的网络模型。
- 只有一层的足够宽的网络,参数是海量的,未必能找出。
- 深度网络自带特征提取,每一层相当于进行特征组合,层数越多,特征组合能力越强。
- 深层网络集成了多个小的函数模型,相当于进行了集成学习。
深层网络只代表网络具有学习潜力,但实际还存在学习障碍,有待解决。
2.激活函数
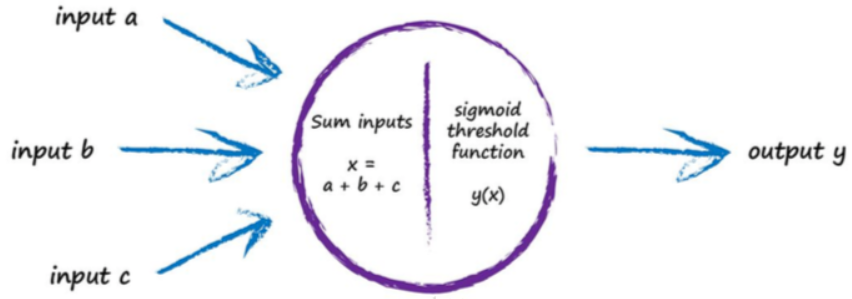
【问题】激活函数的设置,为什么以层为单位,而不是以神经元为单位去设置?
如果同一层中不同的神经元设置不同的激活函数,理论上可以,但GPU不擅长逻辑判断每一个神经元该使用什么激活函数,所以实际中每层的神经元使用一样的激活函数。
2.1好的激活函数
好的激活函数应该具有如下特点(不要求全部满足):
- 非线性
理论上,只要是非线性函数,都可以作为神经网络中神经元的激活函数。
如果不用激活函数或仅使用线性函数,则每一层的输出都是上一层的线性组合,从而导致整个神经网络的输出为神经网络输入的线性组合(多层线性相乘等价于一层,退化成单层线性网络),无法逼近任意函数,拟合能力差。
一个函数图像中,只要有一个输入点可以体现非线性,这个函数就是非线性的,例如:ReLU.
- 零均值(zero-centered)输出
0均值输出是指输出是关于原点对称的。
某一层的输出是下一层的输入,假如下一层将上一层非0均值的信号作为输入,则下一层求梯度: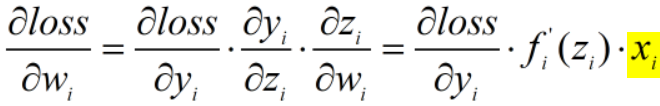 导致反向传播更新参数时,参数都朝同一个方向更新(同增/同减),产生捆绑效果,使得求极值的过程收敛变慢。
导致反向传播更新参数时,参数都朝同一个方向更新(同增/同减),产生捆绑效果,使得求极值的过程收敛变慢。
- 具有单调性
激活函数如果不具有单调性,对单个神经元来讲,输入变化(w变化)导致输出发生震荡(忽大忽小),整个网络也会发生震荡,求梯度时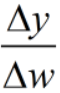 梯度方向会经常改变,收敛变慢。
梯度方向会经常改变,收敛变慢。
激活函数具有单调性可以减少输出的震荡。
- 输出范围有限
有限的输出范围使得网络对于一些比较大的输入也会比较稳定,但这需要trade-off,输出稳定会限制网络的表达能力,也可能导致梯度消失(区间饱和,使得参数无法继续更新);但如果输出没有上界,输出无限增大会导致溢出。
输出范围有限的激活函数一般用于某些特定场合,比如概率输出、LSTM里的gate函数等。
- 可微性且导数值适当
根据梯度消失、梯度爆炸的定义,反向传播求梯度时,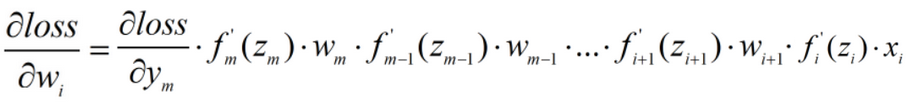
激活函数的导数值如果太小(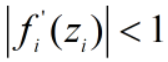 ),易发生梯度消失(gradient vanishing),越往前(靠近输入层),求出的梯度数值越小;
),易发生梯度消失(gradient vanishing),越往前(靠近输入层),求出的梯度数值越小;
激活函数的导数值如果太大(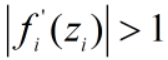 ),易发生梯度爆炸(gradient exploding),越往前(靠近输入层),求出的梯度数值越大。
),易发生梯度爆炸(gradient exploding),越往前(靠近输入层),求出的梯度数值越大。
梯度消失和梯度爆炸的根源在于各层导数值的量级不协调。
- 参数少,没有超参数
如果激活函数存在超参数,需要人为设定,增加了计算复杂度和使用难度。
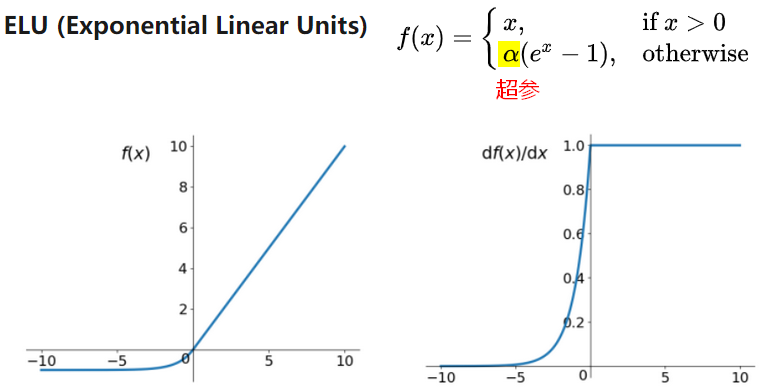
例如:Elu,Prelu都有超参数,设置起来比较麻烦,没有固定的准则。
- 运算速度快
激活函数在神经网络前向的计算次数与神经元的个数成正比,简单的非线性函数更适合用作激活函数。
2.2激活函数对比
- ReLU
神经网络中一般使用relu作为激活函数。
x<0 时,输出为0,神经元死亡,神经元死亡分为真死(不管输入怎么变,输出都为0)和假死(输入不同,输出可能不为0),神经网络中大部分情况都是假死。当某层有神经元死亡时,ReLU相当于有了特征选择的能力。(神经元死亡是指神经元不被激活,对应的参数无法更新)
当某层全部输出都为0时,神经元全部死亡,后面的若干层神经元也都会死亡,这种情况是不允许的。
x>0 时,输出为正数,导数为1,梯度不会层层衰减,可以解决梯度消失问题;但如果每一层输出都是正数相乘相加,最后结果太大可能会溢出。
若某层神经元的个数为M,该层神经元全部死亡的概率为P,则P与M成反比,即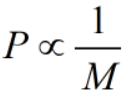 ,当神经元足够多时,该层神经元都死亡的可能性就趋近于0了;
,当神经元足够多时,该层神经元都死亡的可能性就趋近于0了;
若神经网络的层数为N,则某一层神经元全部死亡的概率为: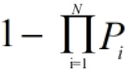 ,即层数越多,某一层神经元死亡的概率越小。
,即层数越多,某一层神经元死亡的概率越小。
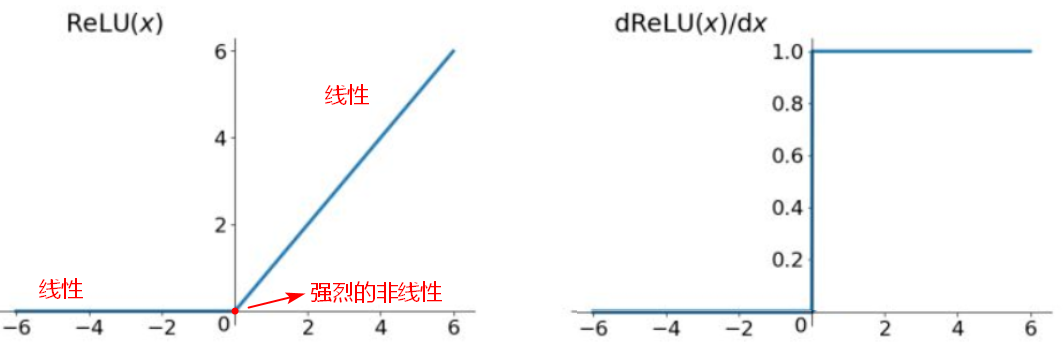
为了解决ReLU的神经元死亡问题,有一些ReLU的变种,例如:Leaky ReLu,PReLU,ELU等。
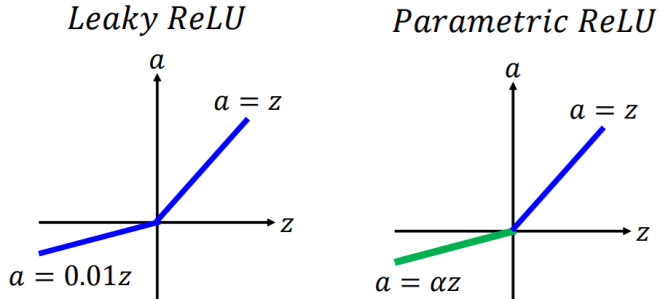
- ELU、LReLU、PReLU
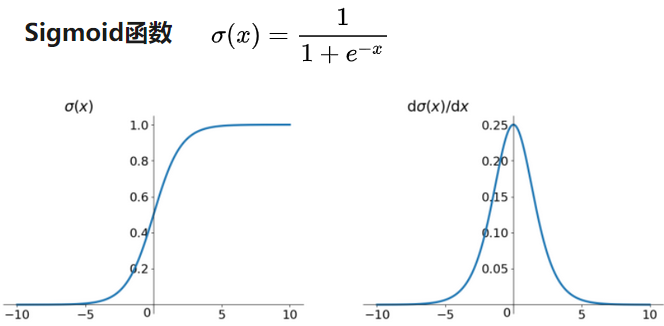
- Sigmoid
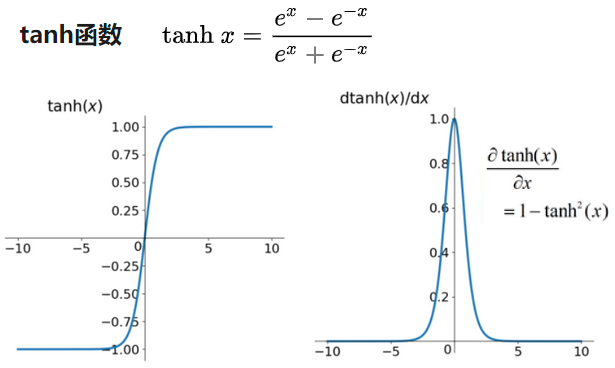
- tanh
| 非线性 | 0均值 | 单调性 | 输出范围 | 导数 | 参数 | 计算 | |
|---|---|---|---|---|---|---|---|
| ReLU | 非线性 | 否 | 是 | 0; 0~+∞ |
0或1 (解决了梯度消失问题) |
无 | 简单 快 |
| ELU | 非线性 | 近似 | 是 | -∞~0; 0~+∞ (解决神经元死亡问题) |
0~1 | 超参 | 复杂 |
| LReLU PReLU |
非线性 | 近似 | 是 | -∞~0; 0~+∞ (解决神经元死亡问题) |
α相关 | 超参 | 简单 |
| maxout | 非线性 | 可能 | 可能 | 无上下限 | w相关 | 无 | 复杂,量大 |
| Sigmoid | 非线性 | 否 | 是 | 0~1 | 0~0.25 | 无 | 复杂,耗时 |
| tanh | 非线性 | 是 | 是 | -1~1 | 0~1 | 无 | 复杂,耗时 |
| sin/cos | 非线性 | 是 | 否 | -1~1 | -1~1 | 无 | 复杂,耗时 |
3.梯度下降优化
3.1损失函数图像的特点
深度神经网络中,损失函数的图像“地形”非常复杂,
理论上存在极小值,但工程实践中,很难优化收敛到最优解;一般损失下降到可接受的范围即可。因为,经研究,神经网络中损失函数曲线是比较平滑的,经优化得到的解会比较接近最优解。
损失函数如果有极小值,则必然存在多个数值相等的极小值,即多个W的不同的解,对应的极小值是一样的。(证明:根据神经网络中梯度的求解公式,存在多个W相乘,如果有两个W,W1放大n倍,W2缩小1/n倍,相乘的结果没变,但W改变了。)
综上,深度神经网络的损失函数图像有如下特点:
- 地形复杂,但整体比较平滑;
- (如果有极小值)存在多个极小值;
- (高维情况下)存在很多鞍点;
虽然很难收敛到最优解,但经过优化方法后得到的解是接近最优解的。
3.2典型地形分析
3.2.1鞍点
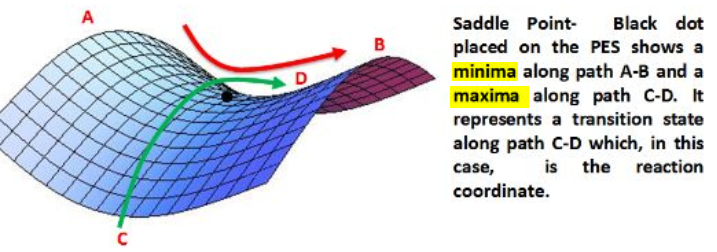
一阶导数可以说明函数的单调性,二阶导数决定了函数的凸凹性。二阶导数>0,则为凸函数,驻点处为极小值;二阶导数<0,则为凹函数,驻点处为极大值。
在鞍点(saddle point),二阶导数在各个方向上的符号不一致。
假设n维空间中,在每一维方向上,二阶导数>0的概率为P,二阶导数<0的概率为(1-P),某一点为鞍点的概率为:**P(鞍点)=1-P(极小值)-P(极大值)=1-P^n-(1-P)^n**。
当P=0.5时,P(鞍点)=1-1/2^(n-1),当n趋近于无穷大时,P(鞍点)趋近于1,即此时该点肯定是鞍点。
在深度神经网络中,输入是高维的,存在很多鞍点的可能性很大,很难收敛到极小值;
但鞍点不是稳定点(不稳定即面对扰动,很容易跳出原始状态),使用SGD随机梯度下降法造成小扰动,可以逃离鞍点。
3.2.2悬崖问题
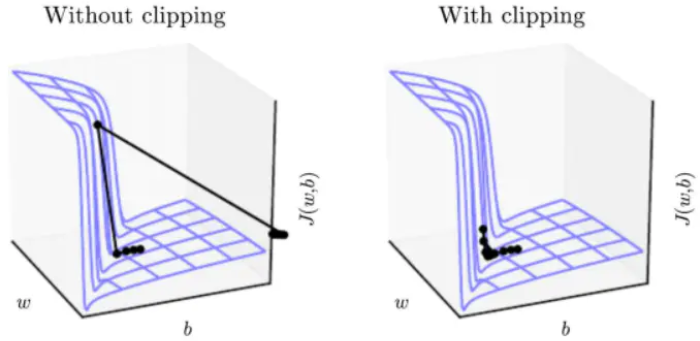
悬崖问题即像悬崖一样斜率较大的区域,在悬崖处更新梯度改变参数值,会由于导数较大而“飞出去”,会使参数弹射的非常远。悬崖结构是由梯度爆炸引起的。
悬崖结构在RNN的代价函数中很常见,例如:长期的时间序列会产生大量相乘。
可以用梯度截断(gradient clipping)解决悬崖问题,截断的思想是:通过干涉来减小步长,使得参数更新不可能走出很大一步,例如: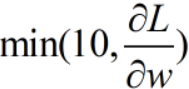 。
。
3.2.3峡谷问题
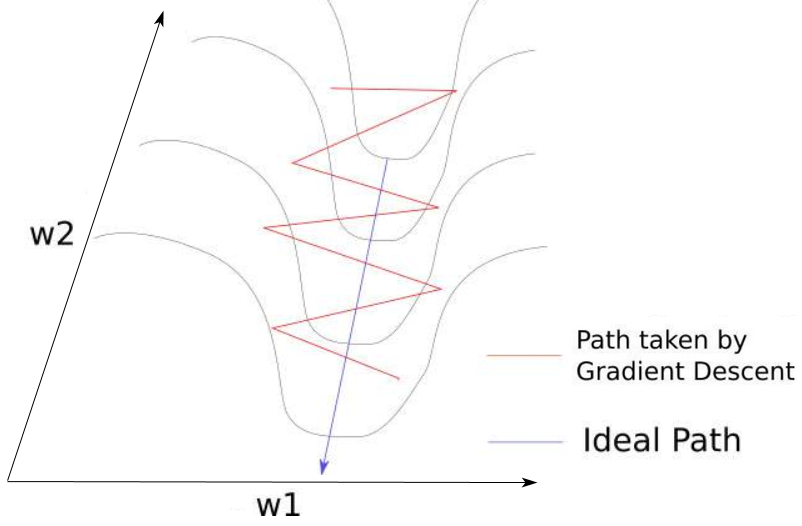
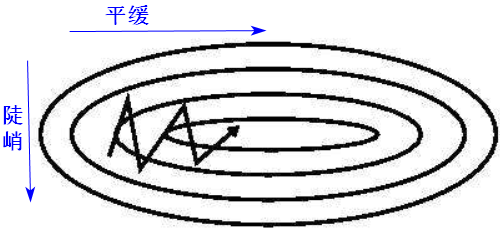
峡谷问题:在坡度平缓的地方,梯度小,下降的慢,期望下降的更快;在坡度陡峭的地方,梯度大,下降的快,期望下降的慢。
针对这个矛盾,陡峭意味着震荡,此时应该有较小的变化,在平缓处应该下降更快。
存在震荡的本质原因是各个方向(维度)上导数(梯度)的量级不一致。3.3优化方法
解决峡谷问题的方法:(所有算法具体参见“梯度下降”一文)
动量法(Momentum)+SGD:减小震荡
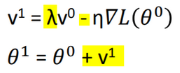 动量法,可以使梯度下降在梯度方向不变的维度上更新更快,在梯度方向有所改变的维度上更新变慢,可以加快收敛并减小震荡。
动量法,可以使梯度下降在梯度方向不变的维度上更新更快,在梯度方向有所改变的维度上更新变慢,可以加快收敛并减小震荡。
- Adagrad:统一各维度梯度的量级(归一化)
用r记录梯度量级,有: ,
, 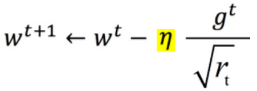 。
。
Adagrad的本质做了梯度量级的数值归一化,但随着r越来越大,后期梯度更新变慢。
- RMSProp:加权求和,解决量级越来越大的问题
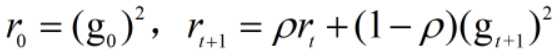
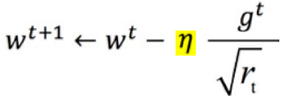
RMSProp对梯度进行了加权求和,只保留过去给定窗口大小的梯度,解决了Adagrad在后期梯度更新变慢的问题,加快了收敛。
也可以结合动量法+RMSProp。
- Adam:解决量级r和动量v初始化的问题
在Adagrad、RMSProp、Momentum中,动量v和量级r的初始化都为0。
Adam结合了RMSProp和Momentum的优点,m代表动量,v代表量级。随着更新次数n增大,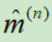 和
和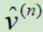 会越来越小,初始化时,放大了m和v。
会越来越小,初始化时,放大了m和v。
4.权重初始化
根据反向传播中求梯度的过程可知,权重W取值太大(梯度爆炸)或太小(梯度消失)都不合适。一般,W随机取值满足均匀分布,即均值为0,并控制方差。
4.1初始化原则一:打破对称性
如果神经网络中,某层两个神经元的w参数是一样的,即具有对称性,此时输入这两个神经元的信号是冗余的,因此需要打破对称性,一般考虑随机初始化。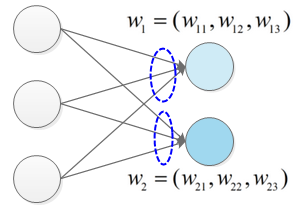
正交初始化
两个W向量正交时,两向量相互垂直,此时神经元接收到的信息没有冗余。
在n维空间,最多找到(n-1)个向量与已知向量正交;输入层有n个神经元时,则最多可以找到n个相互正交的向量,下一层神经元数量为m时(m>n),此时连接下一层神经元的m个W向量一定存在非正交的情况,但这种适当的冗余可以提高神经网络模型的稳定性。
正交初始化的弊端:寻找正交向量比较耗时,计算量大。
4.2初始化原则二:控制方差大小
如果W取值太小,则计算梯度时,可能导致梯度消失问题;
如果W取值太大,又可能导致梯度爆炸问题。
控制W的取值,就是控制W的方差σ,因此可以从方差入手去初始化W。
W取值与神经元数量

- W与上一层神经元数量的关系
当M神经元数量越多时,输出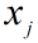 的数值越大,如果激活函数为sigmoid或tanh,导数趋近于0,输出接近饱和,梯度下降时,W参数将无法继续更新。此时,我们希望W取值小一些(方差σ也小,这样w随机出小数值的可能性更大),
的数值越大,如果激活函数为sigmoid或tanh,导数趋近于0,输出接近饱和,梯度下降时,W参数将无法继续更新。此时,我们希望W取值小一些(方差σ也小,这样w随机出小数值的可能性更大),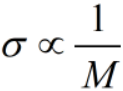 (成正比)。
(成正比)。
- W与本层神经元数量的关系
当本层神经元数量N越大时,导数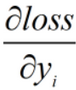 的数值越大。为了避免出现梯度爆炸,此时,我们希望W取值小一些(方差σ也小一些),
的数值越大。为了避免出现梯度爆炸,此时,我们希望W取值小一些(方差σ也小一些),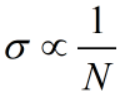 (成正比)。
(成正比)。
Glorot均匀分布初始化
W随机取值满足一下均匀分布(均值为0):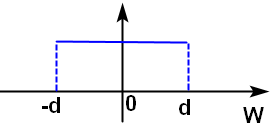 ,其中
,其中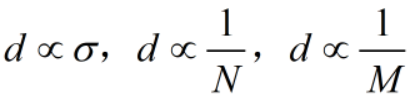 ,W初始化取值既和本层神经元个数N有关,也和上一层神经元个数M有关。
,W初始化取值既和本层神经元个数N有关,也和上一层神经元个数M有关。
当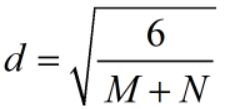 时,经实践证明[-d,d]是比较好的W初始化取值范围,这叫做Glorot均匀分布初始化,又称Xavier均匀初始化。
时,经实践证明[-d,d]是比较好的W初始化取值范围,这叫做Glorot均匀分布初始化,又称Xavier均匀初始化。
5.Batch Normalization
假设数据集中一共有R个样本,每个样本的特征维数一样,样本第i维的均值为,标准差为
,则对第r个样本的第i维特征做特征缩放(Feature scaling,例如:归一化)为:
。
5.1内部协变量偏移(internal covariate shift)
在DNN中,除了输入层的数据外,后面每一层的输入数据分布是一直在发生变化的(因为参数在更新),随着层层叠加,高层的输入分布变化会比较剧烈。每层输入的数据分布的不一致现象,叫做内部协变量偏移(ICS)。为了训练好的模型,就需要用尽量小的学习率、谨慎的初始化权重等,以减小偏移,但这会使得训练变慢。
随着网络层数的加深,输入分布经过多次线性非线性变换,已经被改变了,但是它对应的标签,如分类,还是一致的,即使条件概率一致,边缘概率不同。
机器学习中有个很重要的假设:IID独立同分布假设,就是假设训练数据和测试数据是满足相同分布的,这是模型能够在测试集获得好的效果的一个基本保障。当每个神经元的输入数据不再是“独立同分布”,导致了以下问题:
- 上层网络需要不断适应新的输入数据分布,降低学习速度(不得不采用更小的学习率)。
- 下层输入的变化可能趋向于变大或者变小,导致上层落入饱和区,使得学习过早停止。
- 每层的更新都会影响到其它层,因此每层的参数更新策略需要尽可能的谨慎。
解决ICS问题的思路是让输入分布满足独立同分布,有白化和归一化两种常用方式。
白化(Whitening)
白化是对输入数据分布进行变换,进而达到以下两个目的:
- 输入特征分布具有相同的均值与方差,其中PCA白化保证了所有特征分布均值为0,方差为1;而ZCA白化则保证了所有特征分布均值为0,方差相同;
- 去除特征之间的相关性。
通过白化操作,可以减缓ICS的问题,进而固定了每一层网络输入分布,加速网络训练过程的收敛。但是白化计算成本太高,每一轮训练中的每一层都需要做白化操作;同时白化改变了网络每一层的分布,导致网络层中数据的表达能力受限。
标准化(Normalization)
标准化就是将分布变换为均值方差一致的分布。改变了分布之后,输入x的取值范围不同了,因此标准化可以用来防止网络饱和(梯度消失问题),加速收敛过程。
在标准化公式中,均值是平移参数(shift),标准差
是缩放参数(scale),同时为了保证网络的非线性表达能力,加入
为再缩放参数(re-scale),
为再平移参数(re-shift)。
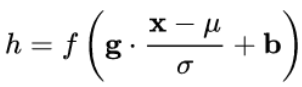
5.2标准化方法
BN,LN,IN,GN
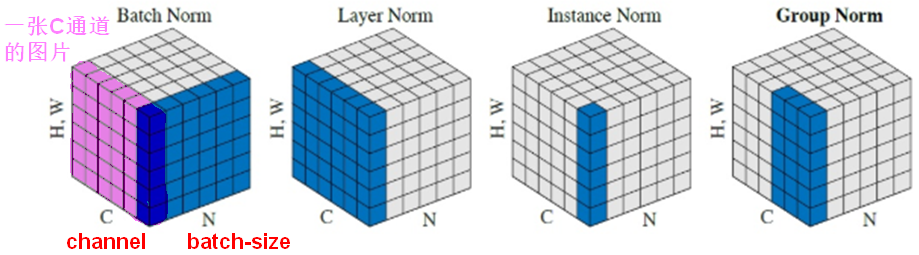
| 标准化 | 方式 | 使用场景 |
|---|---|---|
| BN | 对一个N批量的样本,分通道的计算均值和标准差。 | BN适用于固定深度的前向神经网络,不适用于RNN,因为批量中的通道数可能不一致;对较小的batch-size效果不好。 |
| LN | 单独对每个样本做归一化。 | LN对RNN效果明显。 |
| IN | 单独对每个样本分通道的进行归一化。 | IN用在风格化迁移。 |
| GN | 单独对每个样本进行channel分组,再针对每组进行归一化。 | GN适用于较小的batch-size。 |
5.3批归一化(BN)
在DNN中,对输入也可以做缩放。但网络的中间层是随着参数的更新而变动的,均值和方差不易统计。BN就是用来对各层做归一化的。BN在神经网络中使用的位置是全连接层或卷积操作之后,激活函数之前。
BN操作和算法
- 训练阶段的BN操作:
Batch Normalization将输出值强行做一次Gaussian Normalization和线性变换。做线性变换就是加入缩放变量γ和平移变量β,保证数据归一化后,还保留原有学习来的特征,加速训练;γ和β都是用来学习的参数。
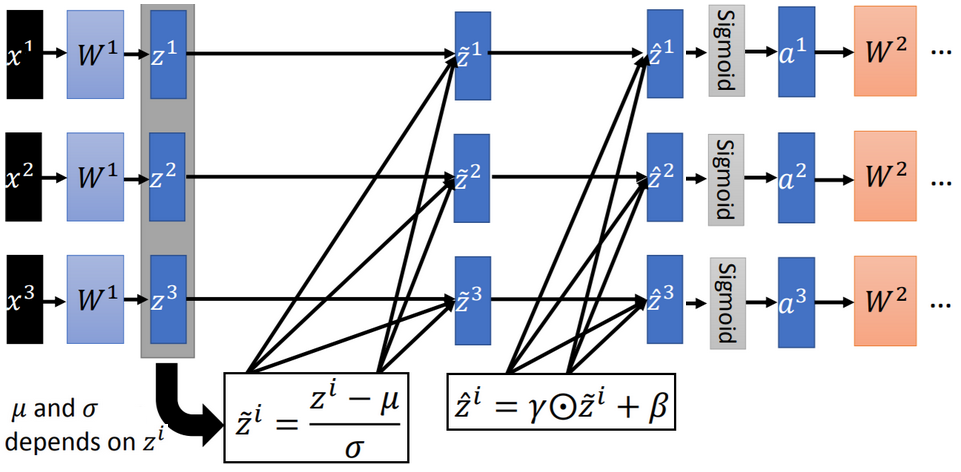

- 测试阶段的BN操作:
在测试阶段,由于没有批量数据(batch),所以就借助训练阶段每次更新的均值和标准差
,各自都取均值,或者为每次更新得到的均值和标准差附权重。

BN的优劣
【好处】:
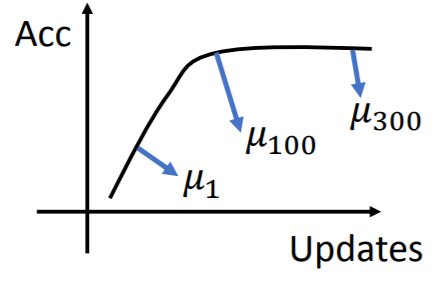
- 使用BN之后,可以减少深层网络的训练次数,训练更有效率。因为减少了内部协变量的偏移,可以使用更大的学习率,使得loss收敛更快;标准化之后,出现梯度消失/爆炸的可能性减小。
- 学习会更少的受到参数初始化的影响。参数的变化(K倍)会在标准化的过程中抵消掉。
- BN的作用也能替代对正则化的需求(相当于加入了噪声)。
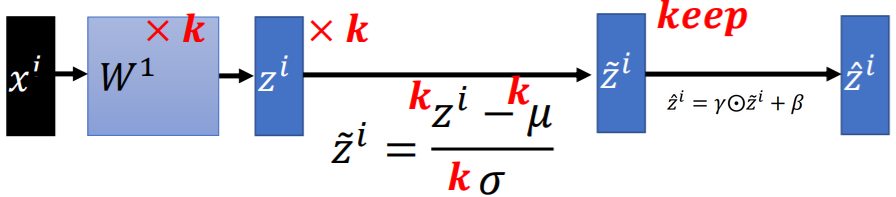
【坏处】:
- batch size太小:每次是在一个batch上计算的均值、方差不足以代表整个数据分布。
- batch size太大:会超过内存容量;需要跑更多的epoch,导致总训练时间变长;会直接固定梯度下降的方向,导致很难更新。

