数据预处理

1.正则化

正则化是加在损失函数之上，效果是牺牲了训练集内的正确率，而换取了验证集的正确率，目的是牺牲正确率来提高模型的推广能力。
L1正则化
L2正则化
（正则化部分详见“模型的泛化能力”）

2.特征缩放（Scaling）

【问题】为什么需要特征缩放？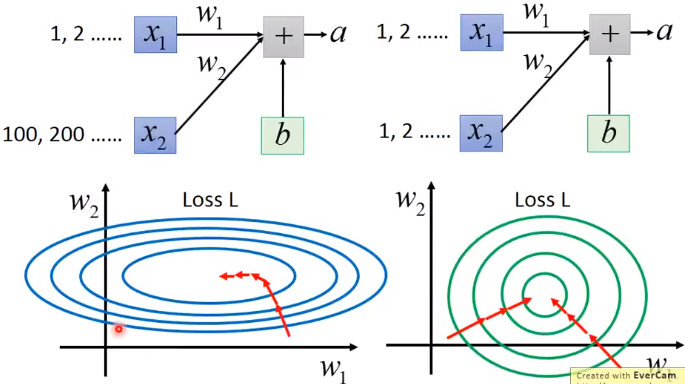

特征缩放，即让不同的特征的值保持同一量级，使得损失函数在收敛时更容易。

2.1归一化

同质性（homogenous）

所有特征的取值应该在大致相同的范围内，即具有同质性。
如果特征取值是异质的，会有什么影响？
异质的特征值会导致权重参数的变化对loss损失变化的影响有较大差异，可能导致较大的梯度更新，导致网络无法收敛；在神经网络中，对于sigmoid、tanh这样的函数，特征取值较大，会导致输出值趋于稳定，网络饱和，梯度不再更新和收敛。

最大值最小值归一化

标准归一化

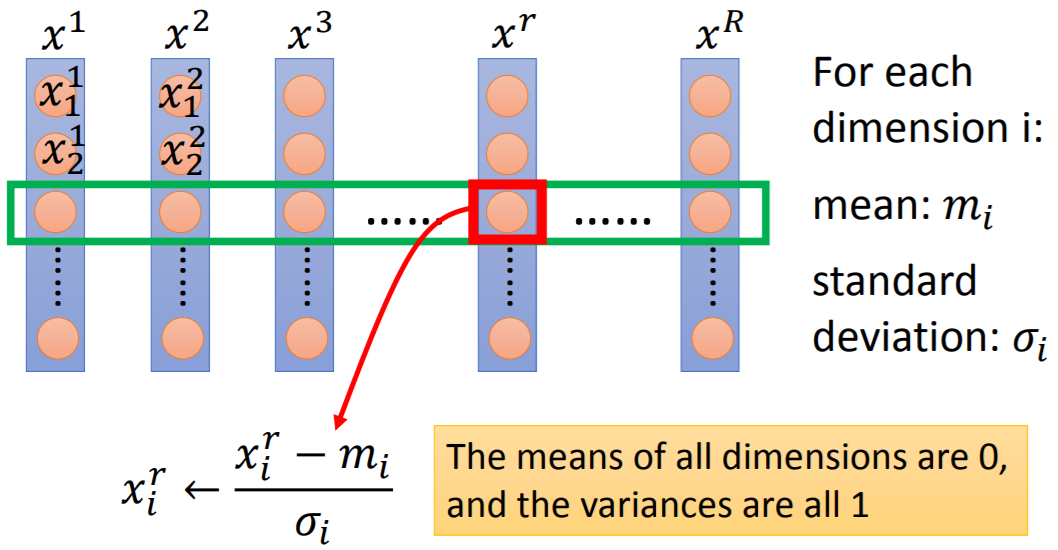
对样本某一维度的特征，求均值和标准差；做完均值方差归一化之后，该维度特征上的所有特征值均值为0，方差为1。
一般的，做完特征缩放（feature scaling）之后，梯度下降的收敛会更快。

3.特征转换（Transformation）

特征转换的方法比较灵活，并不是轻易的就能找到好的转换方式。

3.1.离散值VS连续值

如果离散属性间存在“序”order关系，可以连续化。例如：高、中、低可转化为{1.0,0.5,0.0}。
如果离散属性间不存在序关系，可以转化为n维向量。例如：男、女可转化为(1,0),(0,1)。

4.缺失值处理

• 缺失值填充

利用低秩矩阵进行特征值填充；
填充0.

• 删除有缺失值的特征

如果模型是在没有缺失值的数据上训练，测试数据中存在缺失值的这些特征也应该删除。