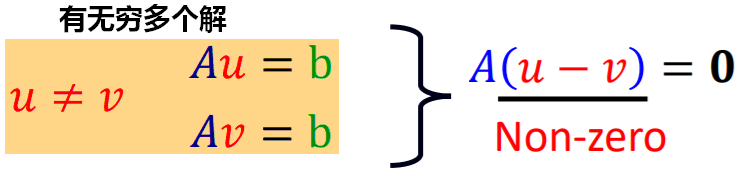一、线性系统

1.线性系统两大特性

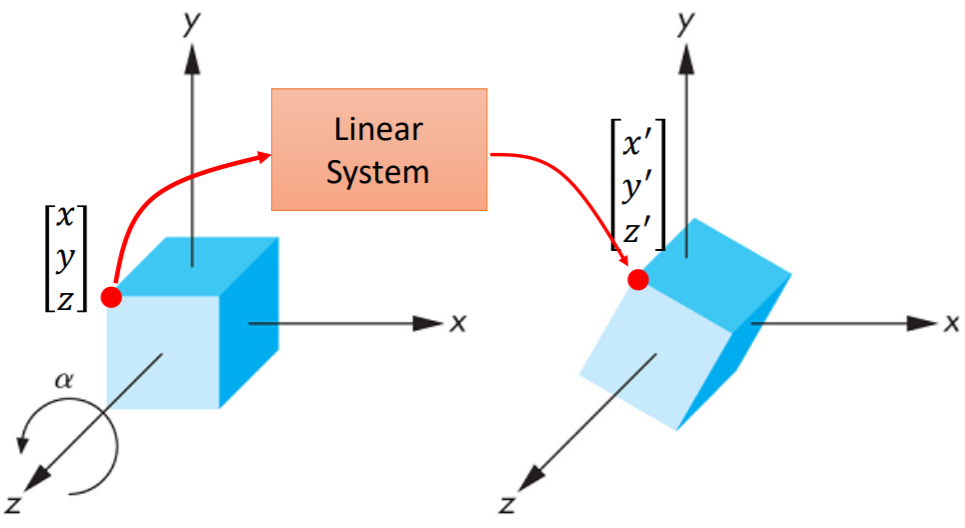
线性系统（Linear System）的输出值保留了输入值的乘法、加法计算，即输入乘以k，得到的输出是原始输出乘以k；输入相加，得到的输出是对应的原始输出相加。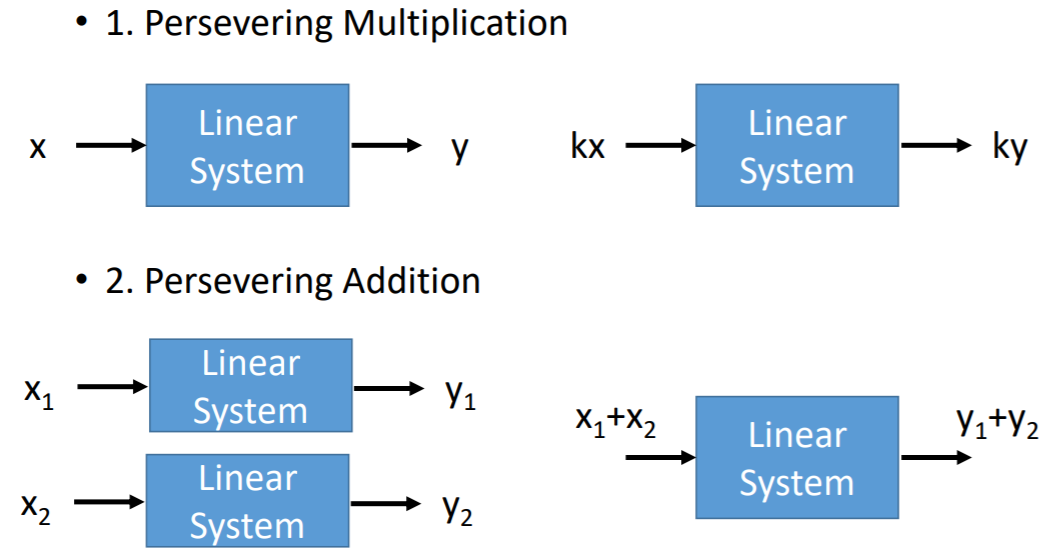
image.png

2.线性系统案例

非线性系统
image.png
以上系统不是线性系统，因为线性系统的两个特性都不满足。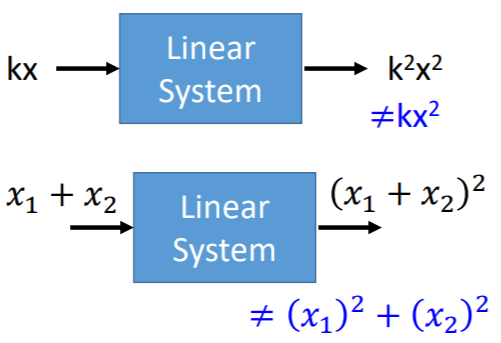
image.png
多输入的线性系统
image.png
这是一个多输入的线性系统，因为：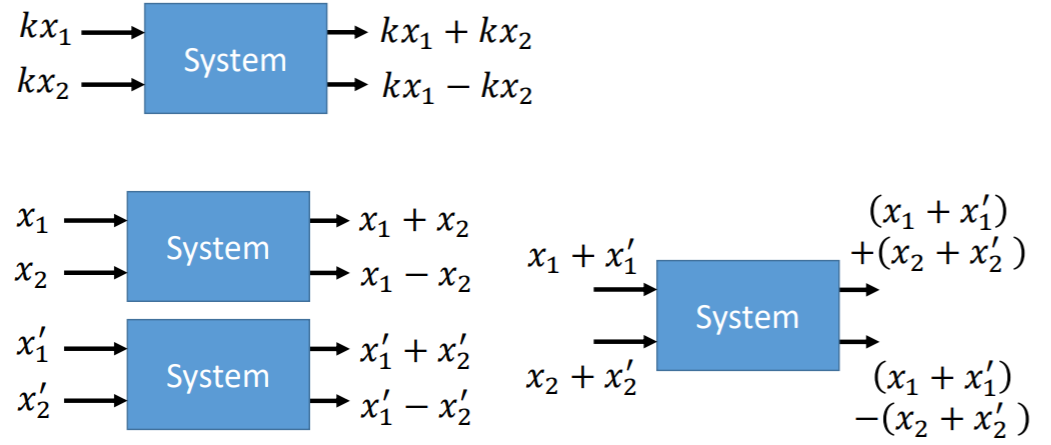
image.png
导函数
导函数也是一个线性系统：
image.png
积分
函数在某区间上的积分也是一个线性系统：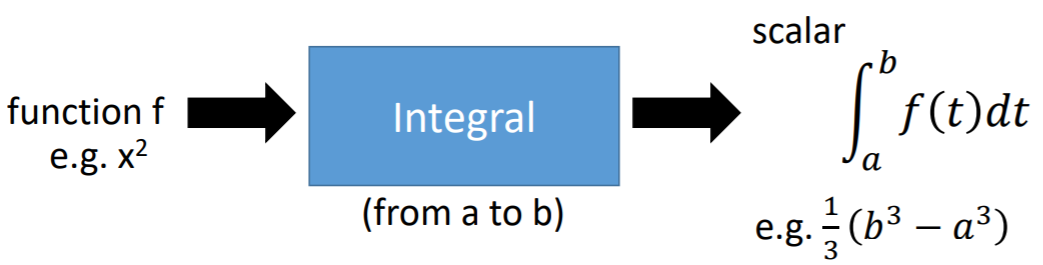
image.png

3.线性系统的应用

计算机图形学

空间中点（向量）的变换：
image.png

滤波器Filter

利用线性系统的特性，可以对输入进行放大或缩小。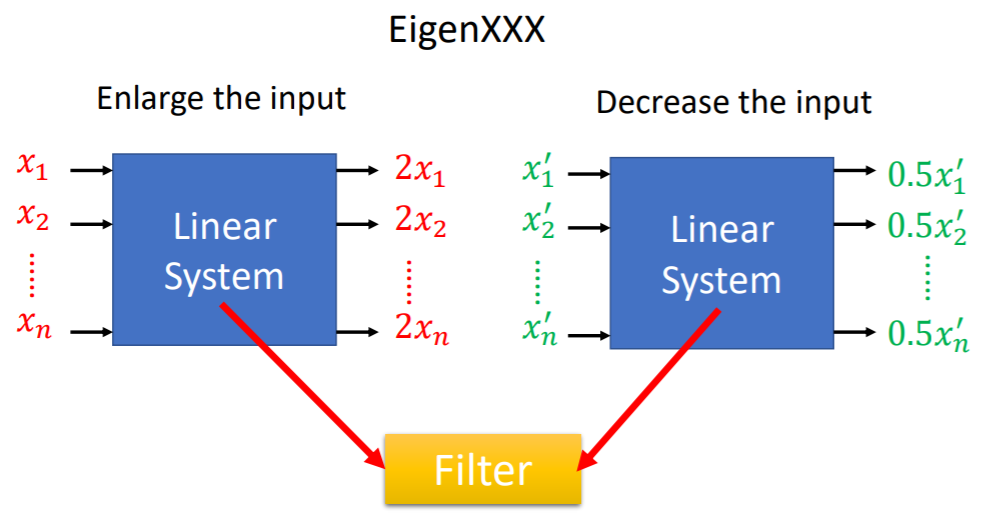
image.png

二、线性方程组

1.专业术语（Terminology）

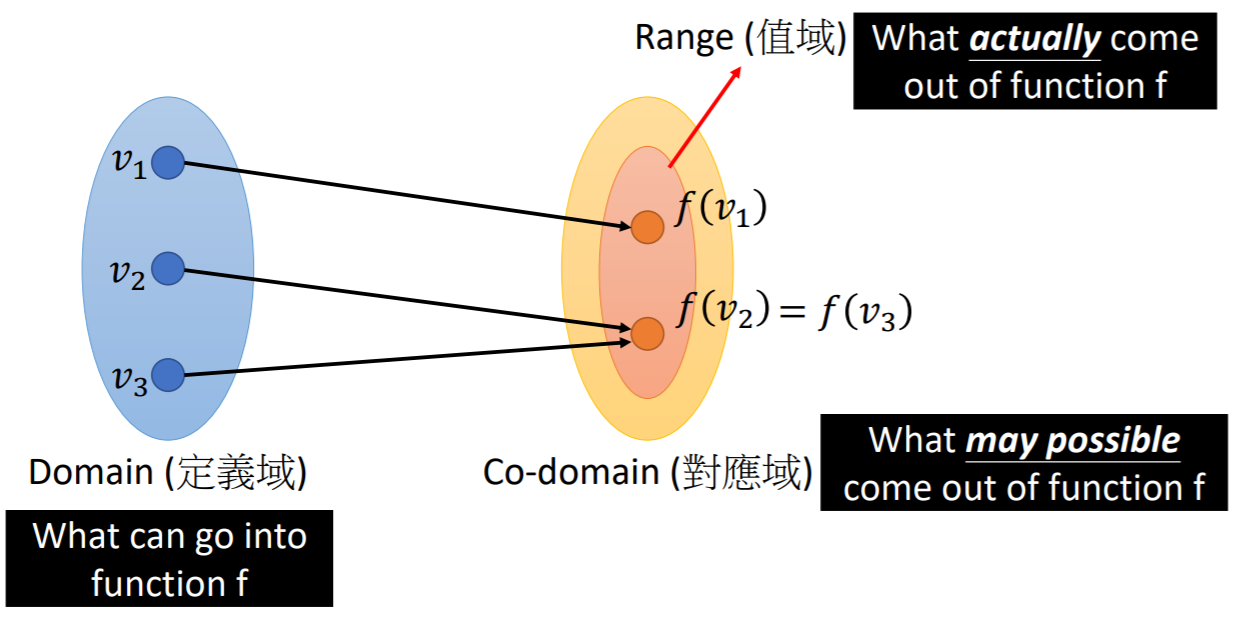
定义域、值域、对应域

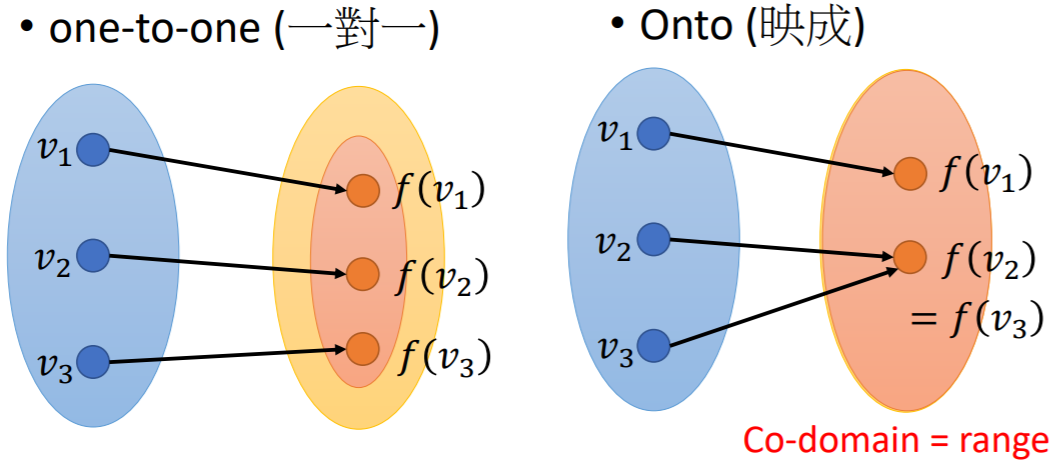
image.png

一对一、映成

image.png

2.多元一次方程组和线性系统

  • 多元一次方程组（System of Linear Equations）是一个线性系统：

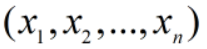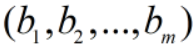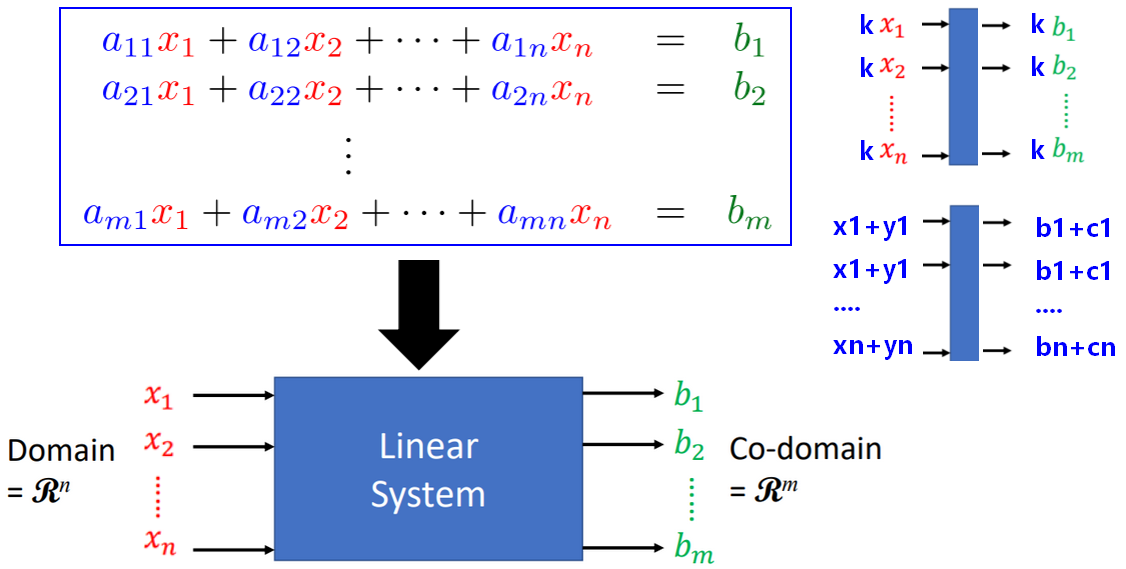
    它的输入为image.png，输出为image.png。
    image.png

  • 一个线性系统可以表示为一个多元一次方程组。

image.png

3.线性方程组的解

【问题】已知某个线性系统的输出，是否可以求出系统的输入？输入是唯一的吗？如何求解？
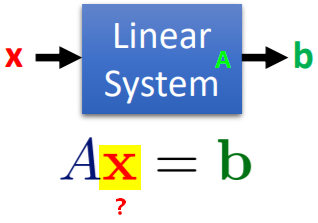
image.pngimage.png

相容/不相容（Consistent/Inconsistent）

image.png

线性组合（linear combination）

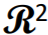image.png
【结论1】image.png中的向量，如果两个向量是不平行的，则线性组合一定有解（因为这两个向量可以表示二维空间中的任意一个向量。）反过来，如果有解，则这两个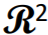image.png中的向量可能平行，可能不平行。
从向量角度理解线性组合：
image.png

Span,Space

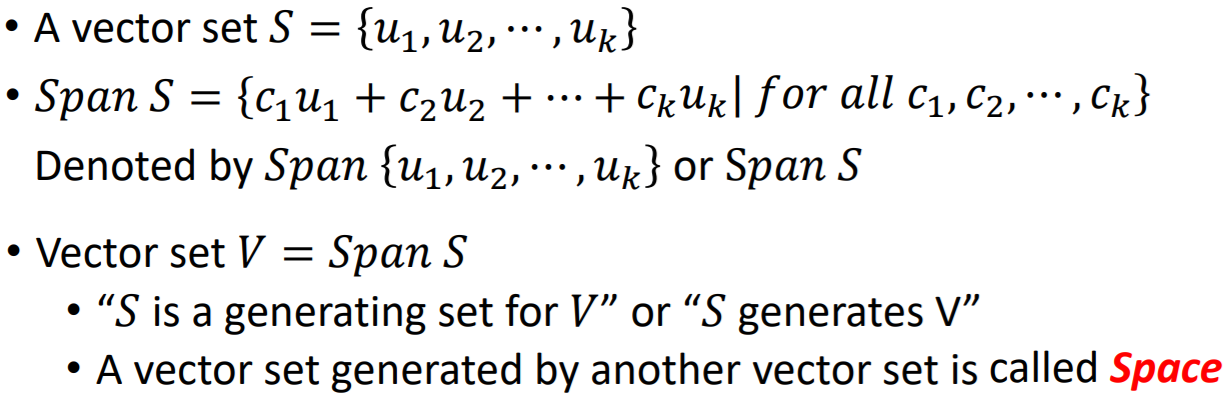
image.png
【结论2】不同数量的向量集合可以产生相同的Span，生成相同的Space：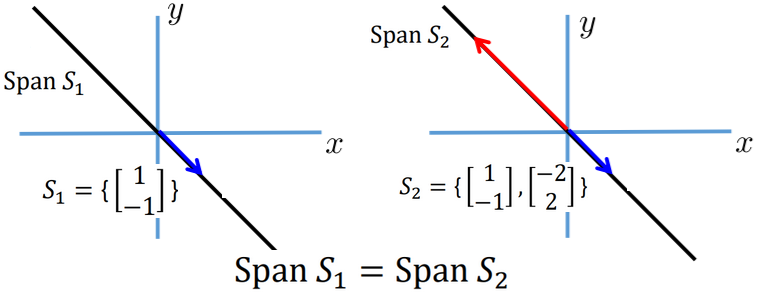
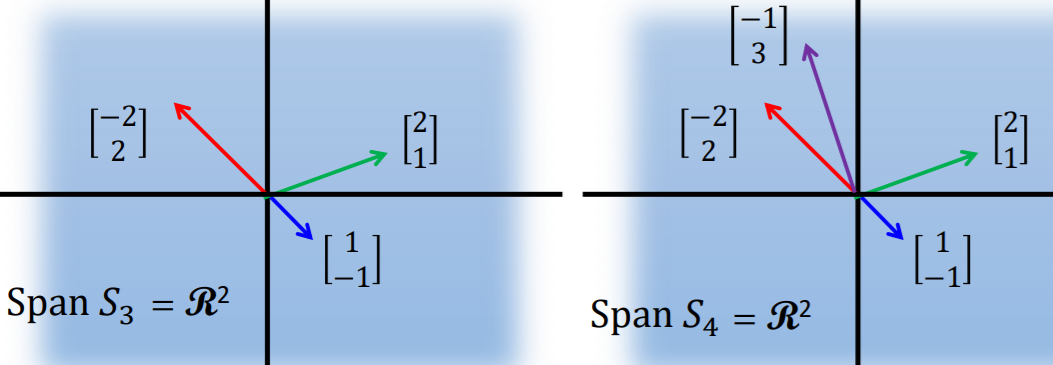
image.png
image.png
【问题转化】线性方程组有没有解？
>>> 该线性方程组是相容consistent，还是不相容inconsistent？（相容，则有解）
>>>> b是不是A的线性组合？（是，则有解）
>>>>>b是不是A在列方向上的向量的span？（是，则有解）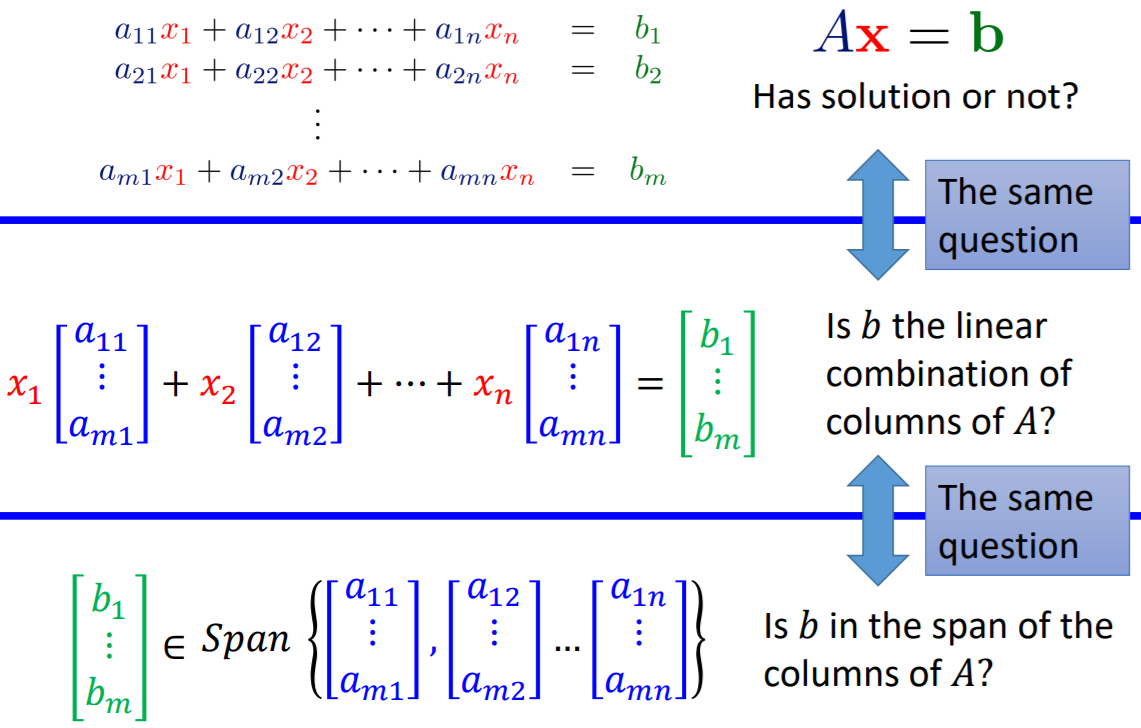
image.png

线性相关(Dependent)/无关(Independent)

对于向量集合(set)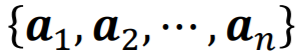image.png，
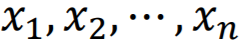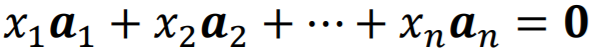如果存在不全为0的标量(scalar)image.png，使image.png，
则称这个向量集合线性相关(linear Dependent)。
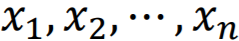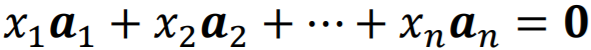如果当且仅当标量image.png全为0时，才有image.png，
则称这个向量集合线性无关(linear Independent)。
【结论】

  • 如果向量集合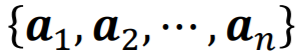image.png中存在一个向量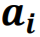image.png，它是其他向量的线性组合(linear combination)，则这个向量集合线性相关。
  • 如果向量集合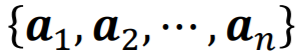image.png线性相关，则这个集合中存在一个向量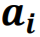image.png，它是其他向量的线性组合(linear combination)。
  • 任何一个向量集合中，只要有零向量，那这个向量集合就是线性相关的。

    秩(Rank)、零化度(nullity)

    对于一个矩阵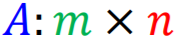image.png，
    矩阵的秩(Rank)：矩阵中线性无关(linear independent)的列(column)的最大数量。rank<=n
    零化度(nullity)：nullity = n - rank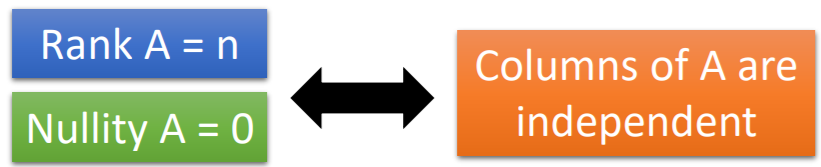
    image.png
    如果X是一个m x n的数值矩阵，rank(X)是X的秩，假如rank (X)远小于m和n，则我们称X是低秩矩阵(low-rank)。低秩矩阵每行或每列都可以用其他的行或列线性表出，可见它包含大量的冗余信息。利用这种冗余信息，可以对缺失数据进行恢复（低秩矩阵重构），也可以对数据进行特征提取（降维）。

    解的数量

    线性方程组（AX = b），如果有解，则要么有一个解，要么有无穷多解。
    一个矩阵A的列向量构成的向量集合是线性相关或无关，并不能直接推出线性方程组有没有解，只能得出如果有解时，解的数量。
    【结论】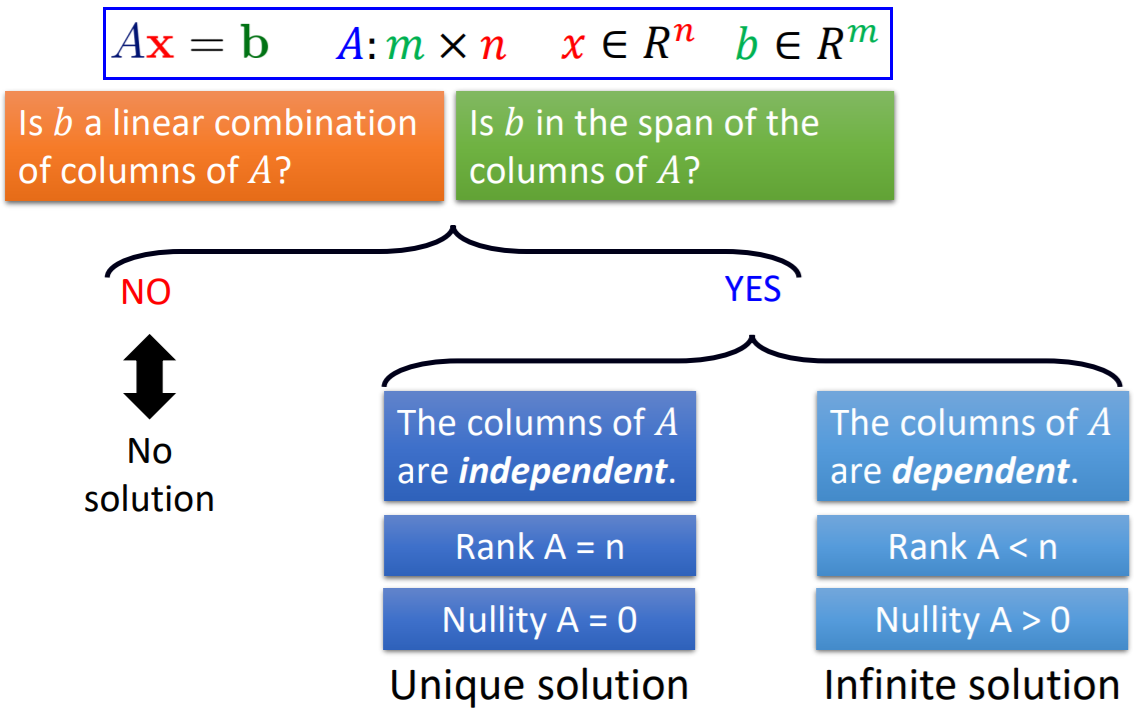
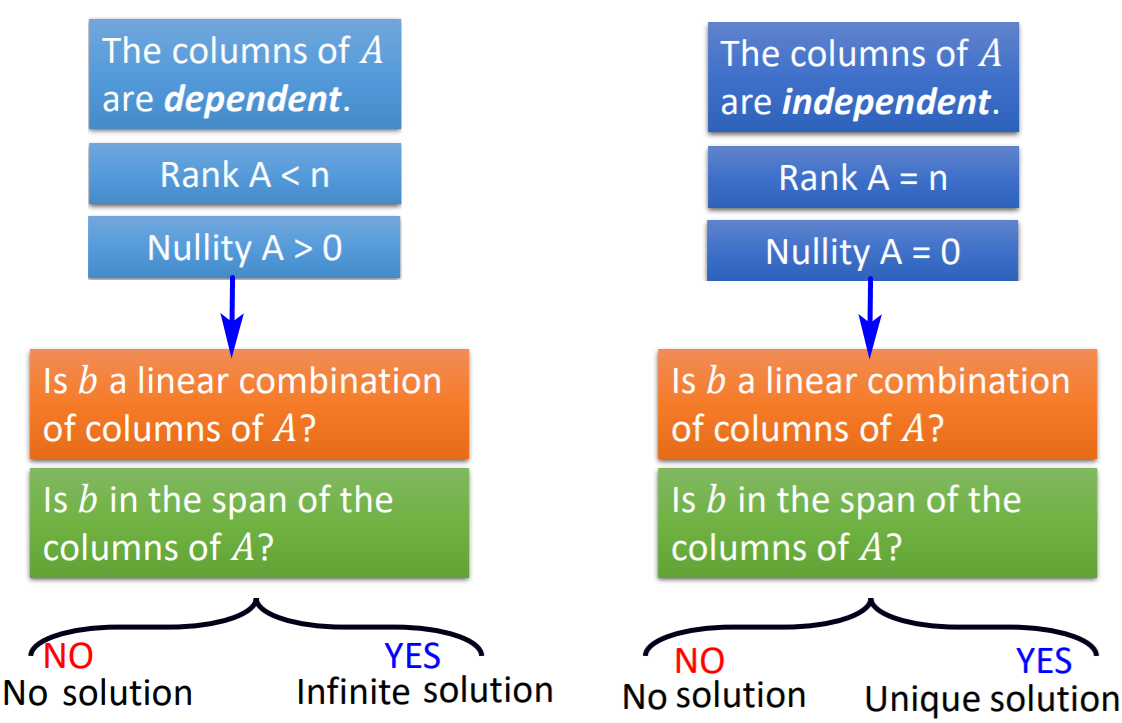
    image.png
    image.png
    【证明1：如果A的所有列向量线性相关，在线性方程组有解时，则 解有无穷多个。】
    image.png
    若三个向量在同一平面内——比如“列3”恰好等于“列1”加“列2”，而若b不在该平面内，则三个列向量无论怎么组合也得不到平面外的向量b。此时矩阵A为奇异阵或称不可逆矩阵。在矩阵A不可逆条件下，不是所有的b都能令方程_A_x=b有解。
    对n维情形则是，n个列向量如果相互独立——“线性无关”，则方程组有解。否则这n个列向量起不到n个的作用，其线性组合无法充满n维空间，方程组未必有解。
    【证明2：如果线性方程组有无穷多个解，则A的所有列向量线性相关。】
    image.png