1.Jensen不等式
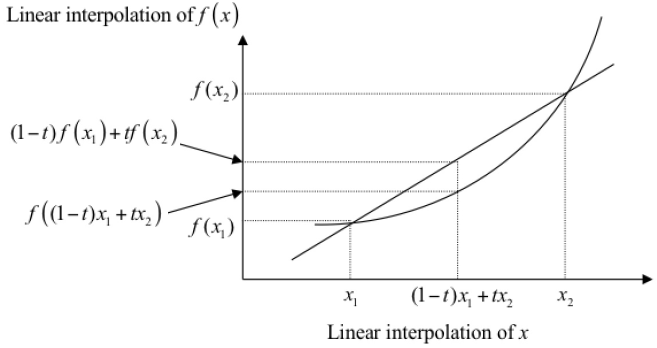
- 一般的,若
2.高斯分布(正态分布)
2.1高斯分布
估计分布的均值和标准差
假设有一组样本,来自于高斯分布
,估计
。
全部发生的概率为(相互独立、随机):
- 根据最大似然估计(MLE),当
取最大值时的
就是我们估计出的最合理的参数。
对以上似然公式取对数似然,
对求偏导,令导数为0,可得:
求得了均值和标准差,根据概率密度函数,就能计算出某个随机变量发生的概率。
2.2混合高斯分布
例如:男女身高各自符合高斯分布,但这两个分布的均值和方差都不同,是两个不同的分布
。
(可以设想观测数据这样产生:首先依据概率选择第k个高斯分布模型,然后依据第k个模型的概率分布生成观测数据,反映观测数据i来自第k个模型的数据是未知的,以隐变量γ表示。)
高斯混合分布中,“混合”并不是指有的随机变量属于分布1,有的随机变量属于分布2,而是某个随机变量是由K个高斯分布混合而来的(即分布之间是有叠加重合的)。
假设有一组样本,样本数量为N,分布的总数为K,取到各个分布的概率(先验概率)分别为:
,第k个高斯分布
的均值为
,标准差为
,概率密度为
。
对数似然
参考高斯分布的似然函数,结合全概率公式,GMM模型的似然函数取对数之后,得到对数似然:
这种形式不方便求导,使用EM算法,拆解为两步,总体目标是估计参数:。
估计分布来源:E-step
第i个数据由第k个分布形成的概率为(即第k个类别在生成这个数据时的贡献占比):
所有N个样本可以估计出个分布来源的概率。
(参数的区分:)
估计各个分布的参数:M-step
在分布k的贡献下,可以生成的样本点为
。在GMM中,每个分布都是高斯分布,对于每个分布,有:
GMM是EM算法的一个特例,可以计算出: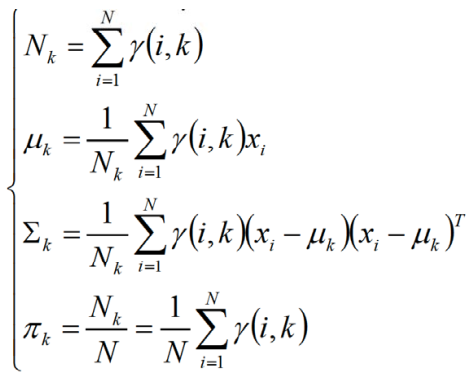 最终使用
最终使用来判别数据在各个分布上的概率。
GMM算法步骤
随机估计出参数值π,μ,σ,一共K组(对应K个分布,每个分布有三个参数值);
- 根据参数值π,μ,σ计算出γ(i,k),如果有N个样本,则一共要计算NK次*γ(i,k);
- 根据γ(i,k)的值,计算N*K个分量值(特征的分量值);
- 根据分量值,计算并更新参数值μ,σ,根据每组γ的比例更新π;
-
3.EM算法
EM算法(Expectatioin Maximization)即期望极大算法,是一种迭代算法,用于含有隐变量(hidden variable)的概率模型参数的极大似然估计,或极大后验概率估计。1977年由Dempster等人提出。
观测数据称为不完全数据(incomplete-data),观测数据和隐变量连在一起称为完全数据(complete-data)。 如果概率模型中不含隐变量,所有都是观测变量,就可以直接用MLE(或贝叶斯估计法)估计模型参数;
- 如果概率模型中含有隐变量,就使用EM算法来估计参数。
EM算法每次迭代分为两步:E-step,求期望;M-step,求极大。
3.1EM两步走
对数似然
假设样本数量为N,某个维度服从的分布为z(隐变量,很难直接找到参数估计),表示第i个样本所服从的某个分布,
为分布上的参数。则通过极大似然估计,得到对数似然为:
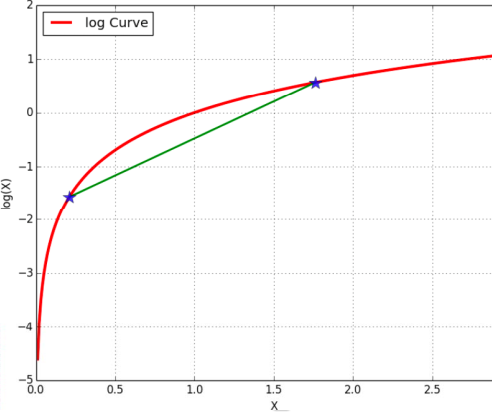
Jensen不等式
将看做
,将
看做参数,将
看做自变量,根据Jensen不等式,可得:
,且当自变量全部相等时,这个Jensen不等式取等号,所以可以将自变量看成一个常数构成的同一个点,即
。
E-step
根据Jensen不等式条件,有 ,
,
,
是样本由某个分布形成的概率,在混合高斯分布中,
。
M-step
3.2EM在GMM上的运用
一般混合模型中,可以由任意概率分布密度替代高斯分布密度。
在GMM中,参数为
,令
对均值和标准差求偏导可得:
对属于某个分布的概率求导,去掉常数项之后可得:
,
根据条件 ,构造拉格朗日函数:
求偏导:
EM算法推导GMM参数的对比

3.3EM算法的应用
- EM与K-Means
K-Means可以将未标记的样本标记为K类,但无法给出某样本属于某一类的后验概率,生成的类别标记相当于是一个稀疏向量;EM算法可以给出每个样本属于某个聚类的概率,生成的类别标记相当于是一个稠密向量。
- 图片前背景分离
前背景分离的实现是通过对像素进行分布的聚类。
- 声音性别检测

