1.贝叶斯网络
把一个系统中的所有随机变量,根据是否条件独立,绘制在一个有向无环图(DAG)中,就形成了贝叶斯网络,又称信念网络。贝叶斯网络是一种概率图模型。
1.1贝叶斯网络结构
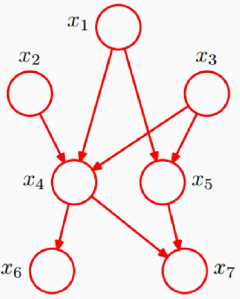
每个节点表示一个随机变量(可观察到的变量、隐变量或未知参数),连接的箭头表示两个节点之间存在因果关系(因:parents,果:children),两节点之间会产生一个条件概率值。
图中表示的联合分布概率:
如果没有贝叶斯网络,联合概率中的参数项会非常多。
一般的,对于有N个节点的贝叶斯网络,联合概率分布为:
1.2判断条件独立
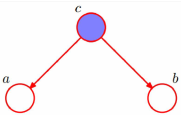
给定c的条件下,a和b是独立的。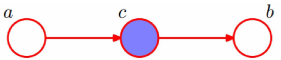
给定c的条件下,a和b是独立的。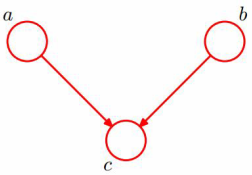
当且仅当c未知的条件下,a和b是独立的。
1.3马尔科夫链
的状态只和
有关,和其他变量条件独立,这种随机过程叫马尔科夫链(Markov chain)。
每一个节点的可取值范围是一样的。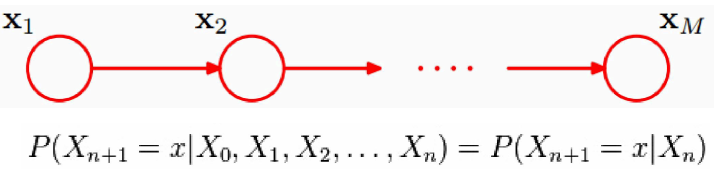
2.隐马尔科夫模型(HMM)
隐马尔科夫模型是关于时序的概率模型(生成式模型)。
HMM描述了这样一个过程:由一个隐藏的马尔科夫链随机生成不可观测的状态随机序列(state sequence),再由各个状态生成一个可观测产生的观测随机序列(observation sequence),序列的每一个位置都可以看做一个时刻。
HMM的应用有:词性标注(Tagging)、语音识别(Speech Recognition)等。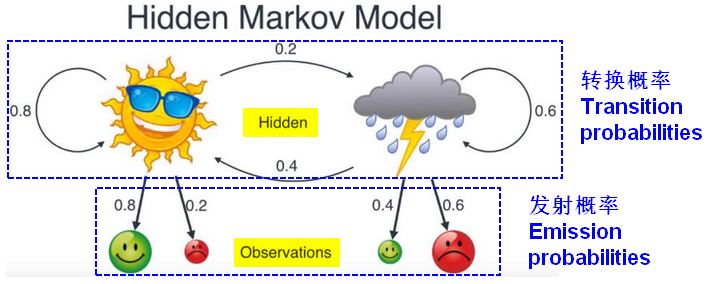
2.1HMM联合概率分布
2.2模型组成的三要素
初始概率分布
状态转移概率分布
观测概率分布三元组就定义了一个隐马尔科夫模型。
Q:所有可能状态的集合,一共N种可能状态,
S:长度为T的状态序列,
A:状态转移概率矩阵(NN),表示时刻t处于状态
的条件下,在时刻(t+1)转移到状态
的概率。
表示在*(t=1)的初始时刻,处于状态
的概率。
V:所有可能观测的集合,一共M种可能观测,
O:状态对应的长度为T的观测序列,
B:观测概率矩阵(N*M),表示时刻t处于状态
的条件下,生成观测
的概率。
模型的基本假设
齐次马尔科夫性假设:隐马尔科夫链时刻t的状态只和(t-1)的状态有关。
观测独立性假设:观测只和当前时刻状态有关。
2.3观测序列的生成过程
输入:隐马尔科夫模型
,观测序列长度为T;
输出:观测序列按照初始状态分布π,产生状态
,t=1;
- 按照状态
的观测概率分布,生成观测
;
- 按照状态
的状态转移概率分布,产生状态
;
令t=t+1,如果t
初始状态的概率
初始状态的概率是一个先验概率,可以根据数据分布中的频率估计,也可以结合转换概率去计算。
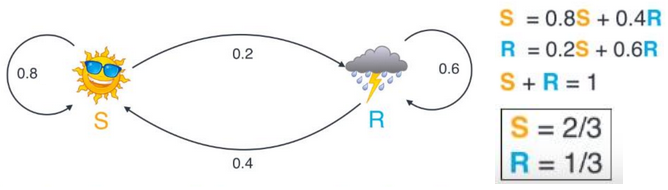
2.4模型的三个基本问题
观测序列概率计算问题:
(评估模型与观测序列之间的匹配程度)
已知:
求解:
【算法】:前向算法、后向算法。学习问题:
(训练模型,找到可以更好的描述观测数据的模型参数。)
已知:
求解:估计,使得
最大。
【算法】:监督学习算法:训练数据包括观测序列和状态序列。可使用极大似然估计法来估计HMM参数。
非监督学习算法:训练数据只包括观测序列。使用Baum-Welch算法。
预测问题/解码问题:
(根据观测序列,推断出隐藏的状态序列。)
已知:
求解:有最大概率时的状态序列
【算法】:近似算法、维特比算法。2.5Viterbi算法:动态规划
已知两天的心情
 ,推测最有可能的天气情况,分以下四种情况:
,推测最有可能的天气情况,分以下四种情况:
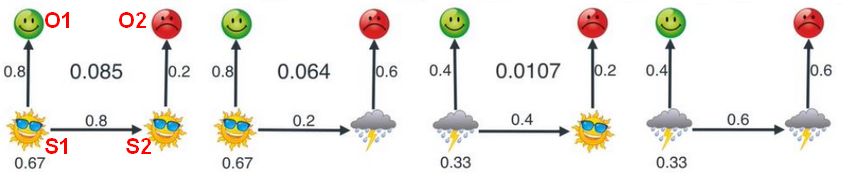
计算联合概率:
- 已知三天的心情,推测最有可能的天气情况,其中之一如下:
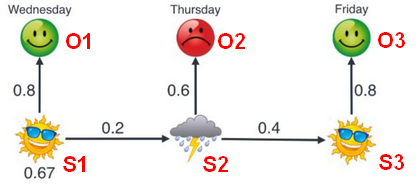
计算联合概率:
已知六天的心情,推测最有可能的天气情况:
每个时刻都有两种天气选择(晴天/雨天),可能的路径一共有
种,暴力穷举并不明智。维特比(Viterbi)算法是一种最近路径规划算法,从后往前计算出各种情形来比较,每次正向计算只保留最大的概率,最后得出最佳路径。
例如:
星期一是晴天的概率:
星期一是雨天的概率:
星期二是晴天的概率:
(保留最大的概率0.341)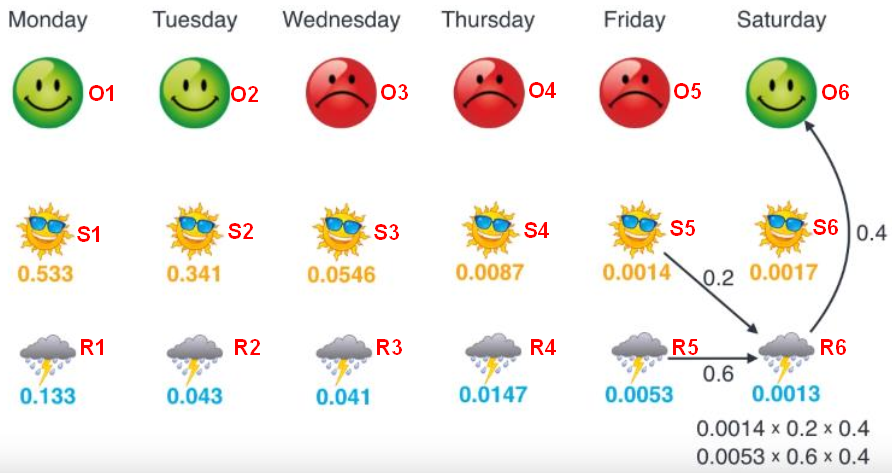
来源: 1.清华大学公开课;袁春 博士生导师
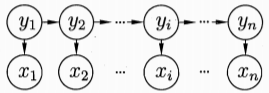 ,所有变量的联合概率分布为:
,所有变量的联合概率分布为:
