模型 - 模型的泛化能力 - 《机器学习》

1.模型误差error
2.正则化 Regularization
2.Dropout
3.剪枝

1.模型误差error

1.1 学习目标

误差分为：
【经验误差】empirical error：模型在训练集上的误差。
【泛化误差】generalization error：模型在新样本上的误差。
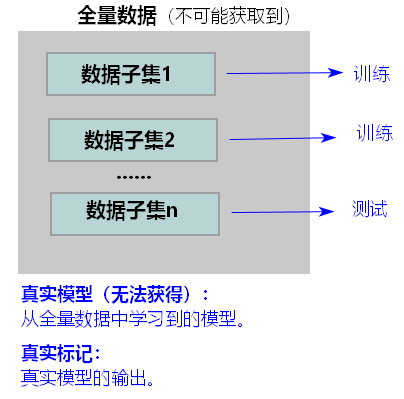
训练一个模型的最终目的，不仅让模型在训练数据上表现得好，在测试数据上同样表现得好，因此需要减小泛化误差。总体上，思路有两个：

减小经验误差。
使经验误差和泛化误差尽可能相等。

具体来说，方法有：

【调整数据】增大训练集的数量。例如：深度学习中的数据增强（augmentation）。
【调整数据】增加训练集的多样性，使之更好的代表整体数据。
【调整数据】使用验证集，在训练中验证模型的泛化能力。
【调整模型】挖掘更多的（隐藏）特征，或使用组合特征。
【调整模型】审视学习算法的假设是否正确，调整模型的复杂度。
【调整模型】加入正则化，避免过拟合。（L1,L2,dropout）

1.2 误差的来源
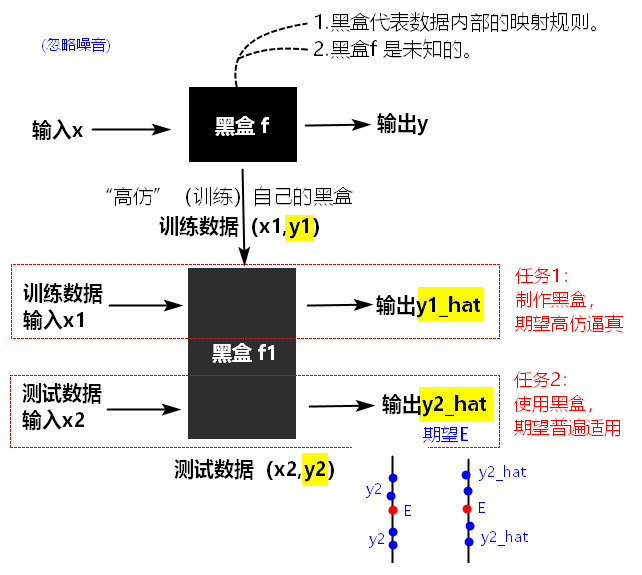
假设最理想/真实的模型为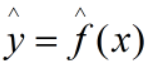：，我们根据training data训练得到的模型为：。
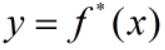是对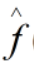的估计（Estimate），二者之间的距离，就造成了误差Error。
【理解】训练的模型，不管训练集多大，不管如何调优，一定存在误差。因为训练集终究只是全量数据的一个子集，在不同的训练集上会产生参数不一样的模型。首先，众多模型和期望值之间存在方差；其次，模型输出和“真实模型”输出之间也存在偏差。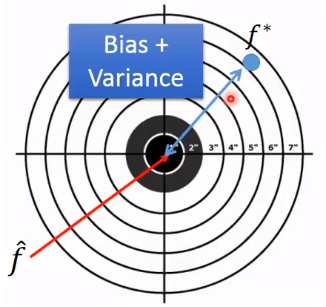

偏差bias：准确性
训练后所得模型的偏差：
度量了期望输出与真实标记之间的偏离程度；表达了模型本身的拟合能力。
（期望输出即所有预测值的平均值）

【问题】偏差产生的原因？
偏差引起的误差在经验误差上就能体现。偏差产生的原因包括：
对学习算法做了错误的假设。
模型的复杂度不够。（但是复杂模型又容易过拟合，导致方差variance变大，所以需要trade-off）

方差variance：稳定性
训练后所得模型的方差：
度量了数据扰动（当数据集变动时）所造成的模型学习性能的变化，反映模型预测的偏离与波动程度。

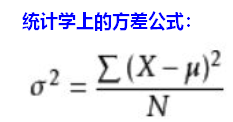
【问题】方差产生的原因？
方差引起的误差通常体现在泛化误差相对于经验误差的增量上。方差产生的原因包括：
模型过拟合

噪声：学习难度
噪声反映了学习问题本身的难度，表达了模型能达到的期望泛化误差的下界。

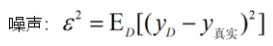
泛化能力：Trade-off

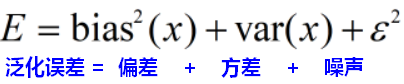
模型的泛化能力由学习算法的能力（偏差）、数据的充分性（方差）、学习任务本身的难度（噪声）共同决定。
训练初期，模型的拟合能力差，预测不准，所以泛化误差大，偏差bias也大；训练数据集还没有来得及对模型产生影响，此时将模型应用于不同的数据集（分布相同）也不会有太大差异，所以方差variance较小。
训练加深后，模型拟合能力变强，预测渐准，所以泛化误差减小，偏差bias也减小；但此时，训练数据的噪音和扰动渐渐被模型学到了，当预测新的数据集时，结果的波动较大，所以方差variance变大。
训练充足后，模型的拟合能力非常强，偏差bias更小了，学到了非全局的特征，预测效果变差，发生过拟合，泛化误差开始增大；数据变动会导致学习器发生显著变化，方差variance变大。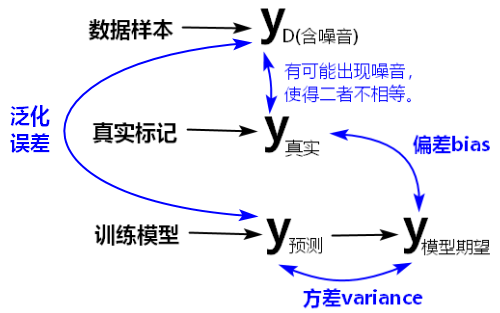

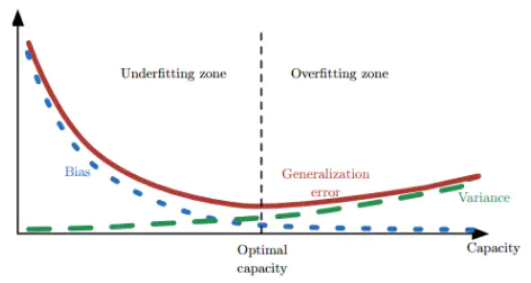
【问题1】什么会影响两个函数之间的距离？
偏差Bias和方差Variance会影响两个函数之间的距离。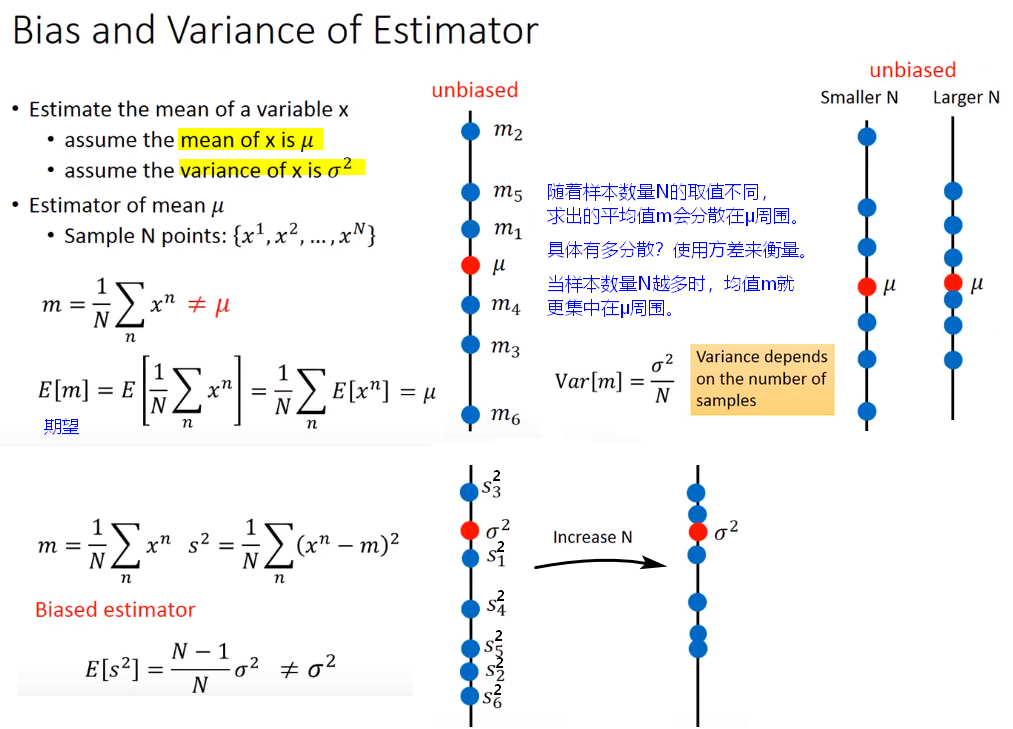

1.3 损失的优化目标

结构风险+经验风险

1.4 过拟合overfitting

过拟合是通常是机器学习中算法表现不佳的主要原因。
奥卡姆剃刀定律（Occam’s Razor）：如无必要，勿增实体；在其他条件一样的情况下，选择较不复杂的假设。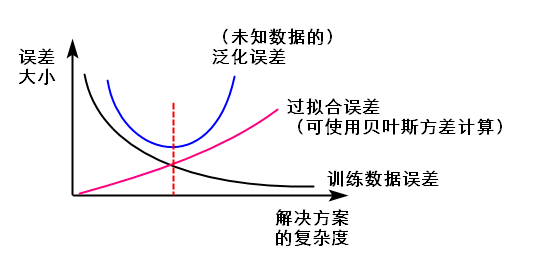

当假设越来越复杂（即模型更复杂）时，训练数据误差error小了，更拟合数据了，但会出现过拟合情况，泛化误差和过拟合误差大，泛化能力弱；
选择复杂度较低的模型，反而可以获得较好的泛化能力。

过拟合表现实例

【例如】当线性模型越来越复杂时，虽然训练集上的MSE不断减小，即模型拟合了训练集数据；但测试集上的MSE却有先减小再增大的趋势。

如何解决过拟合问题？

过拟合，即经验误差过于小，导致泛化误差变大。
我们的目标是让模型在没有见过的数据上表现得好。为了避免过拟合问题，可以：

在损失函数中加入正则化（惩罚项），以便获得更好的模型参数。
避免使用过于复杂的模型（假设空间），（在深度学习中）减小网络大小，例如：层数和神经元个数。（奥卡姆剃刀）
early stopping，使用验证集，避免过度学习。

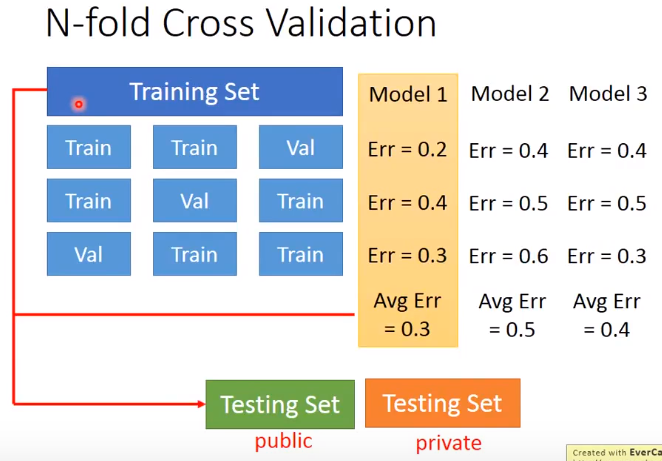
2.正则化 Regularization

在线性模型用于回归的任务中，
当特征值增多，模型变复杂后，出现了过拟合（overfitting）和泛化能力变差的现象。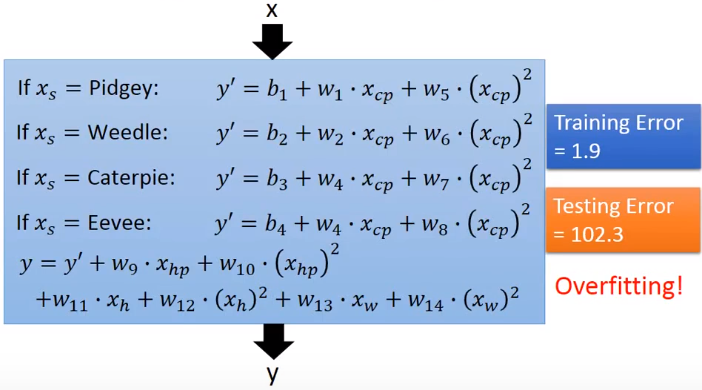

为了减小误差Error，我们重新定义损失函数，加入惩罚项，约束参数W，即对于输入参数w，我们希望越小越好。这样，使loss function既考虑误差大小，也考虑函数的平滑度（由**参数W大小决定**）。
【注意】由于惩罚项只在训练时添加，所以模型的训练损失可能会比测试损失要大。

【问题1】为什么参数W越小越好？

答：这样function可以更平滑（Smooth Function: 即output对input的输入更加不敏感）。
对于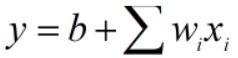，当输入有变化时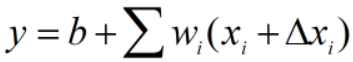：，输出的变化为：，
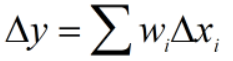即参数W越小，输入的变化对输出造成的影响越小。

【问题2】为什么正则化中不考虑偏置项bias？

答：因为bias对function的平滑程度没有影响。

【问题3】为什么需要一个更平滑的function？

答：输入中可能是带有噪声的，而平滑意味着output对input的输入更加不敏感，抗干扰/噪声能力更强，在测试集Testing Data上的结果会更好。
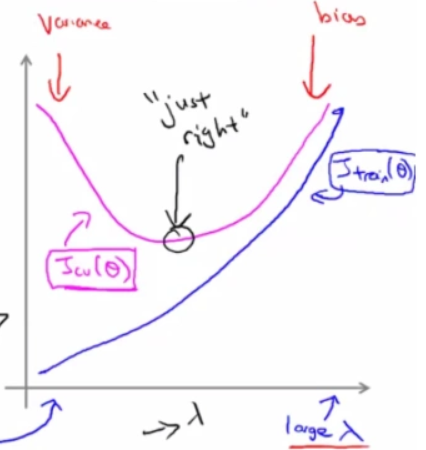
当 λ 值越来越大时，表示更看重Loss损失函数中的平滑度因素，更不看重误差Error，所以训练集上的Loss越来越大；当 λ 值越来越大时，函数越平滑，抗干扰能力更强，所以测试集上的Loss会先变小；但函数太过平滑也不是所需要的，预测能力会变差，所以测试集上的Loss会再变大。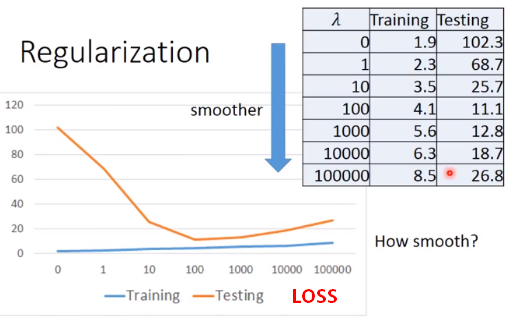

【问题4】怎么样获取理想的平滑度？

调整 λ 以便获得理想的平滑度，例如上例中，λ=100时，预测效果较好，此时的平滑度较为理想。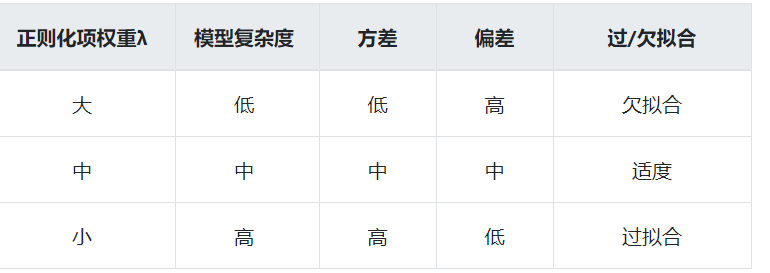

L1正则

模型的泛化能力 - 图28 范数（norm）是常用的正则化项：模型的泛化能力 - 图30
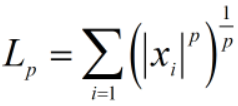
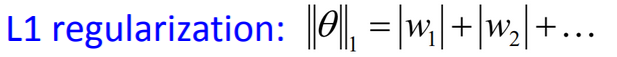
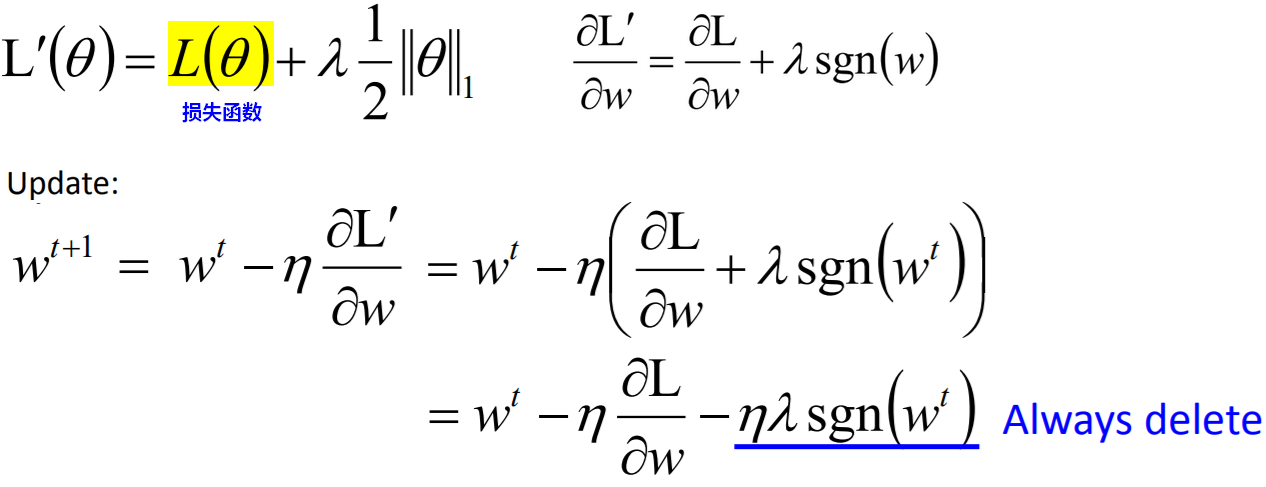
当p=1时，为L1正则：模型的泛化能力 - 图32

当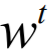是正数时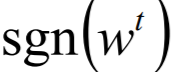，为1，且不管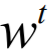多大，更新都是减去一个较小的数；
当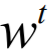是负数时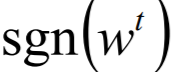，为-1，且不管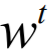多大，更新都是加上一个较小的数。
【结论】

在损失函数优化中加入L1正则，因为加/减相同的数值，会让参数W之间数值差异较大，有的W为0/趋近于0，有的W数值较大。整体上W向量会较为稀疏（sparse）。
会牺牲最不重要的维度（对应的w变为0），起到降维的作用，可以用来做特征选择。实际中是用L1较多。
L2正则
，当p=2时，得到L2正则：

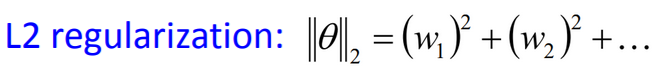
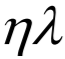本身是一个较小的值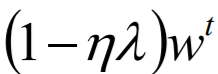，会让参数W越来越接近0（不管W本身是正是负），这就是权重衰减（decay）。
【结论】在损失函数优化中加入L2正则，会使权重衰减，参数W向量的元素平均的变小。