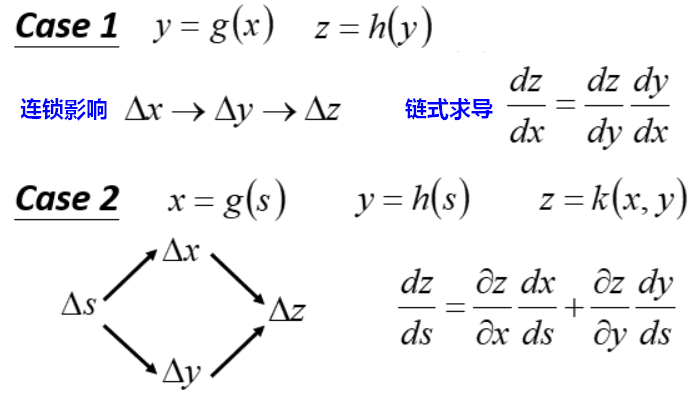1.深度学习简介

1.1发展历史

image.png

1.2 神经网络概念

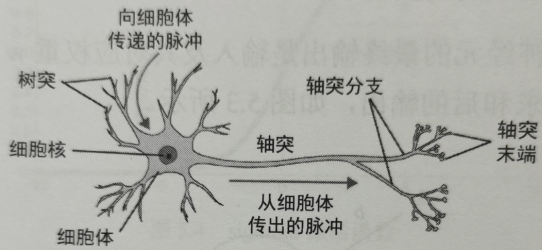
image.png image.png

神经元

神经网络中的基本计算单元，也叫节点/单元。

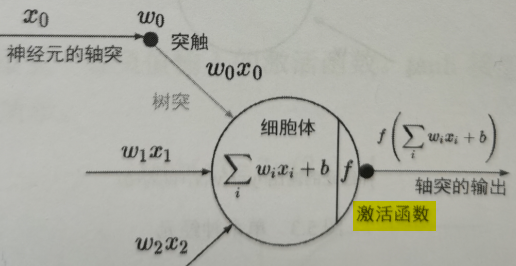
激活函数

树突将信号传到细胞体（神经元），信号相加的结果高于某个阈值，则激活神经元。激活函数将神经元输出变为非线性的表示方式，并将输出压缩到特定范围内。

2.深度学习三步走

image.png

  • 模型：设计神经网络的结构，定义了网络结构，即定义了假设空间（函数集），参数待定。
  • 策略：确定损失Loss，通过最小化损失进行模型评估。
  • 算法：选择最优函数

    2.1设计神经网络

    全连接前馈神经网络

    前馈（feedforward）：即前向，信号进入网络后，任意两层之间只有信号的单向流动，没有反向的反馈（feedback）。
    全连接（fully connnect）：前一层和后一层的神经元两两之间都有连接。
    深度（Deep）：有多个隐藏层。
    隐藏层（Hidden Layers）：通过隐藏层做特征转换（transformation），通过特征提取（extractor）来替代原来的特征工程（feature engineering）。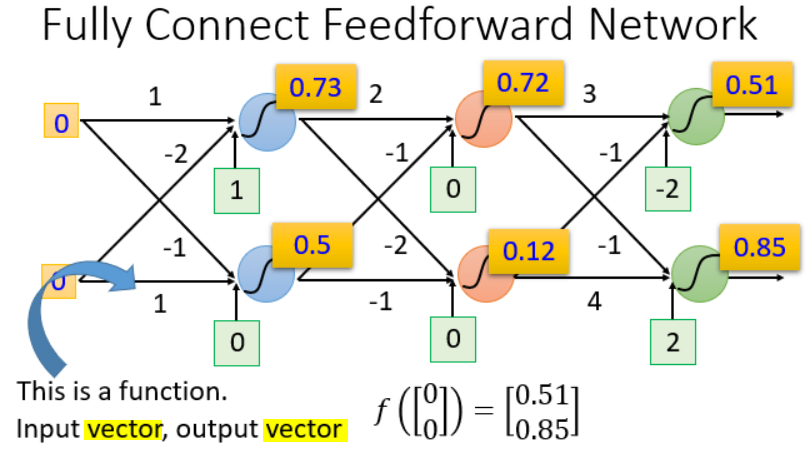
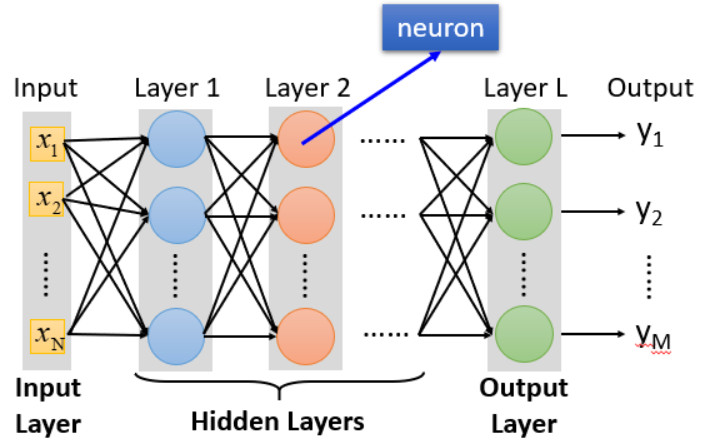
    image.pngimage.png
    神经网络的结构决定了假设空间的函数集，隐藏层和输出层部分就包括了我们定义的函数集，我们要从中通过调整参数，选择一个最好的函数。

    矩阵运算

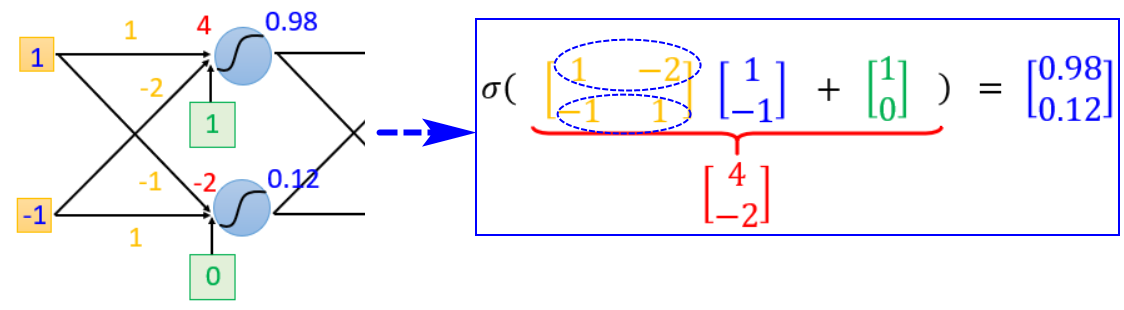
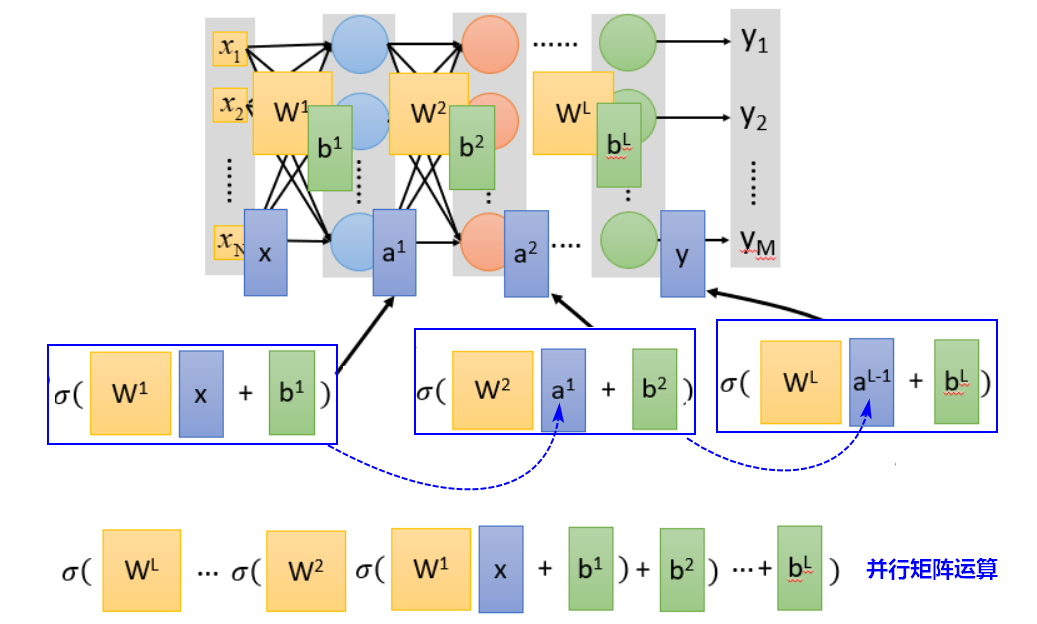
    image.png
    image.png

2.2模型评估

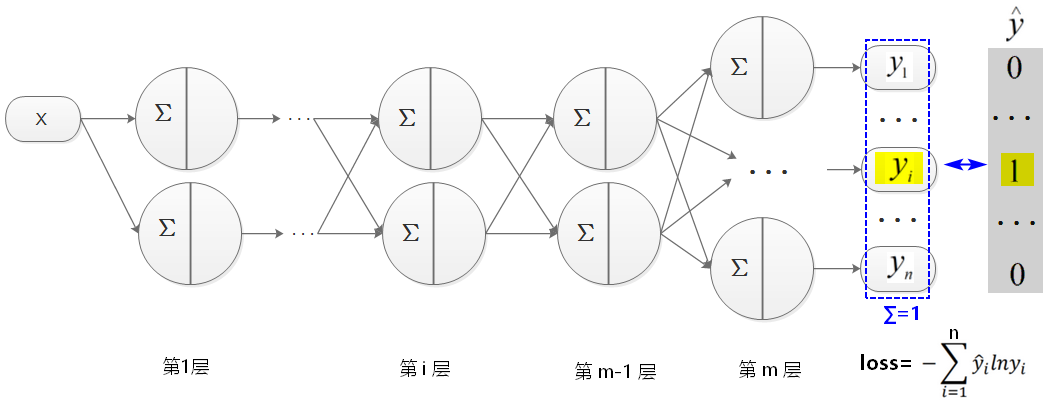
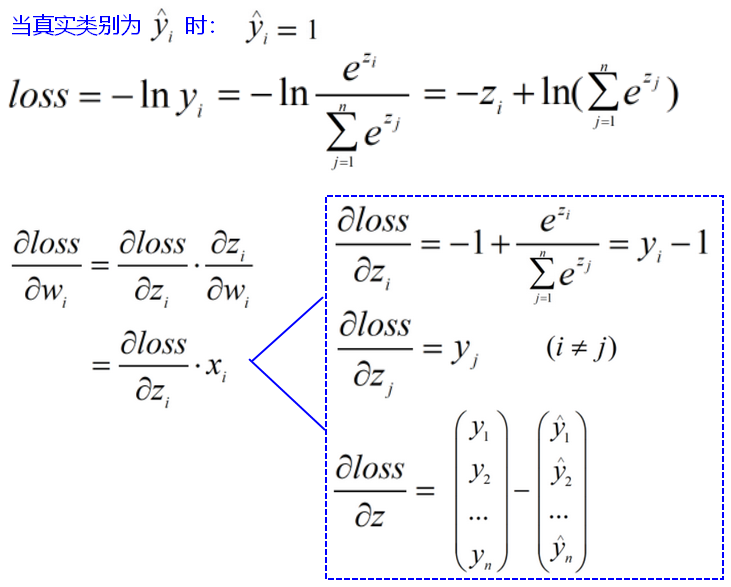
如果网络的输出层使用softmax进行多分类（手写数字的10分类），则损失函数为交叉熵：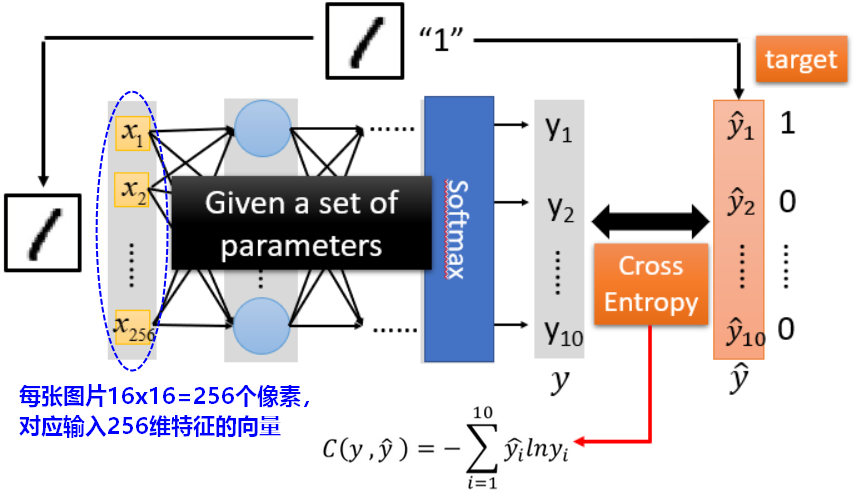
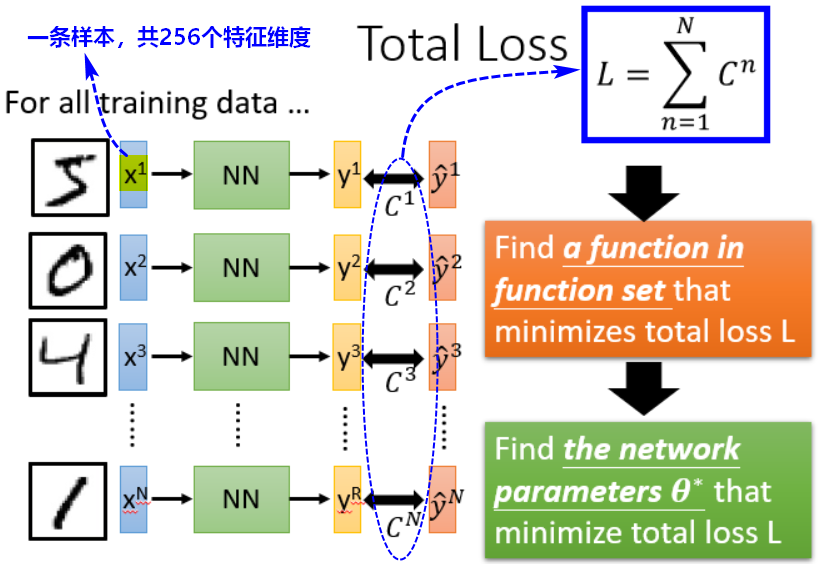
image.png
image.png

2.3选择最优模型

使用梯度下降求导、反向传播（backpropagation）来调整参数：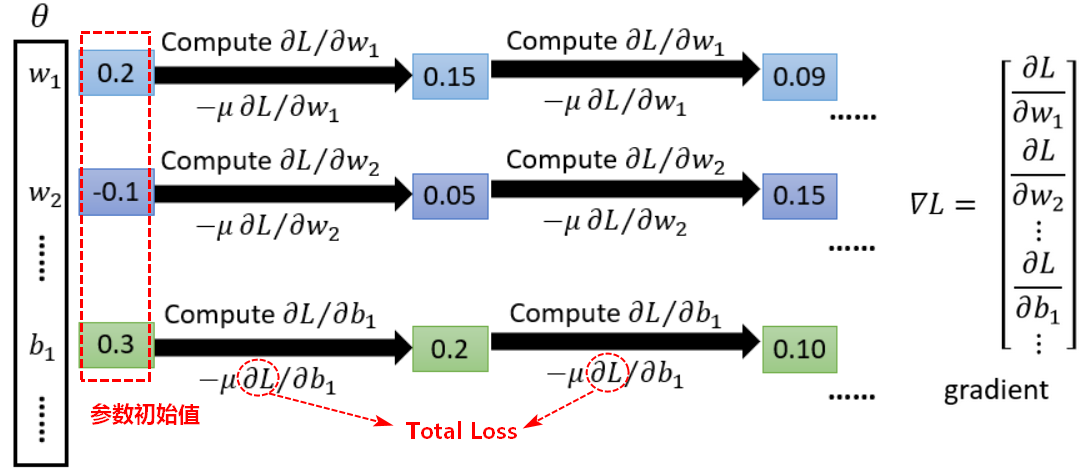
image.png

链式法则

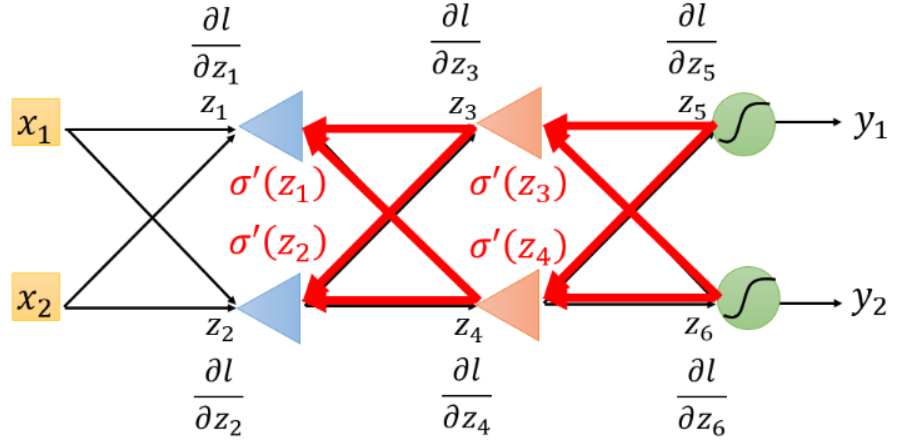
image.png

反向传播

神经网络中，反向传播可以更有效率计算梯度的向量（参数包括weight、bias）。
具有多个输出的神经网络可能有多个损失函数，而梯度下降过程必须基于单个标量损失值，因此需要将所有损失函数取平均，变成一个标量值。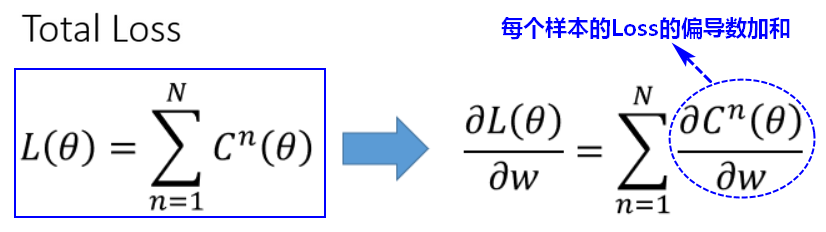
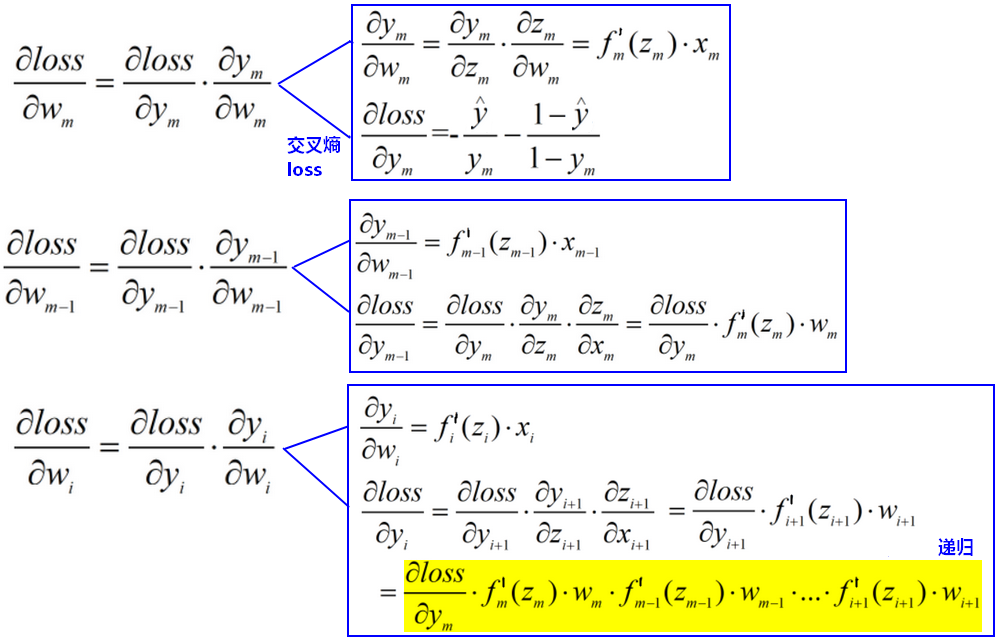
image.png
先单独拿出一个loss出来分析求导 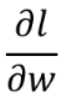image.png，其他loss也类似，最后加和就可以了。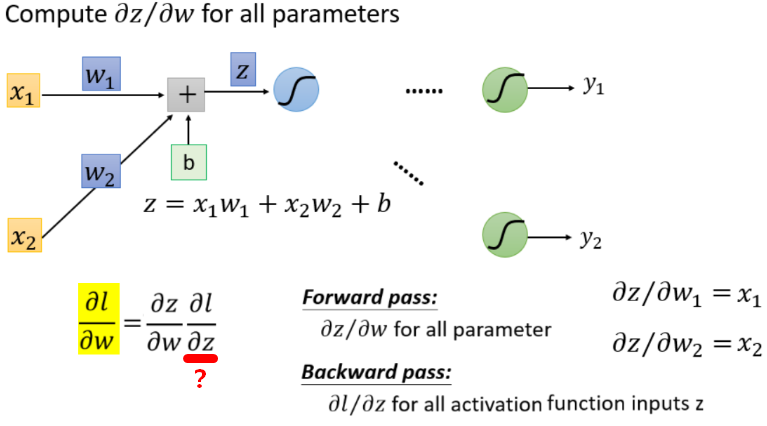
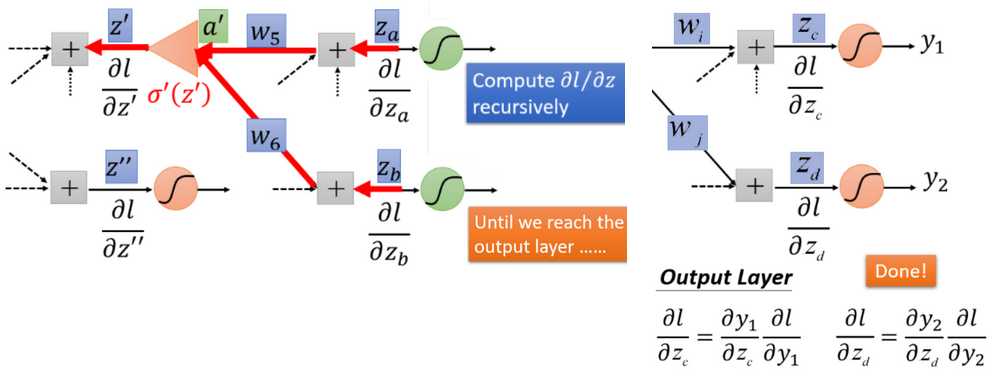
image.png
计算梯度分为前向和后向，前向容易求出，后向是层层嵌套的。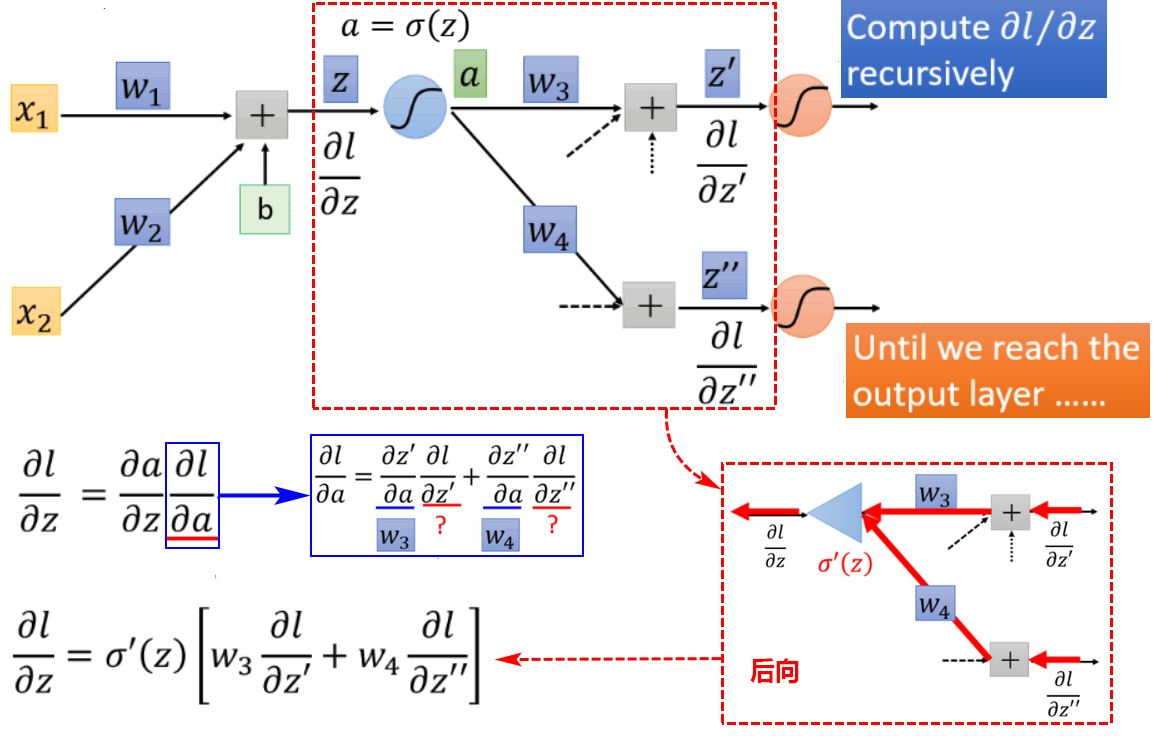
image.png
如果之后还有神经元，就利用后向的求导方式，反复往后计算，直到到达输出层。

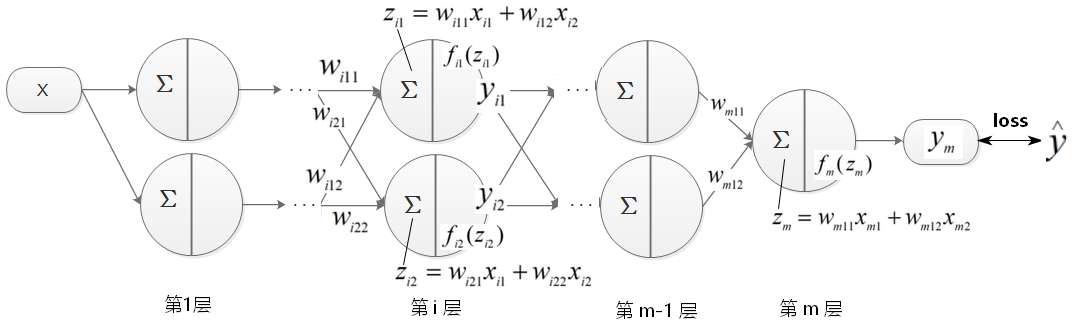
image.png
image.png

计算梯度：多层单神经元+sigmoid

image.png
image.png

梯度消失/弥散:Gradient vanishing

根据以上推导：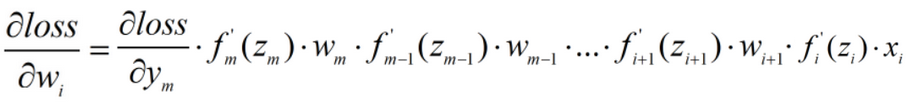
image.png
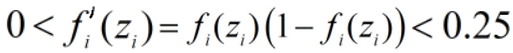
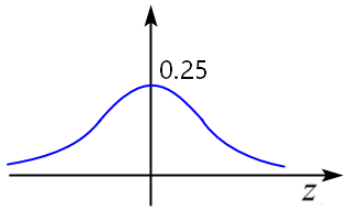当激活函数为sigmoid函数时，image.png
image.png，所以越是靠前的神经元（即接近原始输入的神经元），求出的梯度数值越小，梯度会渐渐趋近于0，此时参数w将不再有更新带来的变化，即不学习了。这种情况称为梯度消失或梯度弥散。
梯度消失相当于中间层对输入做了随机变换（因为w无法学习更新），然后再通过单个输出层输出。
梯度消失的根本原因是激活函数的导数太小，导致神经网络各层的梯度在数值上不是一个量级，对选择合适的学习因子带来困难。

梯度爆炸:Gradient exploding

根据以上推导，当激活函数的导数值较大时（例如：|df/dz|>1），层数增多的时候，最终的求出的梯度更新将以指数形式增加，会导致越靠近输入层的神经元，求出的梯度数值越大，最后溢出，这种情况称为梯度爆炸。

计算梯度：多层多神经元+sigmoid

image.png
image.png

计算梯度：多层多神经元+softmax

image.png
image.png

寻找最优参数：Mini-batch

以Keras为例，寻找最佳网络参数的代码为：
image.png
batch_size：表示一个batch中有多少条样本，数量一般设置为2^n。一个batch更新一次参数。
nb_epoch：程序跑完一遍所有的batch称为一个轮次epoch。例如：20轮次，表示每个batch被重复20次。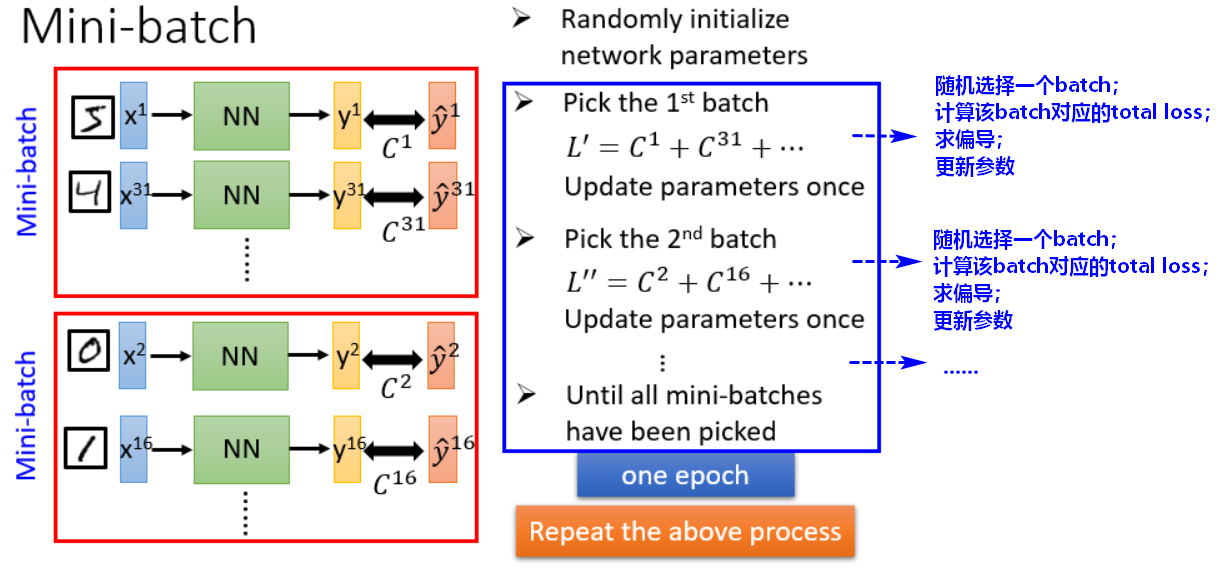
image.png

【问题】为什么要使用mini-batch来通过反向传播训练模型？
mini-batch代表使用了批量梯度下降，同样的训练集时，batch_size越小，一个轮次epoch中更新次数越多，耗时越长。batch_size设置较大（也不能太大），运算表现也较为稳定。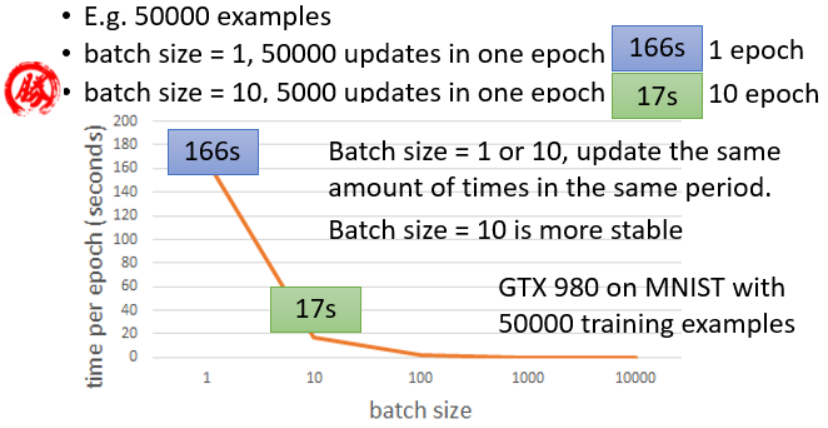
image.png
神经网络中的矩阵运算是并行的，利用GPU进行mini-batch运算，速度更快。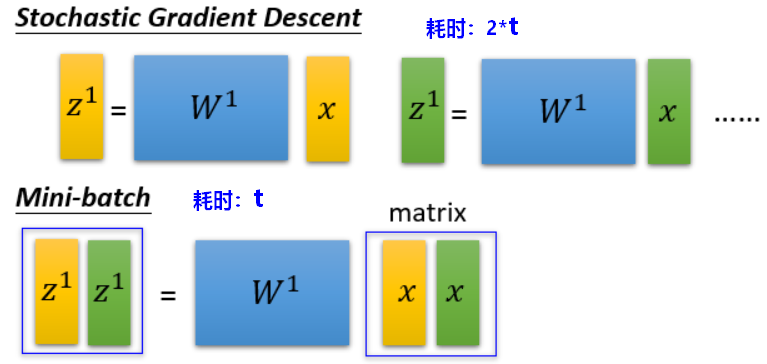
image.png

3.神经网络应用

3.1计算机视觉CV

  • 模式分类

  • 语义分割、实例分割

    Mask-RCNN

  • 目标检测

    Yolo

  • 目标追踪

  • 超分辨率

  • 视频分析

    3.2自然语言处理NLP

  • 文本分类

    1. 情感分析、用户兴趣分析、评论风向预测评估

  • 信息抽取

  • 自动文本摘要
  • 文本自动生成
  • 智能问答系统
  • 语音识别
  • 文本翻译
  • 图像翻译（CV+NLP）

  • 智能引擎推荐

    搜索、推荐、模式识别、知识图谱

    3.3控制科学与智能机器人技术

    控制理论、深度学习、强化学习、深度强化学习

来源： 1.台湾大学李宏毅Machine Learning (2017,Spring) 2.《Deep Learning with Python》Francois Chollet 3.北京邮电大学-人工智能导论