线性变换

1.什么是线性变换

“变换”本质上是函数的另一种说法，它接收输入内容并输出对应结果。线性代数的“变换”是接收一个向量并且输出一个向量。
如果某变换符合两个条件，它就是线性变换：
一是直线经变换后仍然保持为直线（一个向量就可以看成一条直线），不能有所弯曲；
二是原点必须保持固定。

2.向量的线性变换

因为向量可以表示为基向量的线性组合，对一个向量进行线性变换，可以认为就是对基向量做了线性变换。经线性变换后的向量，是“线性变换后的基向量”用同样的标量数乘并加和得到的线性组合：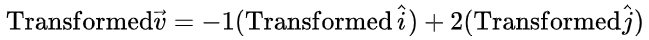

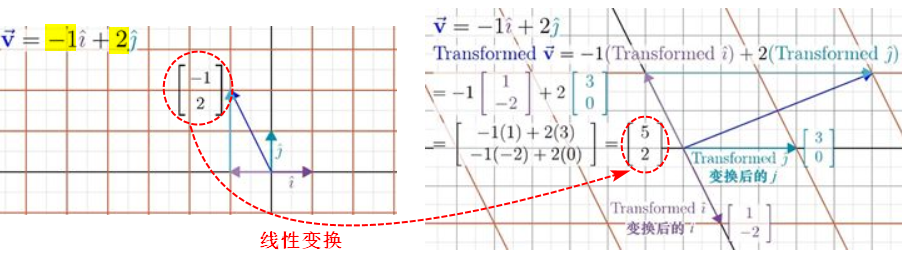
矩阵与向量乘法

对向量进行线性变换，等同于向量与矩阵相乘：只需要将该向量坐标作为数乘标量代入计算，该矩阵的每一列就是线性变换后的基向量。
所以一个二维线性变换仅用4个数字（即基向量对应的一共4个坐标值）就可以完全确定。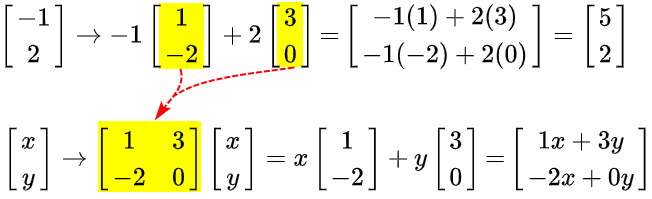

一般的：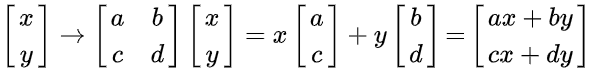

2x2矩阵的列向量若线性相关，则其所对应的线性变换就是将二维空间压缩成列向量所在的直线。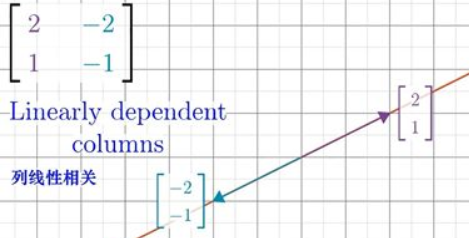

映射mapping

通过线性变换使得平面内的一个向量变为平面内的另一个向量，这种变换关系通常称之为“映射”（mapping），例如：（输入一个二维向量，输出一个二维向量）。

• 线性变换规则

对于任意向量，标量，线性变换的规则：

• 矩阵与向量相乘

因为对向量进行线性变换，就是矩阵与向量相乘，所以可以把函数看成矩阵乘法：
对于矩阵，向量，标量，有：

【例如】对于线性变换：，相当于矩阵相乘：，其中是二维向量，是3x2矩阵，结果是一个三维向量。

描述线性变换

二维平面内，如果已知两个线性无关的向量和它们线性变换的结果，根据线性变换规则，可以通过其线性组合，了解平面内所有的向量线性变换的结果：

如果想了解线性变换对整个输入空间的影响，只需确定它的一组基线性变换的结果。
如果用矩阵来表示线性变换，则需要两组基，即输入空间的一组基和输出空间的一组基，来分别确认输入向量与输出向量的坐标；用矩阵来表示线性变换就是将向量的坐标乘以矩阵得到它在输出空间的坐标。

矩阵代表输出空间的一组基，输出空间的坐标是输出空间的基进行线性组合所需的系数。

来源： 1.MIT-线性代数笔记：https://zhuanlan.zhihu.com/p/46119592