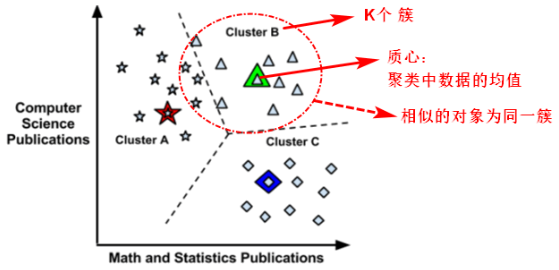
1.KMeans：思想和步骤
- 【初始化中心点】在样本特征范围内，随机选择K个中心点/质心；
- 【分簇、聚类】计算每个样本点到K个中心点的距离（例如：欧式距离），对于一个样本点来说，在这K个距离中，哪个距离最近，该样本点就属于哪个中心点所在的组/簇（cluster）；
- 【更新中心点】在每个组/簇内求均值(每个方向上的均值)，重新确定中心点的位置；
- 【迭代】重复第二步、第三步操作，多次迭代，进行分簇聚类和确定中心点；
- 【停止】直到中心点的位置相对稳定，说明已经聚好类，可以停止迭代。
2.KMeans：核心问题
2.1聚类的评价：轮廓系数
- 簇内不相似度：样本点i到同簇内其他点的平均距离
被称为点i的簇内不相似度，越小，说明越应该被聚到该簇。 - 簇不相似度：一个簇内所有点的簇内不相似度的均值，是该簇的簇不相似度。簇不相似度小，则是高内聚。
- 簇间不相似度：样本 i 到其他簇
中所有样本的平均距离
称作是样本 i 与簇 
的不相似度。定义样本 i 的簇间不相似度为： 
= min(bi1, bi2…bik)。 越大说明样本 i 越不属于其他簇。
轮廓系数（silhouette coefficient）:
当
时，
;
当
时，
;
当
时，
;
对于好的聚类，我们希望簇内不相似度越小越好，簇间不相似度
越大越好。所以
越接近1，则聚类越合理；越接近-1，则样本更适合被聚到其他类；越接近0，则样本在两个类的边界上。
2.2中心点：数量K的选择
- 方法一：根据业务场景选择K，例如：用户分为高收入、中收入、低收入等。
- 方法二：手肘法（Elbow method）。
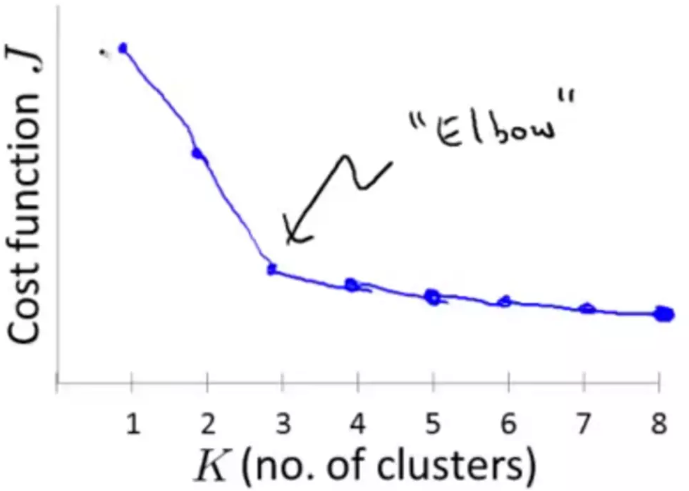kmeans中的损失函数为各个簇类中，各自所有的样本点到所在簇中心点的距离之和。假设一共有K个簇，
表示第m个簇内的第i个样本点，
表示第m个簇的中心点，则：
，loss越小越好。
随着k值的增大，loss逐渐减小，但k增大到某个值之后，聚类的收益
越来越小，在某个点(k=n)处，收益发生较大变化，且此后收益变化较小，这个拐点就是应该选择的K值。
2.3中心点：位置的选择
2.4 kmeans的缺点
- 受异常点影响大
kmeans在根据均值确定中心点位置时，受异常点/离群点的影响较大，因此需要先去掉异常点。
求出每个点与其他点的距离之和，距离最大的那个就是异常点。
- 数值问题：某些特征的数值差异
例如：用户的数据样本=(身高，体重)，当特征的单位不同时，特征值的数值大小差异较大，这样聚类效果容易被数值差异较大的特征所主导，因此需要在特征间做量级的归一化。
- 数值问题：某些场景缺乏解释性
kmeans算法中需要取数值均值来确定中心点位置，但某些特征使用数值时，不具有可解释性。例如：用户的性别特征，作为均值的小数，对性别不具备实际的可解释性。
- 无法解决中心点一致的数据的聚类
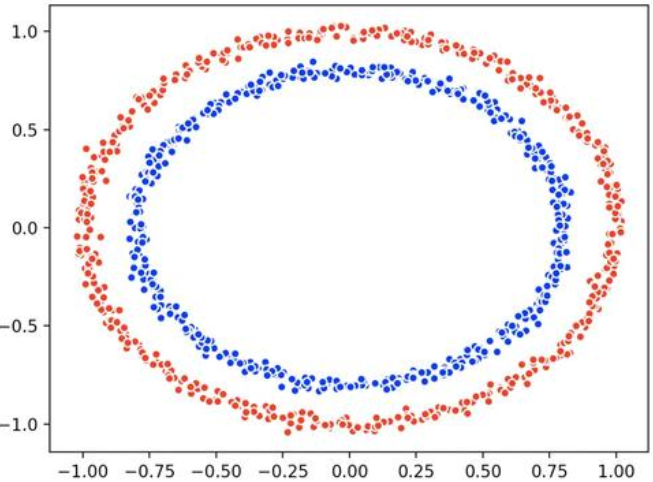数据分布差异大，但中心点一致的数据，无法使用kmeans进行较好的聚类，此时可以使用DBScan。
3.KMeans：应用
3.1 KMeans+分类器
- 训练过程：先用KMeans聚类（无监督学习，不用标签），再针对聚出的每个类簇，分别训练分类器（有监督学习，使用标签），例如：使用逻辑回归算法训练分类器。
测试过程：对于一个新的样本点，先找到其所属的类簇，再用相应的分类器进行分类。
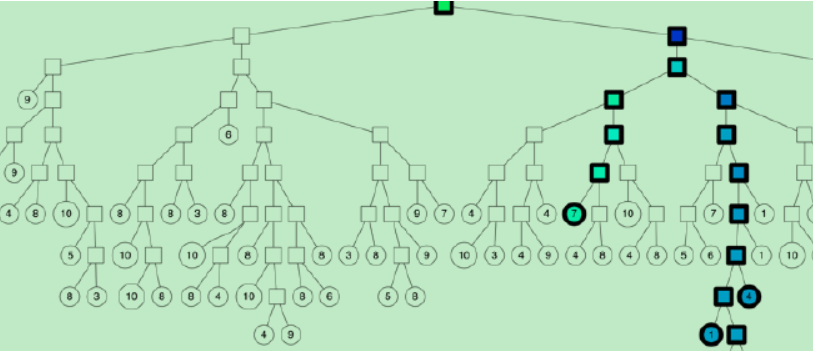
3.2 KMeans+KNN：annoy
Annoy（Approximate Nearest Neighbors Oh Yeah）是高维空间求近似最近邻的一个开源库，即给定给一个查询点，在空间搜索和它相近的点。
【问题】在高维空间，直接进行最近邻的距离计算，计算量大。
【假设】Annoy的目标是建立一个数据结构（二叉树），使搜索最近邻点的时间复杂度是次线性O(log n)。Annoy建立这样的二叉树结构是希望满足这样的一个假设: 相似的数据节点应该在二叉树上位置更接近，一个分割超平面不应该把相似的数据节点分割二叉树的不同分支上。
【解决】使用KMeans将数据集分为两个类簇，再继续对这两个类簇进行聚类，以此类推，二叉划分，形成一棵树（叶子节点记录原始数据，中间节点记录分割超平面的信息）。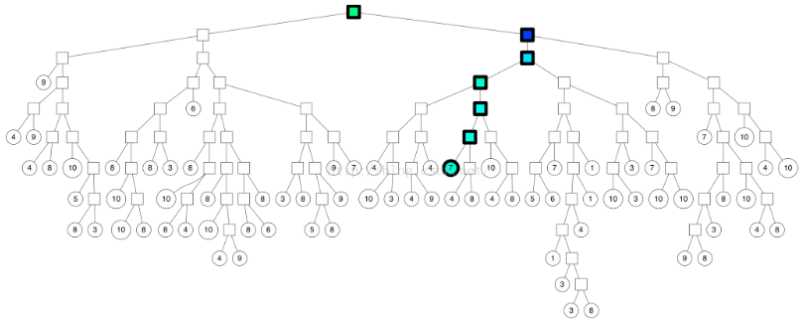
【annoy具体流程】随机选择两个中心点，进行KMeans聚类。
- 将聚类后收敛的新的中心点连接，过连接线中心作垂直线/面，得到分割线/超平面。
- 在分割后的子空间重复进行上述操作，直到每个子空间最多剩下K个数据点。
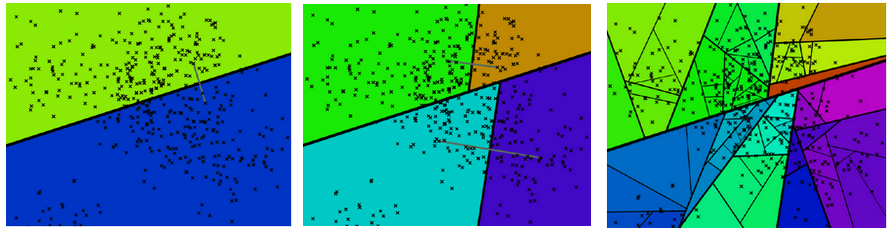
【问题】二叉树中，原本相邻的数据被分到不同的分支，造成寻找最近邻的结果不准确，怎么办？
方法一：进行多次建树（annoy.build），保存索引。对于一个新的样本点，应用到多棵树中，对求出最近邻的结果取并集去重。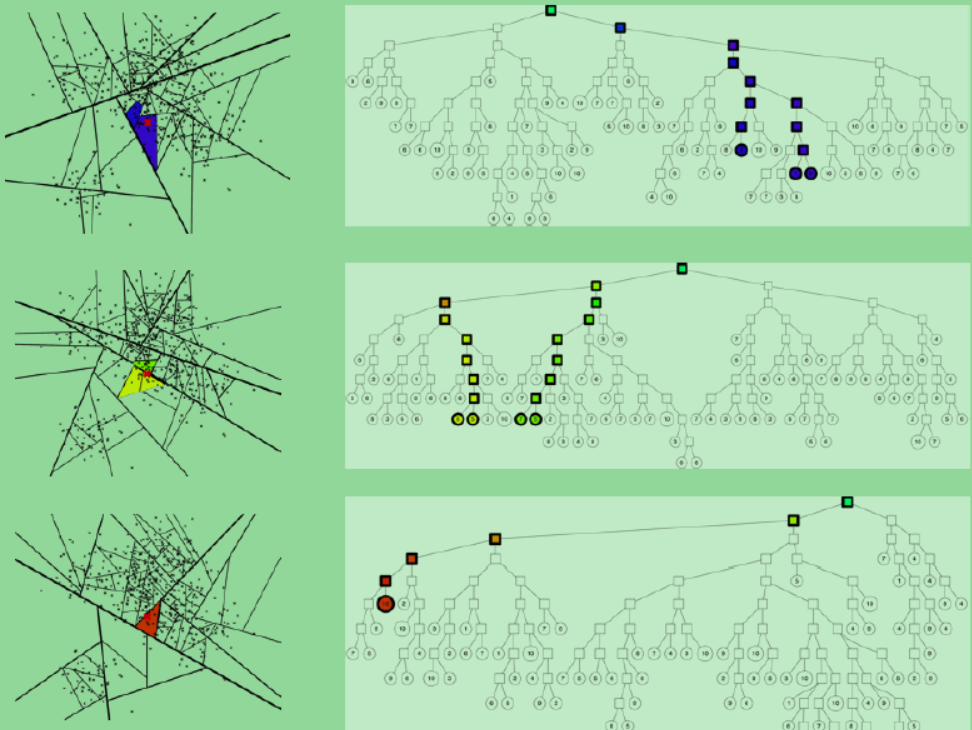
方法二：一次建树，如果分割超平面的两边都很相似，那可以两边都遍历。
若有收获，就点个赞吧
0 人点赞
