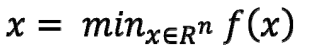1.函数最优化问题
1.1 无约束条件的最优化问题
1.2 有约束条件的最优化问题
以下约束条件中没有考虑 >0 的情况,因为可以由小于等于0反推出来。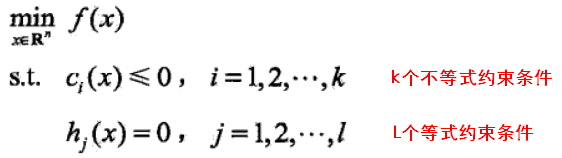
将以上最优化问题命名为原始(最优化)问题。
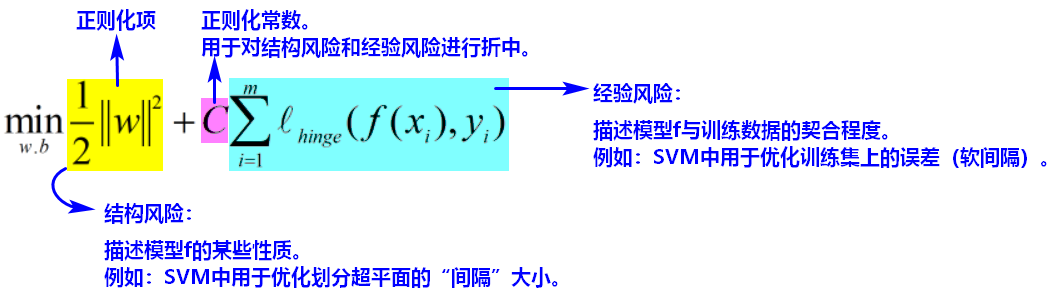
凸优化问题:对于上述有约束条件的最优化问题,目标函数 f(x) 和约束函数 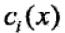 都是R上连续可微的凸函数,
都是R上连续可微的凸函数,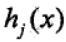 是R上的仿射函数(满足
是R上的仿射函数(满足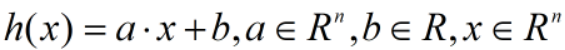 )
)
1.3 求解最优化问题
1.4 拉格朗日函数
拉格朗日函数是将原始问题的f(x)和约束条件进行整合,
使有约束条件的最优化问题>>>>>转为>>>>>无约束条件的最优化问题。
使原始问题的一次优化问题>>>>>转为>>>>>极小极大的二次优化问题。
二次规划(quadratic programming
)
在约束最优化问题中,常利用拉格朗日对偶性(Lagrange duality)将原始问题转换为对偶问题,通过求解对偶问题得到原始问题的解。
拉格朗日乘子(Lagrange multiplier):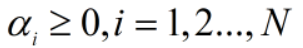
拉格朗日乘子向量: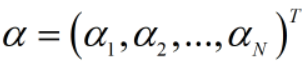
拉格朗日函数的特性
极小极大
由拉格朗日函数的特性可知,当x满足原始问题约束时,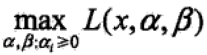 就是原始问题的f(x),此时进行极小化就等同于对原始(最优化)问题进行极小化,解是相同的,即:
就是原始问题的f(x),此时进行极小化就等同于对原始(最优化)问题进行极小化,解是相同的,即: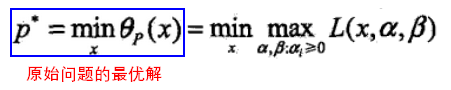
对偶问题
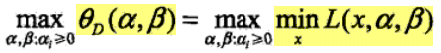 被称为拉格朗日函数的极大极小问题,也被称为原始问题的对偶问题。
被称为拉格朗日函数的极大极小问题,也被称为原始问题的对偶问题。
定义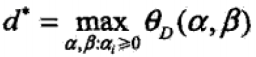 为对偶最优化问题的最优解,当 f(x)和
为对偶最优化问题的最优解,当 f(x)和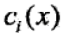 为凸函数,
为凸函数,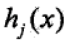 是仿射函数时,有:
是仿射函数时,有: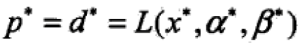 ,其中的约束条件为KKT(Karush-Kuhn-Tucker)条件:
,其中的约束条件为KKT(Karush-Kuhn-Tucker)条件:
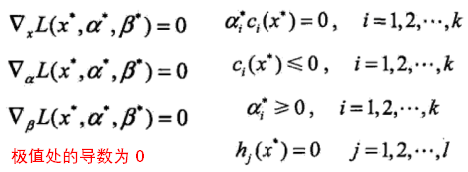
2.Support Vector Machine
SVM:线性的分类(二分类)算法。
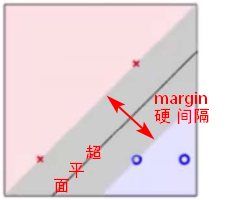
基本思想:求解能够正确划分训练数据集,且几何间隔最大的分离超平面。间隔最大化,意味着以充分大的确信度对训练数据进行分类。
支持向量机(Support Vector Machine)是Cortes和Vapnik于1995年首先提出的,它在解决小样本、非线性及高维模式识别中表现出许多特有的优势。
2.1 线性可分SVM
线性可分性
给定一个数据集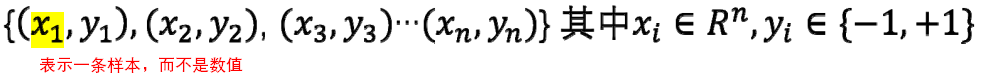 ,如果存在某个超平面
,如果存在某个超平面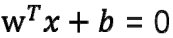 ,满足:
,满足:
- 将数据集的正实例点和负实例点完全正确的划分到超平面的两侧;
- 对所有
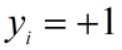 的实例,都有
的实例,都有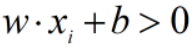 ;对所有
;对所有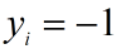 的实例,都有
的实例,都有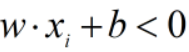 。
。
则称以上数据集是线性可分(linearly separable)的。
模型判别式:
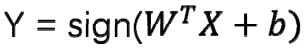 ,是线性的公式,本质是在高维空间找到一个超平面来分隔数据。
,是线性的公式,本质是在高维空间找到一个超平面来分隔数据。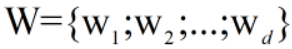 是法向量,决定超平面的方向,b 是位移项,决定超平面与原点距离。
是法向量,决定超平面的方向,b 是位移项,决定超平面与原点距离。
【问题】通常这样用于分隔的超平面有很多,哪一个最好?
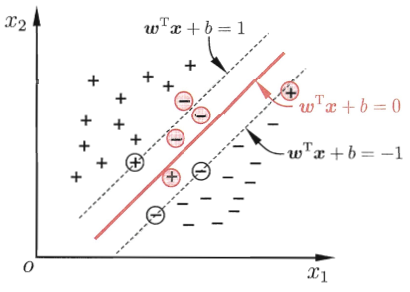
最好的超平面:
- 完美的分类正负例
- 距离最近的点越远越好(对点位置变动的容忍度大),即硬间隔越大越好。(最大间隔法)
- (根据以上两点确定的超平面,求出y=0时的w值和b值。)
几何距离和函数距离
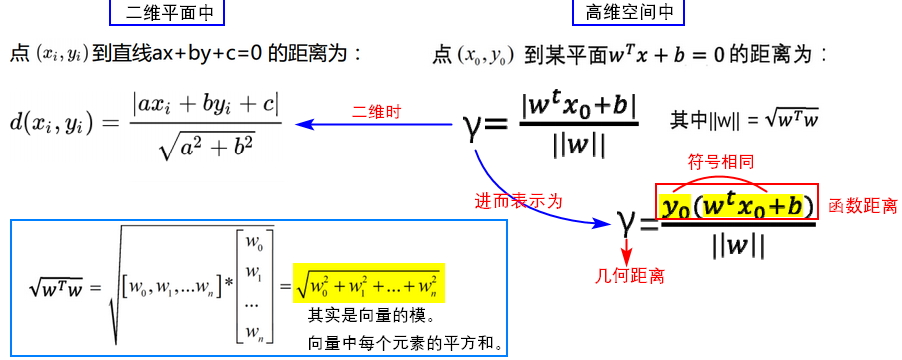
函数距离(functional margin)可以表示分类的正确性和分类预测的确信度。
损失函数与优化
- 根据距离公式,可以将最好的超平面的定义转换为函数的最优化问题:

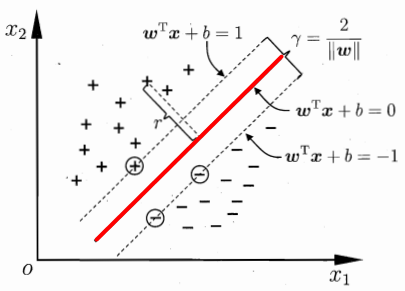
如果将 w 和 b 等比例缩放为 λw 和 λb,函数间隔变成 λγ’,函数间隔的改变对不等式约束没有影响,对目标函数的优化也没有影响。于是,为了方便求解,直接令 γ’ = 1,改变上述最优化问题,得到
决策超平面的标准表示:

即 在线性可分的SVM中,假设超平面可以将样本正确分类,则有当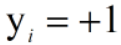 时,
时,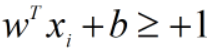 ;当
;当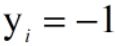 时,
时,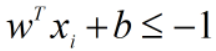 。
。进一步根据上述最优化问题,构建拉格朗日函数:

- 根据对偶函数,先求极小值
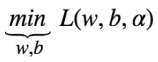 ,拉格朗日函数分别对 w 和 b 求导,求出 w 和 b 各自与 α 的关系。
,拉格朗日函数分别对 w 和 b 求导,求出 w 和 b 各自与 α 的关系。
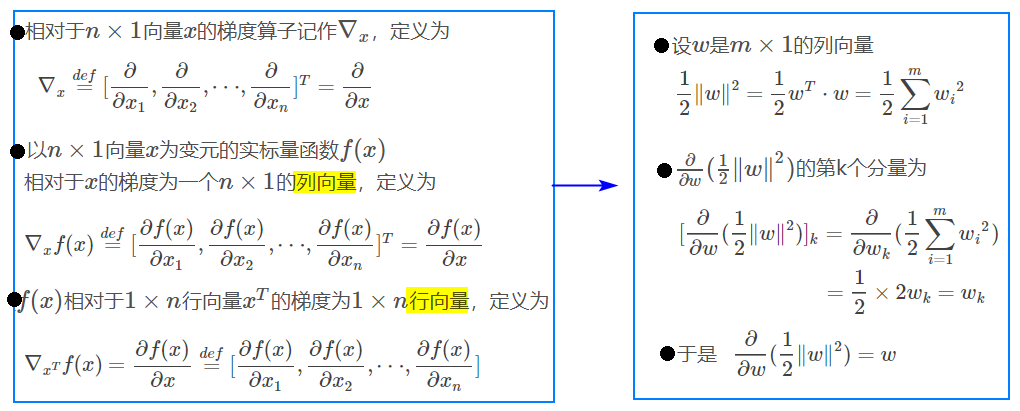
根据以上推导,求导得出: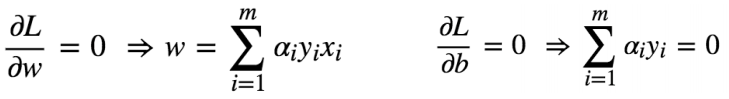
- 将求导结果代入原来的函数:
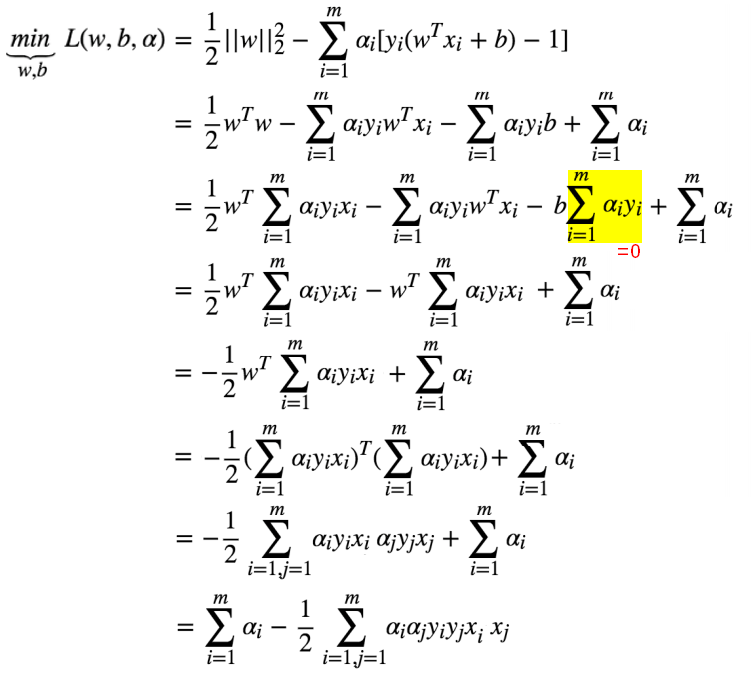
- 进一步转换对偶问题的优化问题为:
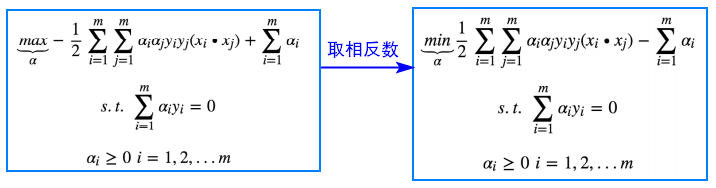
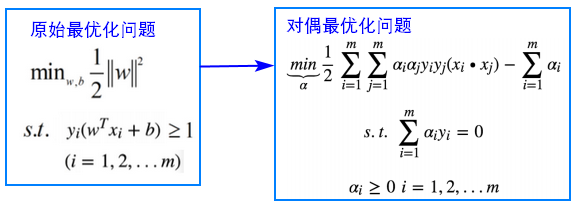
- 通常使用SMO算法(序列最小最优化算法)进行求解,可以求得一组 α使得函数最优化。求解之后,α成为已知数,根据KKT条件,再求出 w,b .
模型与支持向量
将求出的w与b代入模型判别式: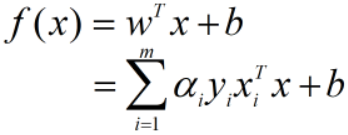
根据KKT条件,
若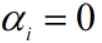 ,则该样本不会出现在模型判别式中,对f(x)没有影响;
,则该样本不会出现在模型判别式中,对f(x)没有影响;
若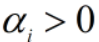 ,则
,则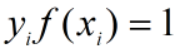 ,对应的样本点出现在最大间隔边界上,是支持向量。
,对应的样本点出现在最大间隔边界上,是支持向量。
【结论】模型判别式只与支持向量有关,大部分样本都不需要保留,保持了稀疏性;或者认为模型与所有样本相关,只不过当样本不是支持向量时,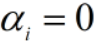 。
。
2.2线性SVM
线性不可分、软间隔、损失函数
为了得到最好的分隔超平面,满足的条件有:
- (满足约束条件时)可以把正负例完美分开
- 找到间隔最大的点(函数优化问题)
对于线性不可分问题,会有噪声点,不满足线性可分SVM中的约束条件,为了放松约束条件,而引入松弛变量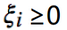 。ξ代表异常点嵌入间隔面的深度,我们要在能选出符合约束条件的最好的w和b的同时,让嵌入间隔面的总深度越小越好。
。ξ代表异常点嵌入间隔面的深度,我们要在能选出符合约束条件的最好的w和b的同时,让嵌入间隔面的总深度越小越好。
当所有样本都正确分类时,间隔带称为硬间隔(hard margin),此时样本都满足约束: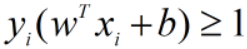
当某些样本不满足约束条件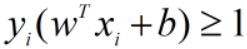 是,间隔被称为软间隔(soft margin),我们希望不满足约束条件的样本越少越好。
是,间隔被称为软间隔(soft margin),我们希望不满足约束条件的样本越少越好。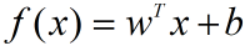 ,当y=+1或y=-1时,正确分类情况下
,当y=+1或y=-1时,正确分类情况下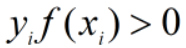 ,特别的,对于硬间隔的情况,
,特别的,对于硬间隔的情况, ,并且乘积越大越好;错误分类的情况下,
,并且乘积越大越好;错误分类的情况下,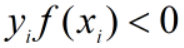 。
。
SVM损失函数需要考虑到两种情况:错误分类的情况;软间隔的情况。
理想的损失函数(0/1损失函数)是希望不满足约束条件的样本越少越好: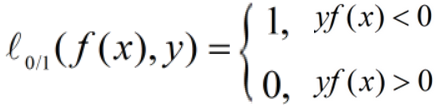
(0/1损失函数其实只考虑了错误分类的情况。)
总体损失函数可写为: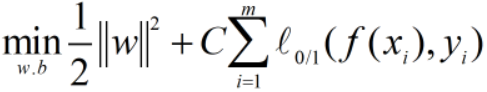
替代损失、hinge损失
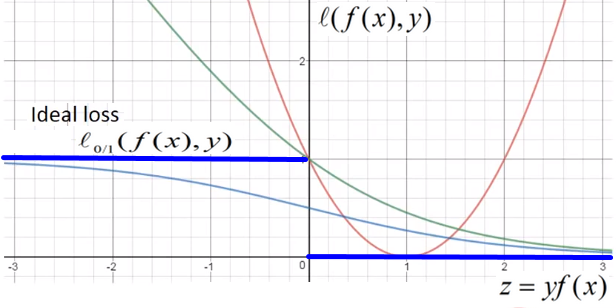
以上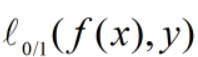 是非凸、非连续的,不是连续可导的,不易求解,因此寻找其他函数来代替,称为替代损失(surrogate loss)。
是非凸、非连续的,不是连续可导的,不易求解,因此寻找其他函数来代替,称为替代损失(surrogate loss)。
另外0/1损失函数没有保证分类的足够高的确信度,于是使用0/1损失的上界—-hinge损失来构造损失函数。
其中,hinge损失(合页损失函数):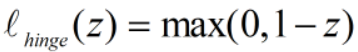 ,
,
我们希望硬间隔完全正确分类的情况下,损失loss=0,此时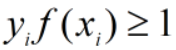 ;其他情况(包括错误分类和软间隔),随着
;其他情况(包括错误分类和软间隔),随着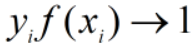 ,损失越来越小,loss—>0。
,损失越来越小,loss—>0。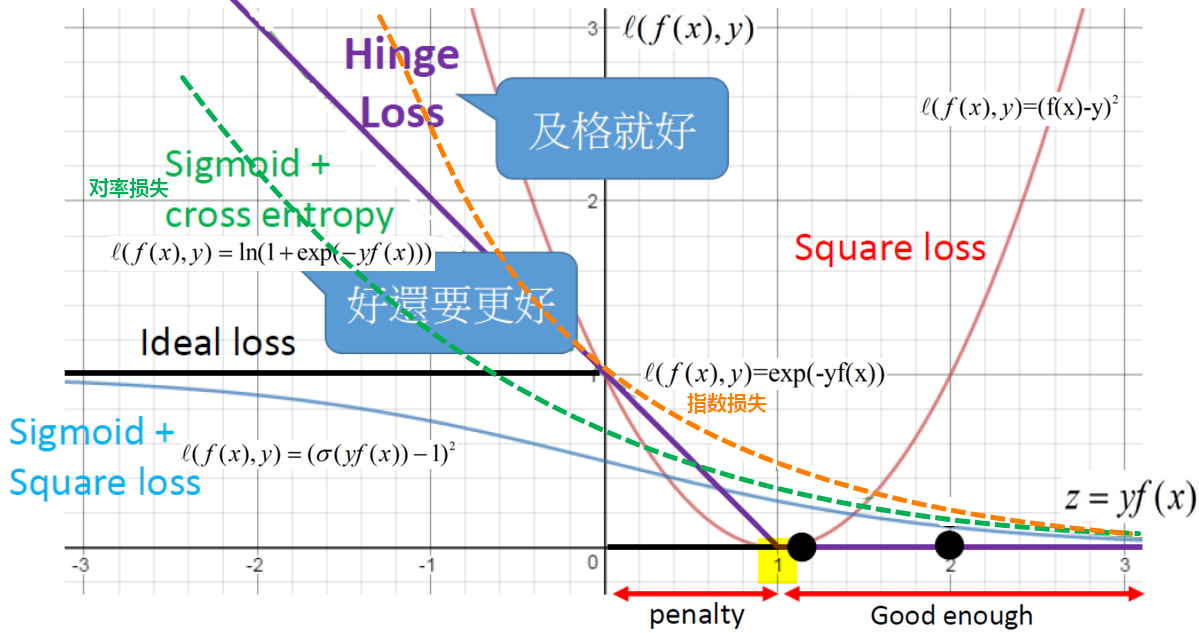
当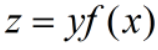 时,总体损失函数为:
时,总体损失函数为: ,
,
令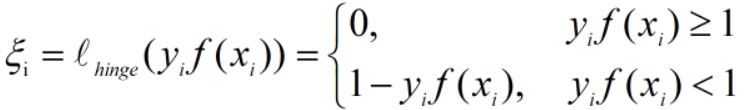 ,有
,有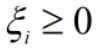 ,条件分析如下:
,条件分析如下:
当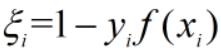 时,是软间隔情况下的取值,软间隔/硬间隔的情况同时考虑时,有:
时,是软间隔情况下的取值,软间隔/硬间隔的情况同时考虑时,有: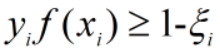 ,
,
总体的损失函数为:
优化目标分析
最优化问题
- 线性SVM的原始问题(凸二次规划问题)如下:

- 分类决策函数
求出原始问题的最优解,代入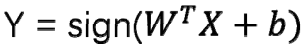 ,即得到分类决策函数。
,即得到分类决策函数。
分离超平面为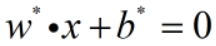
- 构建拉格朗日函数
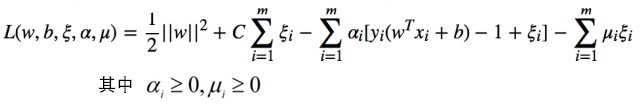
- 求解
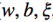


- 用SMO算法求出 α*.
网格搜索
【问题】如何确定正则化常数 C 的取值?
C是一个超参数(即无法通过直接的数学计算求解的参数),可以在一个范围内为C赋n个值,分别得到n个模型,通过有效集来验证n个模型的误差,选择最好的模型所对应的C的值。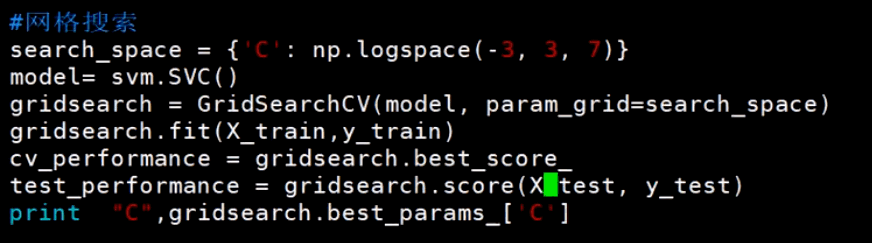
模型与支持向量

SVM模型判别式的另一种表示: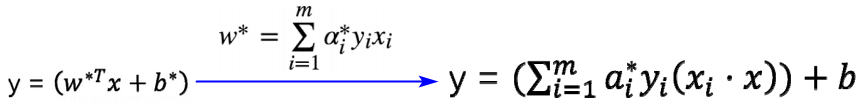
【结论】:软间隔SVM的最终模型和支持向量以及分类错误点有关,使用hinge损失函数时保持了稀疏性。
**
2.3非线性SVM
SVM升维
为了处理线性不可分问题,可以引入升维,即把原始的 x 映射到更高维度的空间: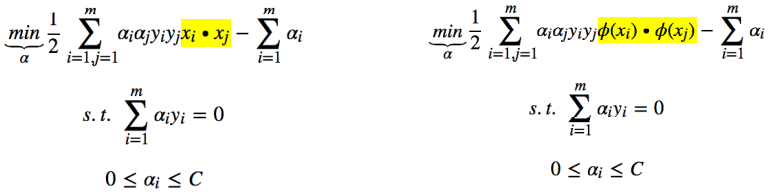
【问题】升维之后,再做向量的内积,会出现维度爆炸。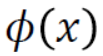 相当于是在做特征转换(feature transformation),
相当于是在做特征转换(feature transformation),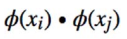 即是先做特征转换再做内积,这种运算耗时而且可能会有无穷维。
即是先做特征转换再做内积,这种运算耗时而且可能会有无穷维。
【解决】引入核函数。思路:不具体计算向量的内积,而是直接定义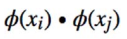 的结果。
的结果。
通过核方法,引入核函数,将线性学习器拓展为非线性学习器,将原始样本空间映射到另一个合适的特征空间。
核技巧 kernel trick
例如:
将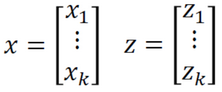 升维后,(假设我们知道升维后的形式)得到
升维后,(假设我们知道升维后的形式)得到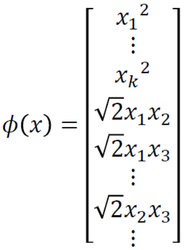 ,此时如果直接计算
,此时如果直接计算 ,计算量大。
,计算量大。
而引入核函数之后,直接转化为K(x,z)的计算,核函数和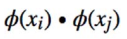 的计算是等价的。
的计算是等价的。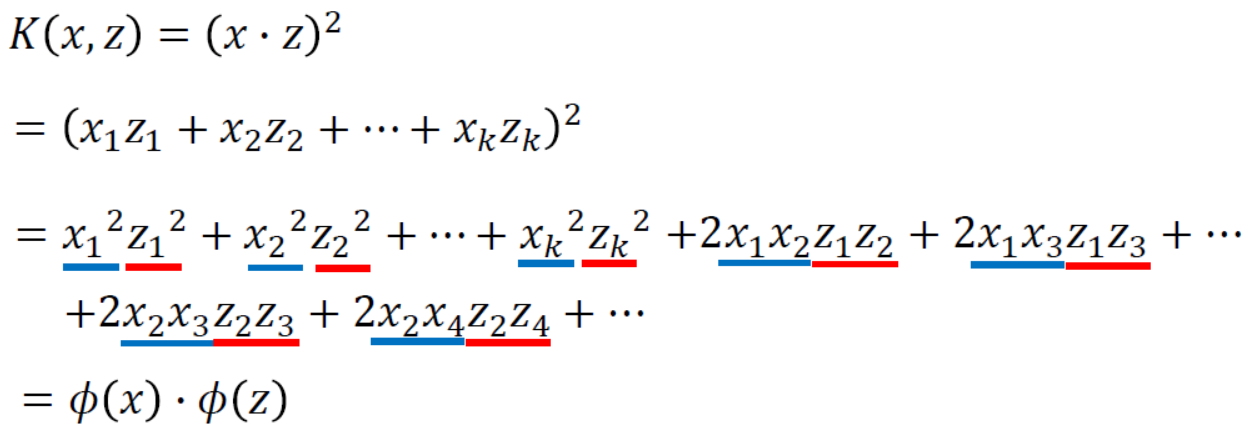

核函数

核函数判断:
如果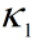 和
和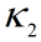 是核函数,
是核函数,
- 对于任意正数
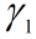 、
、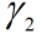 ,线性组合
,线性组合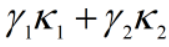 也是核函数。
也是核函数。 - 核函数的直积
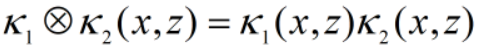 也是核函数。
也是核函数。 - 对任意函数
 ,
,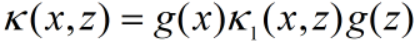 也是核函数。
也是核函数。
2.4 SVM算法总结
算法流程
- 选择核函数及对应的超参数;
- 选择惩罚系数C;
- 构造最优化问题;
- 利用SMO算法求出一组 α* ;
- 根据 α计算w
- 根据α*找到全部的支持向量,计算每个支持向量对应的
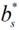
- 对
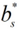 求均值,得到 b*
求均值,得到 b* - 得到判别函数和超平面。
算法优劣
【优点】:SVM使用边界点作为支持向量来找出分类界限,边界点以外的样本点如何分布对分类模型没有影响,抗数据扰动,抗噪声。
【缺点】:SVM的分类结果只有几何意义,丧失了概率意义。
必须遍历所有数据点,才知道哪个是边界点,所以数据点之间是耦合的。当数据量非常大时,对硬件要求高,因为需要所有数据点,做分布式也受限。
【参考】 1.《统计学习方法》第二版 李航著; 2.https://blog.csdn.net/u014540876/article/details/80172623 3.《PRML》 4.《机器学习》周志华 5.台湾大学李宏毅《机器学习》课程