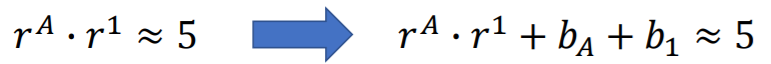1.MF介绍

1.1 概念

矩阵因式分解Matrix Factorization，即找到两个（或更多）的矩阵，将它们相乘便可以得到原来的矩阵，这相当于将原来的矩阵进行了分解。

1.2 示例

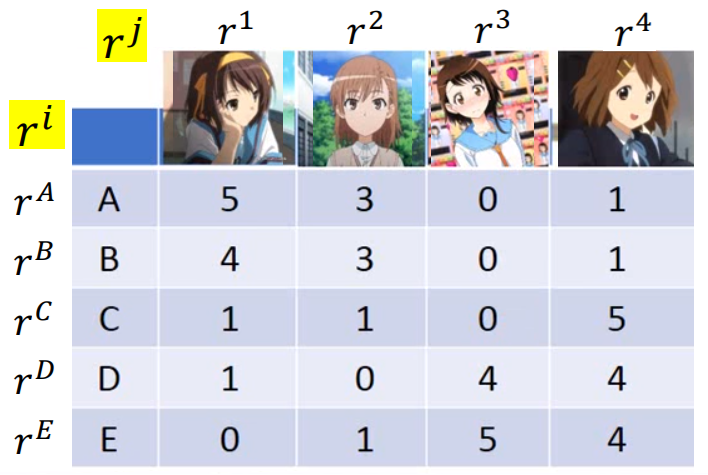
image.pngimage.png
这是用户对购买公仔的评分表，在相似的购买行为背后，或同样受欢迎的公仔背后，隐藏着一些决定决定购买行为或商品是否受欢迎的隐藏属性因素（latent factor），例如：用户的性格、喜好等，商品的特点等；并且用户的隐藏因素量=商品的隐藏因素量。

SVD

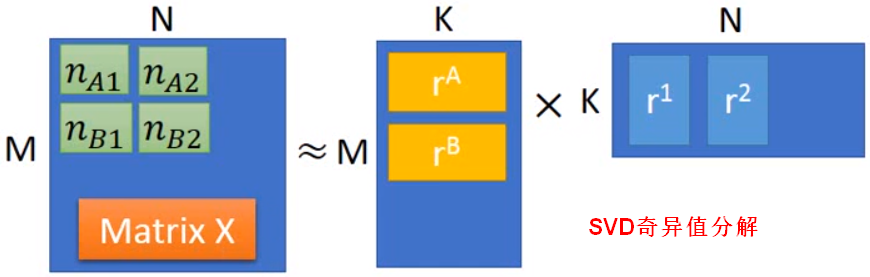
假设用户的数量为 M，公仔的数量为 N，隐藏属性因素的数量为 K。
将这些隐藏因素表示为向量，Matrix Factorization - 图3表示用户的隐藏属性，Matrix Factorization - 图4表示商品的隐藏属性，二者存在如下关系：
Matrix Factorization - 图5，即 Matrix Factorization - 图6，将评分的矩阵进行奇异值分解可得（两边的值越接近越好）：
image.png

损失函数1

如果评分矩阵中存在缺失值，此时不能直接使用SVD，可利用损失函数对缺失值进行填充/预测。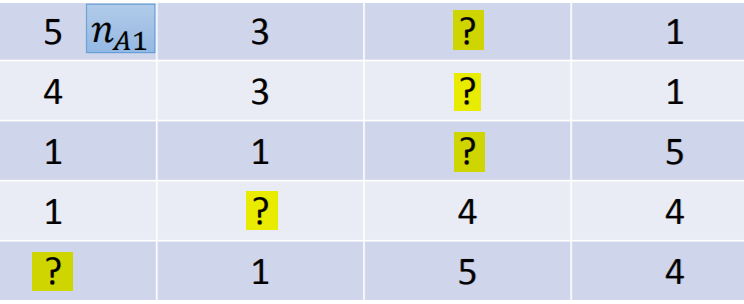
image.png image.png
Matrix Factorization - 图10，只考虑已知评分数值的项。
使用梯度下降可以求解出Matrix Factorization - 图11，根据 Matrix Factorization - 图12可计算出缺失值。

损失函数2

除了考虑用户和商品的隐藏属性因素，还可以加入用户的特性Matrix Factorization - 图13（比如：资金雄厚，购买力强）、商品的特性Matrix Factorization - 图14（比如：更受男性欢迎）。

image.png
损失函数变为：Matrix Factorization - 图16，同样用梯度下降求解，可以加入正则项。

2.MF应用

2.1推荐系统

矩阵因式分解可以用来发现在两类有相互关系的实体之中的隐藏（latent）属性信息。在协同过滤中预测打分，以便将相应的物品/条目推荐给用户。

2.2主题分析

LSA（Latent Semantic Analysis）

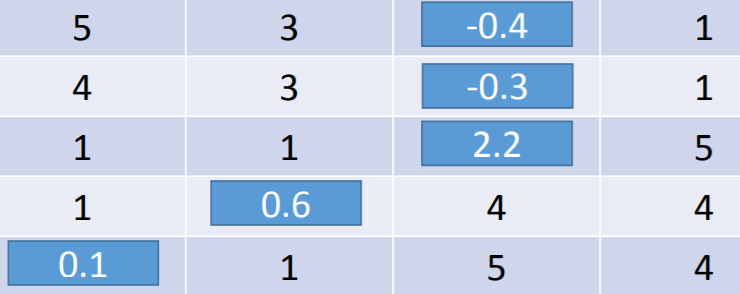
表格中的数值可以是TF-IDF；隐藏的属性因素为主题（topic）。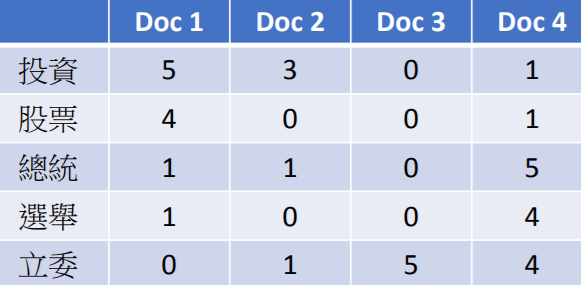
image.png
PLSA（Probability Latent Semantic Analysis）
LDA（Latent Dirichlet Allocation）

参考来源： 1.李宏毅《机器学习》2017 2.矩阵因式分解的Python实现：http://www.quuxlabs.com/blog/2010/09/matrix-factorization-a-simple-tutorial-and-implementation-in-python/