偏差-方差

1. 期望值

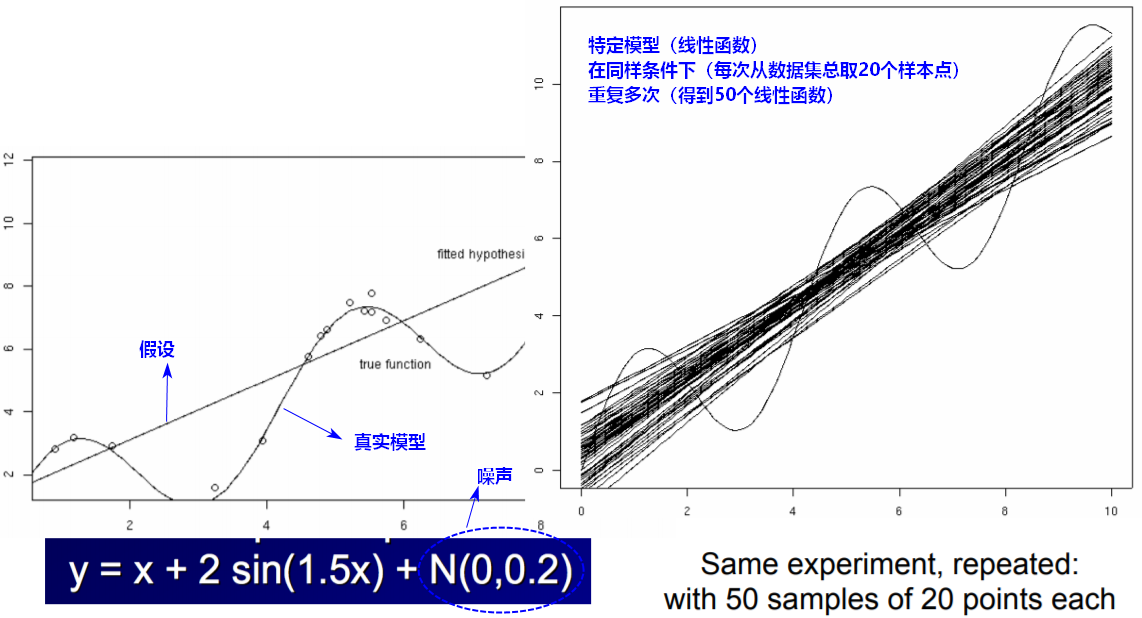
期望值是在同样的条件下重复多次随机试验，得到的所有可能状态的平均结果。
对于机器学习来说，
【同样的条件】就是选择一种算法（并选定超参数），训练集大小固定，得到一个特定的模型。
【重复多次的随机试验】每次训练时从样本空间中选择一批不同的样本（但数量相同）作为训练集，重复进行多次训练，每次训练会得到一个具体的模型。每个具体模型对同一个未见过的样本进行预测可以得到预测值。
【期望输出】多个预测值的平均值就是预测值的期望值。

2. 偏差-方差：示例

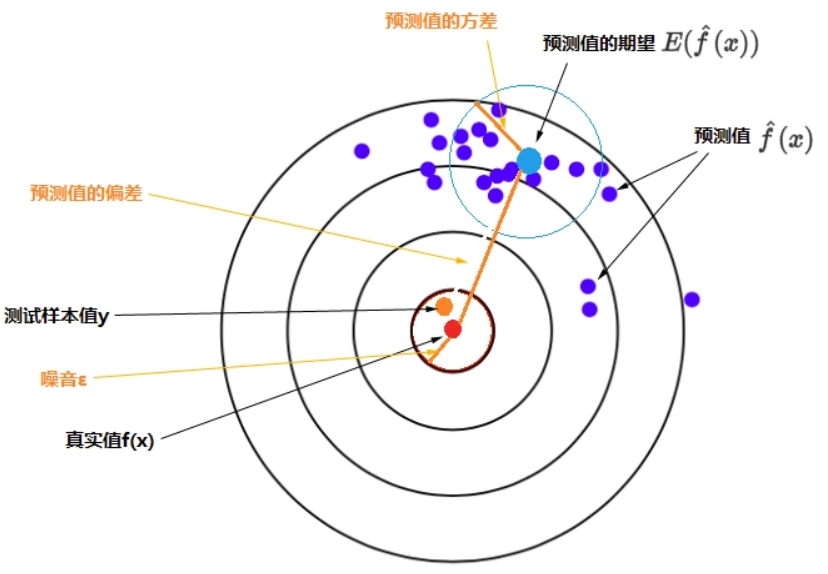
将学习到的模型中存在的误差Error分为两部分：偏差bias 和 方差variance。
在机器学习中考察 偏差 和 方差，最重要的是要在不同数据集上训练出一组特定模型，这些模型对一个测试样本进行预测，考察这一组预测值的方差和偏差。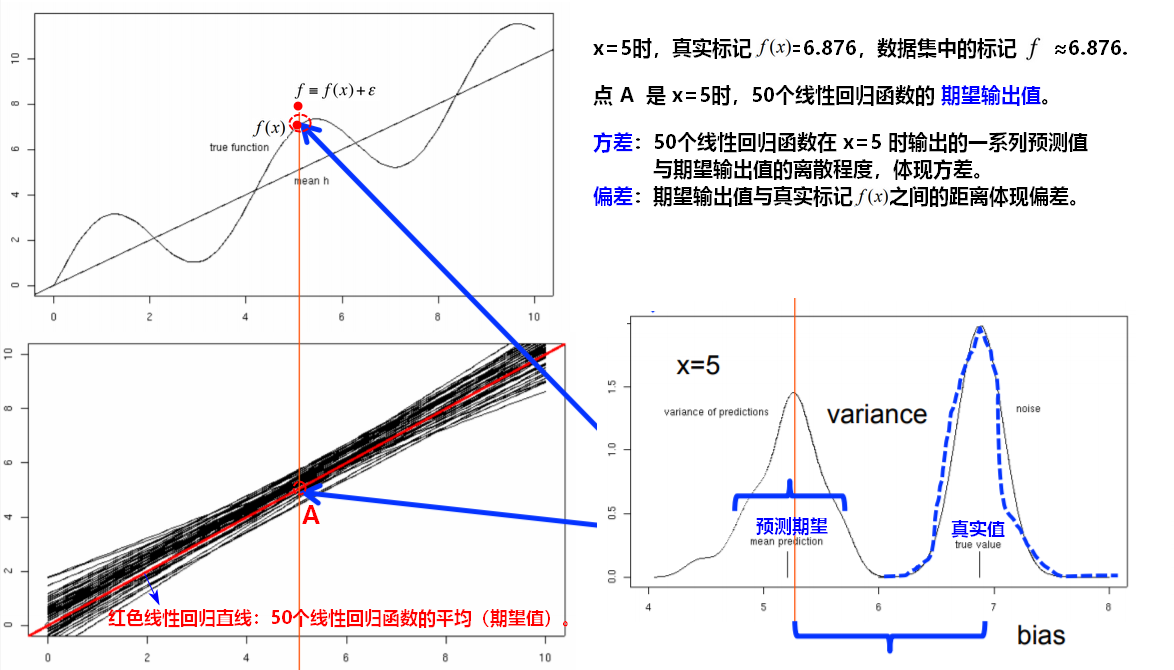

3. 偏差-方差：选择

3.1 优先顺序

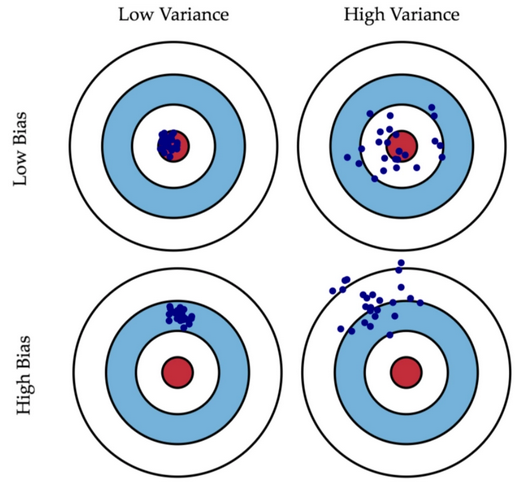
理想中，我们希望得到一个偏差和方差都很小的模型。
如图所示，
当偏差小时，各个预测值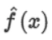集中在靶心真实值f(x)附近；
当偏差大时，各个预测值离靶心较远；
当方差小时，各个预测值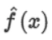集中在预测期望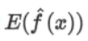附近；
当方差大时，各个预测值距离期望点分布式分散开的。

选择较好的模型时，需要使误差最小，即经验误差和泛化误差，而误差的来源是偏差和方差。选择模型时，遵循如下优先顺序：
方差小，偏差小 > 方差小，偏差大(稳定性好于后两种选择) > 方差大，偏差小 > 方差大，偏差大
“方差小，偏差大”比较稳定。很多时候实际中无法获得非常全面的数据集，那么，如果一个模型在可获得的样本上有较小的方差，说明它对不同数据集的敏感度不高，可以期望它对新数据集的预测效果比较稳定。

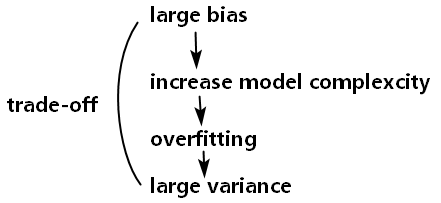
3.2 当large bias时，怎么处理？

• 在输入中加入更多特征项。
• 重新设计模型，增加模型复杂度。

复杂度高的模型，假设集合覆盖的范围更大，更有可能涵盖“真实模型”，训练模型输出的期望值和真实值之间的偏离程度更小，即偏差bias更小。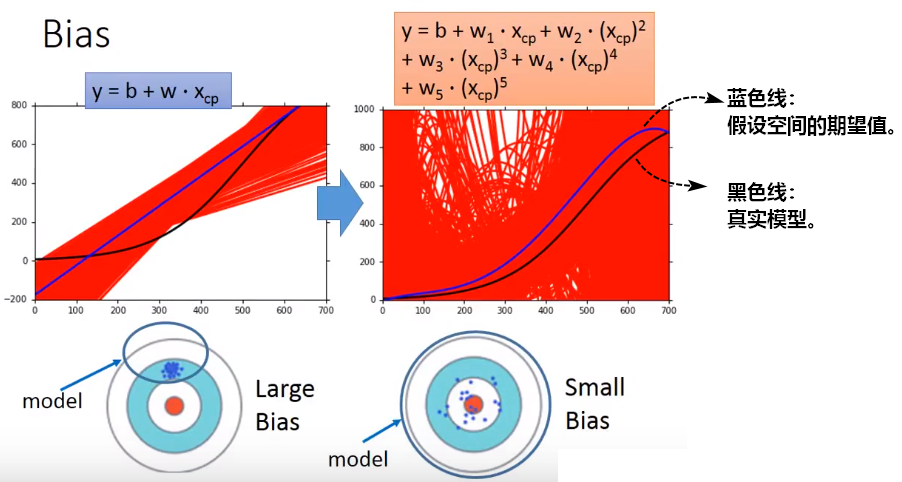

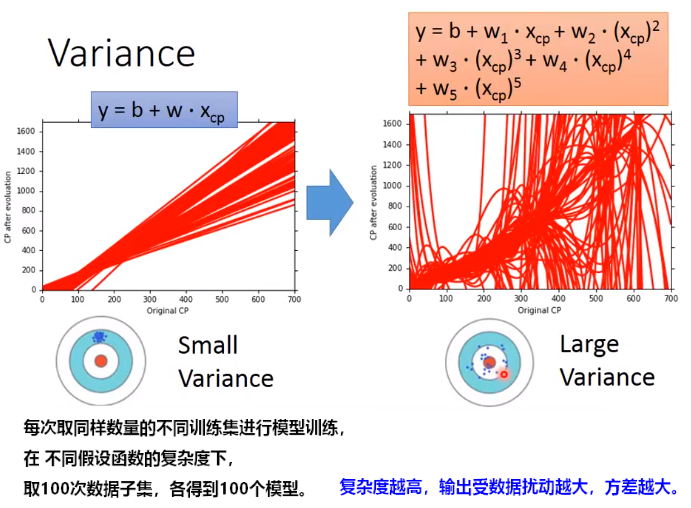
3.3 当large variance时，怎么处理？

• 增大训练数据量，丰富训练数据多样性。
• 正则化，加入惩罚项，是函数更平滑。

4. 假设集合

4.1 模型复杂度

• 越复杂的模型，假设空间的覆盖范围越大，越有可能囊括“真实模型”。

机器学习有多种算法，以及每种算法中经常又可以选择不同的结构和超参数。它们所覆盖的假设集合有不同的大小。所以，选择一种算法（包括其结构和超参数），就是选择（限定）了一个假设集合。
我们期望真实模型存在于我们所选定的假设集合范围内，并且该假设集合越小越好。

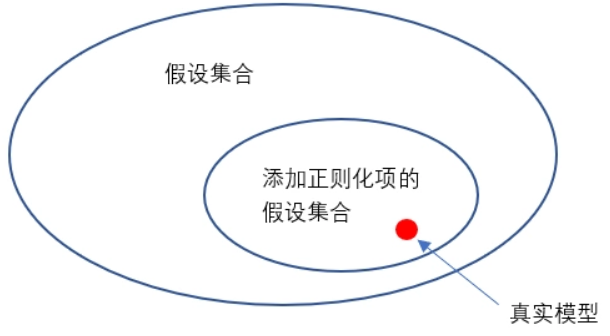
有监督学习的整个流程，其实就是一个不断缩小假设集合的过程。

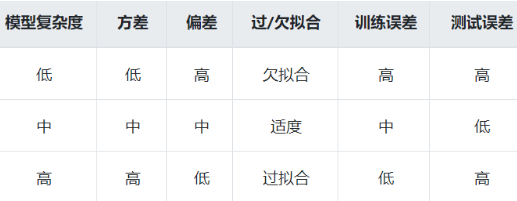
• 模型复杂度与方差、偏差的关系：

假设真实模型是一个二次多项式，那么：
线性函数集合中的模型会欠拟合（方差低，偏差太高）；
高次多项式集合中的模型容易过拟合（方差太高，偏差低）；
二项式集合中的模型能够有较好的折中（方差和偏差都相对较低），总体误差最小。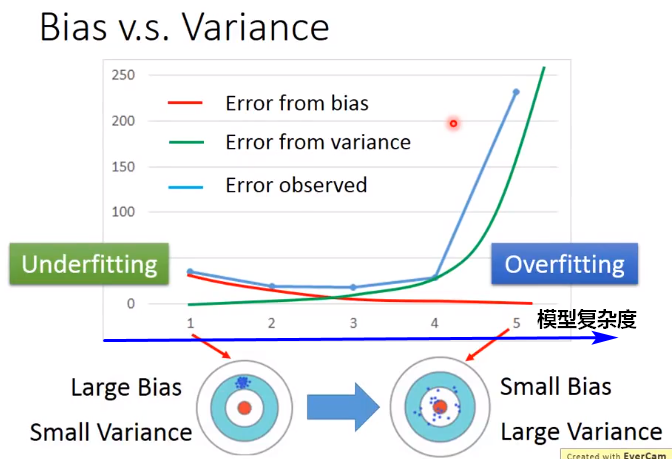

4.2 如何选择模型？

• 选择合适的假设空间（合适的模型复杂度）。
• 按照方差、偏差大小组合的优先顺序，优先选择方差小、偏差小的模型。